talks
Simon Le Cleac'h
august 16, 2022
Simon Le Cleac'h

contact is the primary mode of interaction in robotics




challenges
- not differentiable
- classical optimization methods fail
- RL has shown impressive results but
- gradient-free
- ignores dynamics model



question
how can we leverage models and gradient information to solve contact-rich robotics tasks?

- data generator for robotics optimization
differentiable physics engine


- robot's internal model of the world
- simulate contact and provide gradients
optimization problems

| control parameters | state parameters | model parameters |
|---|
decision variables
performance criteria
| optimal control |
motion synthesis | mechanism design |
| imitation learning | state estimation | system identification |
| movement costs |
|---|
| model-data mismatch |
Emo Todorov, Optico: A Framework for Model-Based Optimization with MuJoCo Physics, NeurIPS 2019
optimization as an oracle

- trajectory optimization with privileged information
- can generate a lot of 'expert demonstrations' for a learning algorithm

- useful gradient information
differentiable physics engine
- stable and accurate simulation

contact physics

LCP
implicit complementarity
gradients
samples
subgradient
existing physics engines
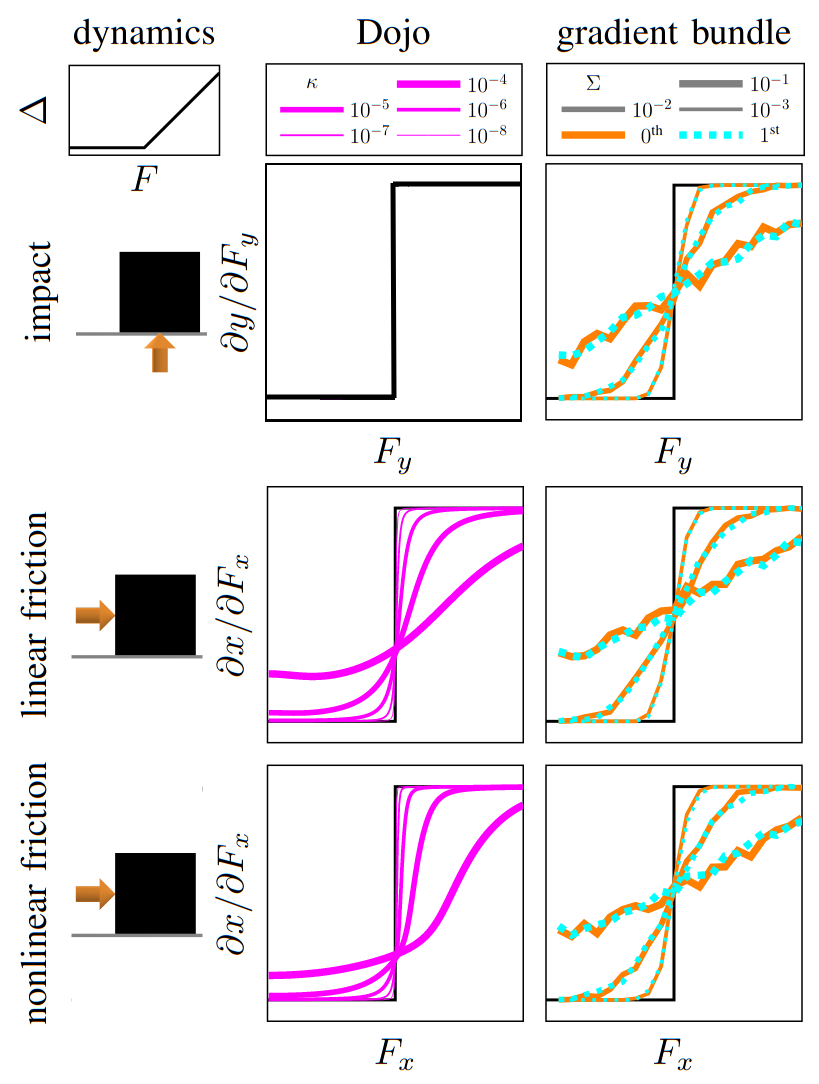

Dojo key ideas
stability at low rates
variational integrator
interior-point methods
accurate contact dynamics
implicit differentiation
smooth gradients



Discrete mechanics and variational integrators. J. E. Marsden and M. West.
discretize
discretize
Euler-Lagrange
Euler-Lagrange


variational integrator
variational integrator
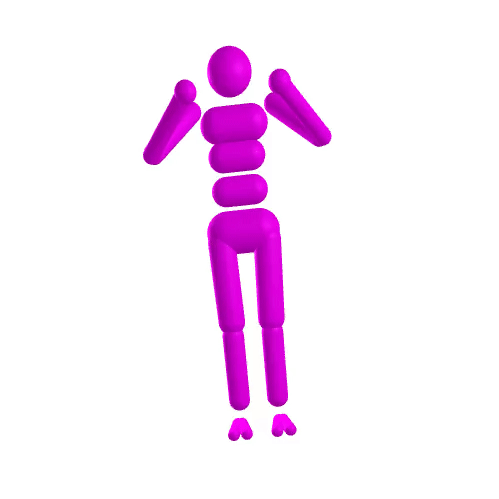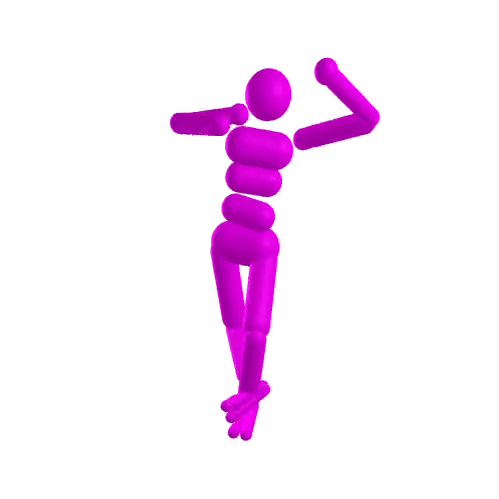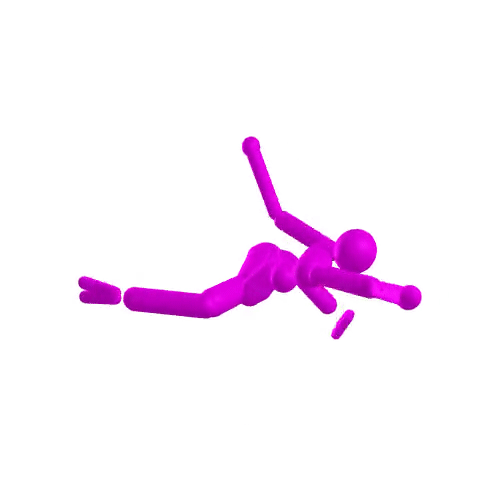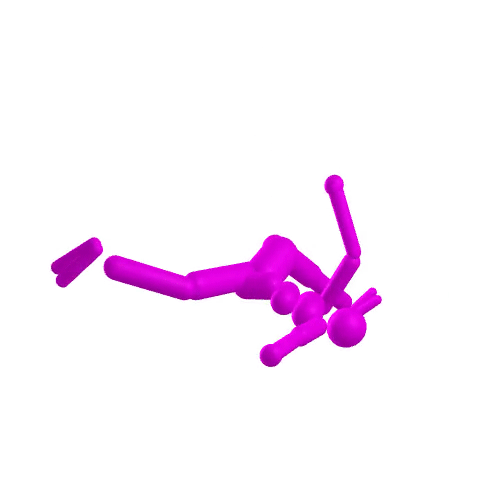
-
compare astronaut energy and momentum conservation to MuJoCo

- Dojo performs orders of magnitude better
- stability at low rates
accurate contact dynamics


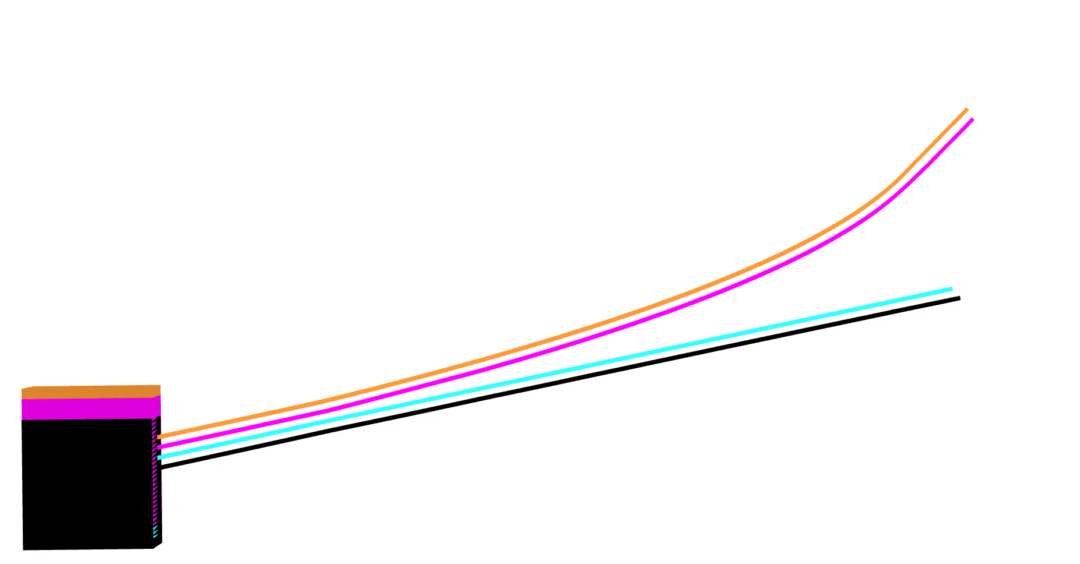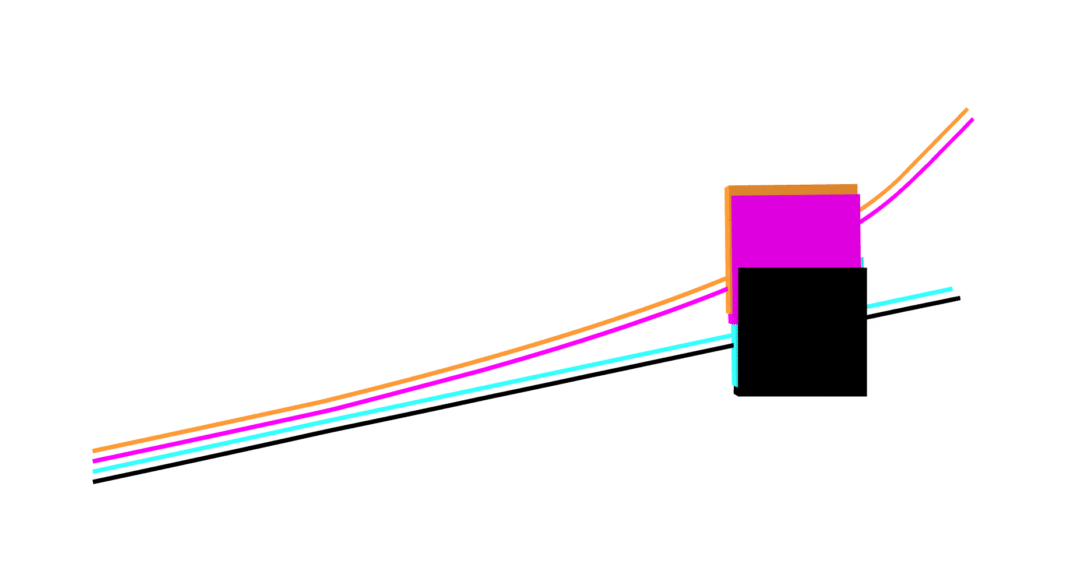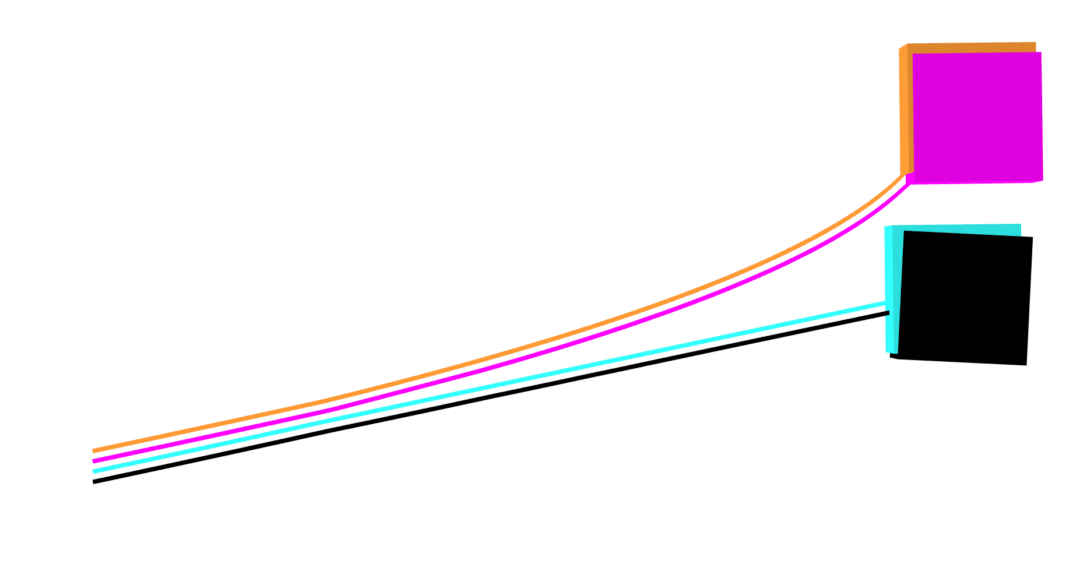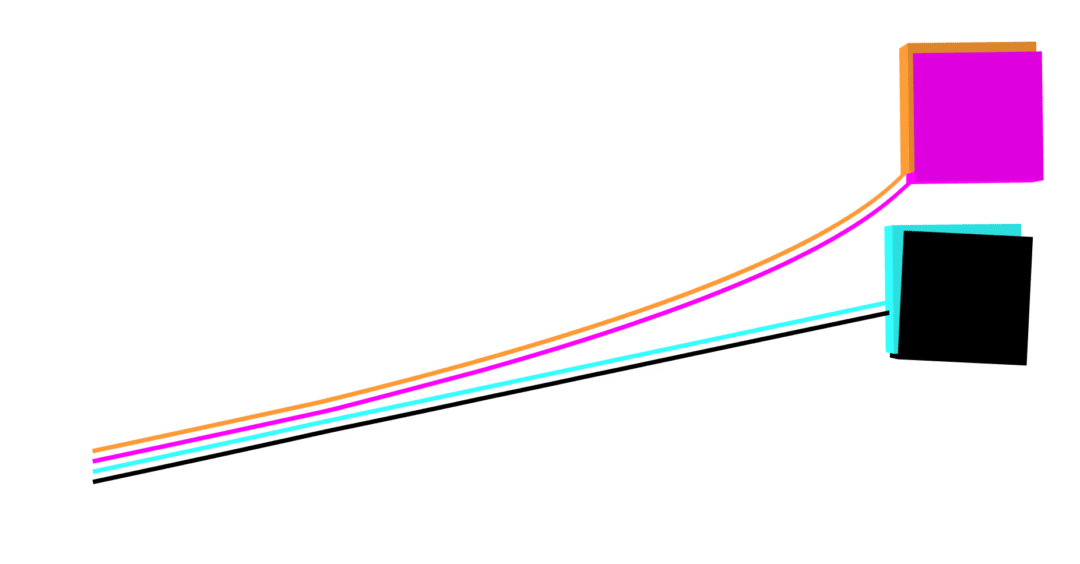
MuJoCo linear
Dojo linear
MuJoCo nonlinear
Dojo nonlinear
no collision violations
correct Coulomb friction
interior-point method
impact → inequalities
friction → second-order cone
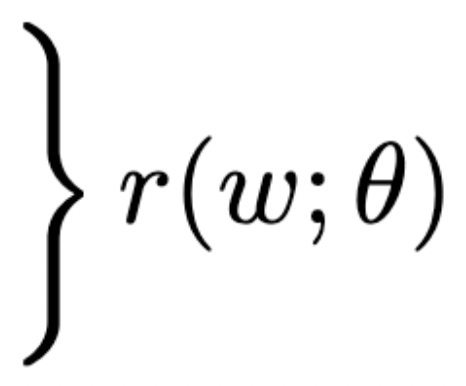
cone constraints

custom interior-point solver
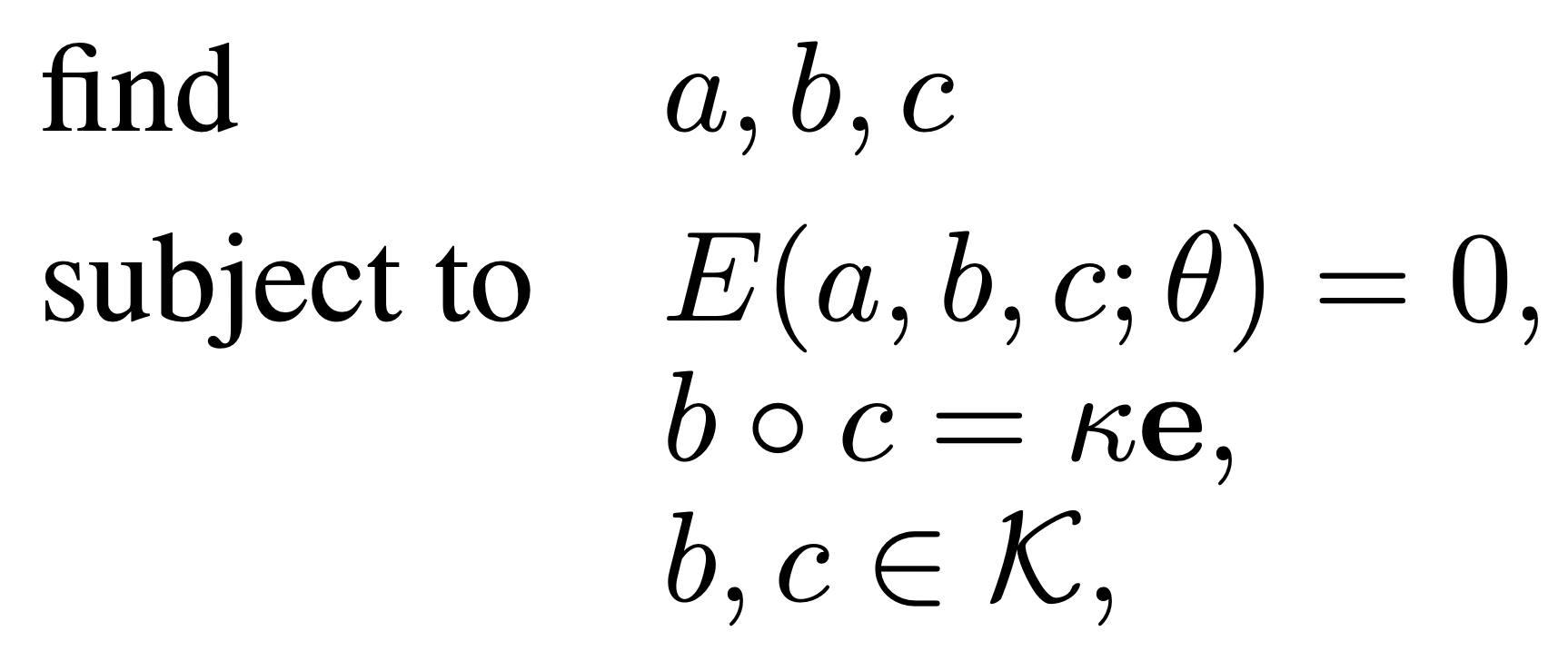
- Mehrotra predictor-corrector algorithm
- CVXOpt second-order cones
- non-Euclidean support for quaternions
accurate contact dynamics

nonlinear complementarity problem
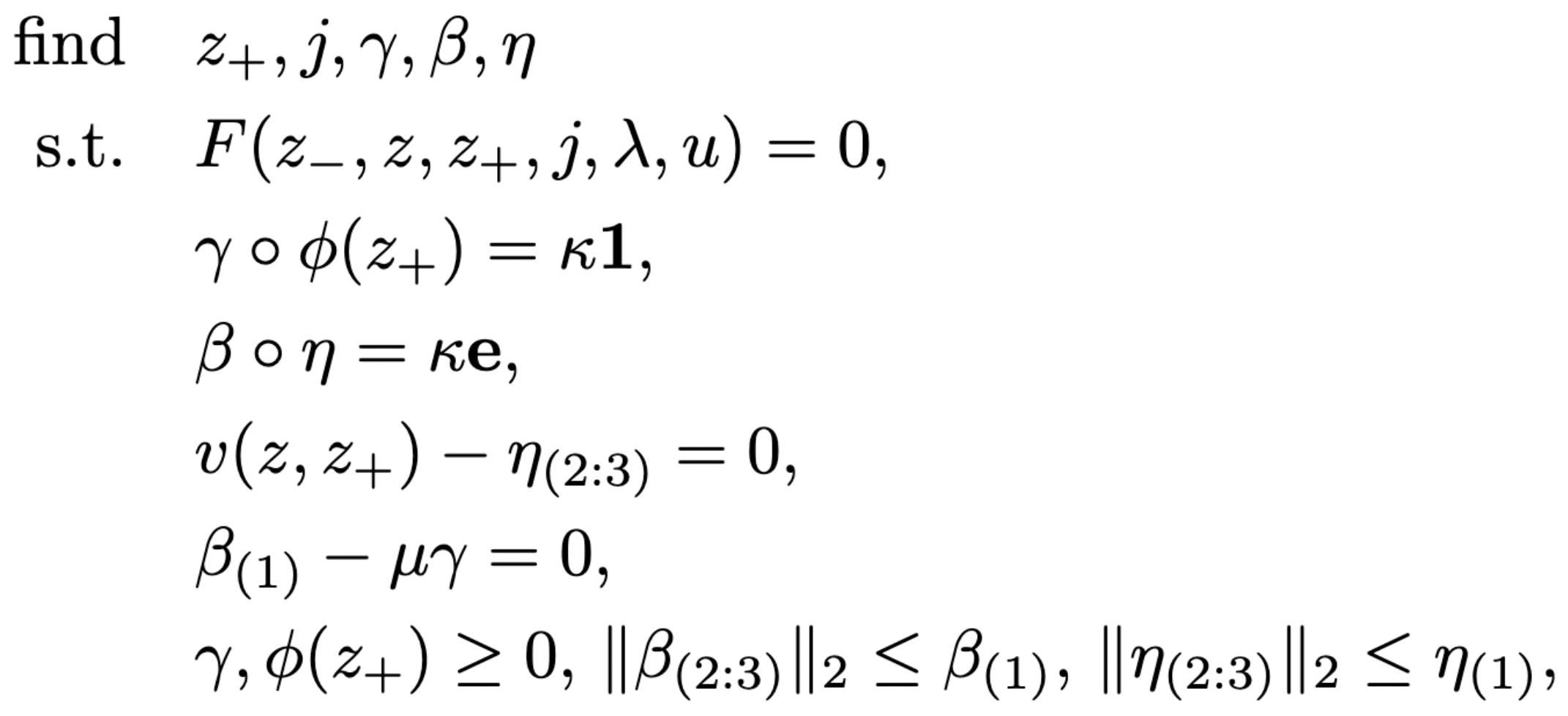
accurate contact dynamics

custom interior-point solver
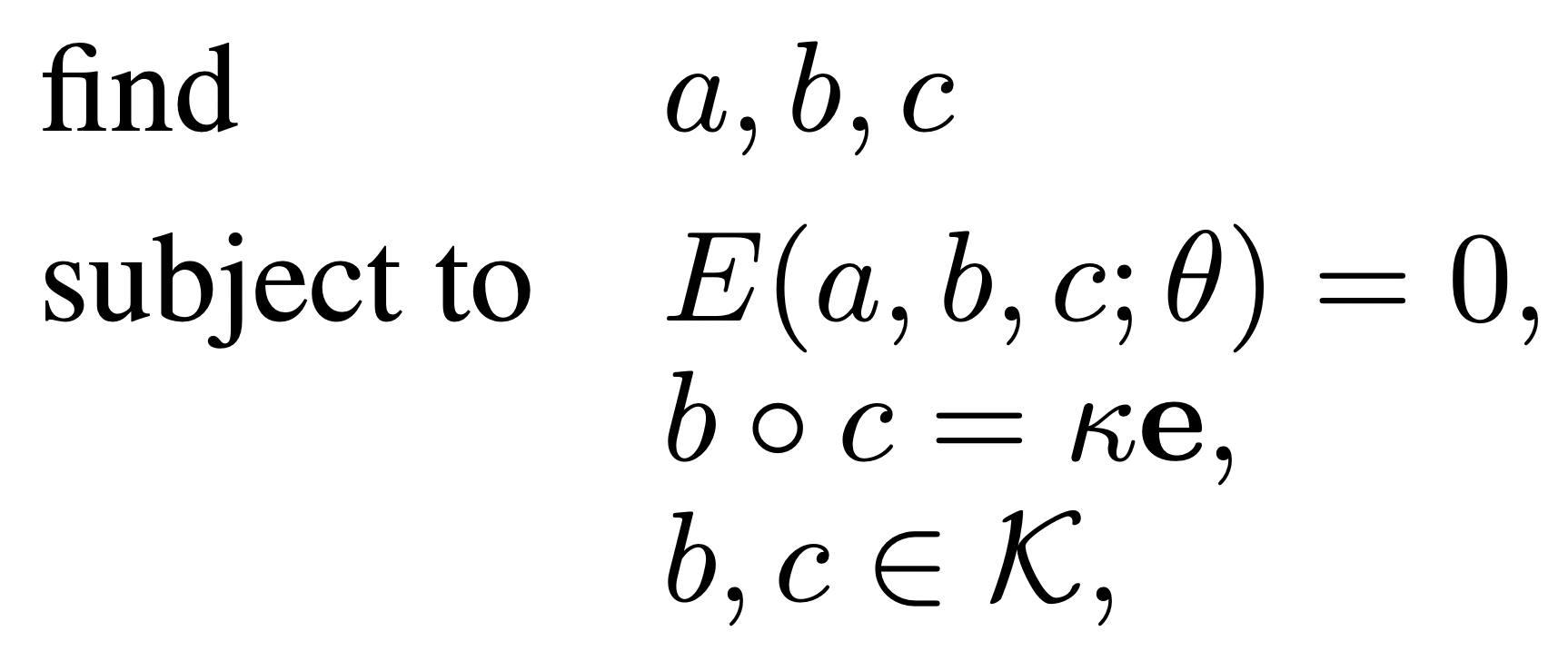
accurate contact dynamics
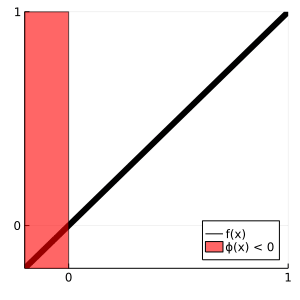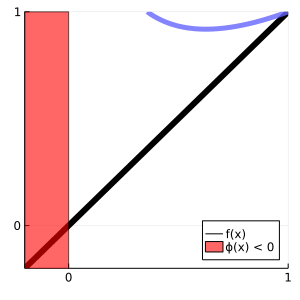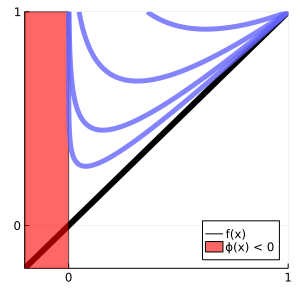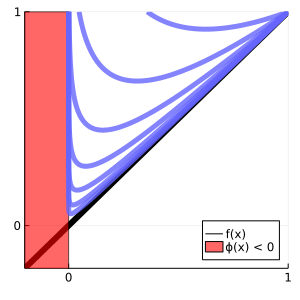




embedding learned models

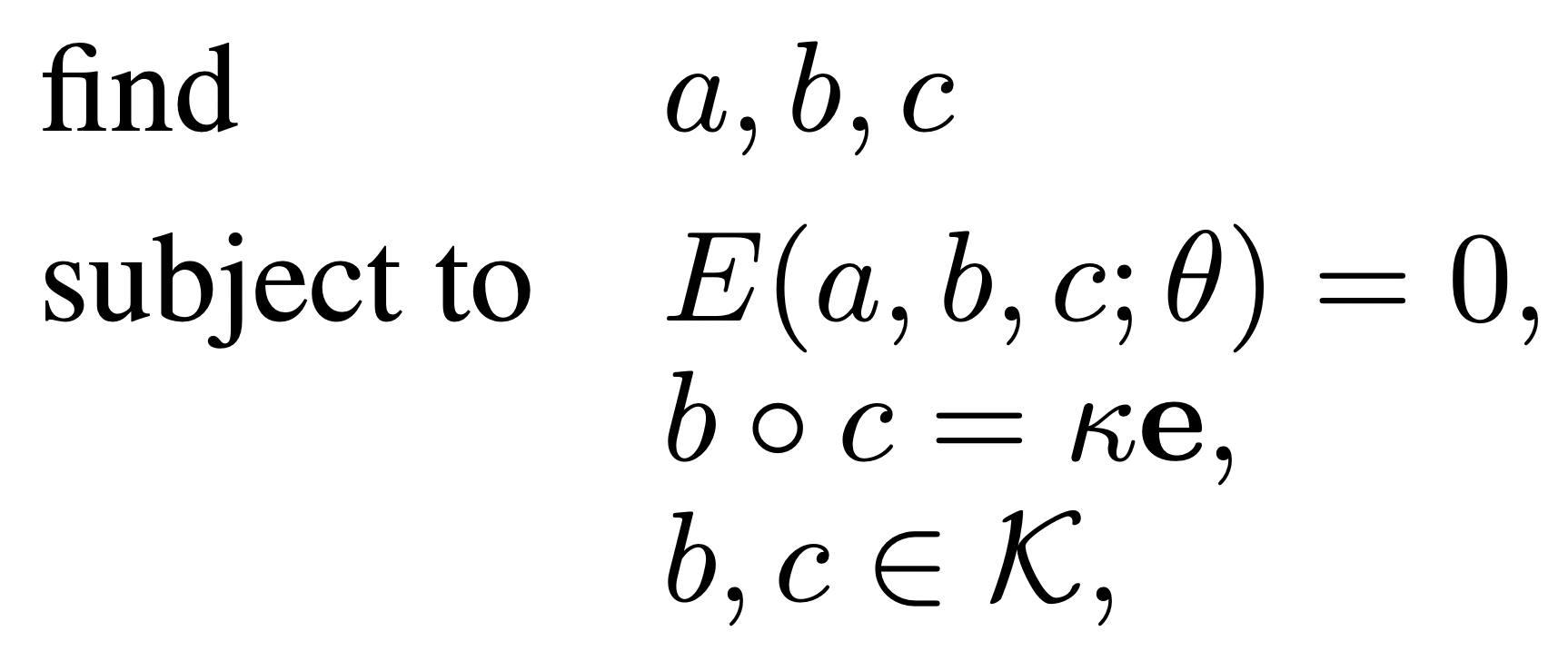
physics
physics
robot
environment
object
learned

→
smooth gradients
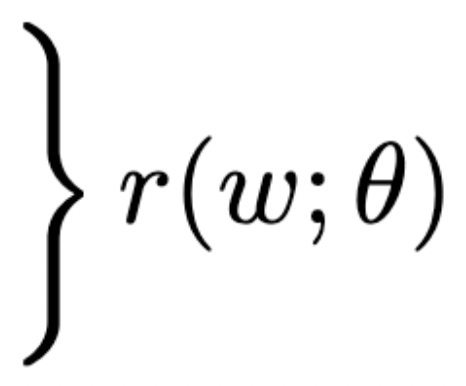
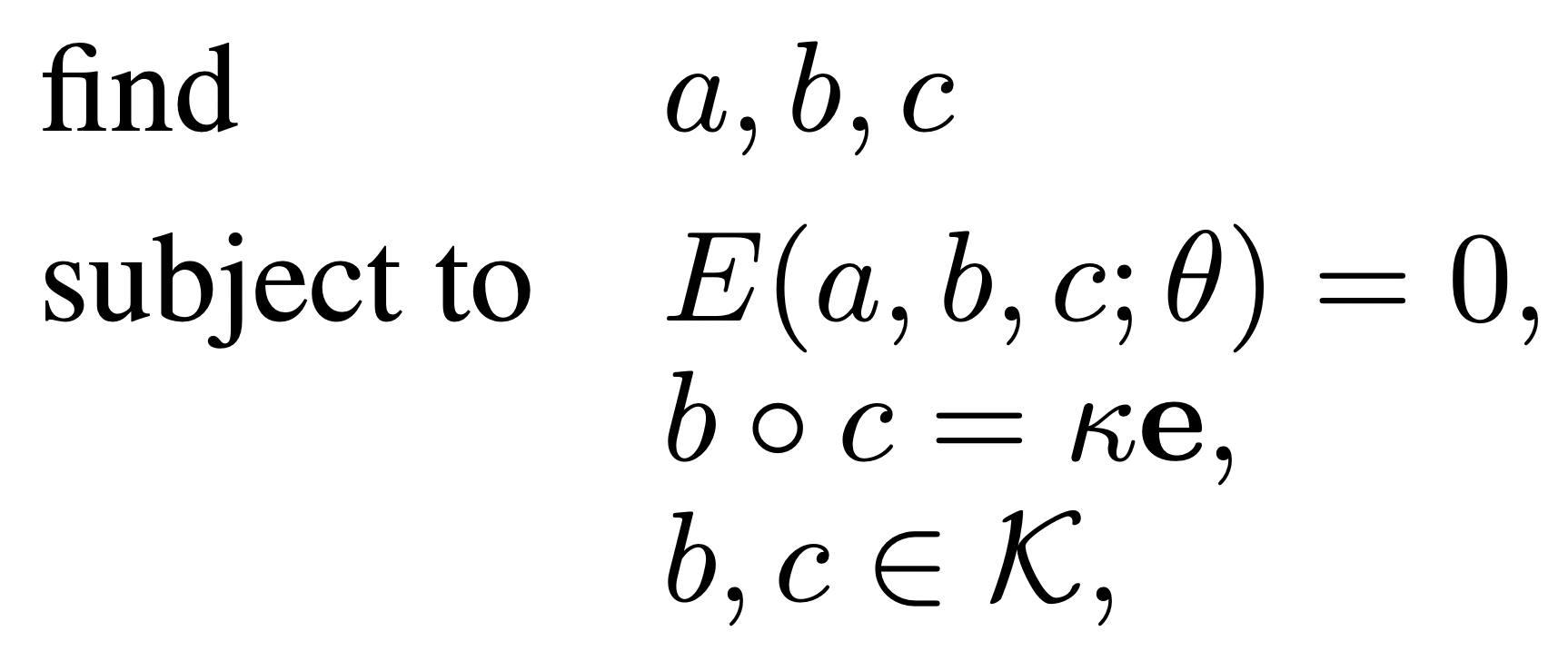
residual
solution
parameters
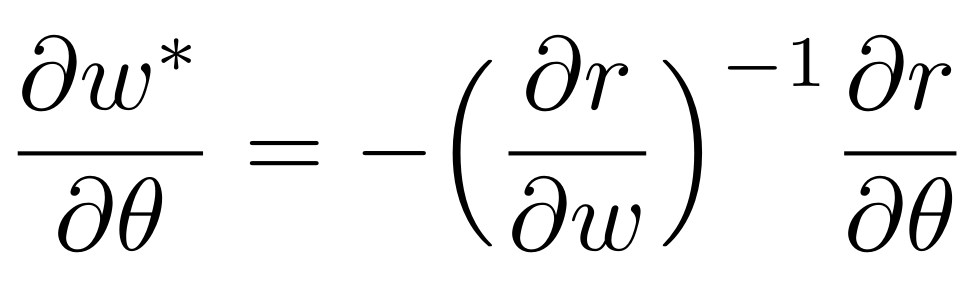
sensitivity of solution w.r.t problem data

computation cost of gradient is less than simulation step
smooth gradients
Lezioni di analisi infinitesimale. U. Dini.
Dojo gradients vs sampling

less expensive to compute compared to finite-difference or stochastic sampling
randomized smoothing
finite difference
Dojo
matrix backward substitution
matrix factorization
matrix factorization
Dojo's gradient vs MuJoCo's finite difference



box push
non-smooth dynamics
gradient comparison
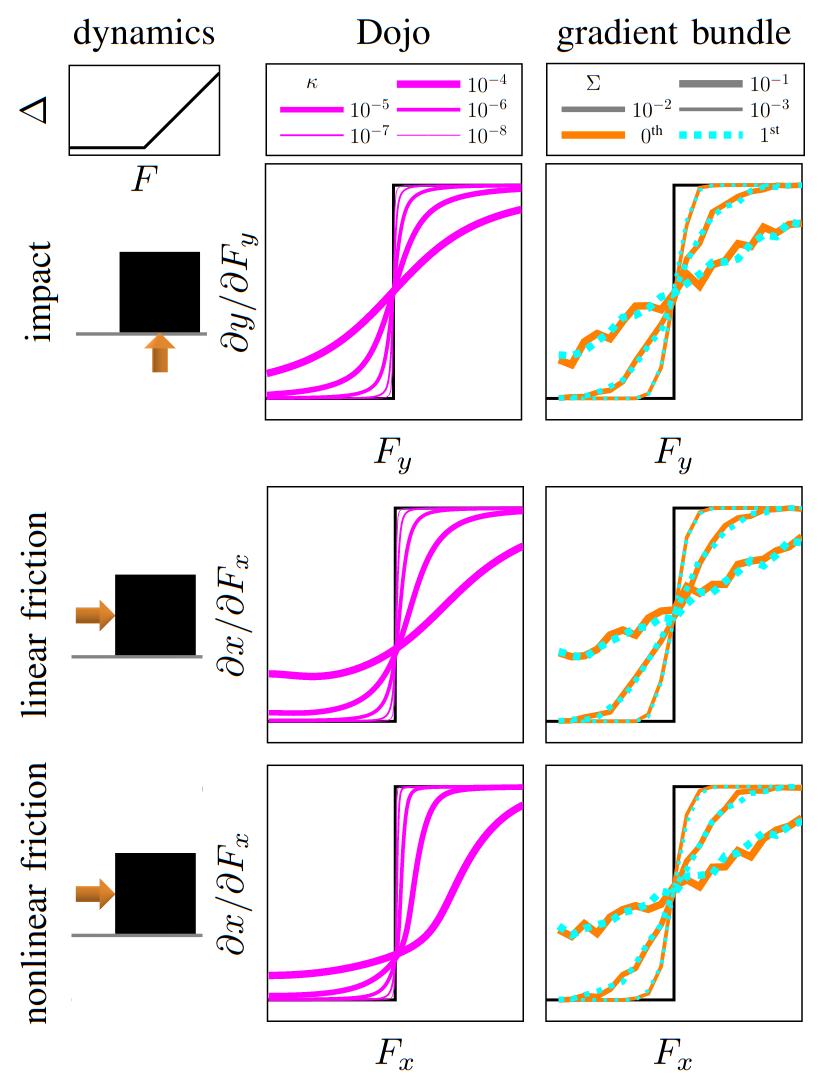
Dojo
randomized smoothing
differentiate intermediate barrier problems for smooth gradients
Dojo gradients vs sampling
examples

trajectory optimization

smooth-gradient-based optimization with iterative LQR



stability at low rates enables 2-5x sample-complexity improvement over MuJoCo
reinforcement learning


train static linear policies for locomotion

gradients enable 5-10x sample-complexity improvement over derivative-free method
stability at low rates enables 2-5x sample-complexity improvement over MuJoCo
system identification
ContactNets: Learning Discontinuous Contact Dynamics with Smooth, Implicit Representations. S. Pfrommer, M. Halm, and M. Posa.
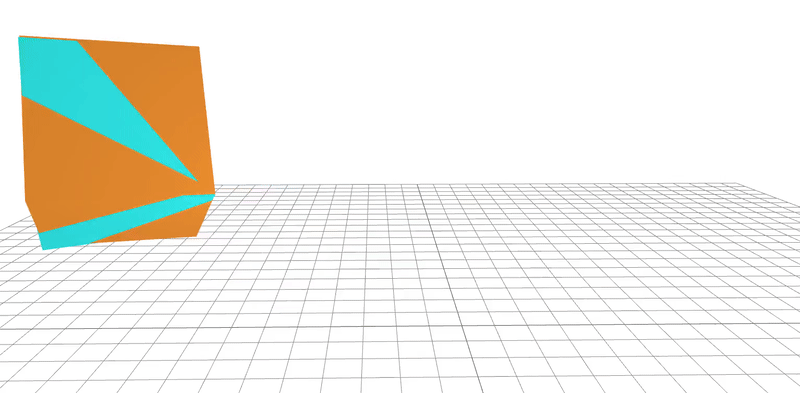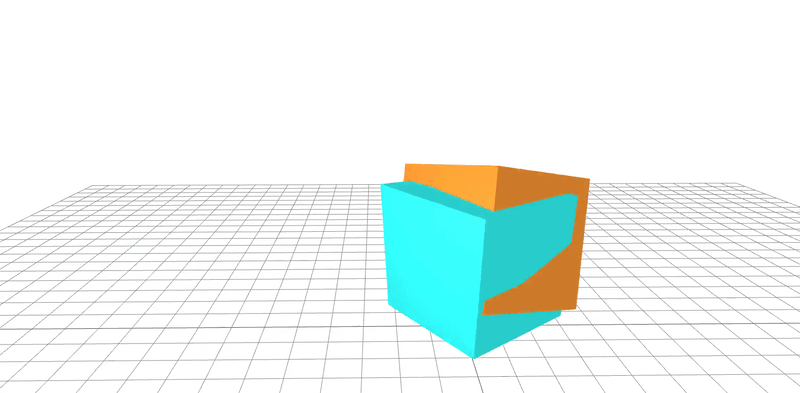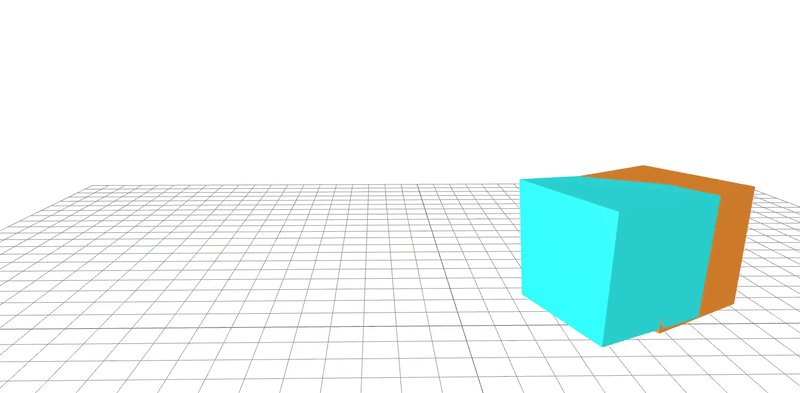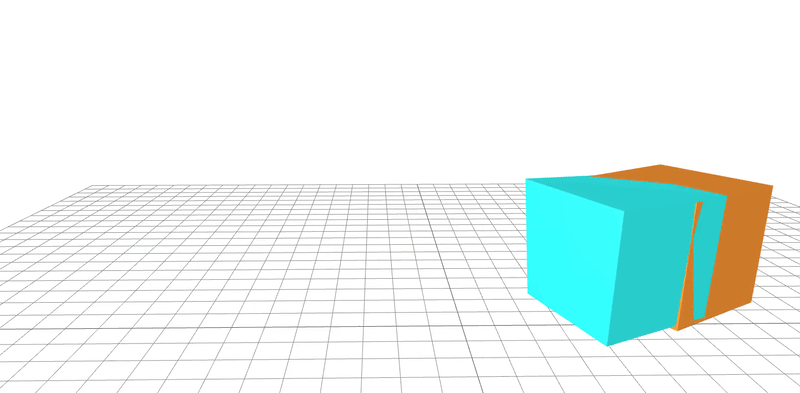
learned
ground-truth


real-word dataset
Dojo environment
system identification

geometry
friction coefficient
ground-truth
learned

Quasi-Newton method utilizes gradients to
learn parameters to 95% accuracy in 20 steps
model-predictive control


Fast Contact-Implicit Model-Predictive Control.
S. Le Cleac'h & T. Howell, C. Lee, S. Yang, M. Schwager, Z. Manchester


simulation
push recovery
behavior generation
running policy at 200-500Hz
related work

Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasi-dynamic Contact Models, Tao Pang∗, H.J. Terry Suh∗, Lujie Yang and Russ Tedrake,
RRT using the same smoothed derivatives as Dojo
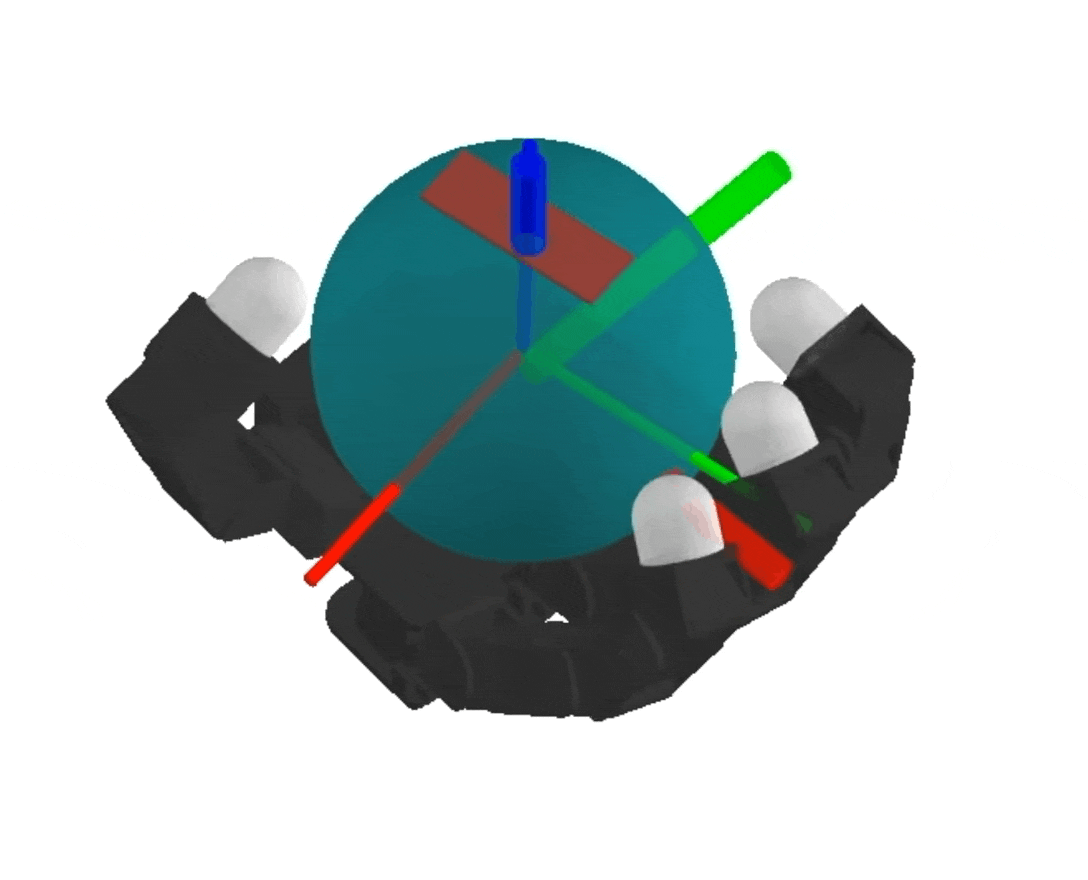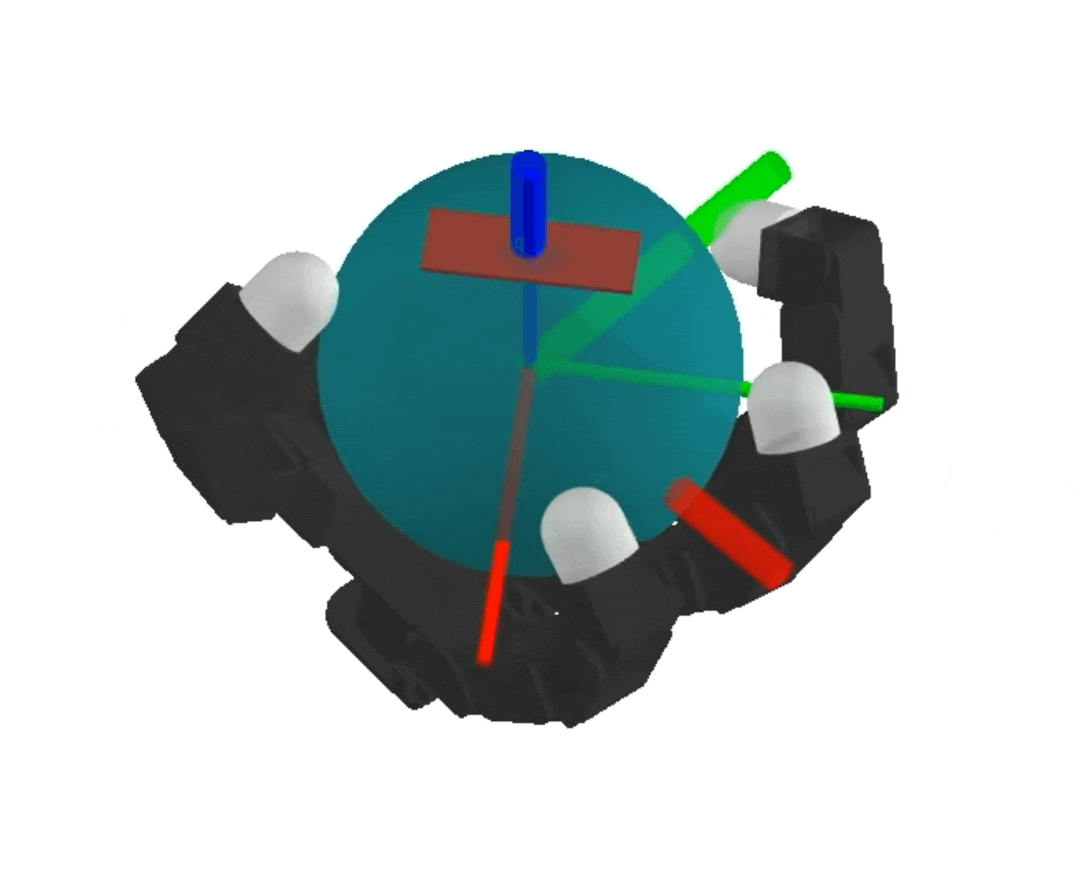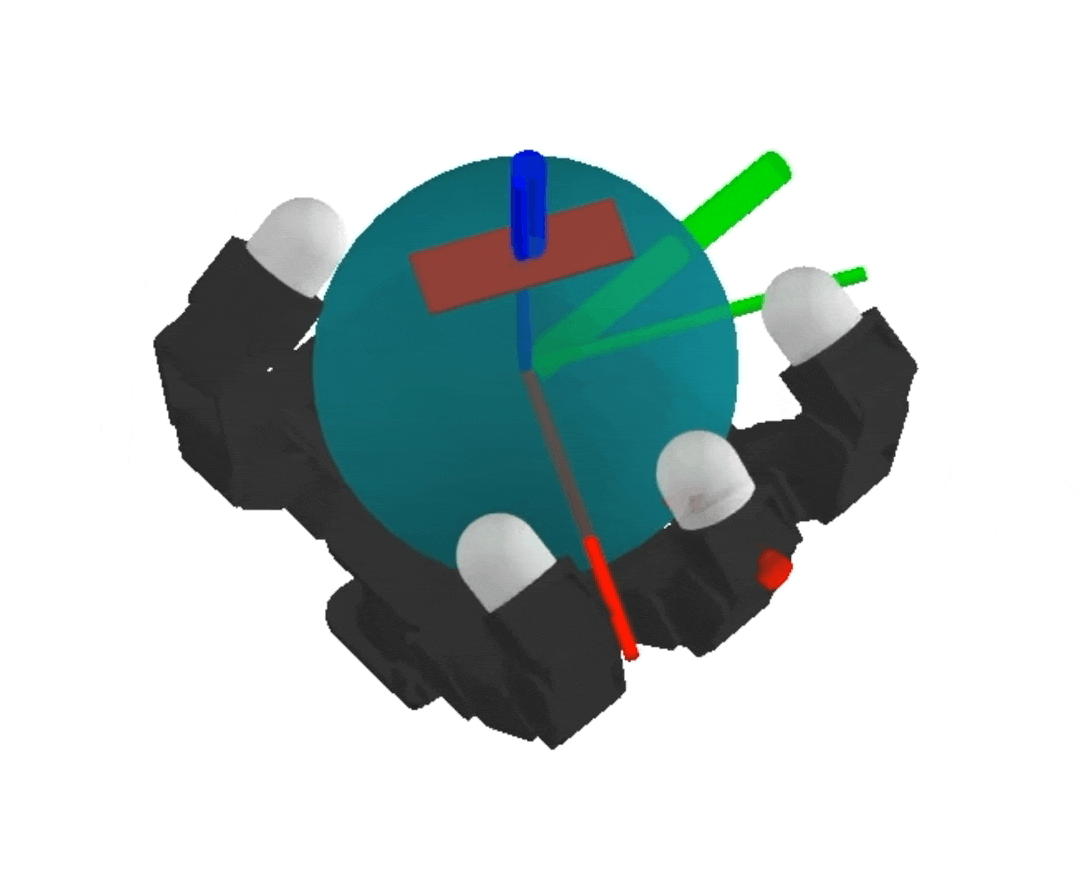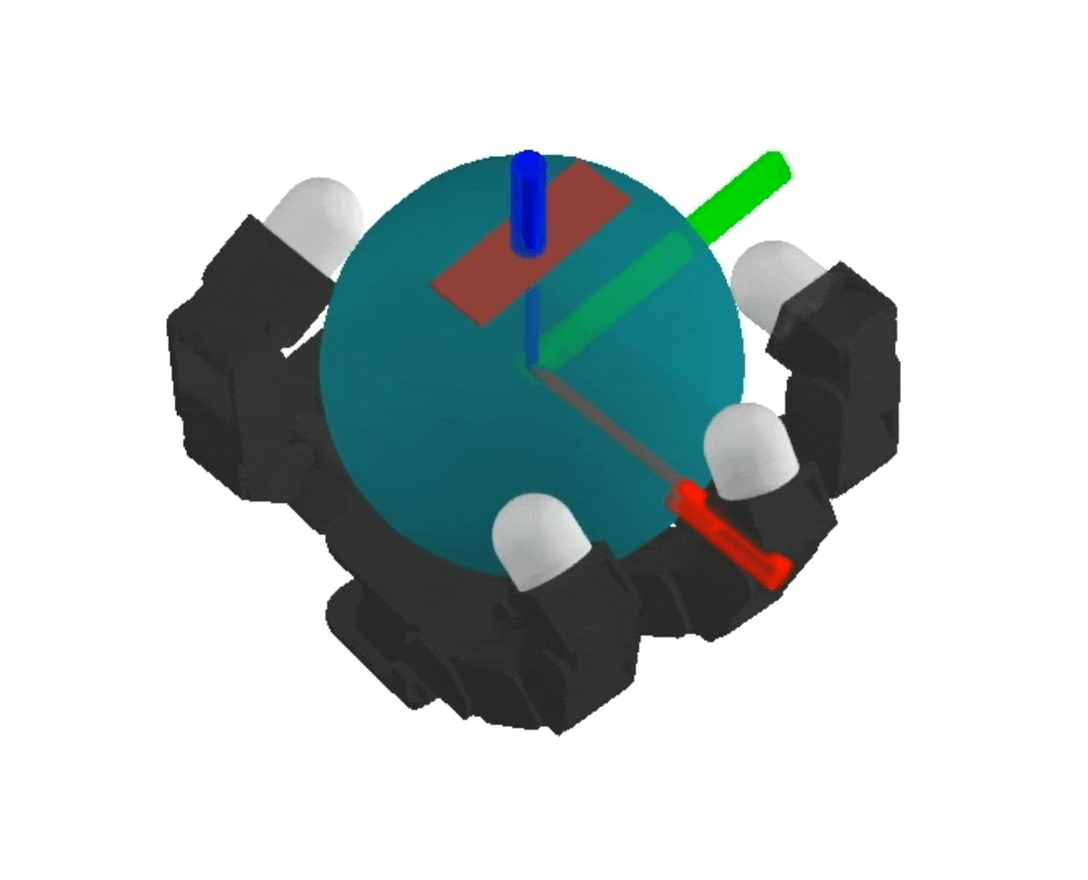
NeRF

Differentiable Physics Simulation of Dynamics-Augmented Neural Objects. S. Le Cleac'h, HX. Yu, M. Guo, T. Howell, R. Gao, J. Wu, Z. Manchester, M. Schwager
dynamics-augmented NeRF → complex collision geometries

optimization problems

| control parameters | state parameters | model parameters |
|---|
decision variables
performance criteria
| optimal control |
motion synthesis | mechanism design |
| imitation learning | state estimation | system identification |
| movement costs |
|---|
| model-data mismatch |
Emo Todorov, Optico: A Framework for Model-Based Optimization with MuJoCo Physics, NeurIPS 2019
differentiable optimization modules


differentiable simulator

online optimization-based policy
(MPC, etc.)
control inputs
gradients
gradients

offline optimization
(RL, RRT, etc.)
motion plans
trajectories
optimization as a differentiable module

- build fast robust and differentiable optimization tools:
- sysID
- motion generation
- optimal control
- state estimation
- etc.
- can act as layers or differentiable modules in a larger control struture
- MPC autotuning
- MPC with neural networks bits






Taylor Howell
Simon Le Cleac'h
Jan Brüdigam
Zico Kolter
Mac Schwager
Zachary Manchester
team



Shuo Yang
Chi Yen Lee

Sumeet Singh
Simon Le Cleac'h
Pete Florence


hierarchical implicit representation for manipulation planning
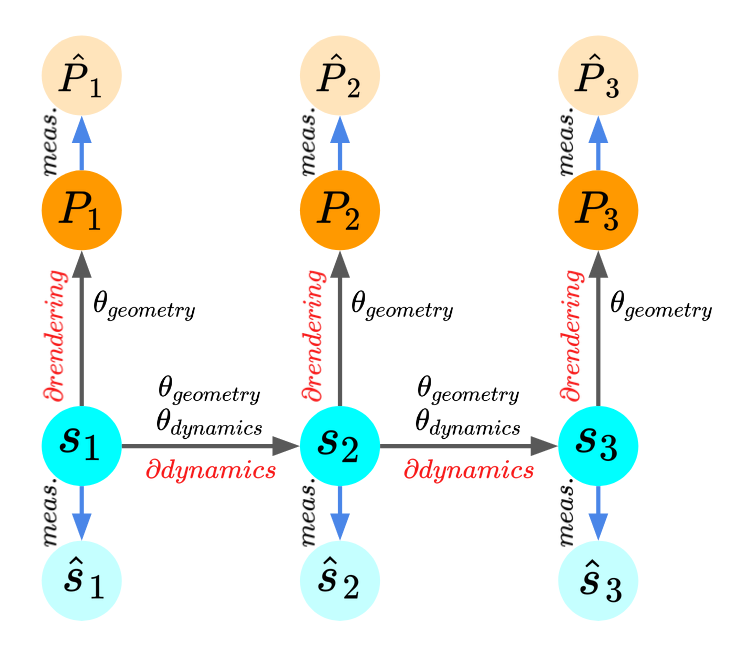
differentiable
simulation
sensor data
point cloud data
noisy pose measurements
geometry, friction, mass, etc.
learned dynamics representation
hierarchical implicit representation for manipulation planning
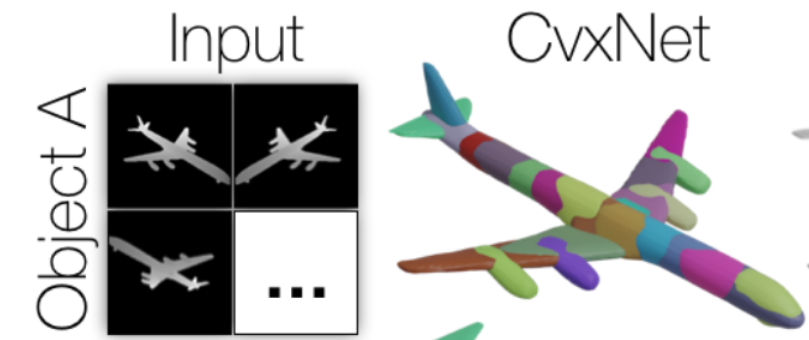

hierarchical implicit representation for manipulation planning
hierarchical implicit representation for manipulation planning

differentiable
dynamics
differentiable
point cloud
hierarchical implicit representation for manipulation planning
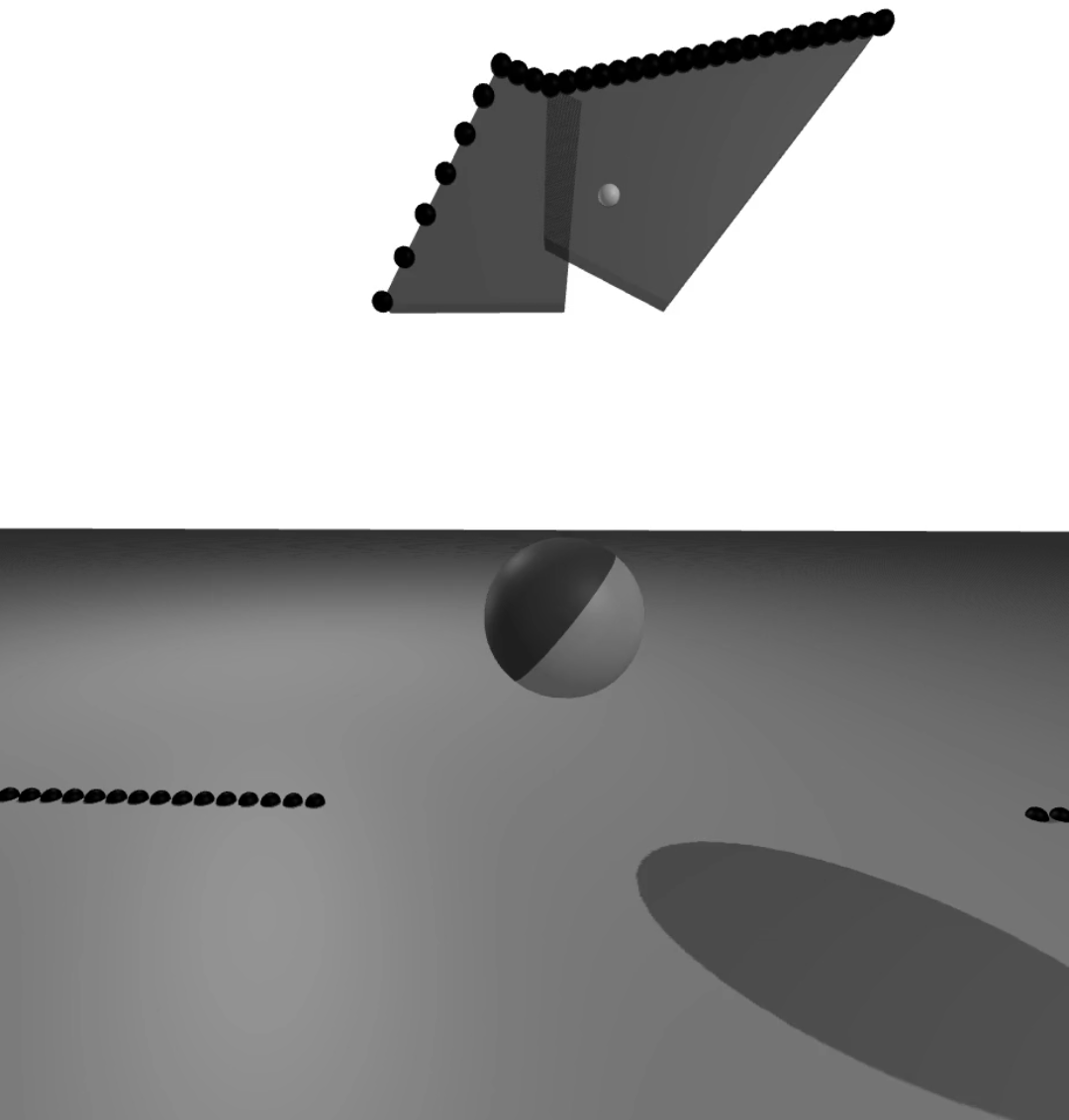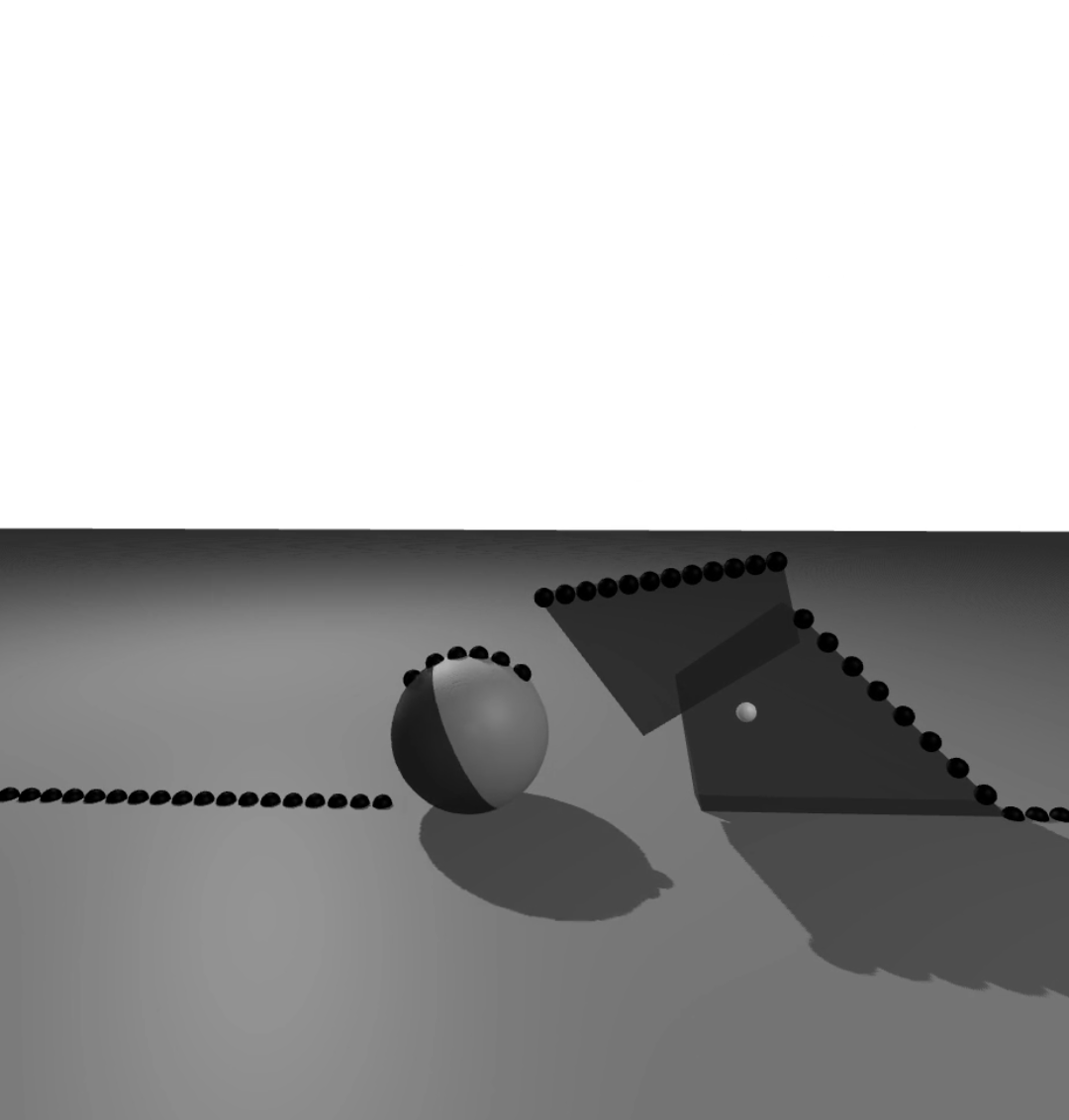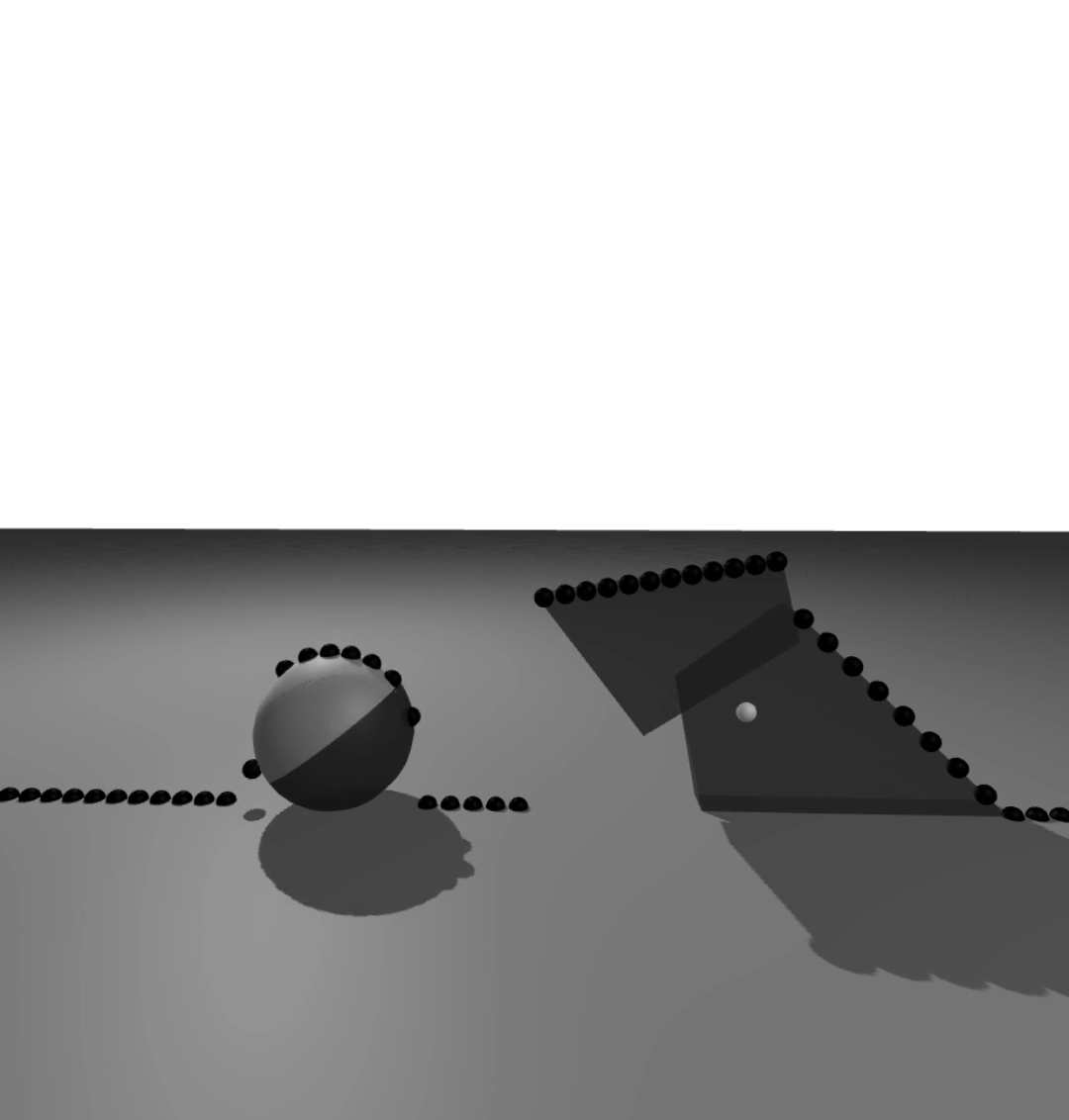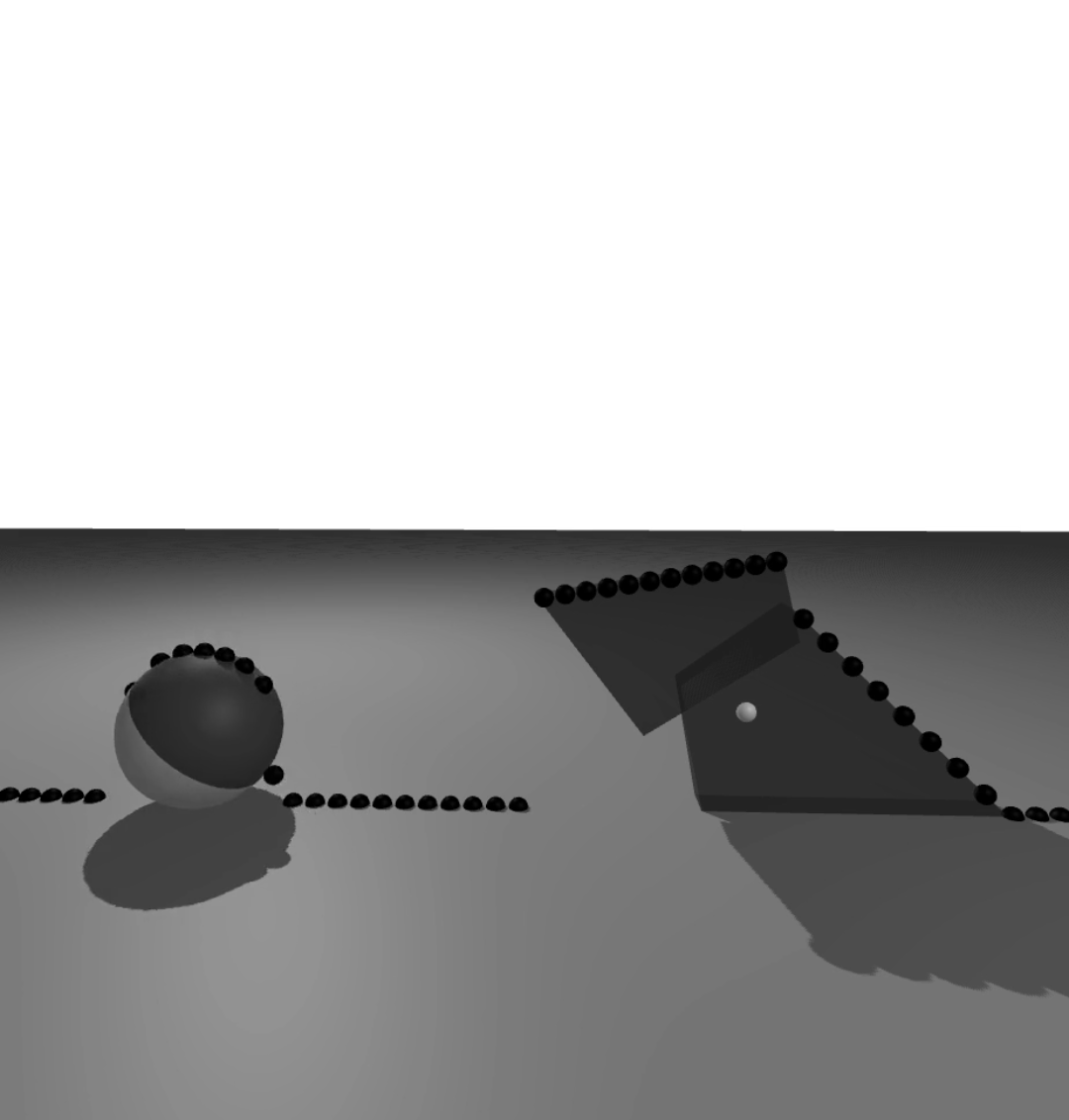
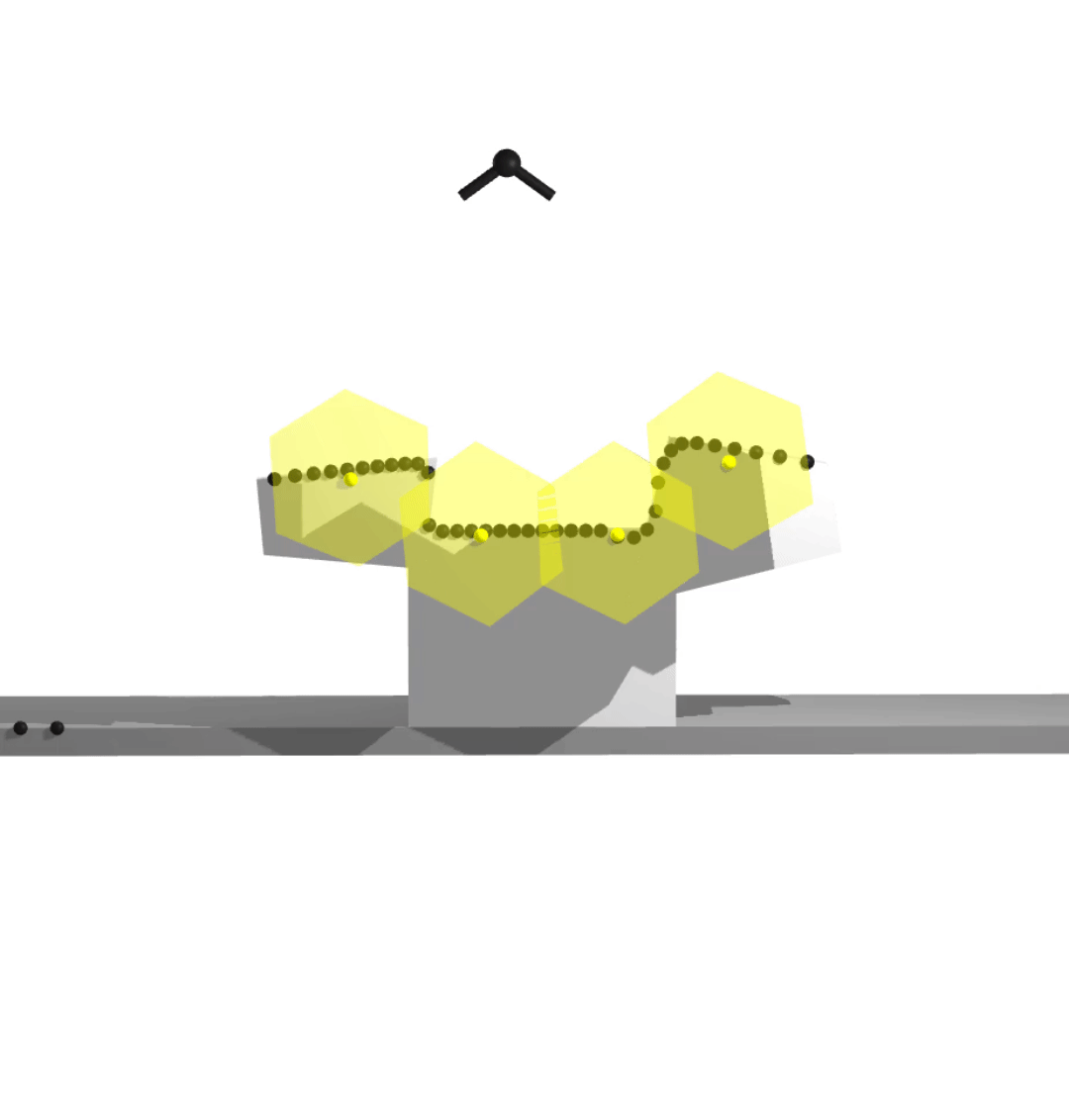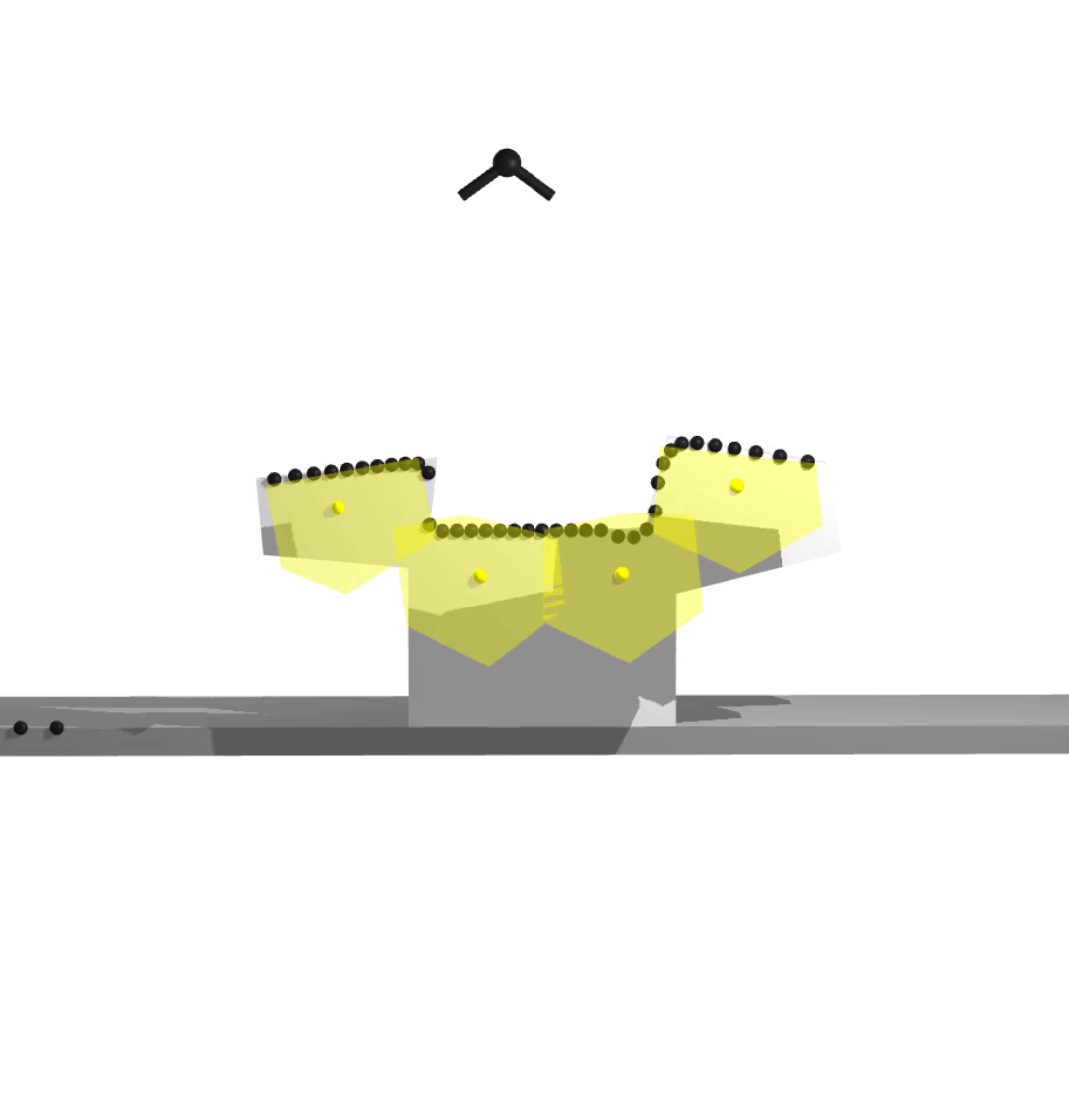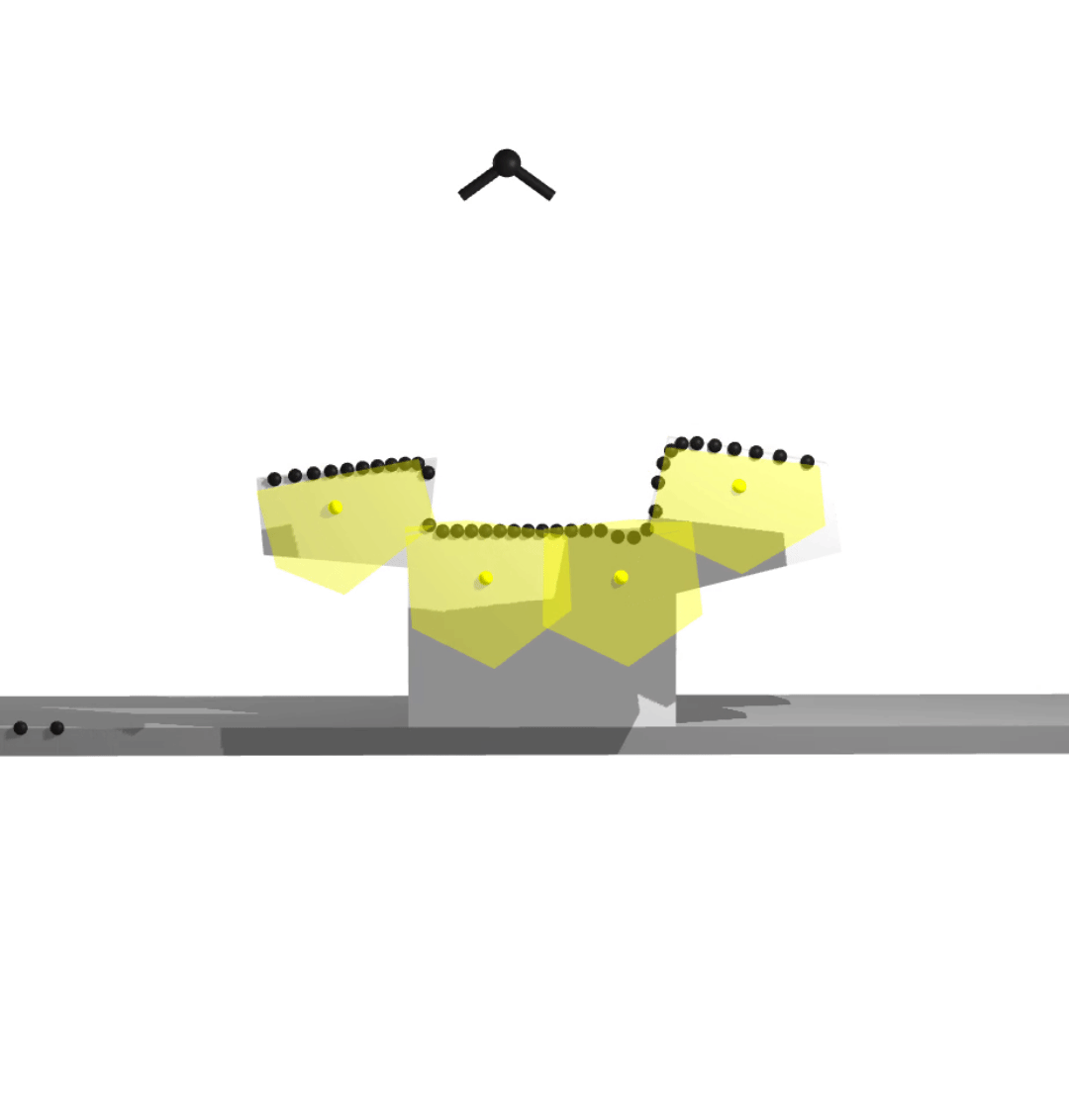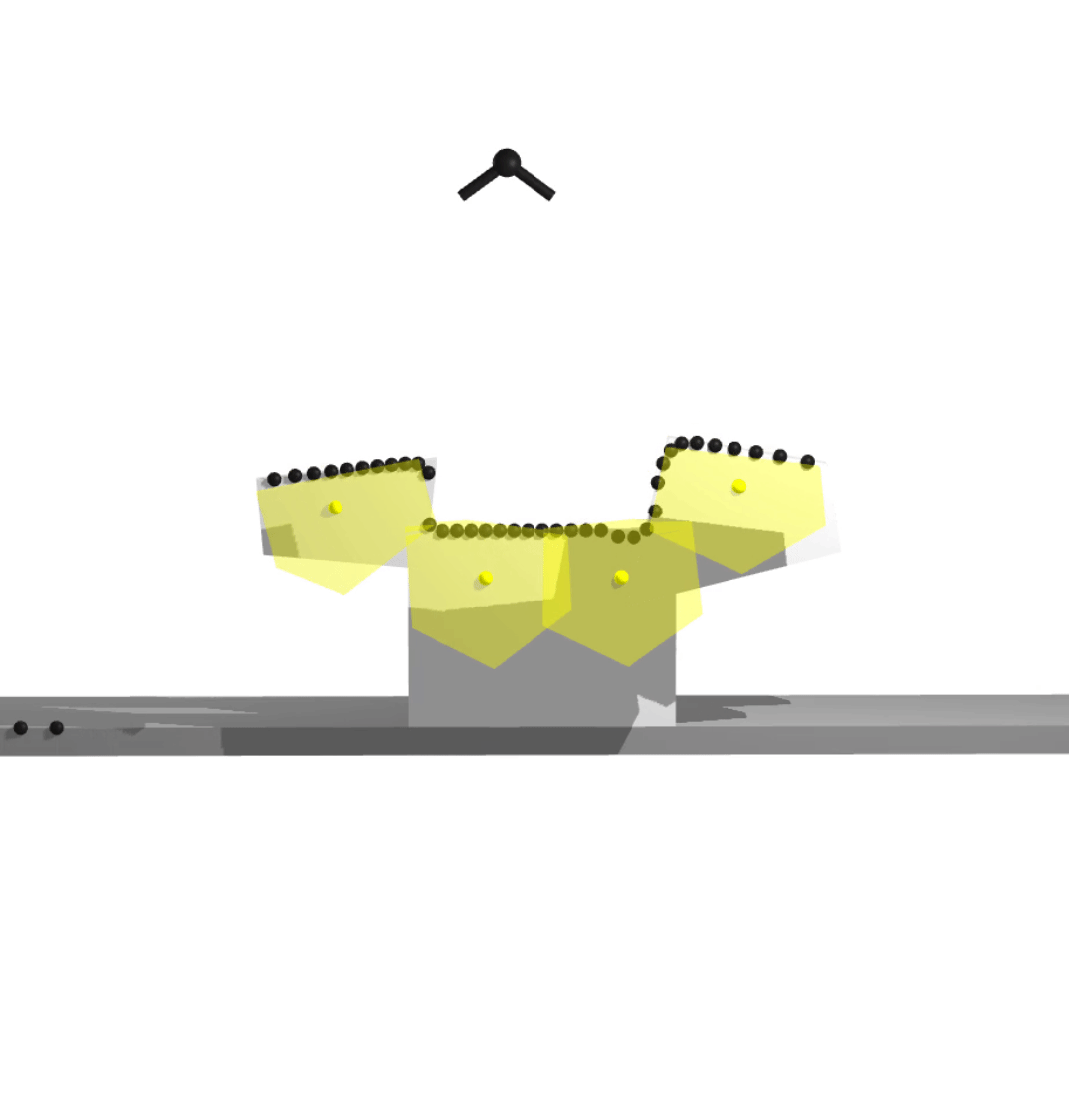
hierarchical implicit representation for manipulation planning

Sumeet Singh
Simon Le Cleac'h
Pete Florence


hierarchical implicit representation for manipulation planning
SBPL group
august 10, 2022
Simon Le Cleac'h
a differentiable physics engine for robotics
Simon Le Cleac'h and Taylor Howell




Taylor Howell
Simon Le Cleac'h
team

thowell@stanford.edu
simonlc@stanford.edu
contact physics

LCP
implicit complementarity
gradients
samples
subgradient
existing physics engines




Dojo key ideas
stability at low rates
variational integrator
interior-point methods
accurate contact dynamics
implicit differentiation
smooth gradients




Discrete mechanics and variational integrators. J. E. Marsden and M. West.
discretize
discretize
Euler-Lagrange
Euler-Lagrange


variational integrator
variational integrator
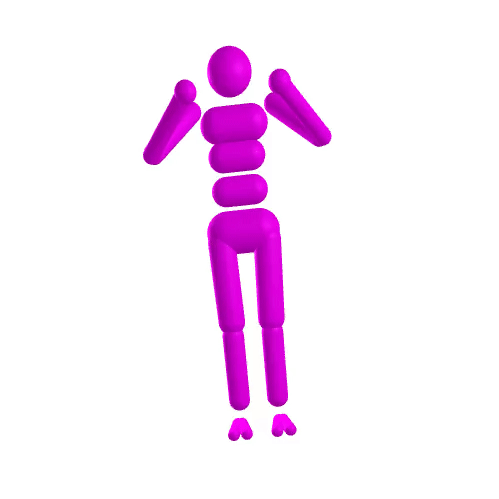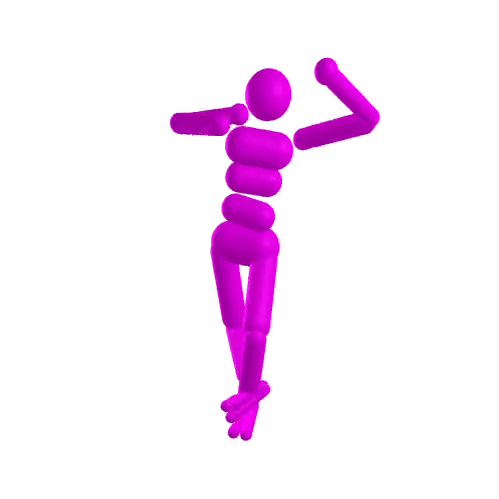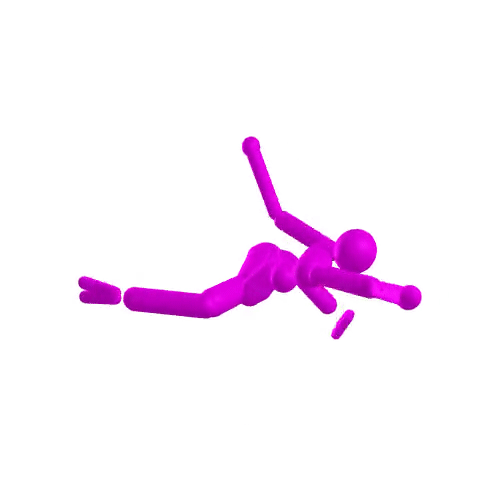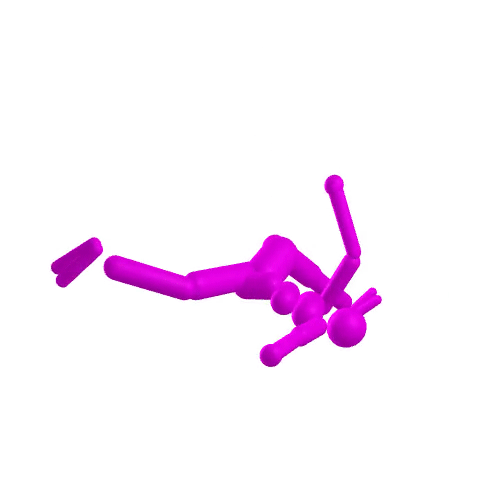
-
compare astronaut energy and momentum conservation to MuJoCo

- Dojo performs orders of magnitude better
- stability at low rates
accurate contact dynamics


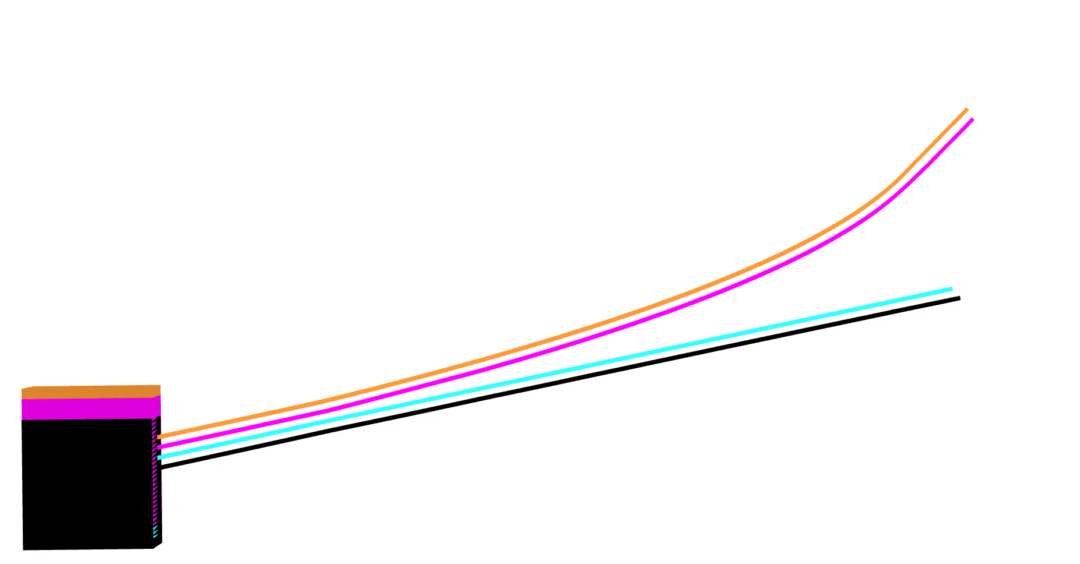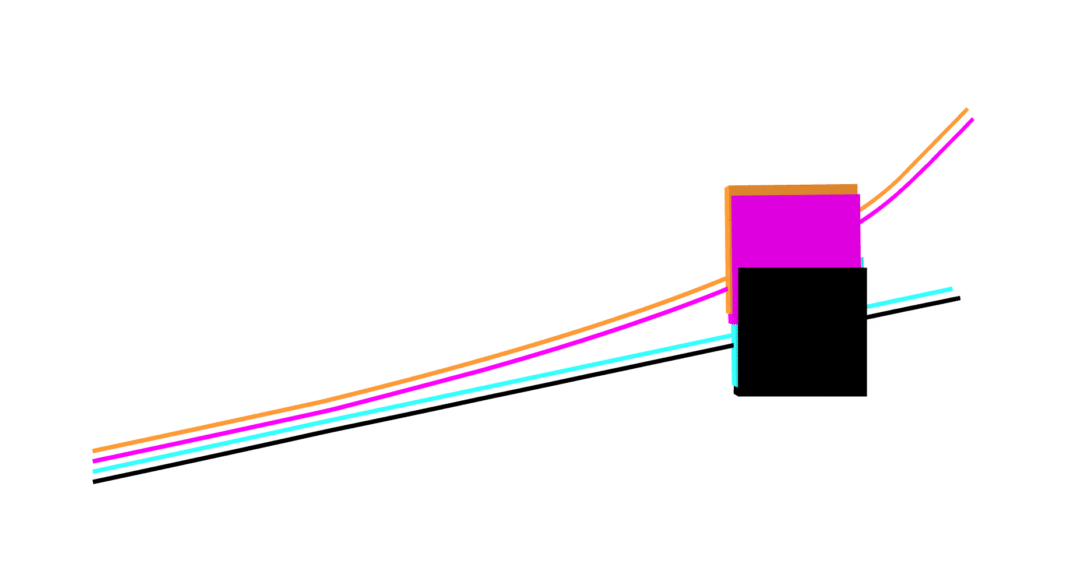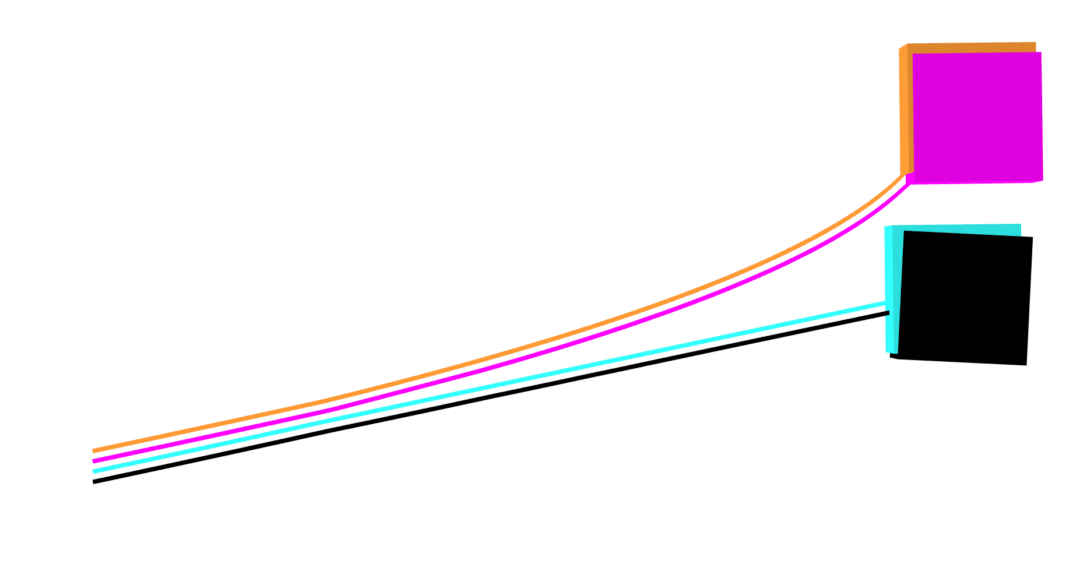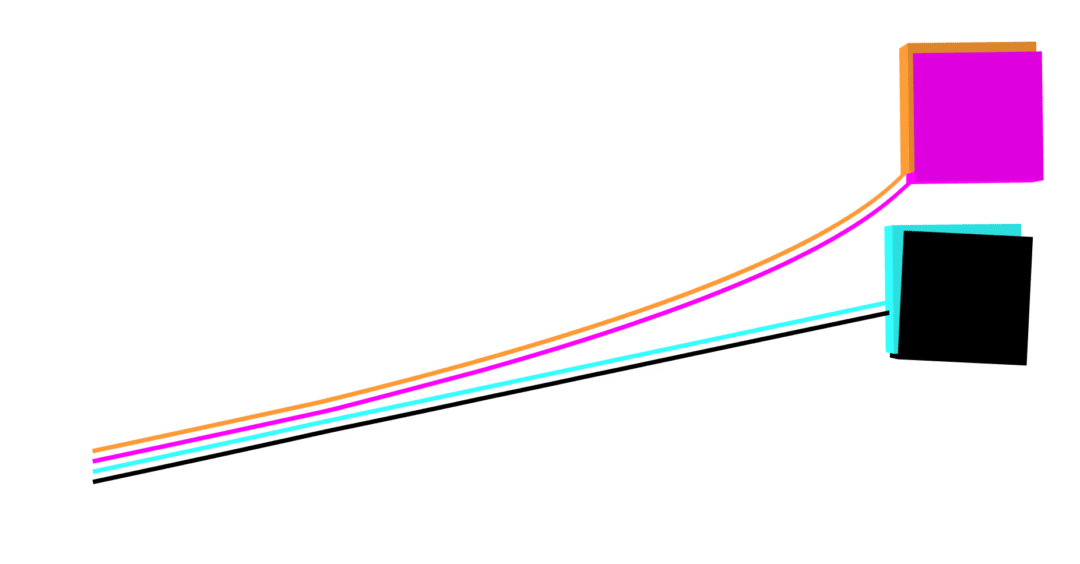
MuJoCo linear
Dojo linear
MuJoCo nonlinear
Dojo nonlinear
no collision violations
correct Coulomb friction
interior-point method
impact → inequalities
friction → second-order cone
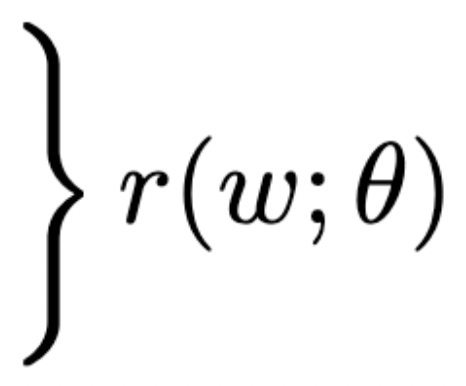
cone constraints

nonlinear complementarity problem
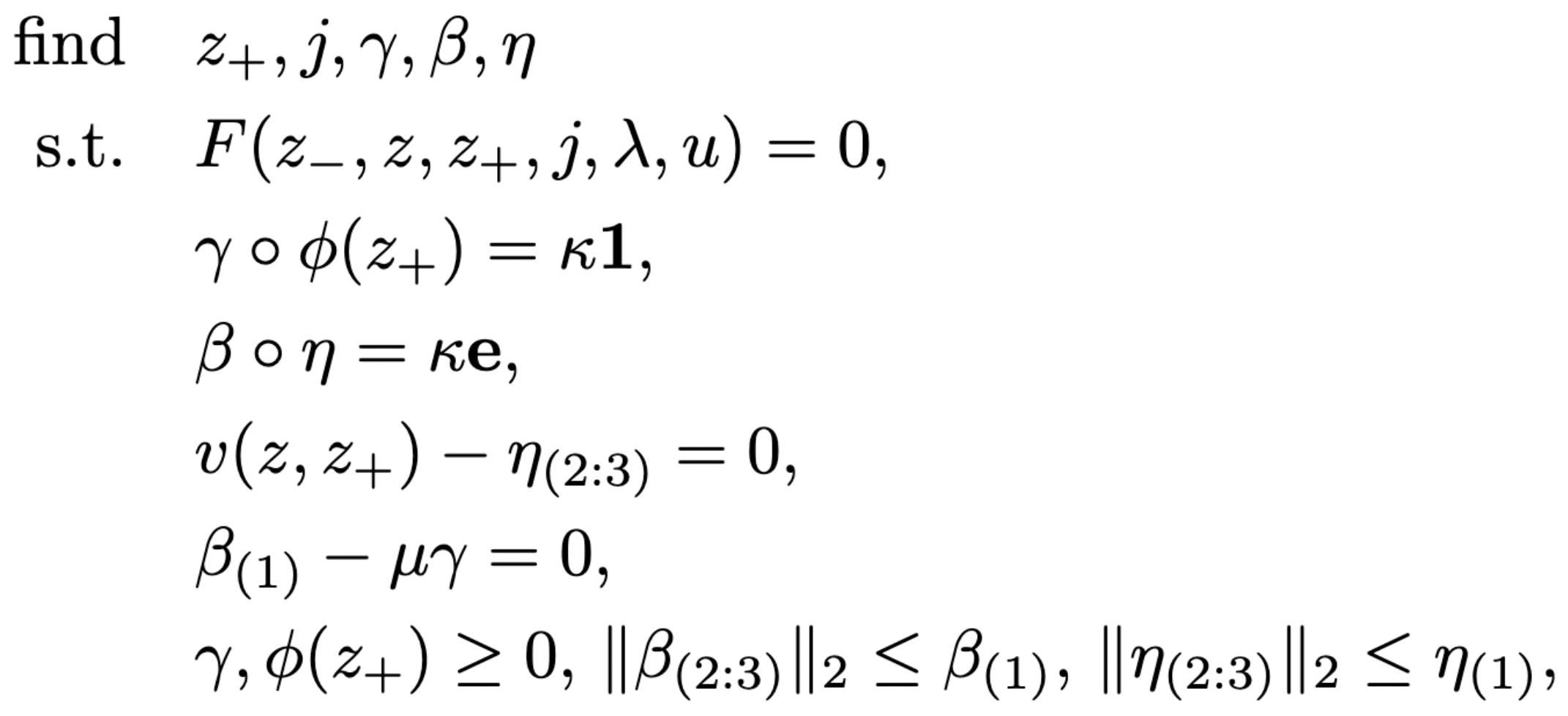
accurate contact dynamics

custom interior-point solver
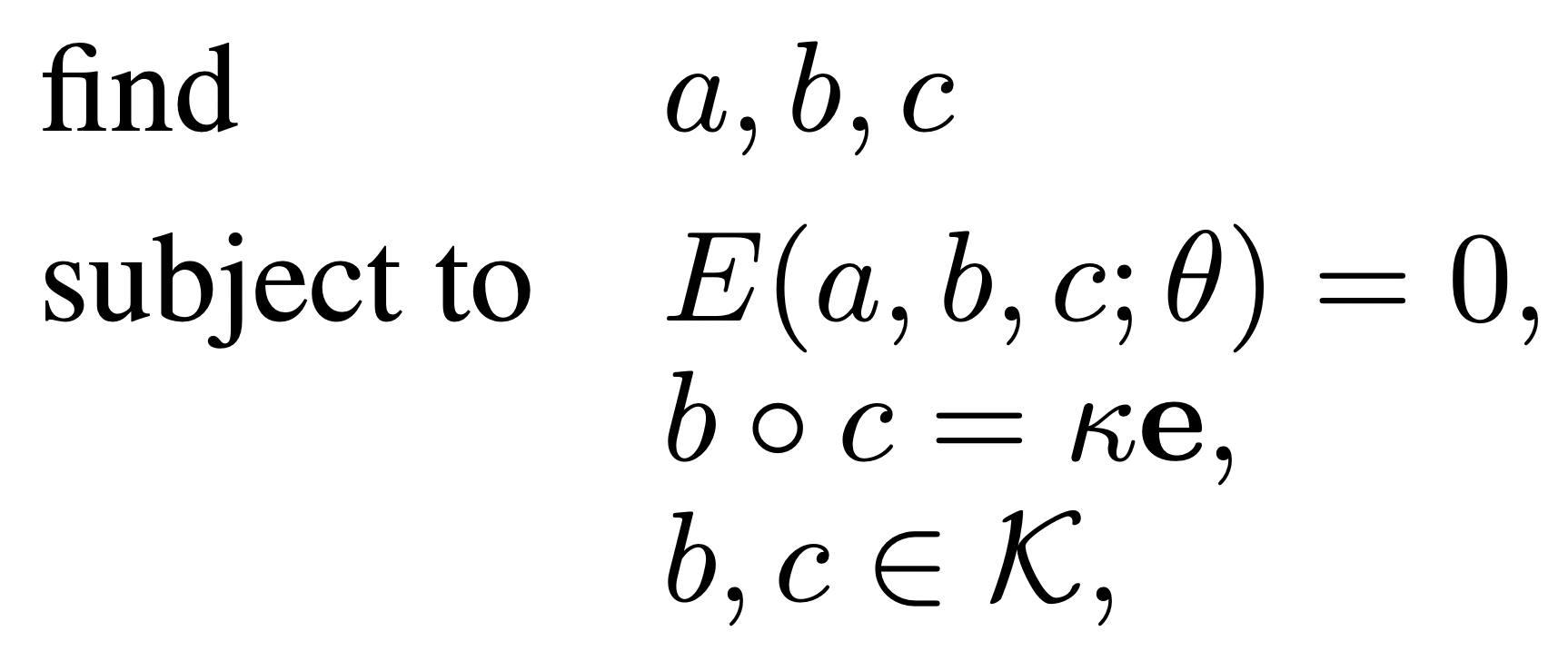
- Mehrotra predictor-corrector algorithm
- CVXOpt second-order cones
- non-Euclidean support for quaternions
accurate contact dynamics

→
smooth gradients
residual
solution
parameters
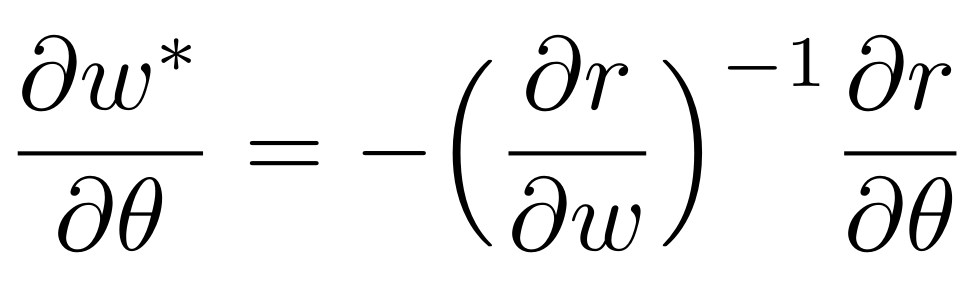
sensitivity of solution w.r.t problem data

computation cost of gradient is less than simulation step
differentiate intermediate barrier problems for smooth gradients
smooth gradients
Lezioni di analisi infinitesimale. U. Dini.
Dojo gradients vs sampling


box push
non-smooth dynamics
gradient comparison

Dojo
randomized smoothing
less expensive to compute compared to finite-difference or stochastic sampling
Dojo gradients vs sampling

less expensive to compute compared to finite-difference or stochastic sampling
randomized smoothing
finite difference
Dojo
matrix backward substitution
matrix factorization
matrix factorization
maximal-coordinates representation




minimal-coordinates
representation


maximal-coordinates
representation


maximal-coordinates representation
Linear-Time Variational Integrators in Maximal Coordinates. J. Brudigam and Z. Manchester.
Linear-Time Contact and Friction Dynamics in Maximal Coordinates using Variational Integrators.
J. Brudigam and Z. Manchester.


github.com/dojo-sim
- Julia package: Dojo.jl
- gym-like environments
- Python wrapper: dojopy
- interface w/ PyTorch & JAX


open-source implementation
examples

trajectory optimization


smooth-gradient-based optimization with iterative LQR



stability at low rates enables 2-5x sample-complexity improvement over MuJoCo
reinforcement learning


train static linear policies for locomotion

gradients enable 5-10x sample-complexity improvement over derivative-free method
stability at low rates enables 2-5x sample-complexity improvement over MuJoCo
system identification
ContactNets: Learning Discontinuous Contact Dynamics with Smooth, Implicit Representations. S. Pfrommer, M. Halm, and M. Posa.
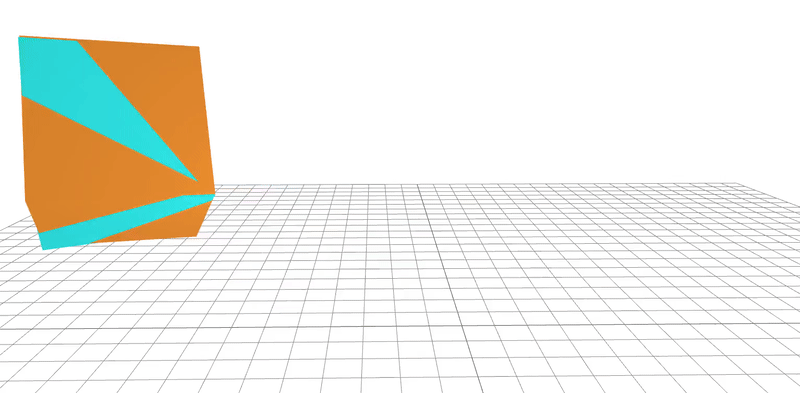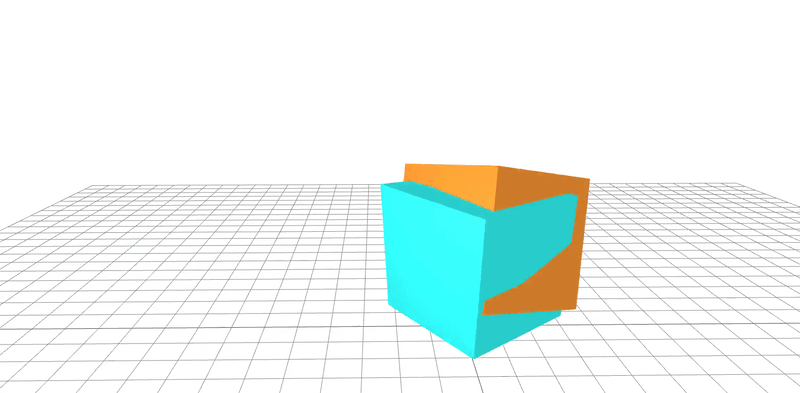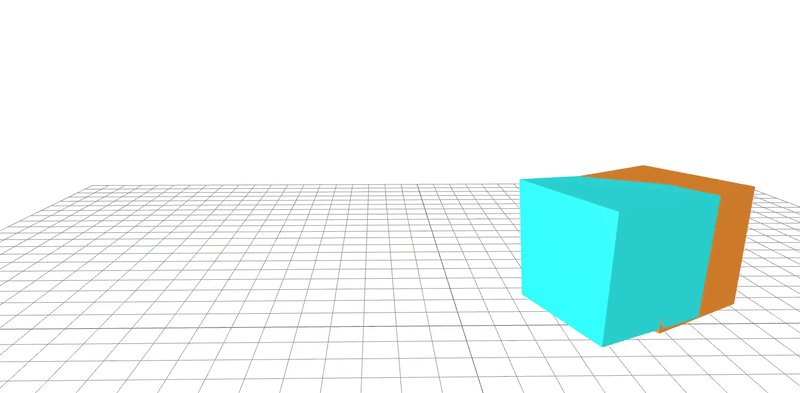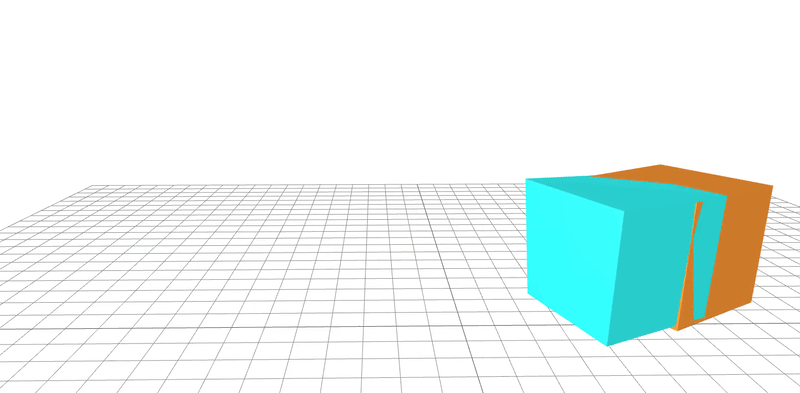
learned
ground-truth


real-word dataset
Dojo environment
system identification

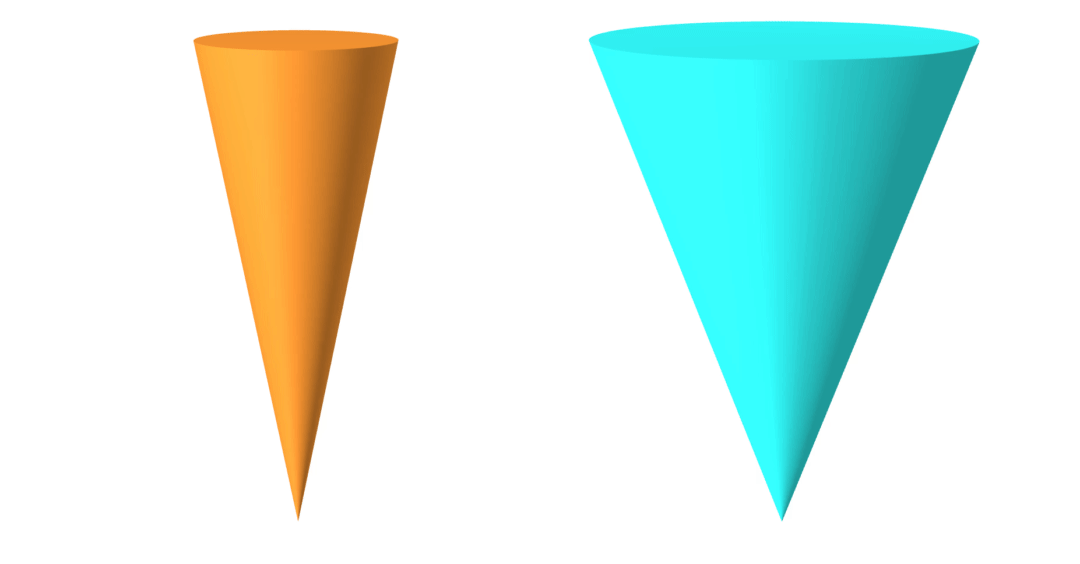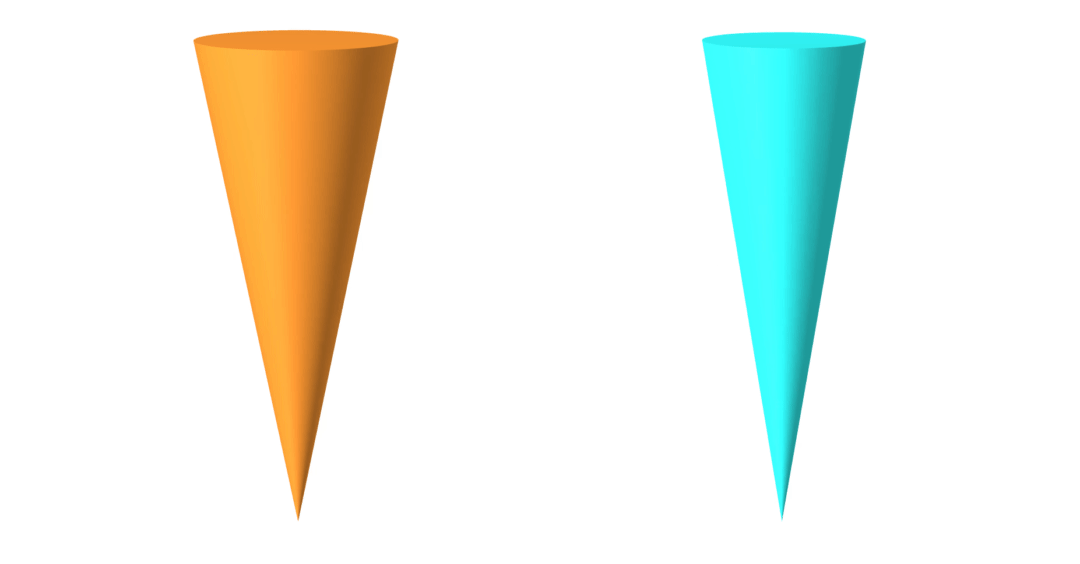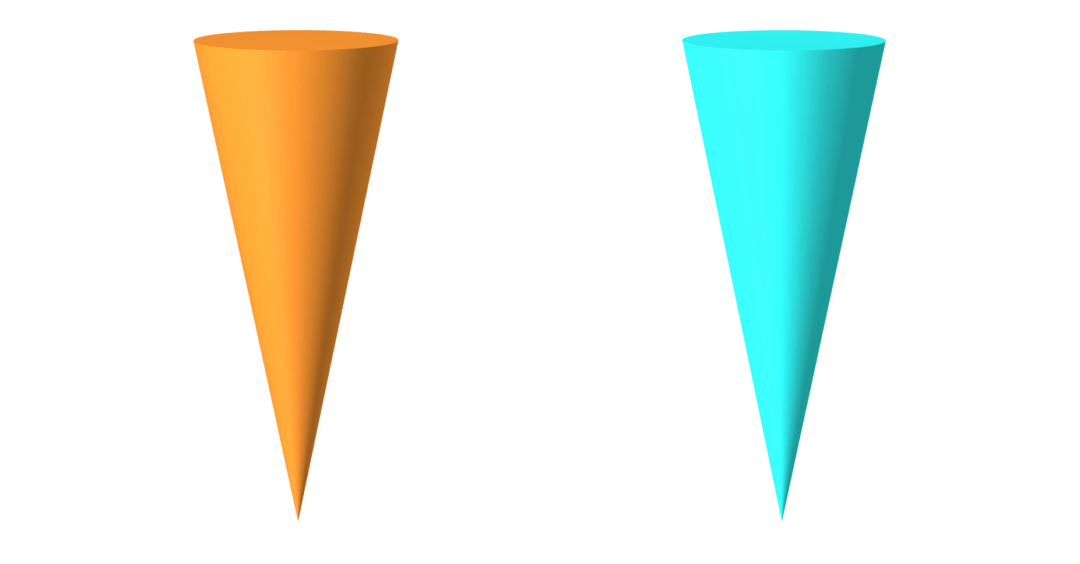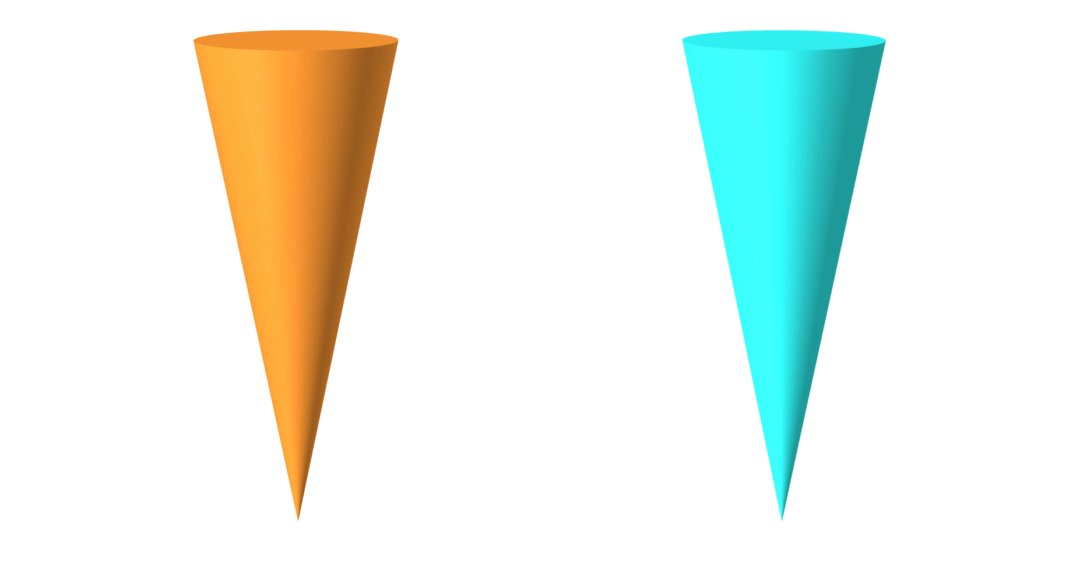
geometry
friction coefficient
ground-truth
learned

Quasi-Newton method utilizes gradients to
learn parameters to 95% accuracy in 20 steps
related work

Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasi-dynamic Contact Models, Tao Pang∗, H.J. Terry Suh∗, Lujie Yang and Russ Tedrake,
RRT using the same smoothed derivatives as Dojo

NeRF

Differentiable Physics Simulation of Dynamics-Augmented Neural Objects. S. Le Cleac'h, HX. Yu, M. Guo, T. Howell, R. Gao, J. Wu, Z. Manchester, M. Schwager
dynamics-augmented NeRF → complex collision geometries

model-predictive control


Fast Contact-Implicit Model-Predictive Control.
S. Le Cleac'h & T. Howell, C. Lee, S. Yang, M. Schwager, Z. Manchester


simulation
push recovery
behavior generation
running policy at 200-500Hz
strategic linearization
nonlinear complementarity problem (NCP)
impact force
strategic linearization
nonlinear complementarity problem (NCP)
impact force
slack variable
strategic linearization
nonlinear complementarity problem (NCP)
impact force
slack variable
strategic linearization
impact force
slack variable
nonlinear complementarity problem (NCP)
strategic linearization
strategic linearization
linear complementarity problem (LCP)
benefits of LCP formulation
preserve contact reasoning
→ adapt contact sequence online

benefits of LCP formulation
preserve contact reasoning
→ adapt contact sequence online
computational gains
→ real-time performance


contact-implicit MPC
contact-implicit MPC
contact-implicit MPC
contact-implicit MPC
dynamics evaluation
dynamics gradient
solve LCP problem
differentiate LCP problem
model-predictive control

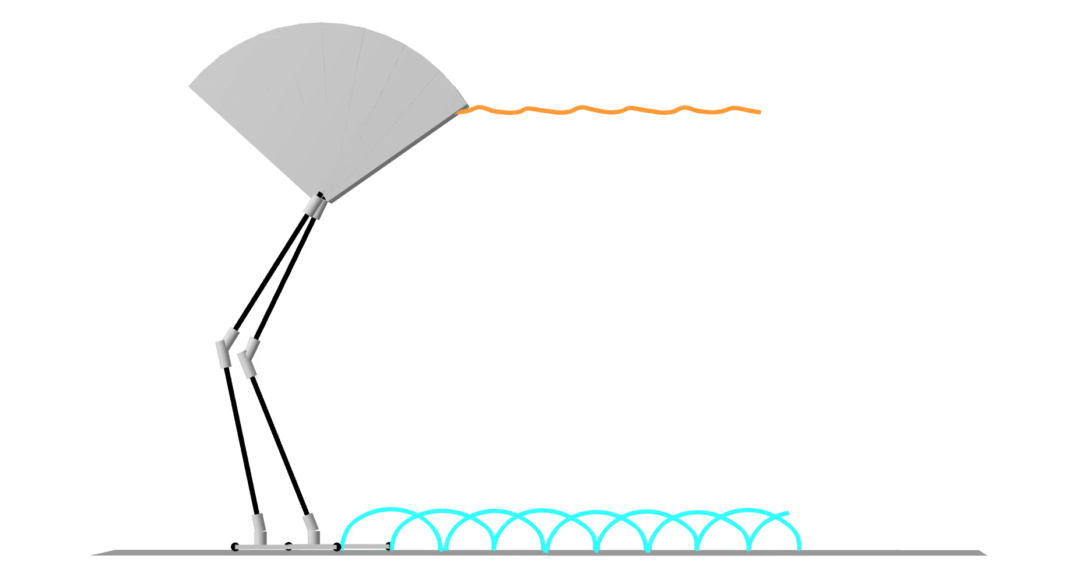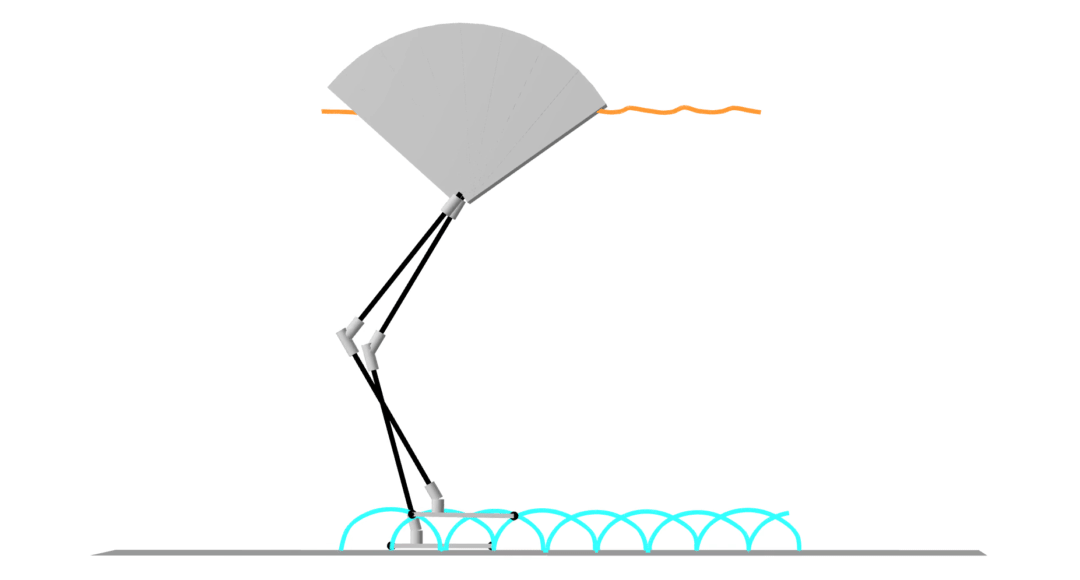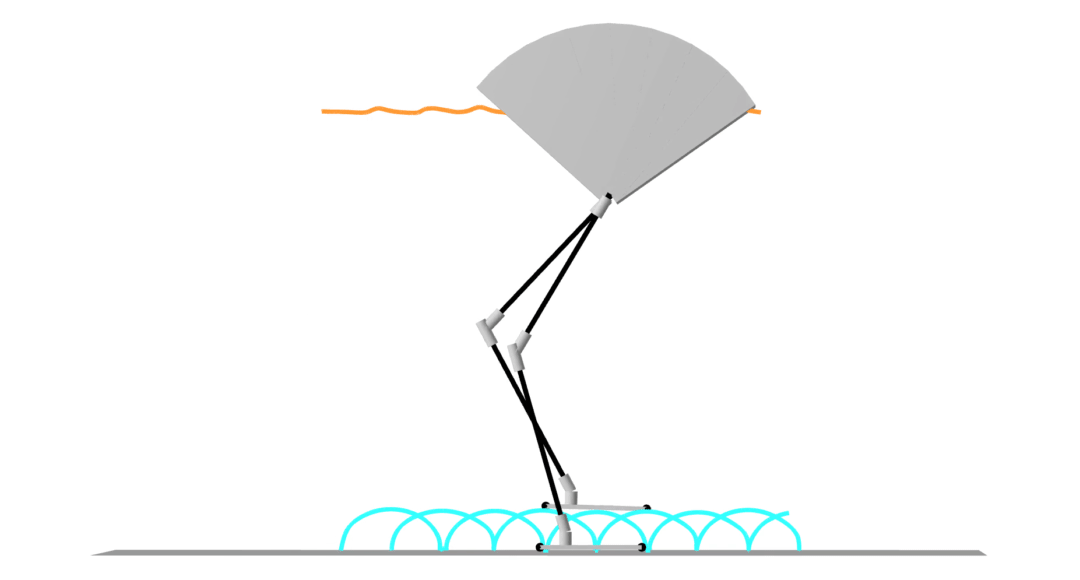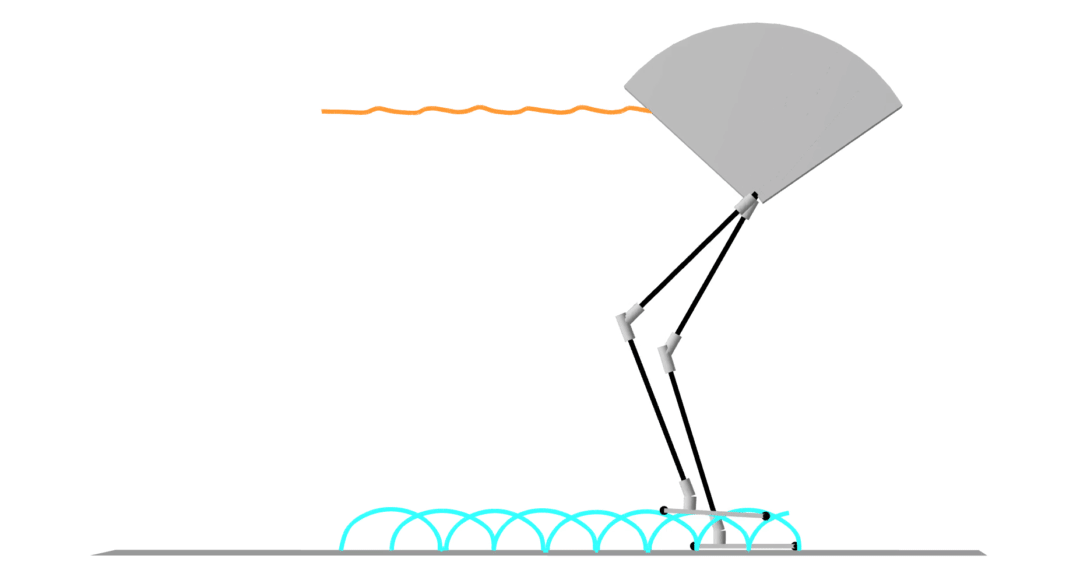
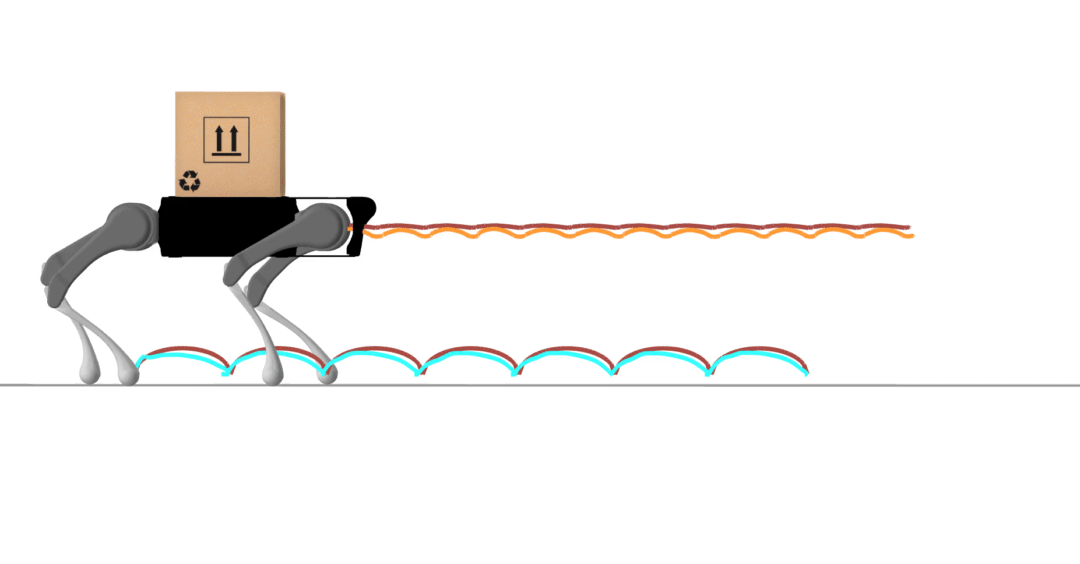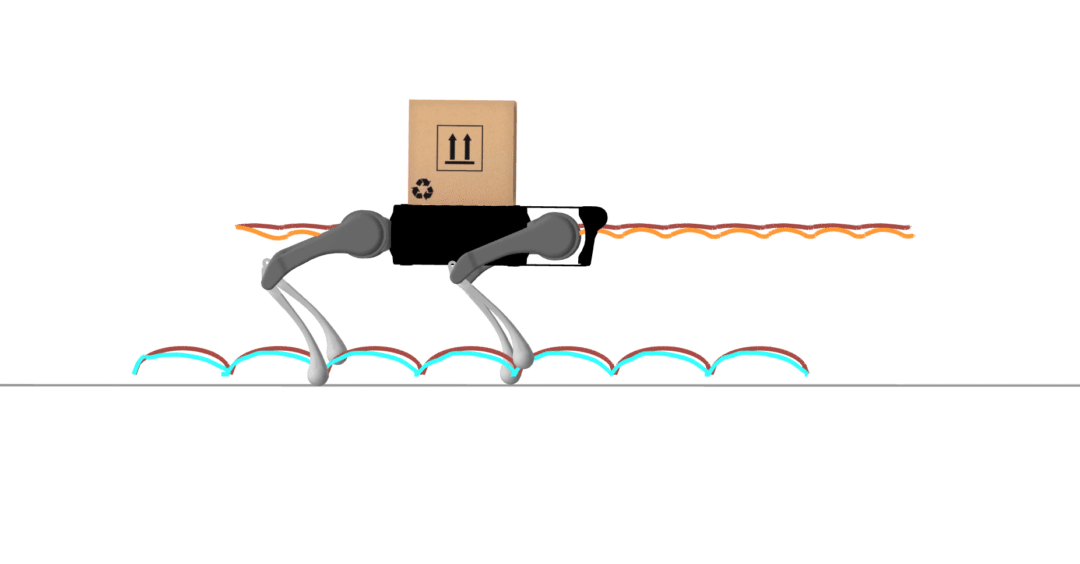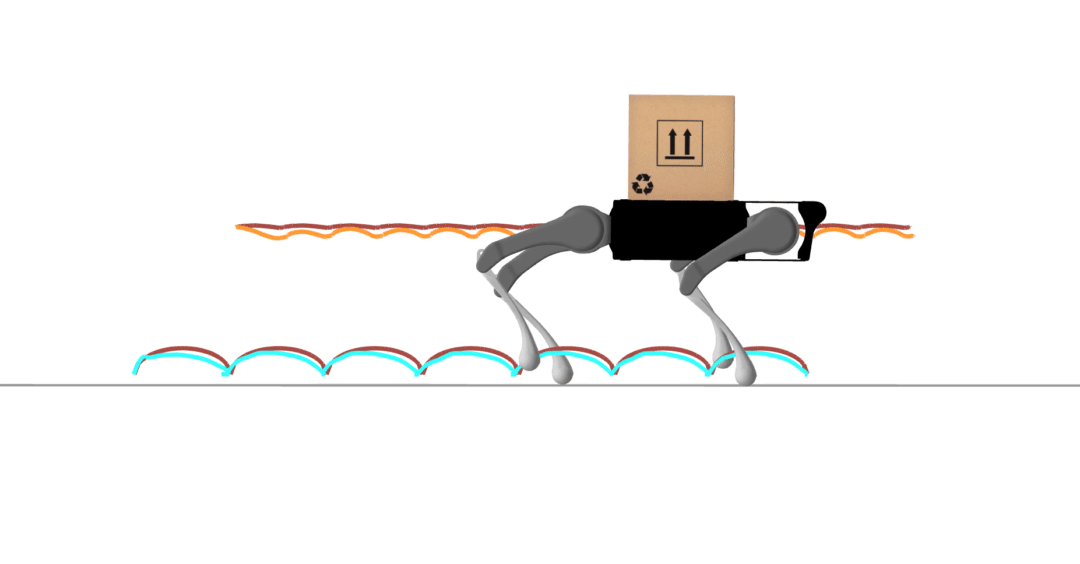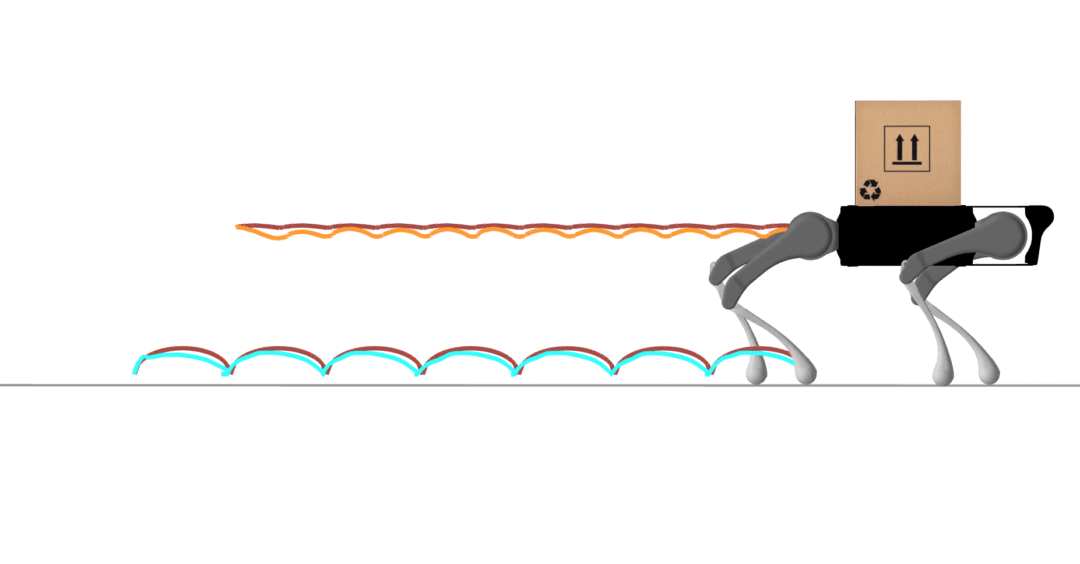




contact-implicit trajectory optimization
contact-implicit MPC
hardware transfer
model-predictive control

contact-implicit trajectory optimization
contact-implicit MPC
hardware transfer



model-predictive control

contact-implicit trajectory optimization
contact-implicit MPC
hardware transfer



model-predictive control







Taylor Howell
Simon Le Cleac'h
Jan Brüdigam
Zico Kolter
Mac Schwager
Zachary Manchester
team



Shuo Yang
Chi Yen Lee









github.com/dojo-sim
Apple
august 9, 2022
Simon Le Cleac'h
a differentiable physics engine for robotics
Simon Le Cleac'h and Taylor Howell




Taylor Howell
Simon Le Cleac'h
team

thowell@stanford.edu
simonlc@stanford.edu

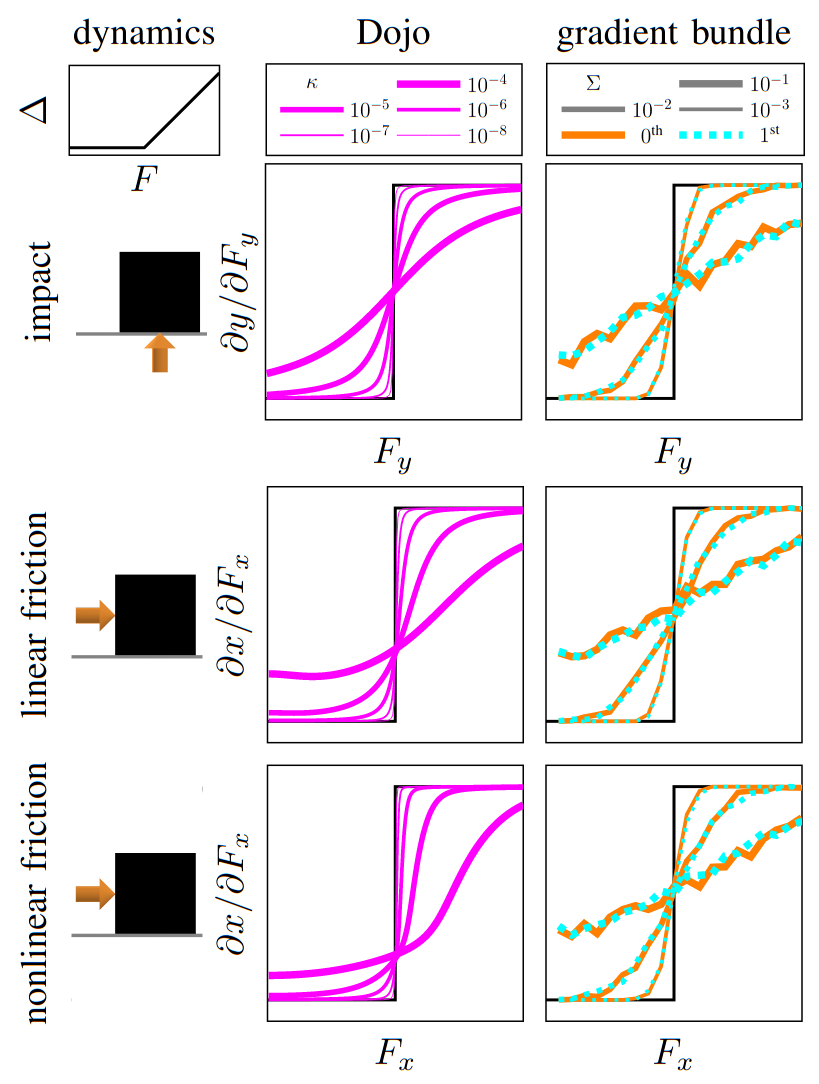
Dojo key ideas
minimal vs. maximal coordinates
benefits of differentiability
applications of Dojo
overview
contact physics

LCP
implicit complementarity
gradients
samples
subgradient
existing physics engines




Dojo key ideas
stability at low rates
variational integrator
interior-point methods
accurate contact dynamics
implicit differentiation
smooth gradients




Discrete mechanics and variational integrators. J. E. Marsden and M. West.
discretize
discretize
Euler-Lagrange
Euler-Lagrange


variational integrator
variational integrator
-
compare astronaut energy and momentum conservation to MuJoCo

- Dojo performs orders of magnitude better
- stability at low rates
accurate contact dynamics


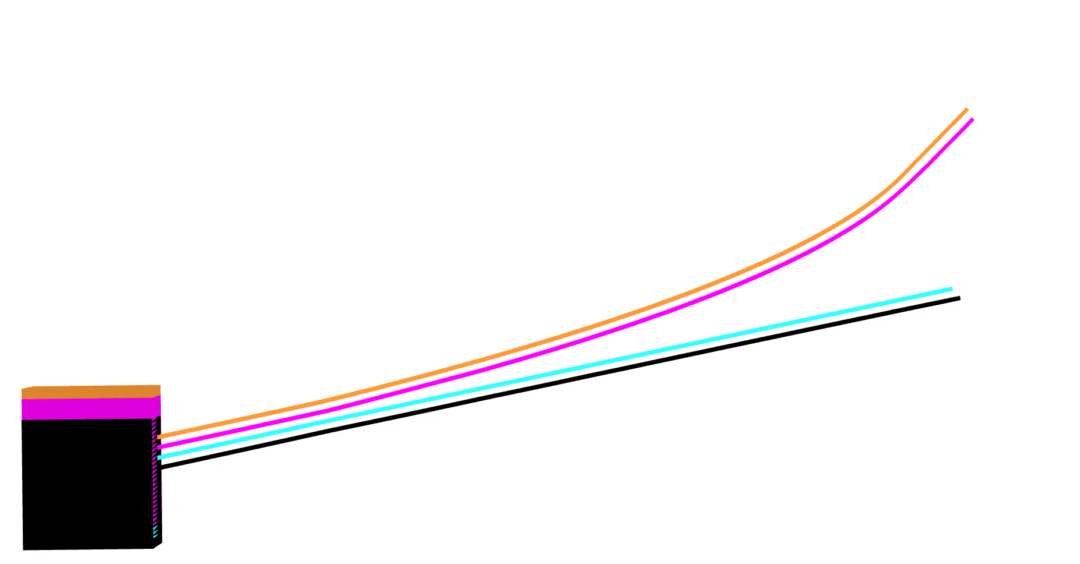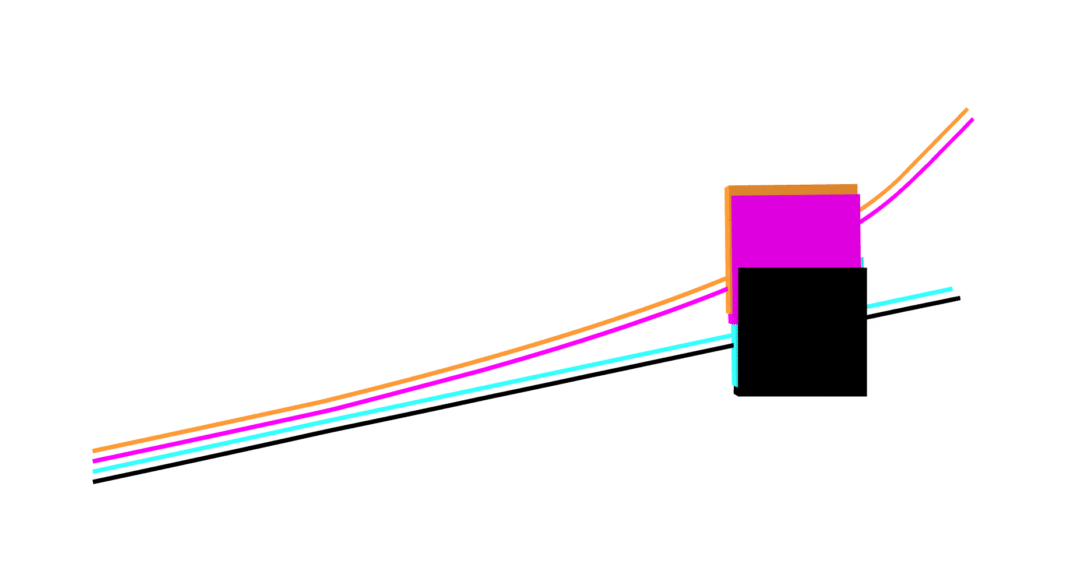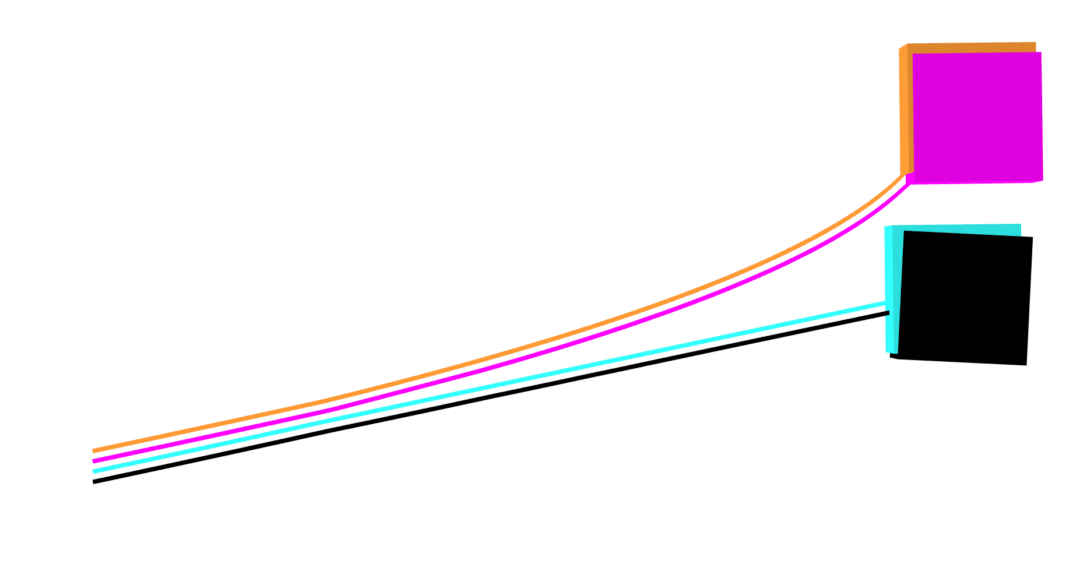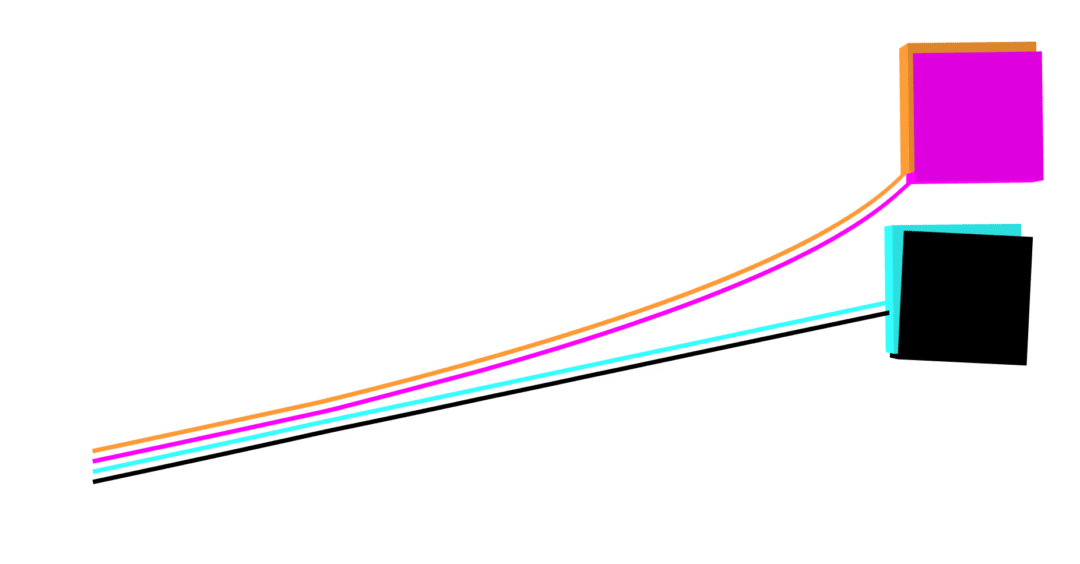
MuJoCo linear
Dojo linear
MuJoCo nonlinear
Dojo nonlinear
no collision violations
correct Coulomb friction
interior-point method
impact → inequalities
friction → second-order cone
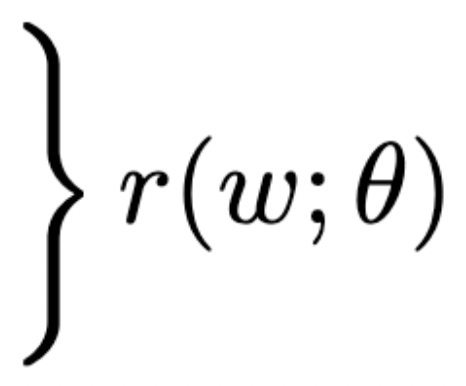
non linear complementarity problem

nonlinear complementarity problem
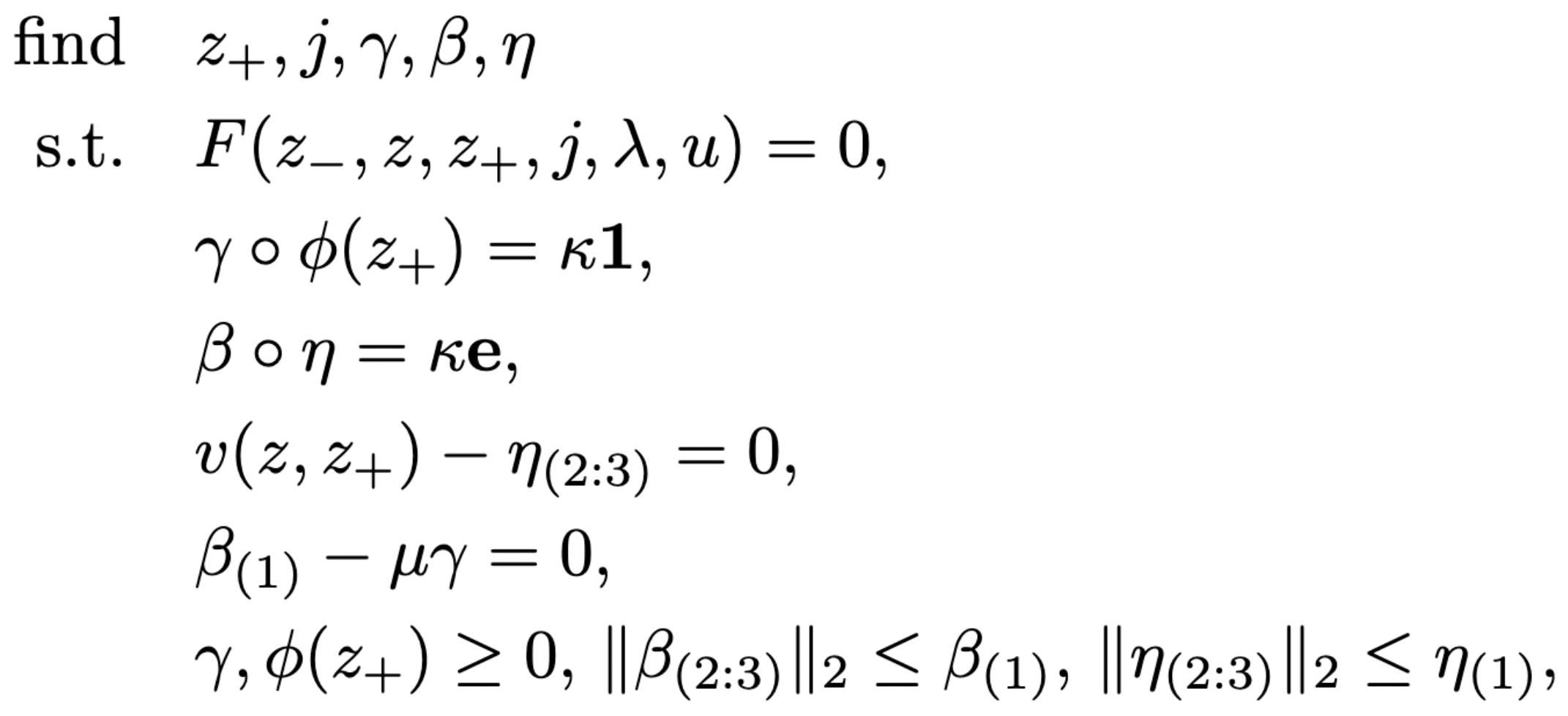
accurate contact dynamics

custom interior-point solver
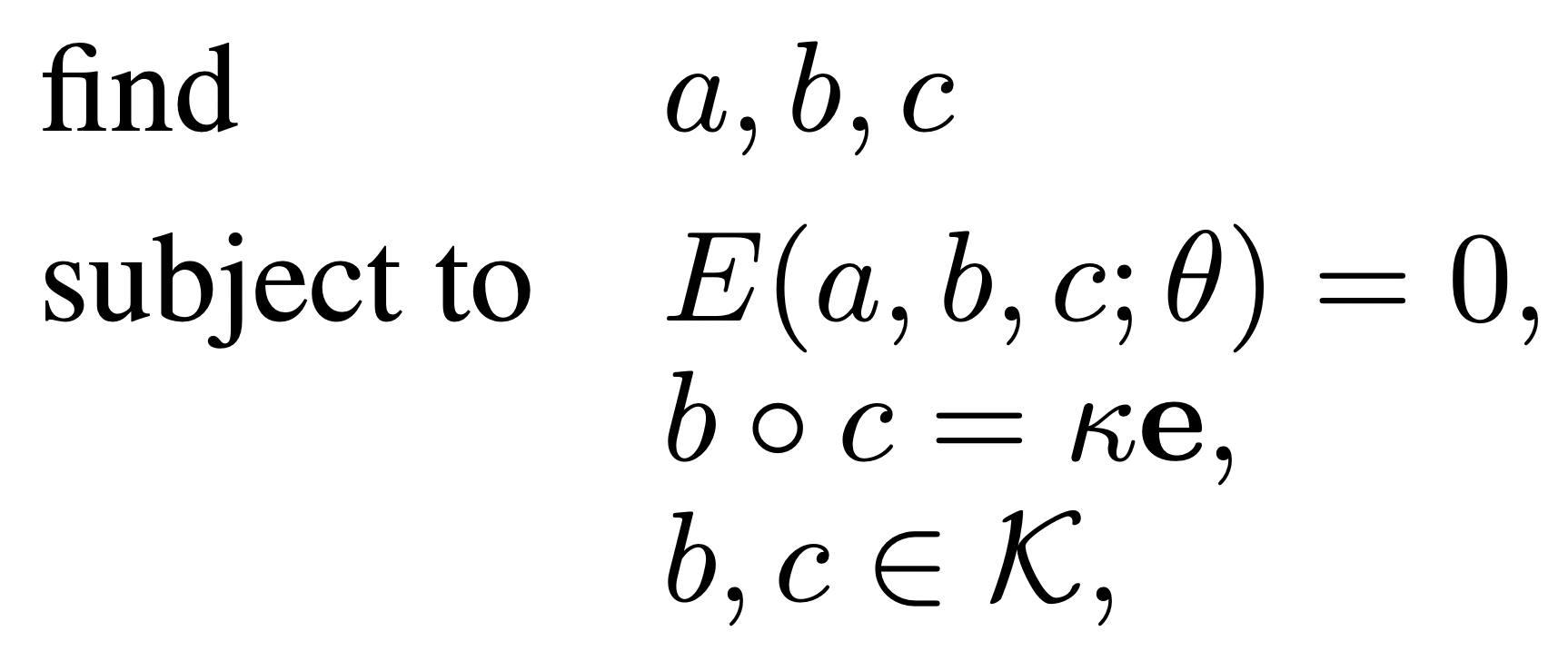
- Mehrotra predictor-corrector algorithm
- CVXOpt second-order cones
- non-Euclidean support for quaternions
accurate contact dynamics

→
smooth gradients
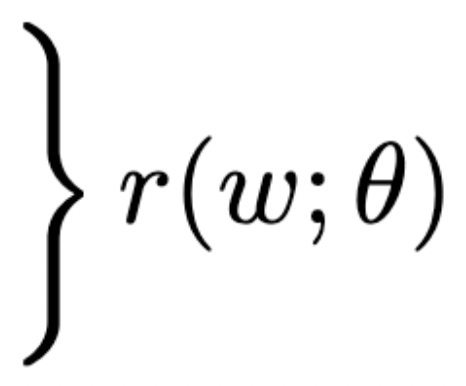
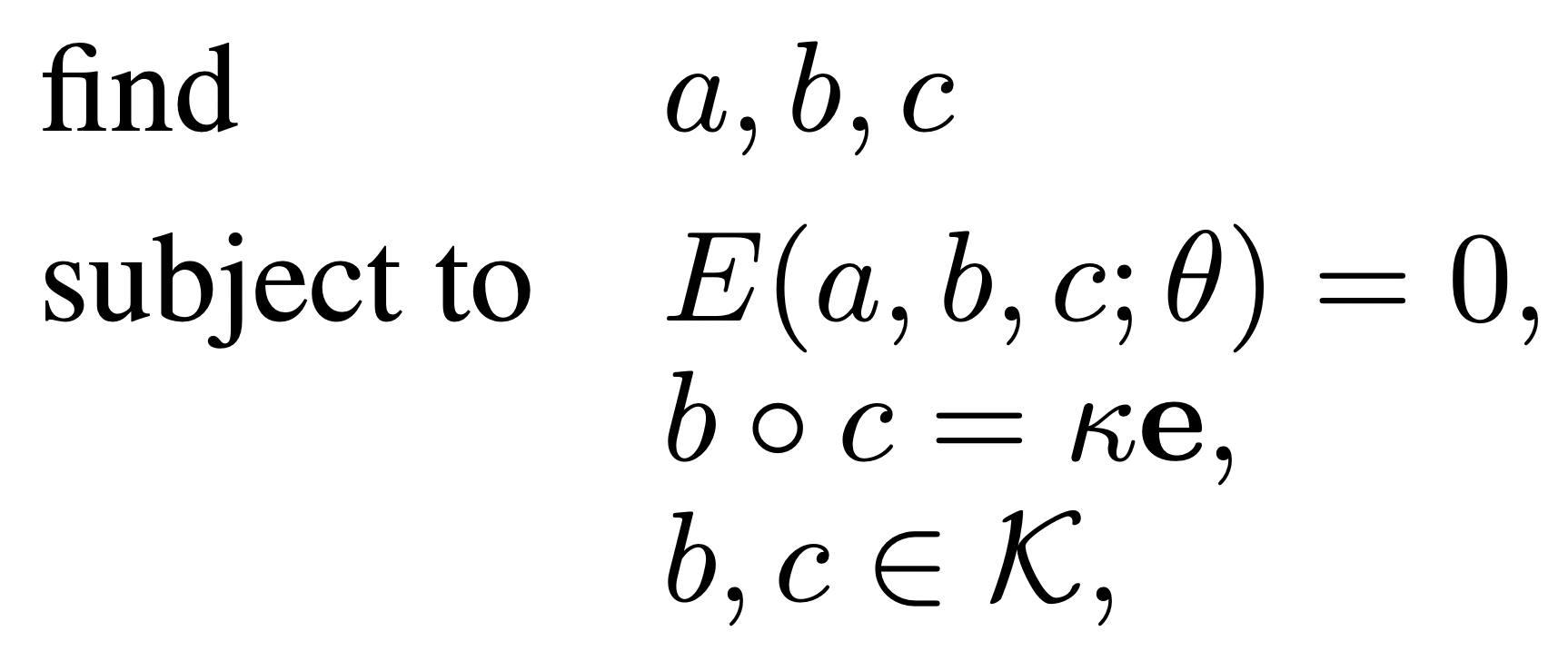
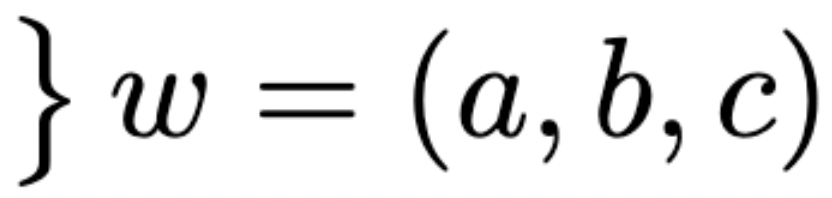
residual
solution
parameters
nonlinear complementarity problem
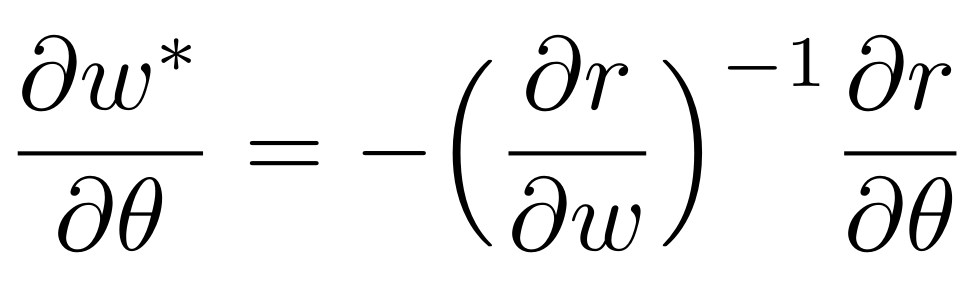
sensitivity of solution w.r.t problem data

computation cost of gradient is less than simulation step
differentiate intermediate barrier problems for smooth gradients
smooth gradients
Lezioni di analisi infinitesimale. U. Dini.

less expensive to compute compared to finite-difference or stochastic sampling
randomized smoothing
finite difference
Dojo
matrix backward substitution
matrix factorization
matrix factorization
smooth gradients


box push
non-smooth dynamics
gradient comparison

Dojo
randomized smoothing
less expensive to compute compared to finite-difference or stochastic sampling
smooth gradients
maximal-coordinates representation




minimal-coordinates
representation


maximal-coordinates
representation


maximal-coordinates representation
Linear-Time Variational Integrators in Maximal Coordinates. J. Brudigam and Z. Manchester.
Linear-Time Contact and Friction Dynamics in Maximal Coordinates using Variational Integrators.
J. Brudigam and Z. Manchester.


maximal-coordinates representation




github.com/dojo-sim
- Julia package: Dojo.jl
- gym-like environments
- Python wrapper: dojopy
- interface w/ PyTorch & JAX


open-source implementation
examples

trajectory optimization


smooth-gradient-based optimization with iterative LQR



stability at low rates enables 2-5x sample-complexity improvement over MuJoCo
reinforcement learning


train static linear policies for locomotion

gradients enable 5-10x sample-complexity improvement over derivative-free method
stability at low rates enables 2-5x sample-complexity improvement over MuJoCo
system identification
ContactNets: Learning Discontinuous Contact Dynamics with Smooth, Implicit Representations. S. Pfrommer, M. Halm, and M. Posa.
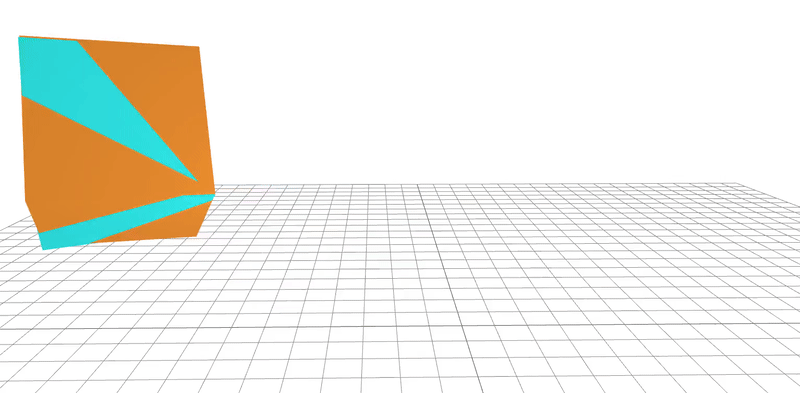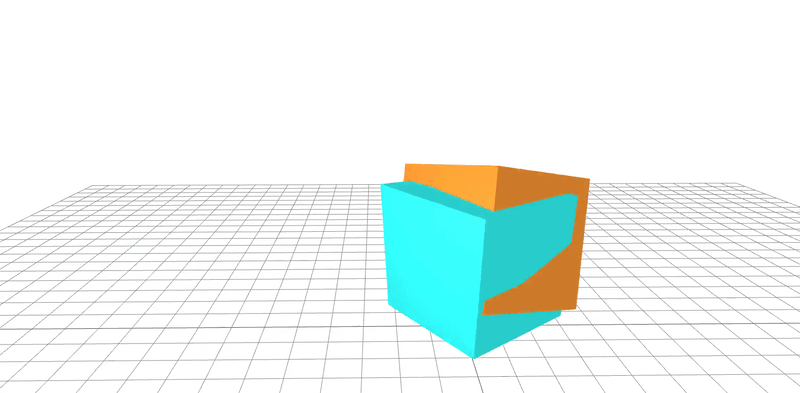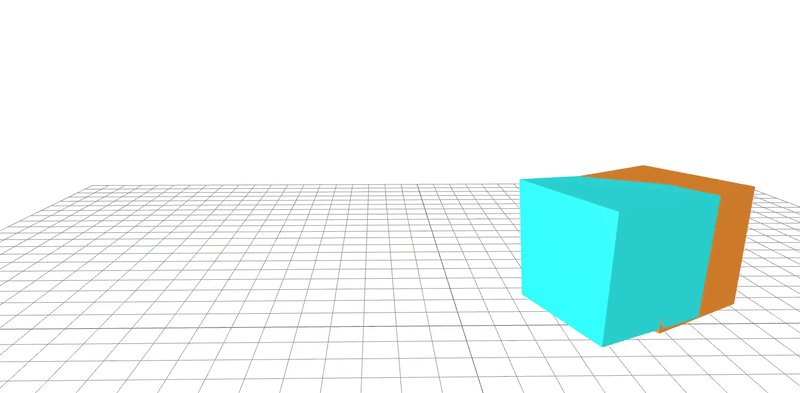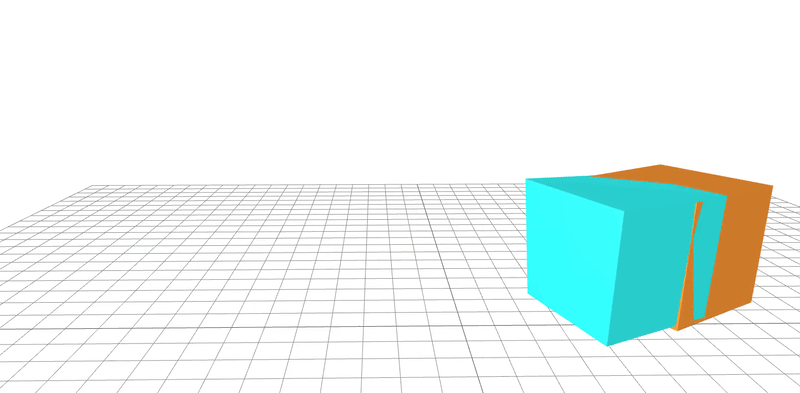
learned
ground-truth


real-word dataset
Dojo environment
system identification

geometry
friction coefficient
ground-truth
learned

Quasi-Newton method utilizes gradients to
learn parameters to 95% accuracy in 20 steps



contact-implicit trajectory optimization
contact-implicit MPC
hardware transfer
model-predictive control

contact-implicit trajectory optimization
contact-implicit MPC
hardware transfer



model-predictive control

contact-implicit trajectory optimization
contact-implicit MPC
hardware transfer



model-predictive control

model-predictive control


Fast Contact-Implicit Model-Predictive Control.
S. Le Cleac'h & T. Howell, C. Lee, S. Yang, M. Schwager, Z. Manchester


simulation
push recovery
behavior generation
running policy at 200-500Hz
NeRF

Differentiable Physics Simulation of Dynamics-Augmented Neural Objects. S. Le Cleac'h, HX. Yu, M. Guo, T. Howell, R. Gao, J. Wu, Z. Manchester, M. Schwager
dynamics-augmented NeRF → complex collision geometries







Taylor Howell
Simon Le Cleac'h
Jan Brüdigam
Zico Kolter
Mac Schwager
Zachary Manchester
team



Shuo Yang
Chi Yen Lee









github.com/dojo-sim
systemX
march 4, 2022
Simon Le Cleac'h and Taylor Howell
Dojo:
A differentiable simulator for robotics
Simon Le Cleac'h and Taylor Howell

a simulator for robotics that prioritizes
physical accuracy
and
differentiability









isn't simulation a solved problem?

impact

Dojo
MuJoCo


friction
Dojo
- nonlinear (blue)
- linear (orange)
MuJoCo
- nonlinear (black)
- linear (magenta)
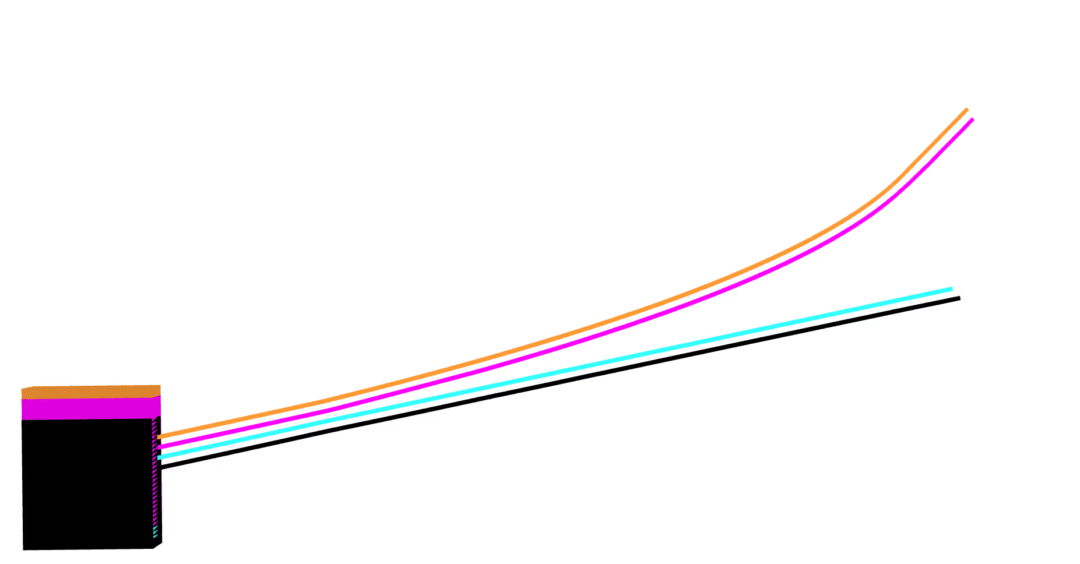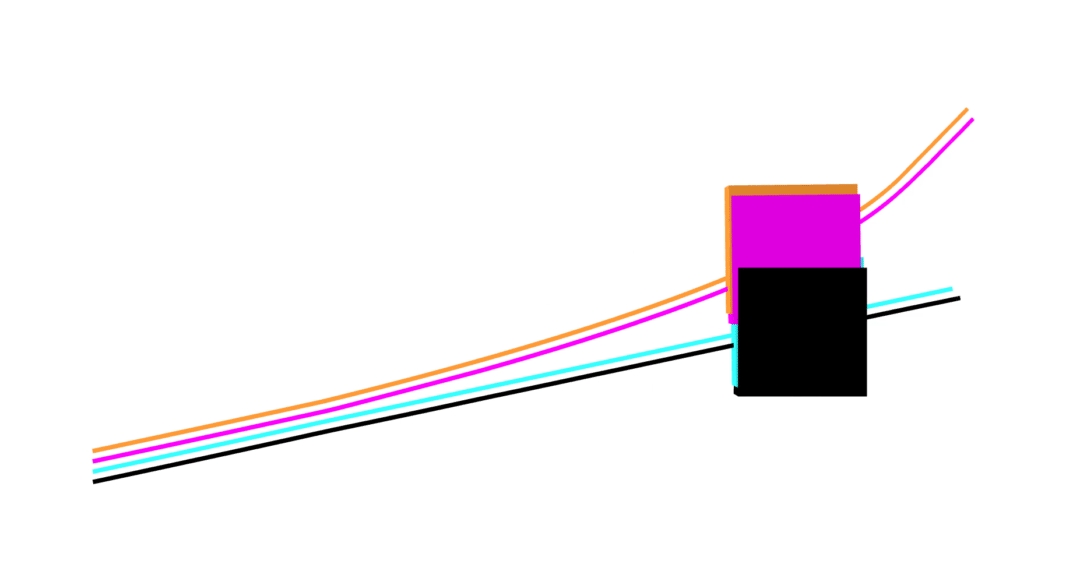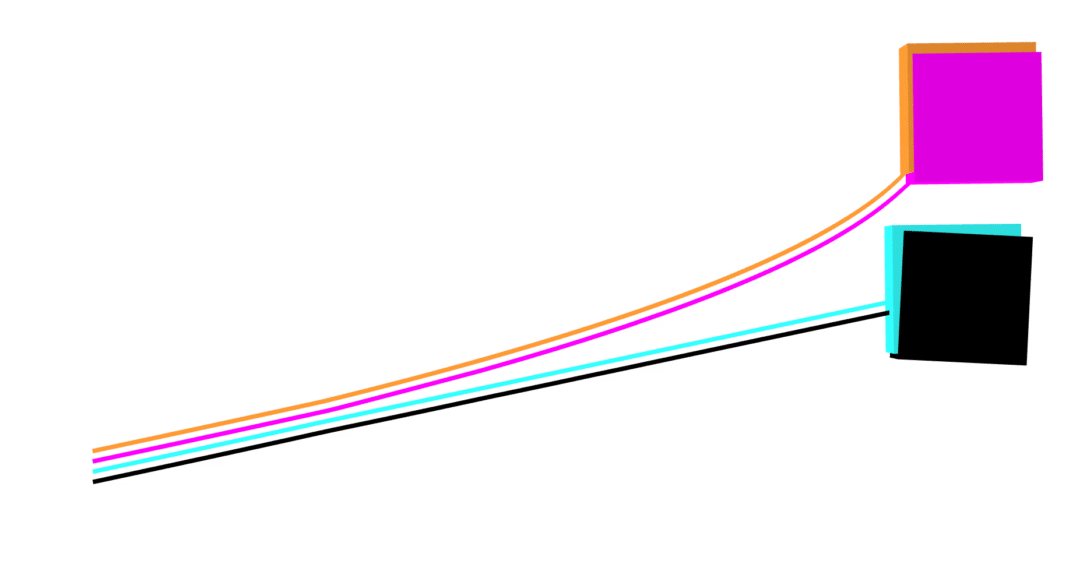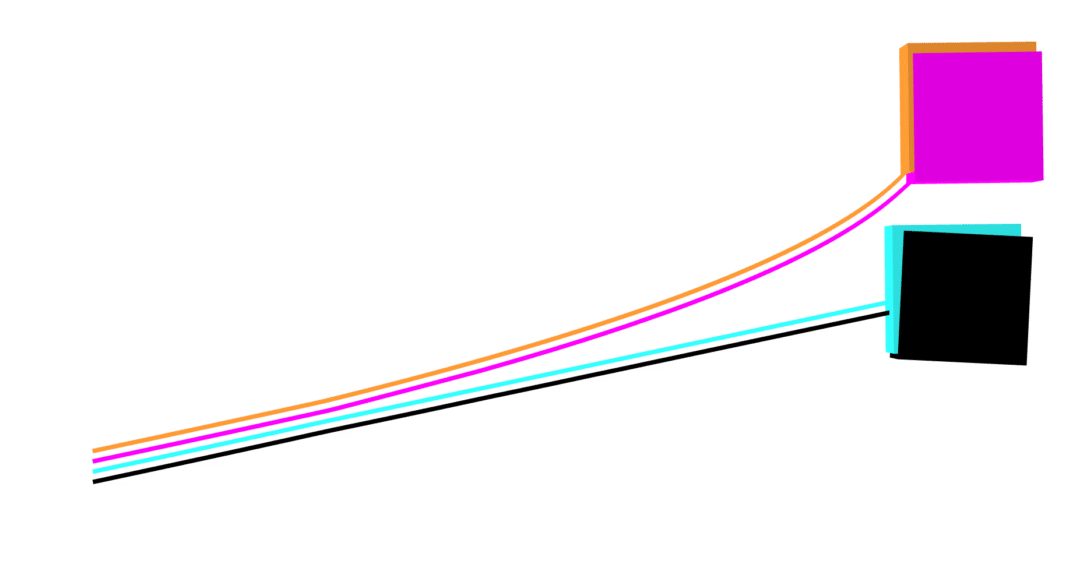


friction cones

approximation
exact

gradients

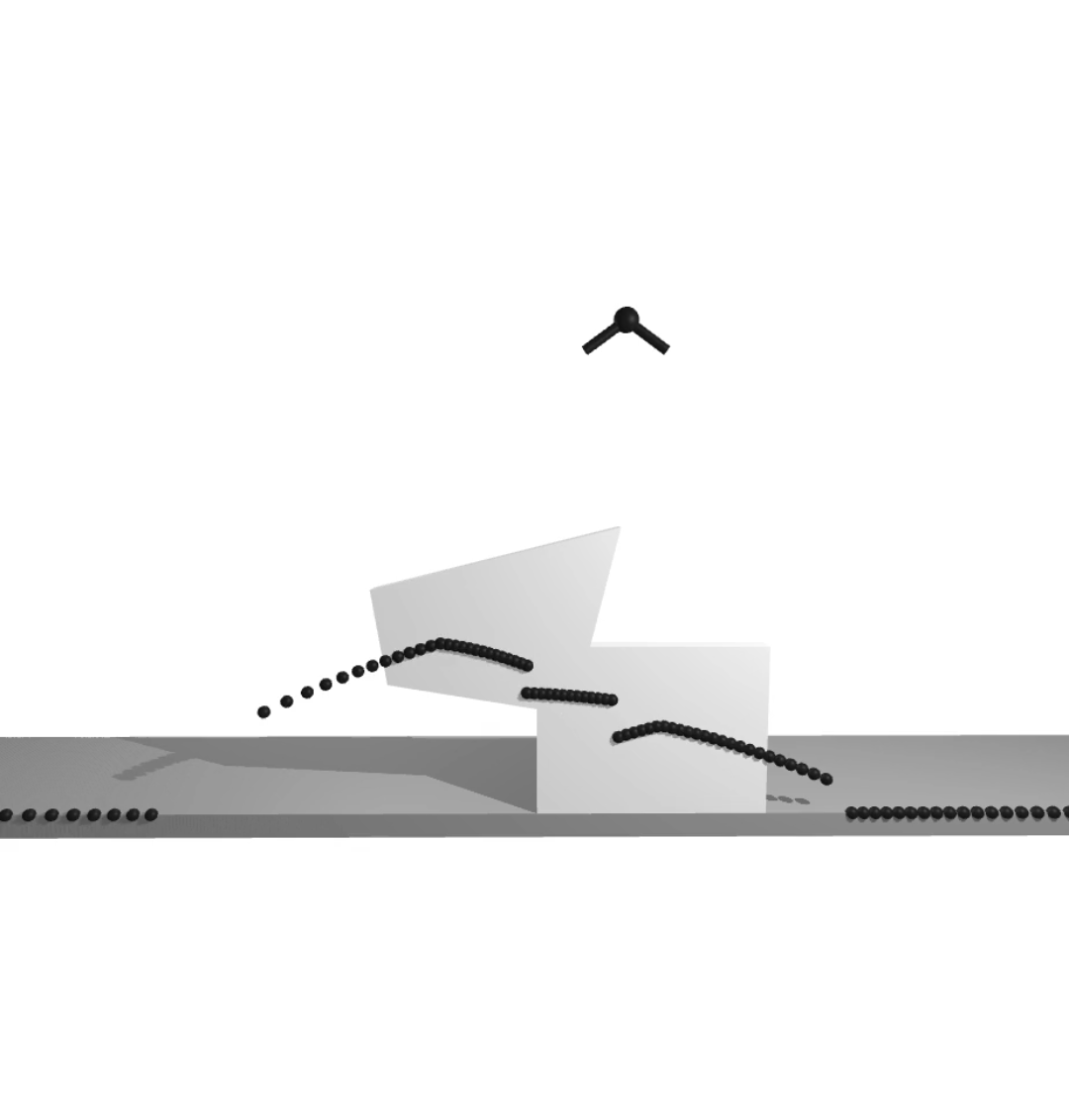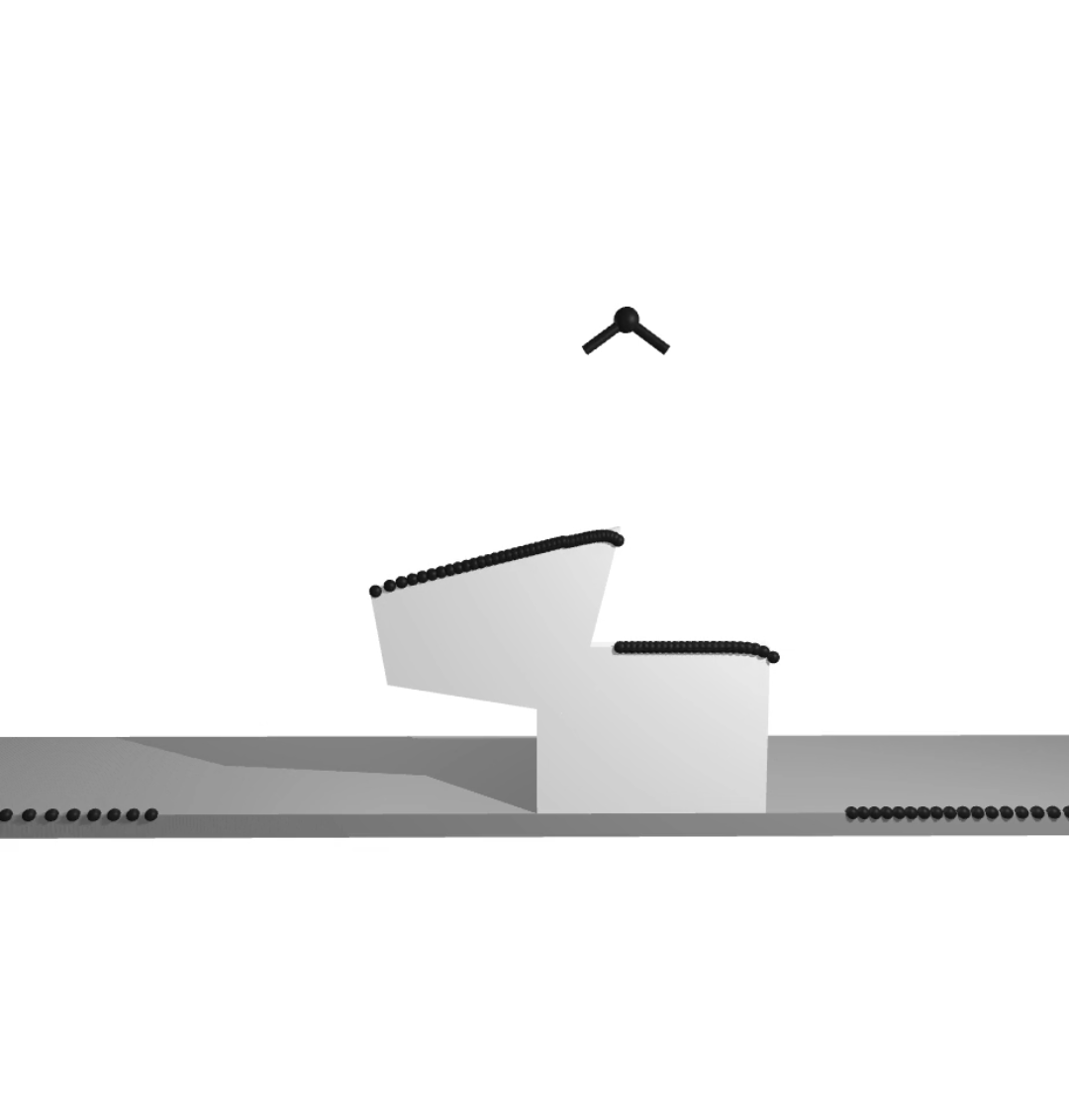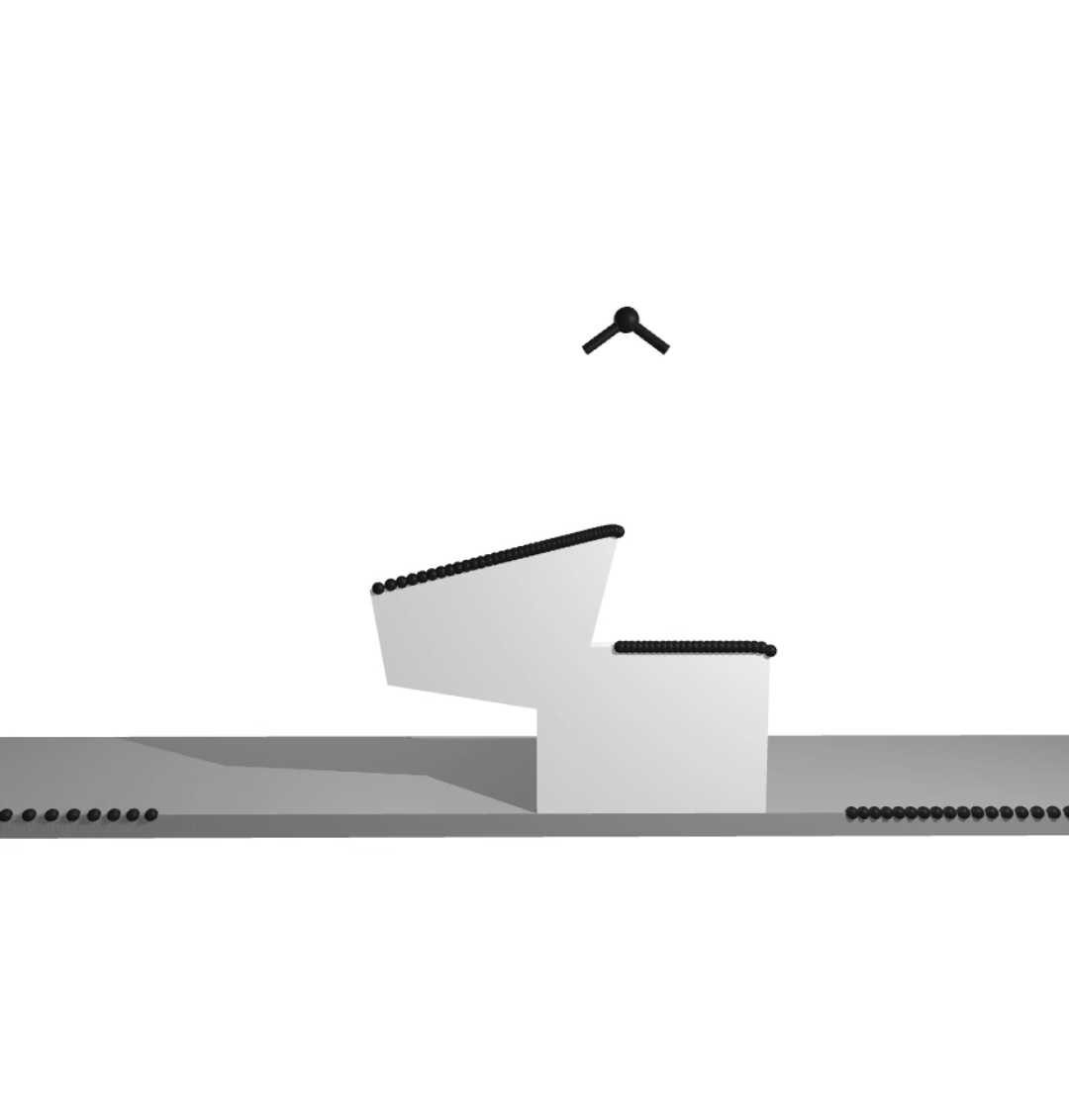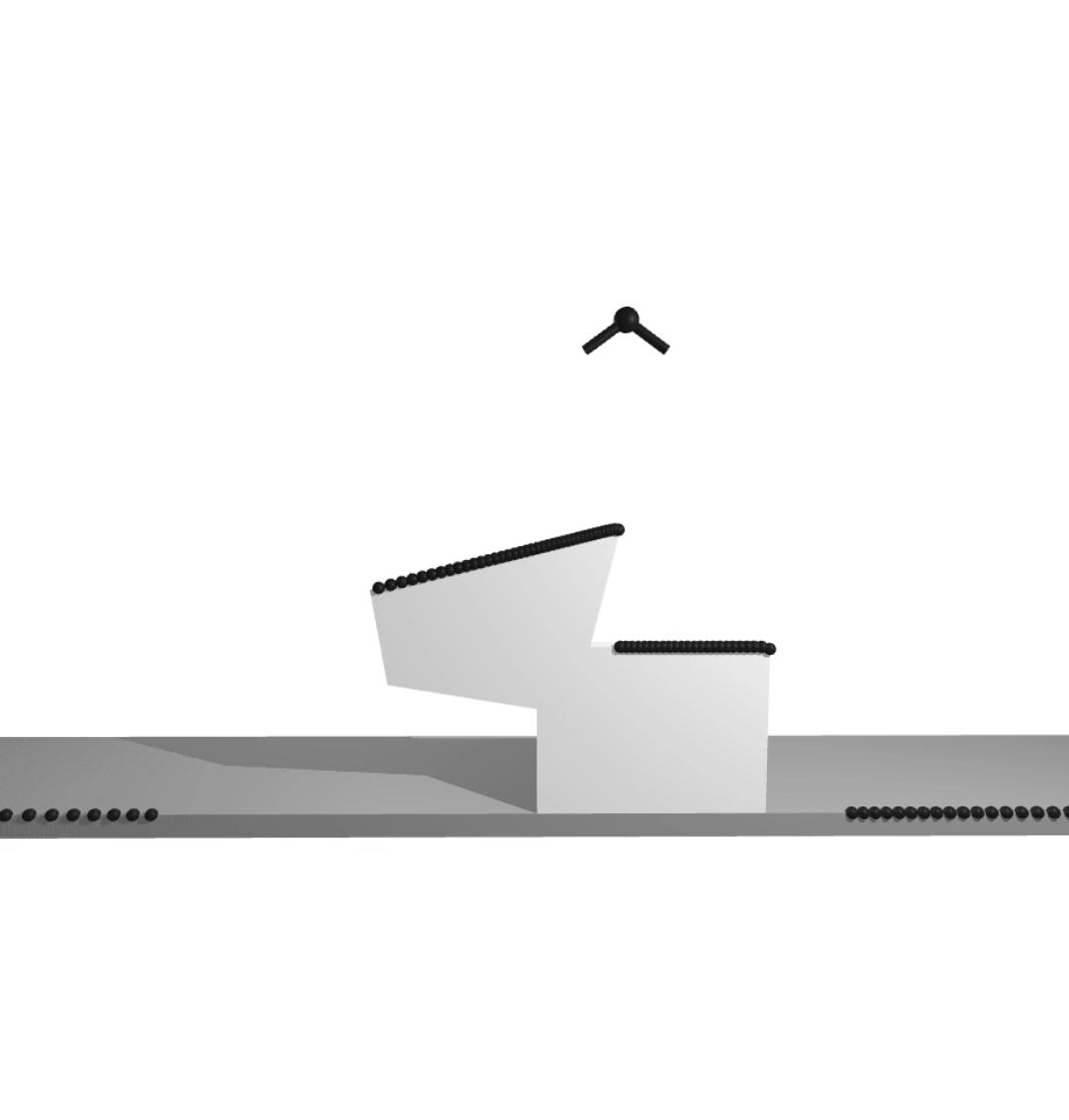
task: push object up to goal

gradients


code:
https://github.com/dojo-sim
paper:
https://arxiv.org/abs/2203.00806


collaborations
simonlc@stanford.edu (Simon)
thowell@stanford.edu (Taylor)

- manipulation
- reinforcement learning
-
open-source development
- GPU support
- advanced collision detection
