Neural Rendering
From Beginner
YiDar, Tang
2022 Feb
Replay
Content
- Introduction and Applications to Neural Rendering
- NeRF-Based Algorithms
- Text2Mesh
- Resources
- Introduction and Applications to Neural Rendering
- NeRF-Based Algorithms
- Text2Mesh
- Resources
Introduction and Applications to Neural Rendering

Neural Rendering, a definition:
Deep neural network for image or video generation that
enable explicit or implicit control of scene properties
Neural Rendering, a definition:
Deep neural network for image or video generation that
enable explicit or implicit control of scene properties
Generative networks that synthesize pixels
Neural Rendering, a definition:
Deep neural network for image or video generation that
enable explicit or implicit control of scene properties
Generative networks that synthesize pixels
Controllable by interpretable parameters or by conditioning input
Neural Rendering, a definition:
Deep neural network for image or video generation that
enable explicit or implicit control of scene properties
Generative networks that synthesize pixels
Controllable by interpretable parameters or by conditioning input
Illumination, camera, pose, geometry, appearance, semantic structure, animation, ...

Inference


Deferred Neural Rendering: Image Synthesis using Neural Textures

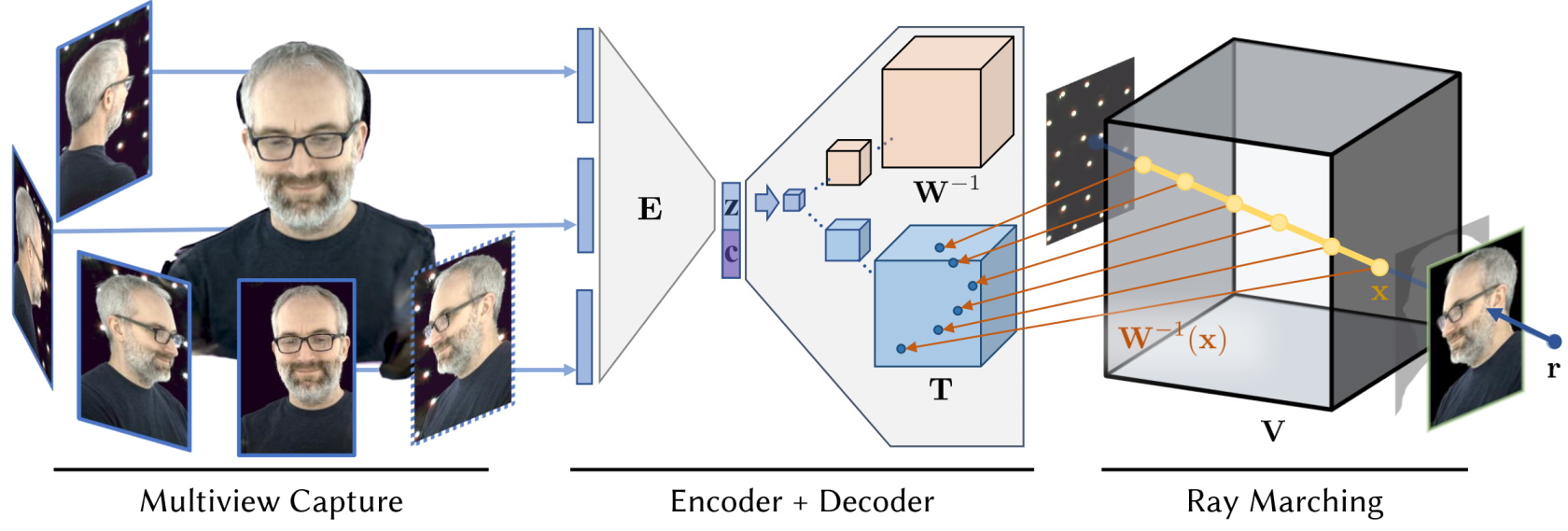
Nerual Volumes

Detail in the next section
Applications
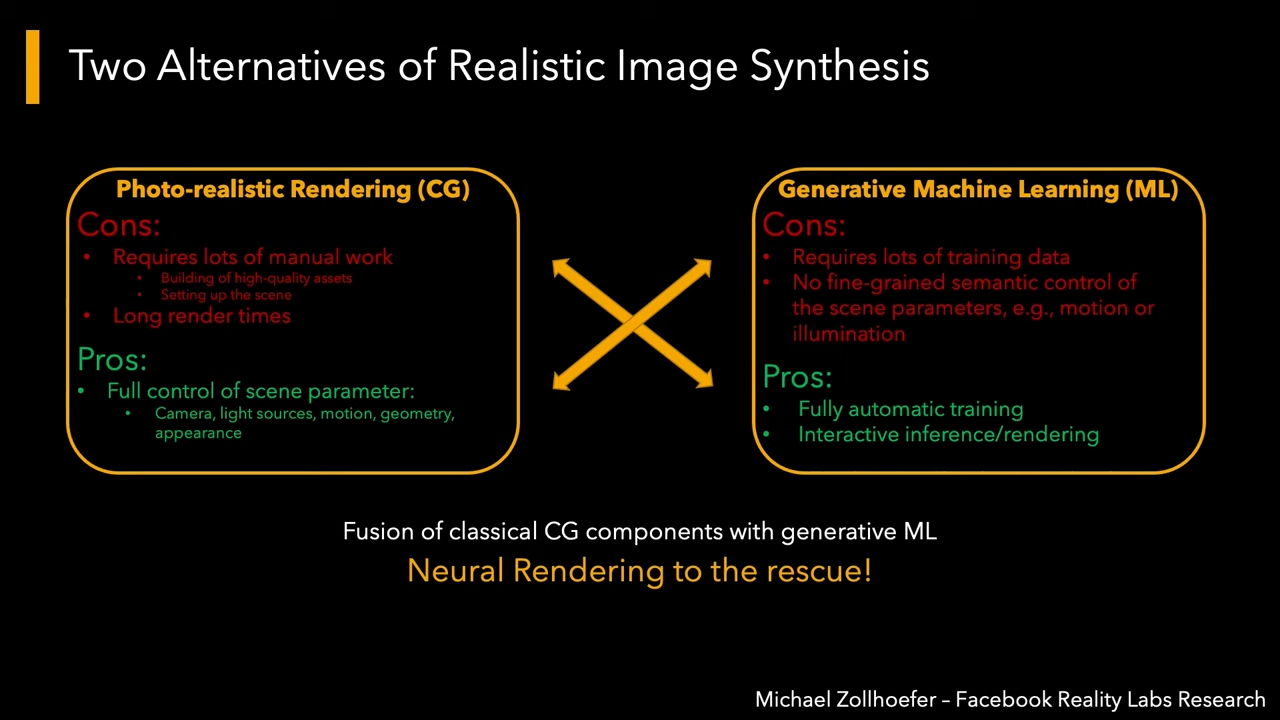
- Semantic Photo Synthesis (w/o CG tech)
- Novel View Synthesis of Static Content
- Generalization over Object and Scene Classes
- Learning to Represent and Render Non-static Content
- Compositionality and Editing
- Relighting and Material Editing
Notes:
"Semantic Photo Synthesis" is listed in the 2020 Apr paper "State of the Art on Neural Rendering"
2~6 are listed in the 2021 Nov Paper "Advances in Neural Rendering"
Semantic Photo Synthesis

(2018) GAN Dissection
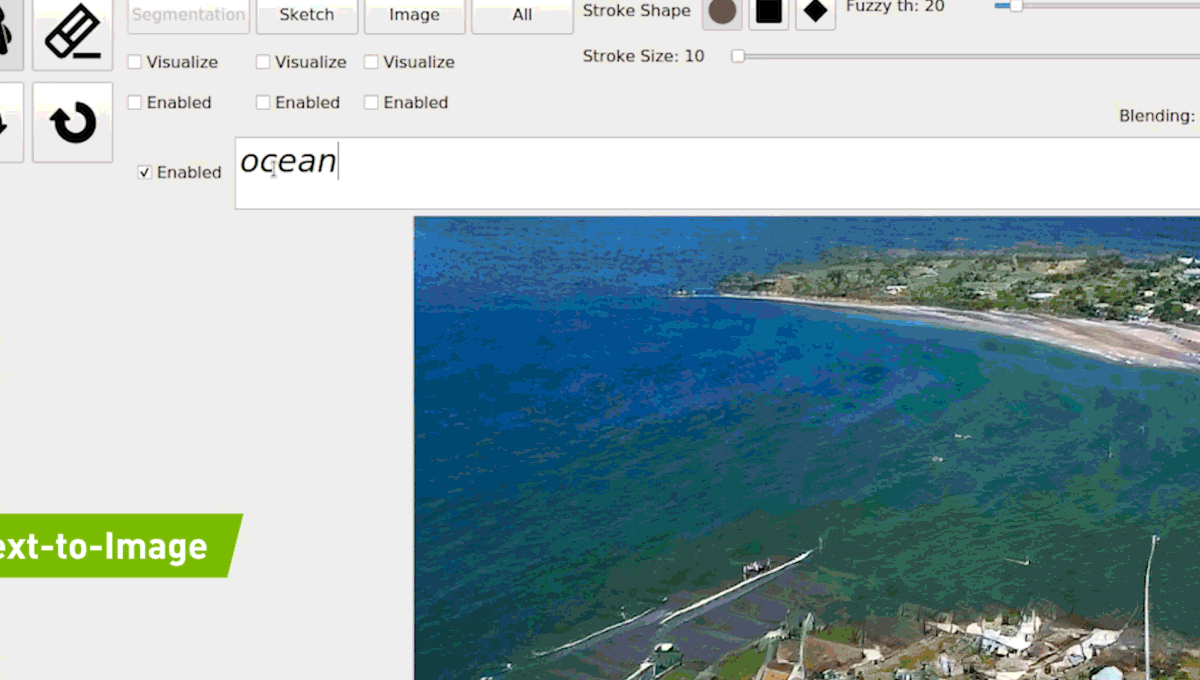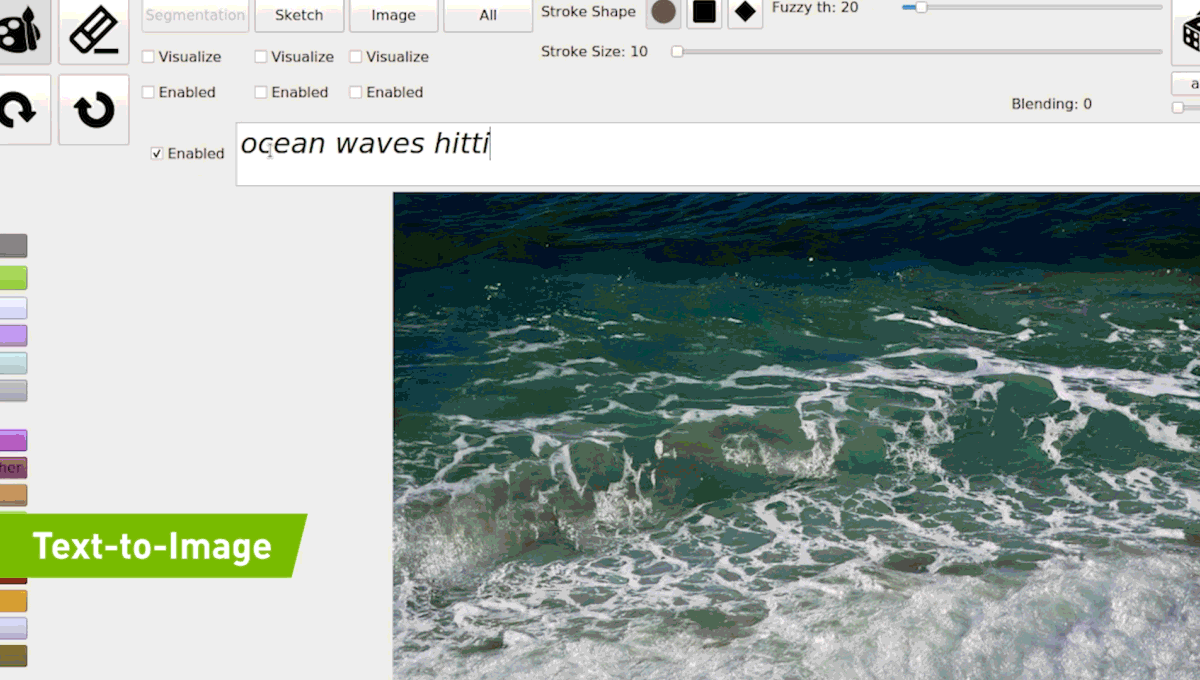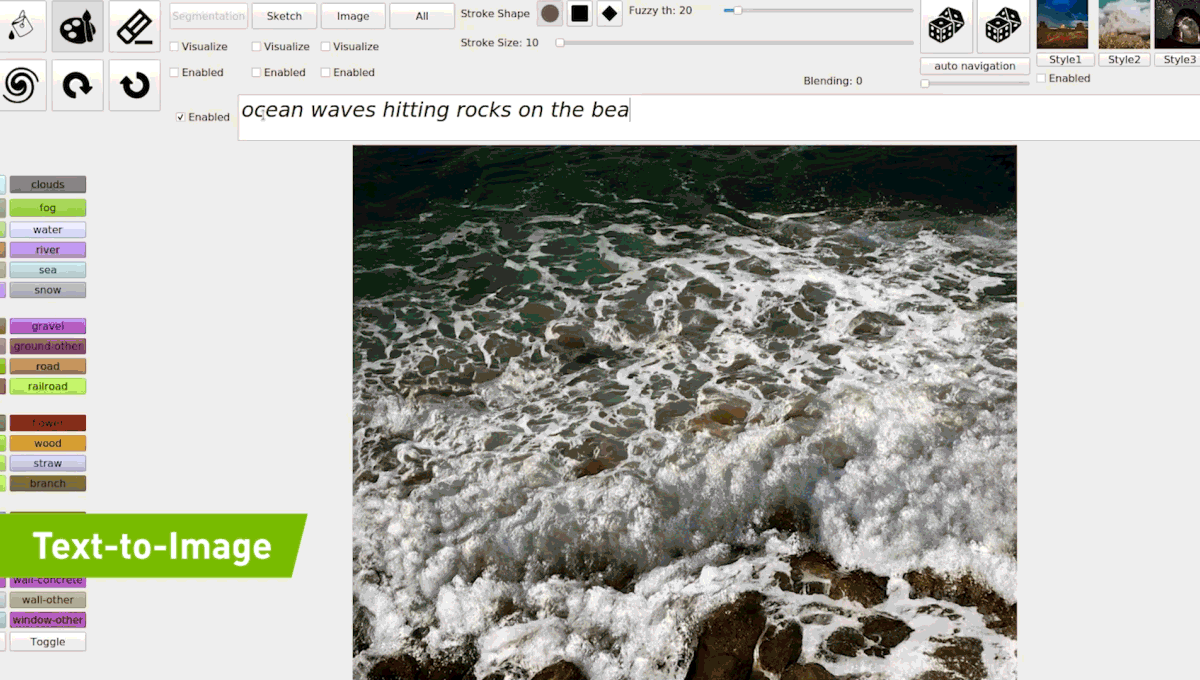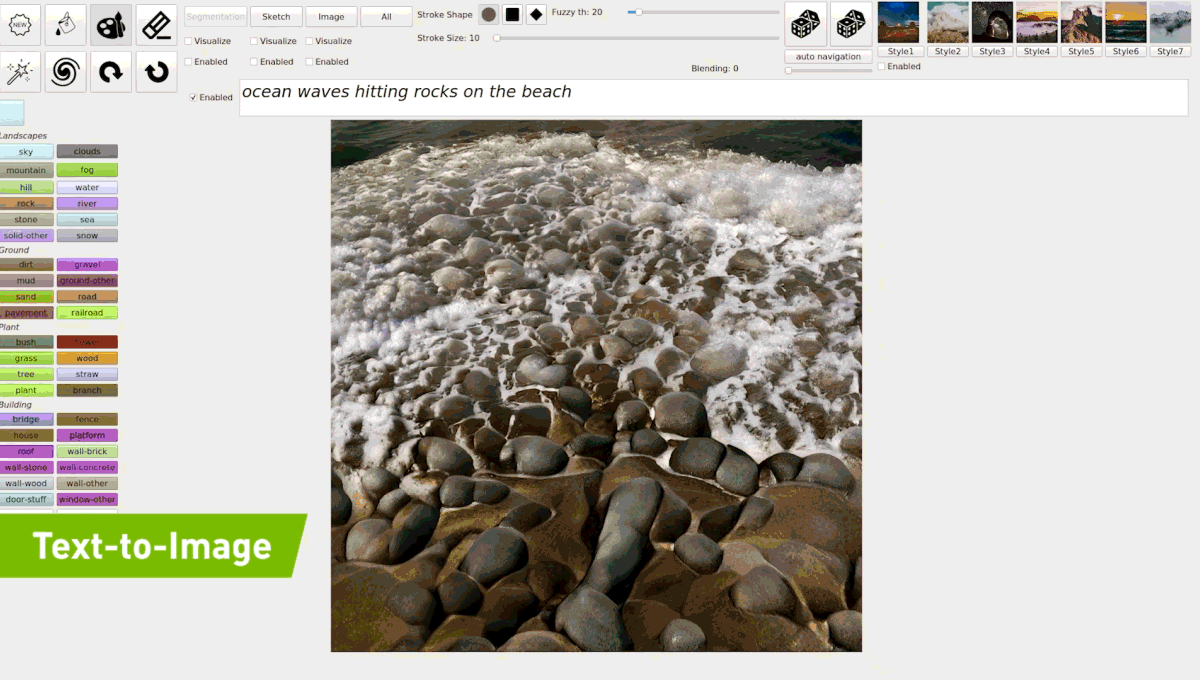
(2019) GauGAN
Source : https://syncedreview.com/2019/04/22/everyone-is-an-artist-gaugan-turns-doodles-into-photorealistic-landscapes/

(2021) GauGAN2
(2021) GLIDE

Novel View Synthesis of Static Content
(2020) NeRF
A super hot approach in neural rendering
(2018) Neural scene representation and rendering
The first article using notation "neural rendering"
Rendering a given scene from new camera positions, given a set of images and their camera poses as training set.
Generalization over Object and Scene Classes
With lesser training data/inputs.

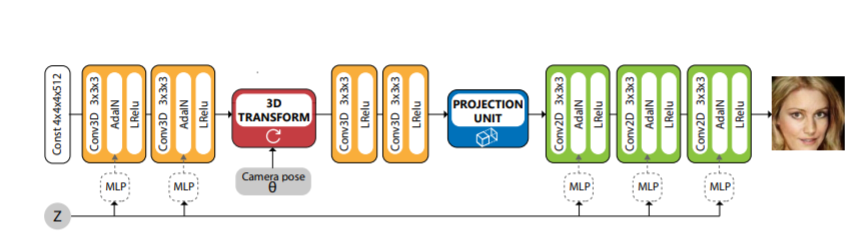



HoloGAN can train a GAN model with pure 2D training data
The key idea is apply 3D transform in 4D tensor (X,Y,Z,C).

(2021) IBRNet
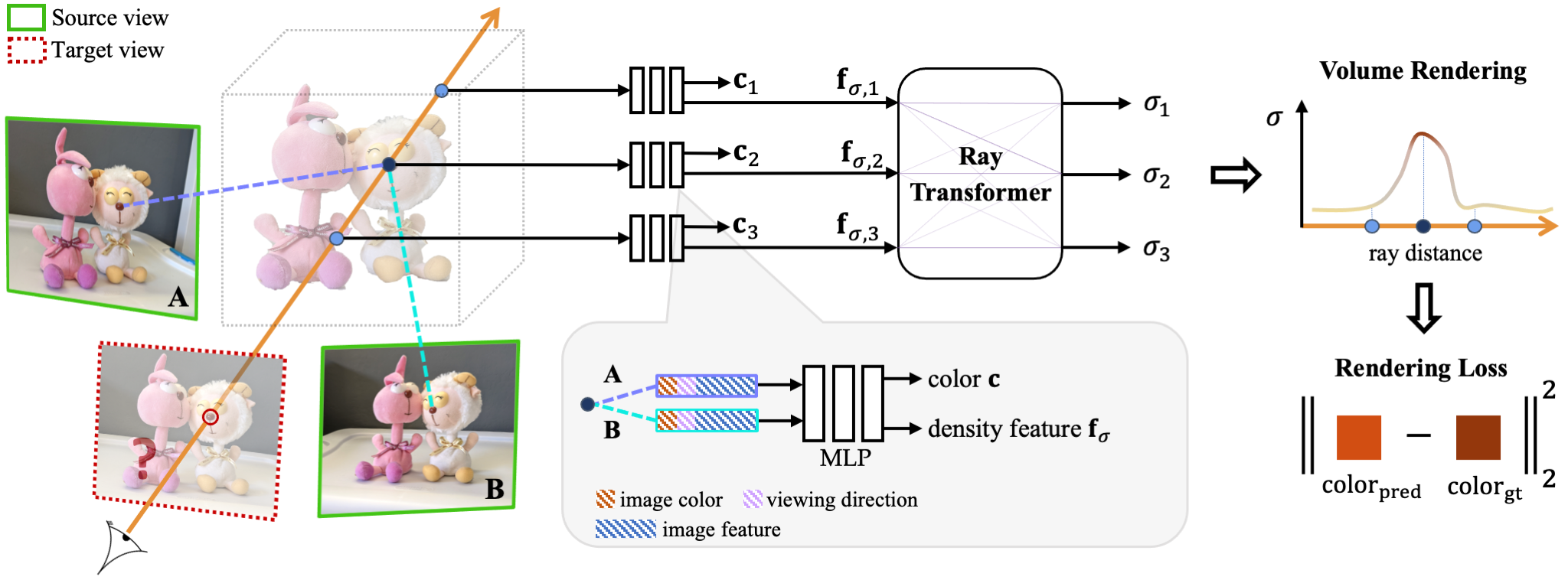

IBRNet rendering novel view based on the camera rays to other view points
Learning to Represent and Render Non-static Content
Handling dynamically changing content.

(1999) Bullet Time
Movie : The Matrix

(2020) non-rigid NeRF
Compositionality and Editing
Rearranging and affine transforming the objects and altering their structure and appearance.

(2021) Editing Conditional Radiance Fields
This method can propagate coarse 2D user scribbles to the 3D space, to modify the color or shape of a local region.
(2021) st-nerf
Enabling a variety of editing functions
manipulating the scale and location
duplicating
retiming
(2:28~End)
Relighting and Material Editing

(2021) Total Relighting
A novel system for portrait relighting and background replacement.
(2020) Real-time Deep Dynamic Characters
Using a human video to driving a given monocular RGB image.
(2:20:10~2:22:18)



(2021) Text2Mesh
Editing input mesh with "text" prompt or "image" prompt.
NeRF-Based Algorithms
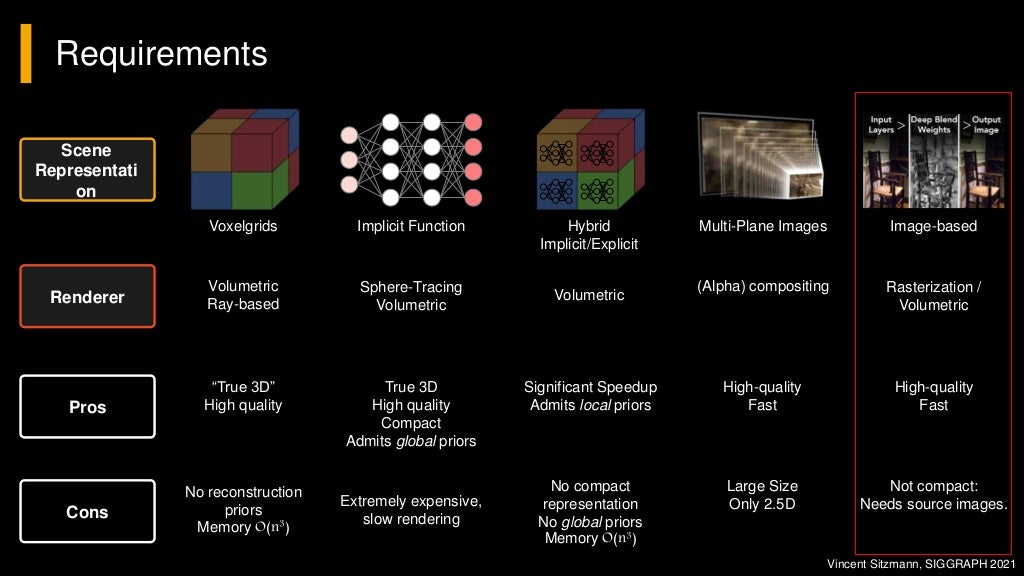
slide: link, video : https://youtu.be/otly9jcZ0Jg?t=4429
Approaches in Novel View Synthesis
NeRF Based Algorithms
- (Base) NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
- (Faster Inference) Neural Sparse Voxel Fields
- (Faster Training) Depth-supervised NeRF: Fewer Views and Faster Training for Free
- (Lighting) NeRV: Neural Reflectance and Visibility Fields
for Relighting and View Synthesis
All topics in awesome-NeRF : Faster Inference / Faster Training / Unconstrained Images / Deformable / Video / Generalization / Pose Estimation / Lighting / Compositionality / Scene Labelling and Understanding / Editing / Object Category Modeling / Multi-scale / Model Reconstruction / Depth Estimation
- Publish at arxiv 2003.08934 (2020 March)
- Cited by 749 at 2022 Feb
- Author Video Explain at SIGGRAPH 2021 Course
- Neural Volumetric Rendering
- 5D input : Spatial x,y,z + View Direction θ, ϕ
- Training data : 20~30 images (and their position, direction information)
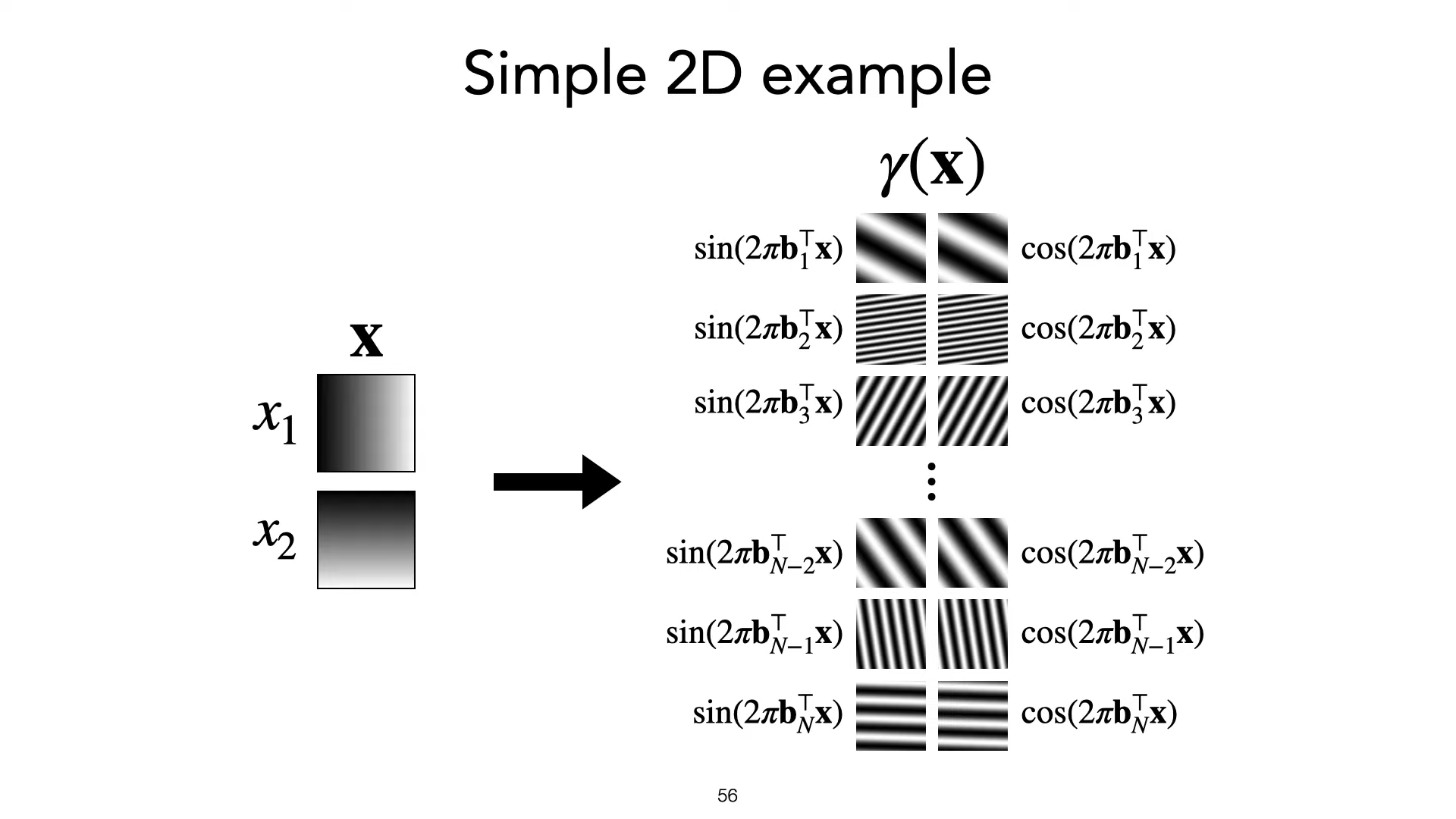
- Positional Encoding
- Neural model is a MLP Network (Not CNN or Transformer)
- Each of the follow scene is encoding into \(\approx\) 5 MB network
Source : https://www.matthewtancik.com/nerf







Idea

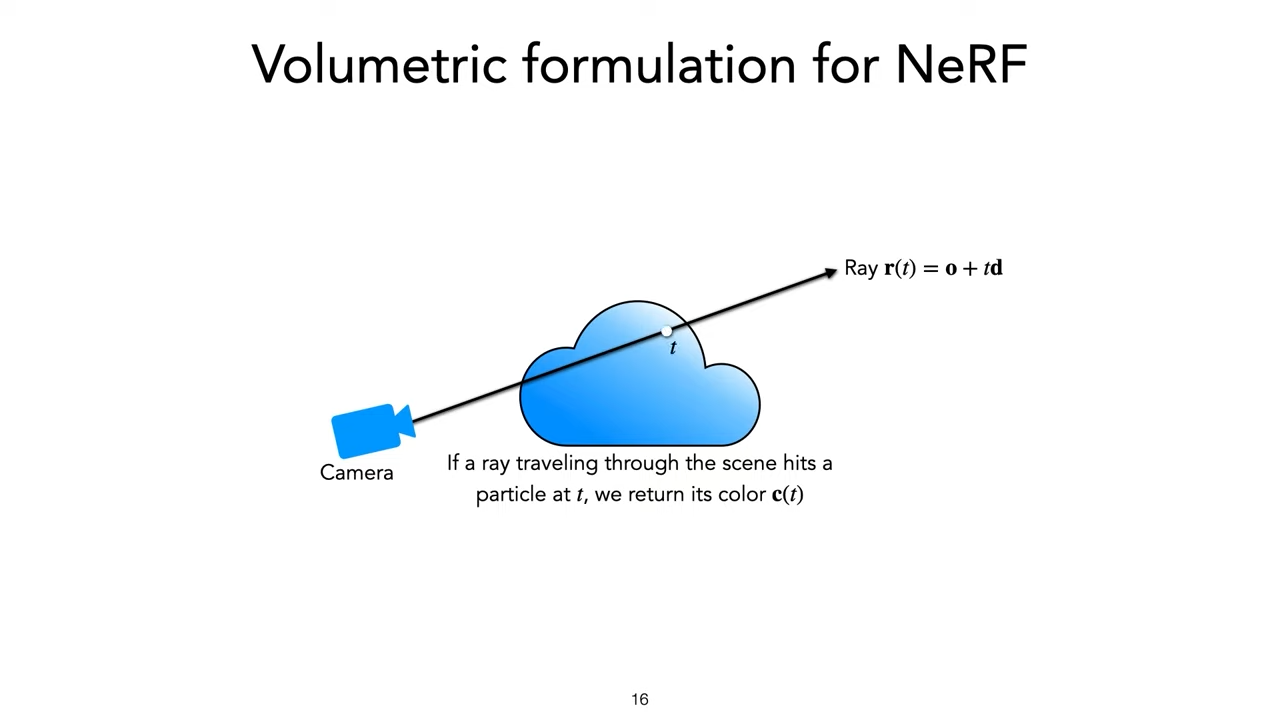
suppose we have
color \(c\)

volume density : \(\sigma(t)\)
suppose we have
color \(c\)
density \(\sigma\)

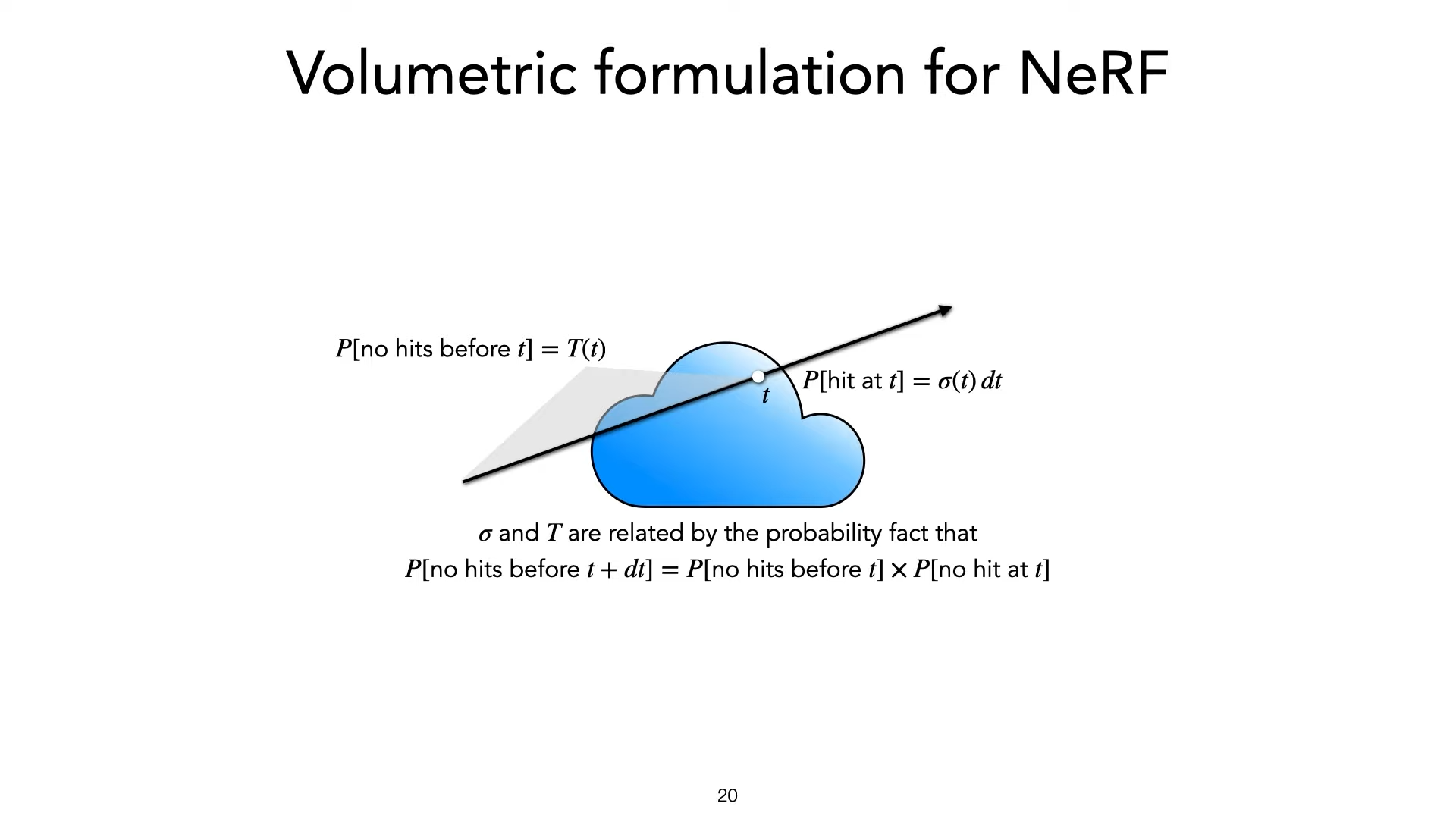
volume density : \(\sigma(t)\)
P[no hit before t] : \(T(t)\)
suppose we have
color \(c\)
density \(\sigma\)
volume density : \(\sigma(t)\)
P[no hit before t] : \(T(t)\)
suppose we have
color \(c\)
density \(\sigma\)

Some Math

volume density : \(\sigma(t)\)
P[no hit before t] : \(T(t)\)
\(=exp(-\int_{t_0}^{t}\sigma(s)ds)\)
suppose we have
color \(c\)
density \(\sigma\)

volume density : \(\sigma(t)\)
P[no hit before t] : \(T(t)\)
\(=exp(-\int_{t_0}^{t}\sigma(s)ds)\)
Probablity of first hit at \(t\) : \(T(t)\sigma(t)dt\)
suppose we have
color \(c\)
density \(\sigma\)
volume density : \(\sigma(t)\)
P[no hit before t] : \(T(t)\)
\(=exp(-\int_{t_0}^{t}\sigma(s)ds)\)
Probablity of first hit at \(t\) : \(T(t)\sigma(t)dt\)
expected color for ray :
\(\int_{t_0}^{t_1}T(t)\sigma(t)c(t)dt\)

suppose we have
color \(c\)
density \(\sigma\)
volume density : \(\sigma(t)\)
P[no hit before t] : \(T(t)\)
\(=exp(-\int_{t_0}^{t}\sigma(s)ds)\)
Probablity of first hit at \(t\) : \(T(t)\sigma(t)dt\)
expected color for ray :
\(\int_{t_0}^{t_1}T(t)\sigma(t)c(t)dt\)
\(\approx\) a lower computation term
\(=\sum_{i=1}^{n}T_i c_i \alpha_i\)



Some Math
suppose we have
color \(c\)
density \(\sigma\)
volume density : \(\sigma(t)\)
P[no hit before t] : \(T(t)\)
\(=exp(-\int_{t_0}^{t}\sigma(s)ds)\)
Probablity of first hit at \(t\) : \(T(t)\sigma(t)dt\)
expected color for ray :
\(\int_{t_0}^{t_1}T(t)\sigma(t)c(t)dt\)
\(\approx\) a lower computation term
\(=\sum_{i=1}^{n}T_i c_i \alpha_i\)
Notation for computation Detail:
\(T_i = \prod_{j=1}^{i-1} (1-\alpha_j)\)
\(\alpha_i = 1-exp(-\sigma_i\delta_i)\)

suppose we have
color \(c\)
density \(\sigma\)
- ✅ essential knowledge in traditional volume rendering
- ❎ particle function \(\sigma, c\) in the real world
volume density : \(\sigma(t)\)
P[no hit before t] : \(T(t)\)
\(=exp(-\int_{t_0}^{t}\sigma(s)ds)\)
Probablity of first hit at \(t\) : \(T(t)\sigma(t)dt\)
expected color for ray :
\(\int_{t_0}^{t_1}T(t)\sigma(t)c(t)dt\)
\(\approx\) a lower computation term
\(=\sum_{i=1}^{n}T_i c_i \alpha_i\)
Notation for computation Detail:
\(T_i = \prod_{j=1}^{i-1} (1-\alpha_j)\)
\(\alpha_i = 1-exp(-\sigma_i\delta_i)\)
suppose we have
color \(c\)
density \(\sigma\)
- ✅ essential knowledge in traditional volume rendering
- ❎ particle function \(\sigma, c\) in the real world
\( \rightarrow\) model them with a nerual network
volume density : \(\sigma(t)\)
P[no hit before t] : \(T(t)\)
\(=exp(-\int_{t_0}^{t}\sigma(s)ds)\)
Probablity of first hit at \(t\) : \(T(t)\sigma(t)dt\)
expected color for ray :
\(\int_{t_0}^{t_1}T(t)\sigma(t)c(t)dt\)
\(\approx\) a lower computation term
\(=\sum_{i=1}^{n}T_i c_i \alpha_i\)
Notation for computation Detail:
\(T_i = \prod_{j=1}^{i-1} (1-\alpha_j)\)
\(\alpha_i = 1-exp(-\sigma_i\delta_i)\)
Estimated
color \(c\)
density \(\sigma\)

Store Data Approaches

(x,y)
\(\mathcal{O}(n^2)\)
\(\mathcal{O}(p)\)
(x,y) \(\rightarrow\) r,g,b
\(r,g,b = A[x,y]\)
\(r,g,b = f(x,y)\)
Matrix
MLP Network
Necessary information for get color of a particle
[particle denstiy \(\sigma\) and color \(r,g,b\)]
depends on
spatial information & view direction
\((x, y, z, \theta, \phi)\)

Store Data Approaches

(x,y)
\(\mathcal{O}(n^2)\)
\(\mathcal{O}(p)\)
\((x, y, z, \theta, \phi)\)
\(\rightarrow r,g,b,\sigma\)

\(r,g,b,\sigma = A[x, y, z, \theta, \phi]\)
\(\mathcal{O}(n^5)\)
Matrix
MLP Network
\(r,g,b,\sigma = f(x, y, z, \theta, \phi)\)
\(\mathcal{O}(p)\)
(x,y) \(\rightarrow\) r,g,b
\(r,g,b = A[x,y]\)
\(r,g,b = f(x,y)\)








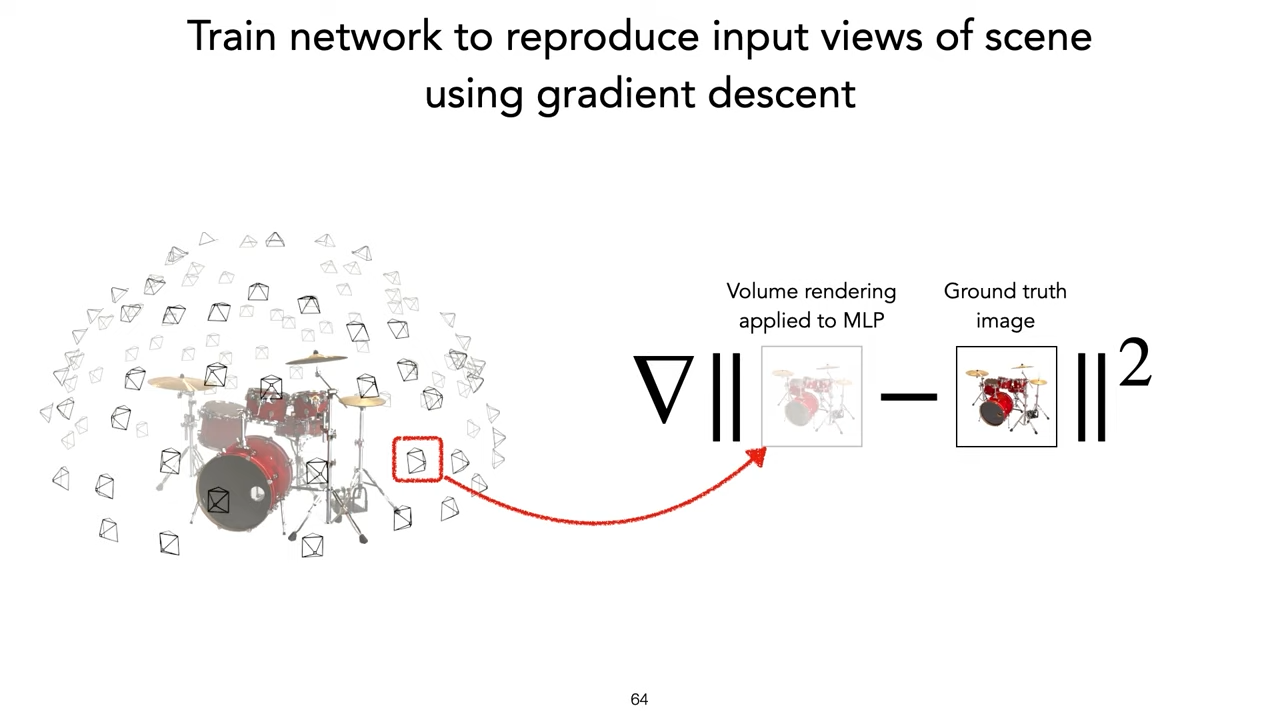
\(argmin_{MLP}(\sum_{i=1}^{n}T_i c_i \alpha_i - c_{true})^2\)

A very nice way to connect traditional and modern techniques
And can insert lots of technique easily
\(argmin_{MLP}(\sum_{i=1}^{n}T_i c_i \alpha_i - c_{true})^2\)
NeRF problems
- Not anti-alised
- Very slow
- Network must be retrained for every scene
- Requires many input images
- Need scene to be static and have fixed lighting
NeRF website
- Publish at arxiv 2007.11571 (2020 July)
- Cited by 173 at 2022 Feb
- Author Video Explain at SIGGRAPH 2021 Course
Key Idea : Split a global MLP to sparse voxel wise MLP
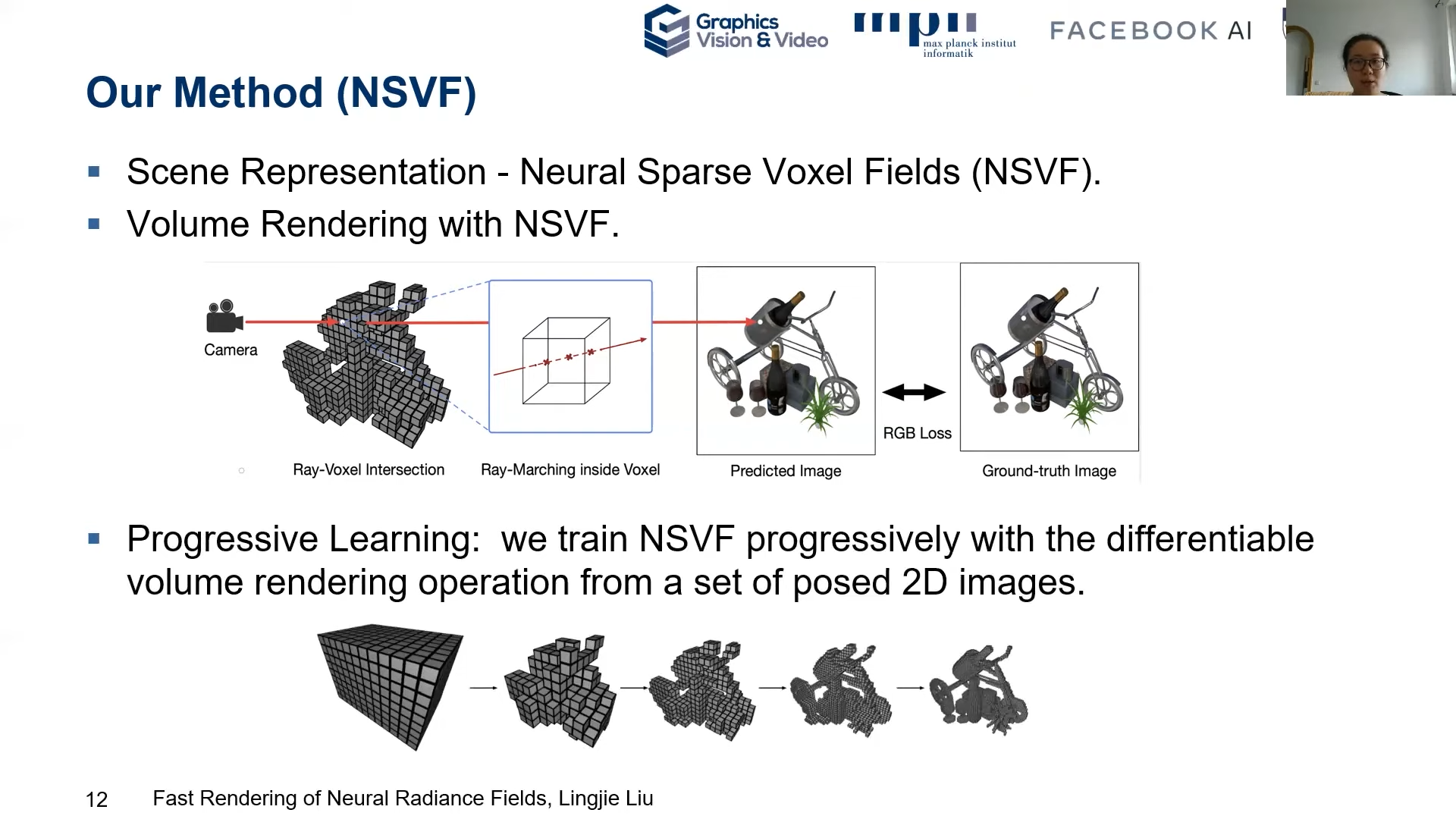
- Publish at arxiv 2007.11571 (2020 July)
- Cited by 173 at 2022 Feb
- Author Video Explain at SIGGRAPH 2021 Course
Key Idea : Split a global MLP to sparse voxel wise MLP
Advantages :
- More powerful in finer detail
- Much faster than NeRF

- Publish at arxiv 2007.11571 (2020 July)
- Cited by 173 at 2022 Feb
- Author Video Explain at SIGGRAPH 2021 Course
Key Idea : Split a global MLP to sparse voxel wise MLP
Advantages :
- More powerful in finer detail
- Much faster than NeRF
- Easily Scene editing and composition
(Since model with voxel wise MLP explicitly)
- Publish at arxiv 2107.02791 (2021 July)
- Cited by 14 at 2022 Feb
- Author Video Explain at project page
Their method can train NeRF with fewer input and faster
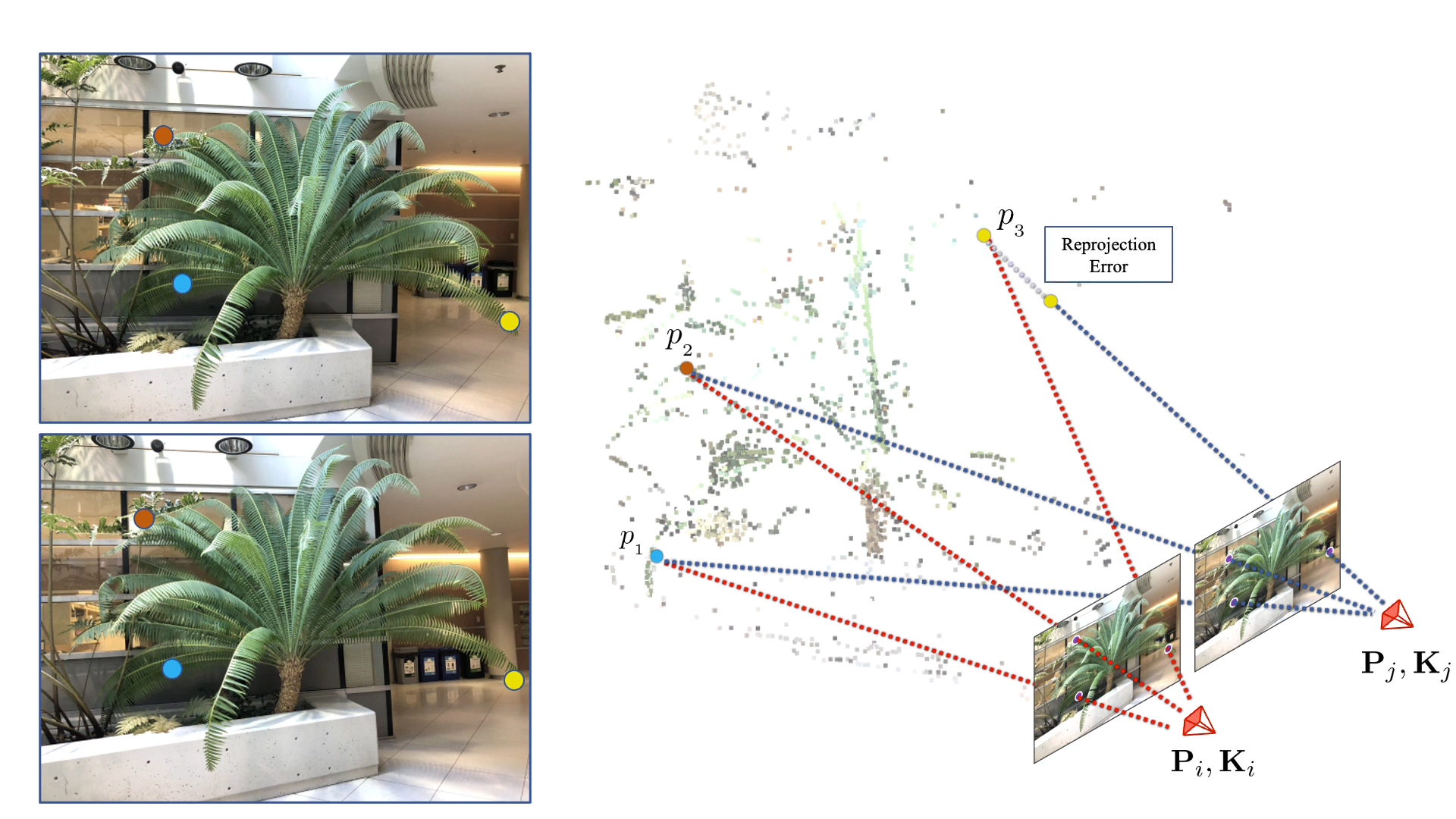
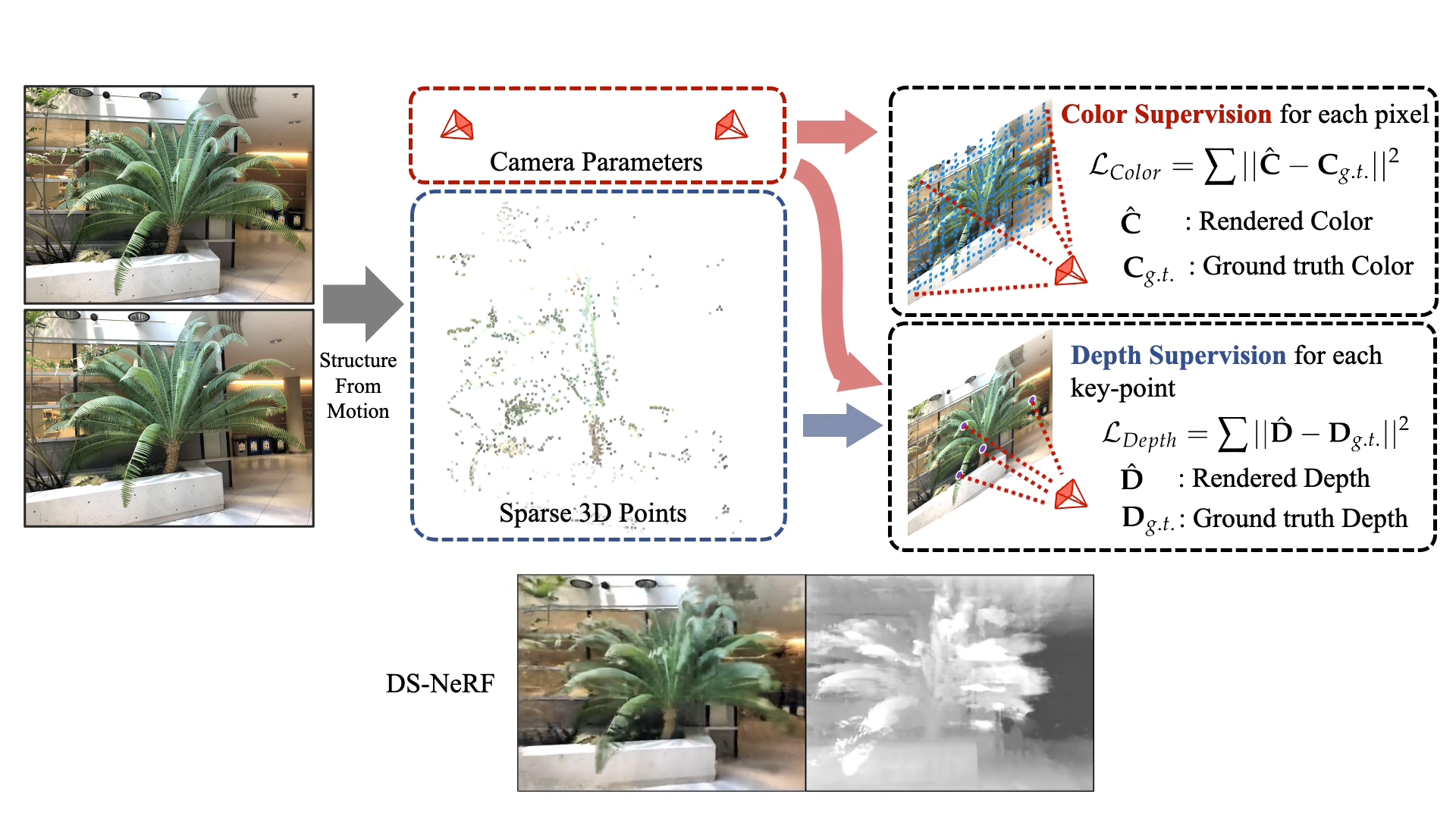
Credit : http://www.cs.cmu.edu/~dsnerf/




RGB
Depth
NeRF
DS-NeRF
NeRF
DS-NeRF
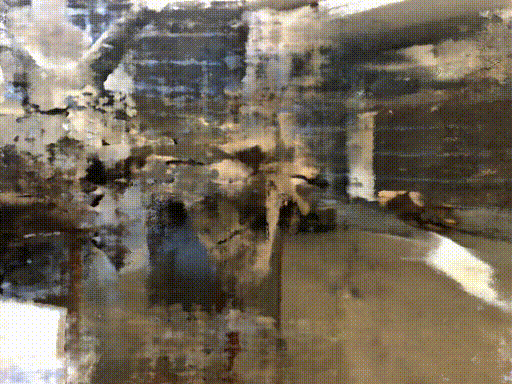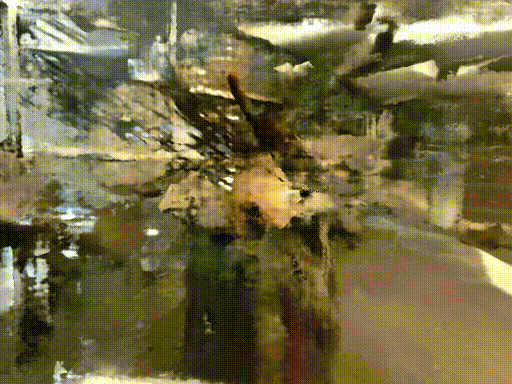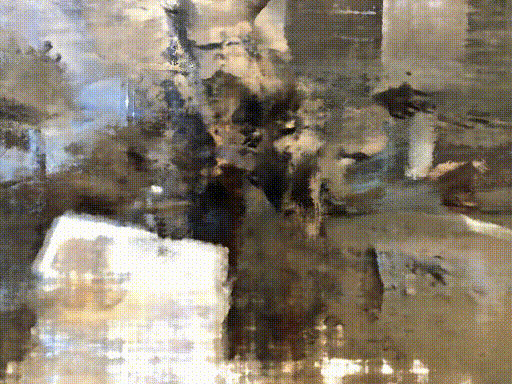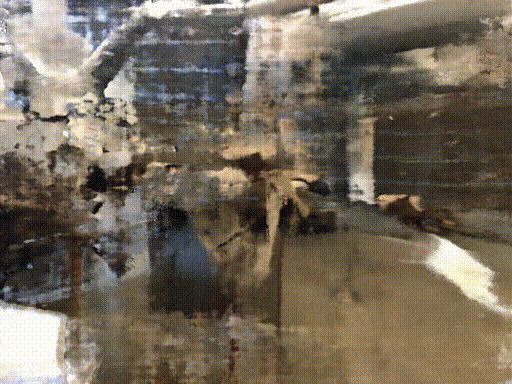



All of following result train with 2 input
- Publish at arxiv 2107.02791 (2021 July)
- Cited by 14 at 2022 Feb
- Author Video Explain at project page
Their method can train NeRF with fewer input and faster
Key Idea :
Free lunch from depth estimation of key points
- Publish at arxiv 2107.02791 (2021 July)
- Cited by 14 at 2022 Feb
- Author Video Explain at project page
Their method can train NeRF with fewer input and faster
Key Idea :
Free lunch from depth estimation of key points
Supervise it!
- Publish at arxiv 2012.03927 (2020 Dec)
- Cited by 70 at 2022 Feb
- Author Video Explain at project page
Additional : Known light source in training
Relighting and View Synthesis
Material Editing
Relighting and View Synthesis
Material Editing
- Publish at arxiv 2012.03927 (2020 Dec)
- Cited by 70 at 2022 Feb
- Author Video Explain at project page
Additional : Known light source in training
Relighting and View Synthesis
Material Editing
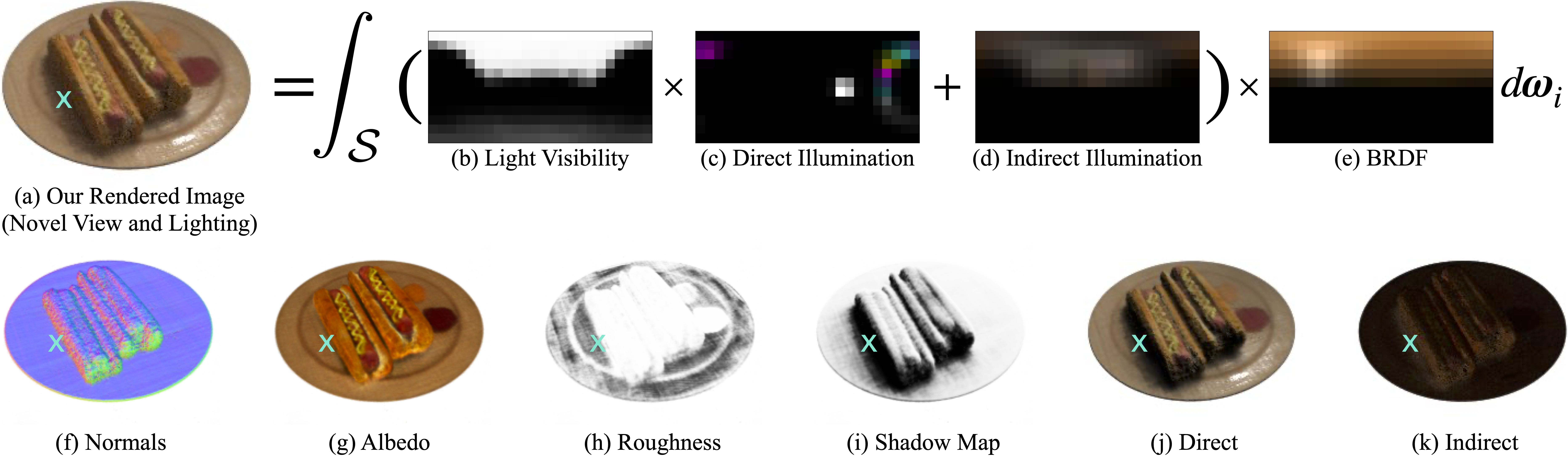
NeRF
Particles absorb enviorment light, then self emitting
NeRV

Phantom Blood
Prev :
won't use traditional techniques

Phantom Blood
After :
won't ignore CS history
Prev :
won't use traditional techniques
arxiv 2112.03221
Before Text2Mesh
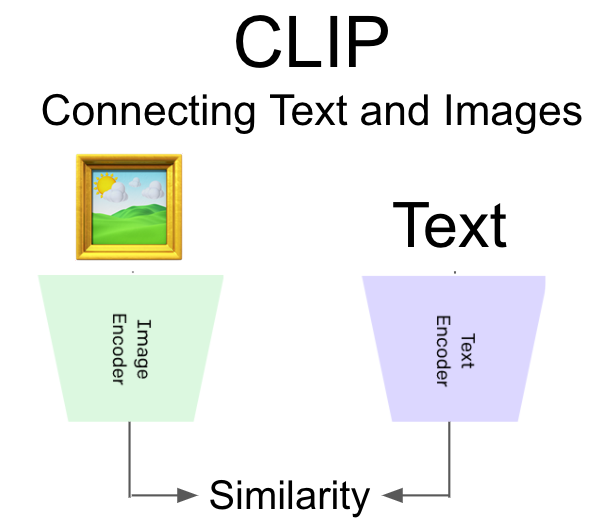
What is CLIP
OpenAI's model : CLIP
This model can measure the similarity between
(text, Image) pair
Awesome CLIP applications






Awesome CLIP applications



Awesome CLIP applications




-0.2
0.4
0.3
\(\cdots\)
\(\cdots\)


(Detic) Detecting Twenty-thousand Classes using Image-level Supervision
arXiv 2201.02605, github
Direct fuse some CLIP text information to training loop


Awesome CLIP applications

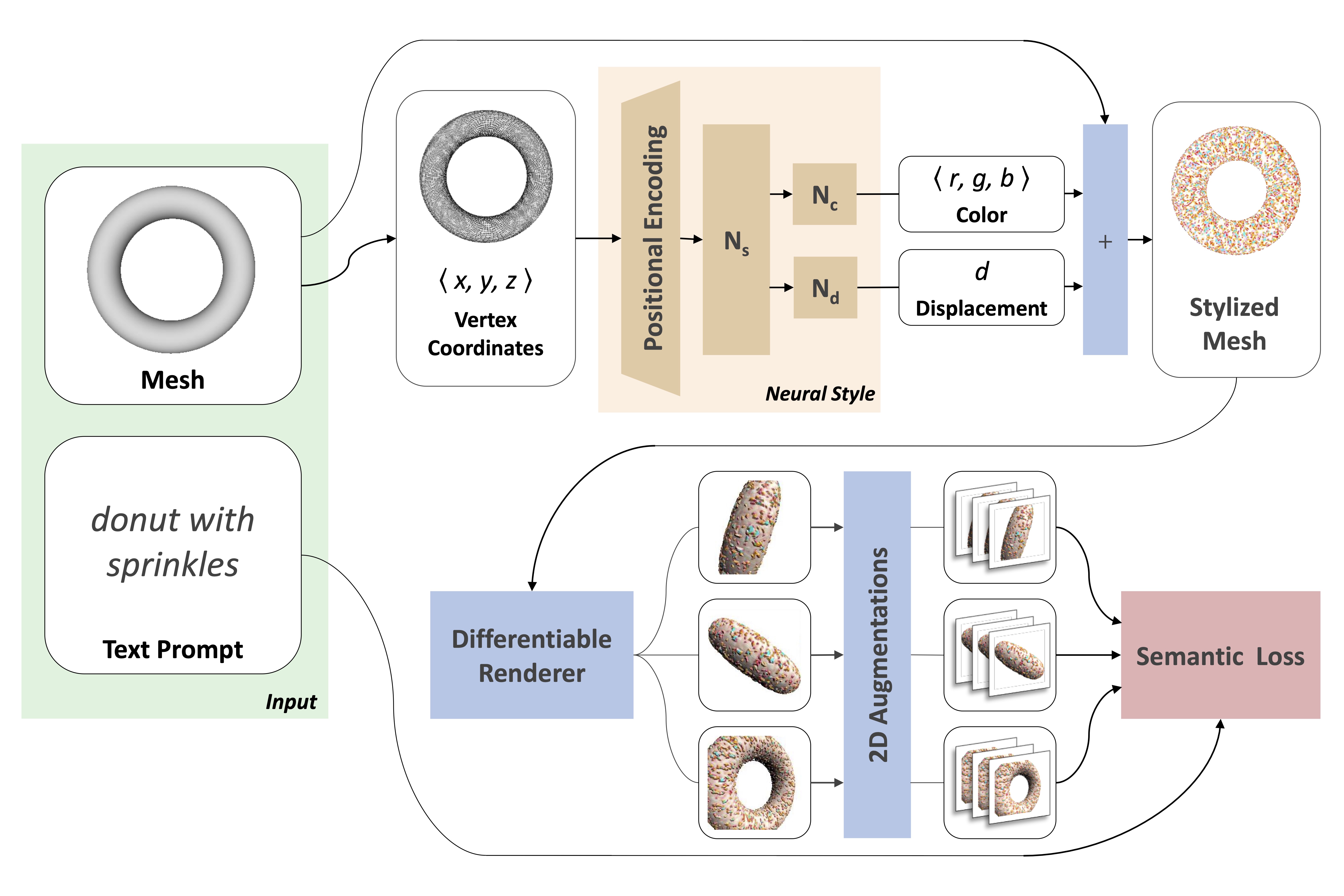
Text2Mesh modifies an input mesh to conform to the target text by predicting color and geometric details. The weights of the neural style network are optimized by rendering multiple 2D images and applying 2D augmentations, which are given a similarity score to the target from the CLIP-based semantic loss.
Text2Mesh

Edit the given mesh with a trainable MLP
The MLP\((x,y,z)\)
- color : \(<r,g,b>\)
- normal displacement : \(d\)

Select Images collection

Global

Local




Local
Displ

Augmentation
aug_x = transforms.RandomPerspective(
fill=1, p=0.8, distortion_scale=0.5
)(x.repaet(n,1,1,1))Total Loss
code_x = CLIP_I(aug_x)
avg_code_x = code_x.mean(axis=batch)
loss_x = -cos(avg_code_x, code_text)
total_loss = ( loss_global
+ loss_local + loss_displ)Ablations

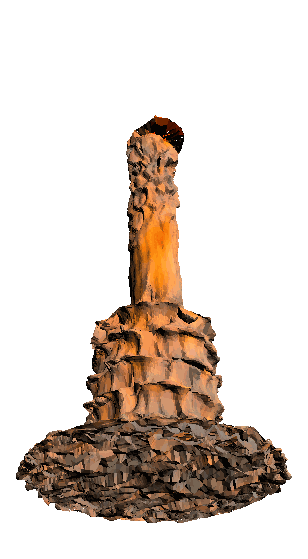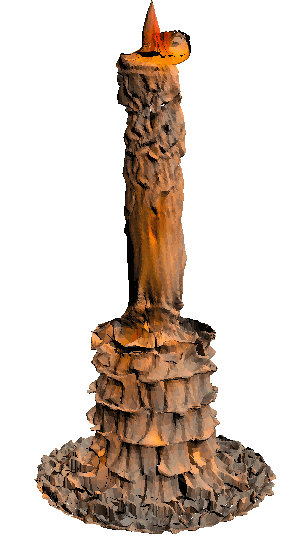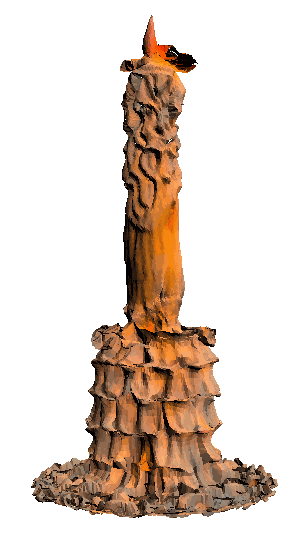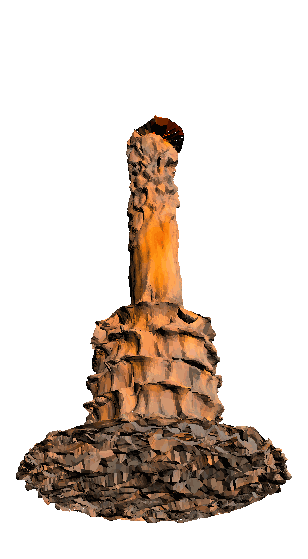

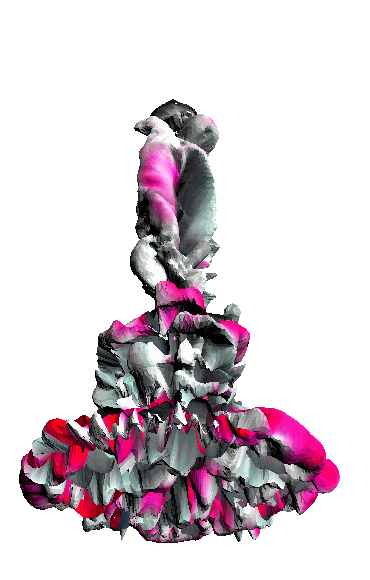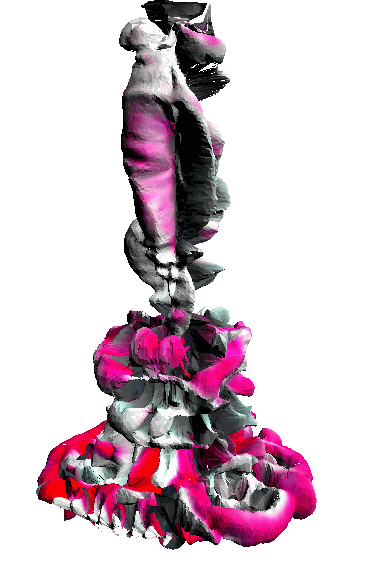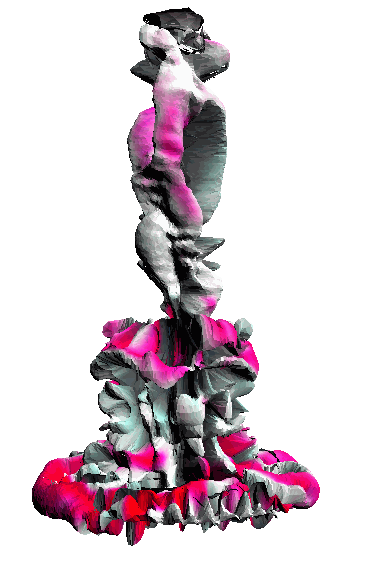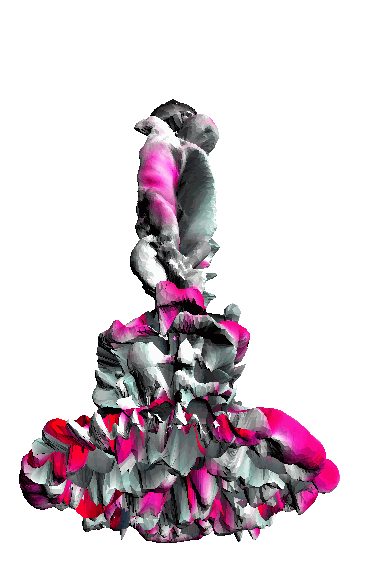

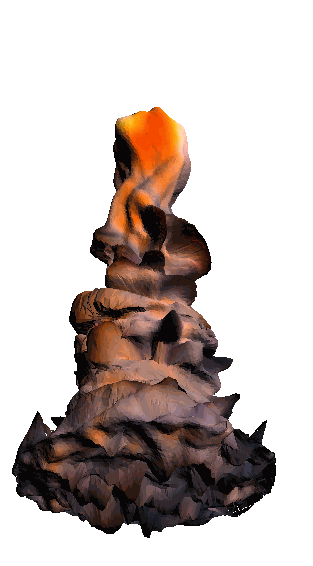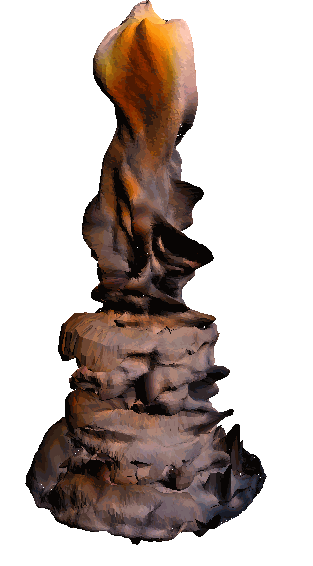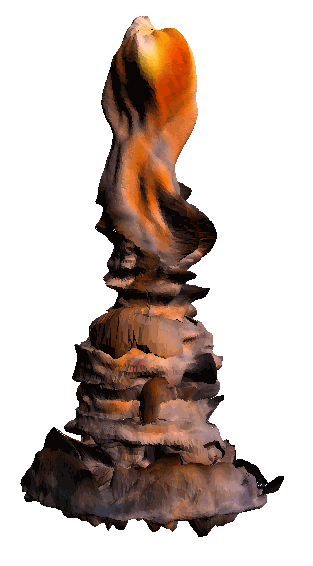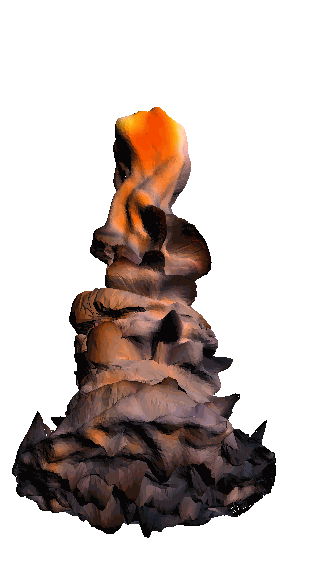


- - net : w/o network
- - aug : w/o augmentation
- - FFN : w/o position encoding
- - crop : w/o local
- - displ : w/o geometry-only
- - 3D : learning over 2D plane
‘Candle made of bark’
Beyond Text-Driven Manipulation




original target is \(CLIP_{Text}("...")\)
Can also use \(CLIP_{Image}(I)\) and get good result
Donald John Trump
My Experiments (~20 min/750 iter with colab pro)
based on this kaggle kernel : https://www.kaggle.com/neverix/text2mesh/
Nike Sport Shoe
Takeaway
- Neural Rendering is a booming research topic
- NeRF (2020 March) is a superhot bone method
- End-to-End
- Render with pure CG technique (Volumetric Rendering)
- Model the volumetric property with pure MLP
- Many research extend this bone method for different aspect
- You can get free lunch if you combine some modern / classical techniques in the wise way
- DS-NeRF
- Crop-CLIP
- There are some greedy (and work) techique for combine 2D and 3D information
- Text2Mesh
- Holo-GAN (advance : \(\pi\)-GAN)
- For advance, please goto Advances in Neural Rendering
Resources

Thanks
Feel free to send email to me
changethewhat+talk@gmail.com