Photonic crystal

Implémentation

Géométrie hexagonale

%The variable a defines the period of the structure.
%It influences on results in case of the frequency
%normalization.
a=1e-6; % in meters

%The variable r contains elements radius. Here it is
%defined as a part of the period.
r=0.4*a; % in meters

%The variable eps1 contains the information about
%the relative background material permittivity.
eps1=8.46;

%The variable eps2 contains the information about
%permittivity of the elements composing PhC. In our
%case permittivities are set to form the structure
%perforated membrane
eps2=1;

%Defining the coordinates of the high-symmetry point lattice in
        %reciprocal coordinates
        % Gamma
        Gx = 0;
        Gy = 0;
        
        % M
        Mx = pi/sqrt(a);
        My = -pi/(sqrt(3)*a);
        
        % K
        Kx = 4*pi/(3*a);
        Ky = 0;
        
        %Path GM
        kx(1:precis+1)=linspace(Gx,Mx,precis+1); 
        ky(1:precis+1)=linspace(Gy,My,precis+1); 
        
        %Path MK
        kx(precis+1:2*precis)=linspace(Mx,Kx,precis); 
        ky(precis+1:2*precis)=linspace(My,Ky,precis); 
        
        %Path KG
        kx(2*precis-1:3*precis-2)=linspace(Kx,Gx,precis); 
        ky(2*precis-1:3*precis-2)=linspace(Ky,Gy,precis);

Paramètres

Résultats

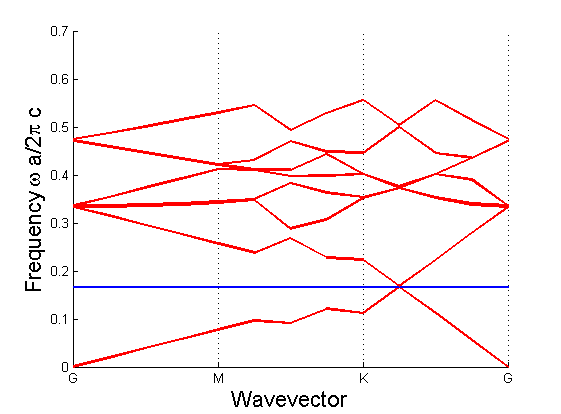
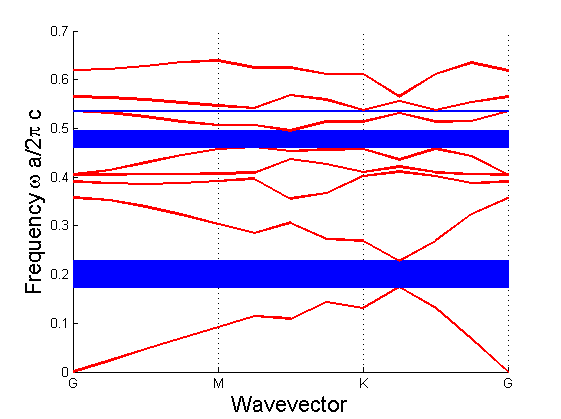
r / a = 0.01

r / a = 0.25

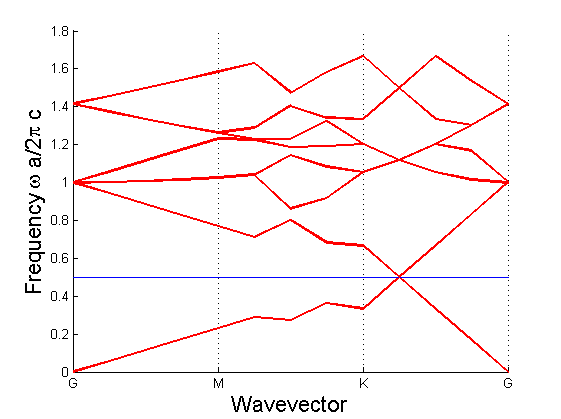
r / a = 0.9

Les figures précédentes montrent que le gap connaît une croissance avec la variation du rapport trou/cylindre entre 0 et 1.

Discussion

La croissance entre 0 et la valeur maximale s'explique intuitivement par la transition entre un milieu uniforme et la périodisation bi-dimensionnelle

La décroissance, elle, s'explique peut-être par une diminution de l'indice effectif rendant le cristal plus multimode.