Electromagnetic modeling of micro-nano-structured surfaces
Maximization of surface absorption
Comment j'ai fait ?
Un peu de théorie
Estimation de l'effet Joule
$$ P_{Joule} = \int_0^{t_{max}} \frac{1}{2} \sigma E^2 dt $$
$$ \sim \sum_{k=0}^{t_{max}} \left (\frac{1}{2} \sigma E_k^2 \cdot \delta t \right)$$
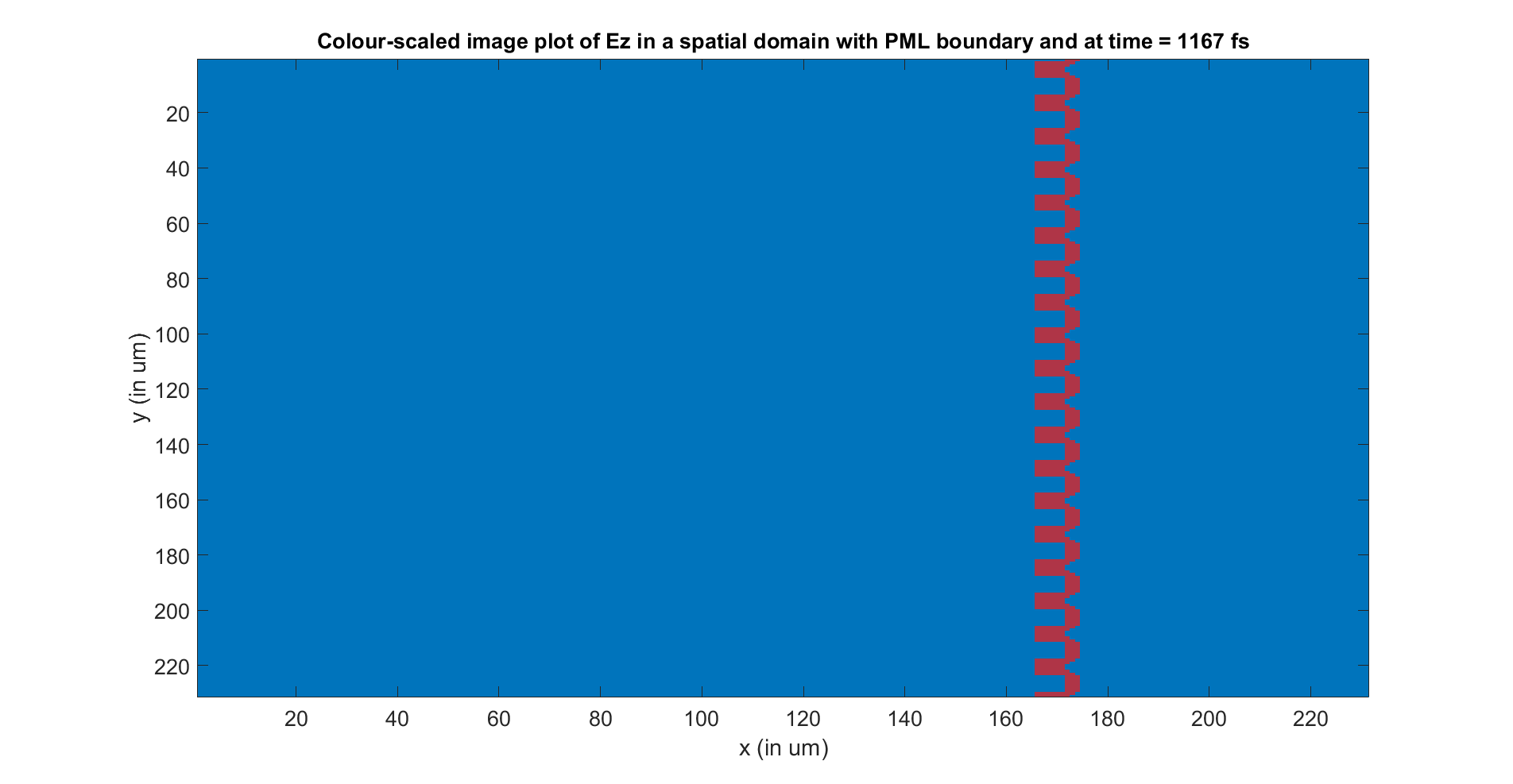
Ma géométrie
Cliquez sur l'image pour voir l'implémentation
Variation de la profondeur

| a | b | $t_m$ | E_f |
|---|---|---|---|
| 6 | 12 | 1400 | 3,00E-56 |
| 6 | 24 | 2357 | 9,84E-55 |
| 6 | 48 | 3500 | 1,00E-54 |
\(t_m\) : le temps pour que le système arrive à équilibre
\(E_f\) : l'énergie maximum présente dans le système
Variation de la largeur

| a | b | tm | Ef |
|---|---|---|---|
| 6 | 6 | 1160 | 1E-56 |
| 12 | 6 | 830 | 1,80E-56 |
| 48 | 6 | 790 | 8,40E-56 |
Résultats
Canal long
\longrightarrow
Couplage plus long
Plus de surface
\longrightarrow
Plus d'énergie
Conclusion
Géométrie fractale !