Data structures in JS
Maurizio Lupo @sithmel
I suppose it is tempting, if the only tool you have is a hammer, to treat everything as if it were a nail
Abraham Maslow
They are tools to map relations between data
some operation is fast/convenient
Some other is slow/cumbersome
Arrays
✓ Indexed
✓ Sorted
Objects/Maps/Sets
✓ Key/value
✓ Unsorted*
Fast:
It scales well when more items are involved
Big OH notation
O(n)
O(n log n)
...
O(n²)
Big OH notation
Only for:
Big numbers
Worst possible scenario
Big OH notation
4+5n²
n²
This one doesn't make sense
This one does
Big OH notation
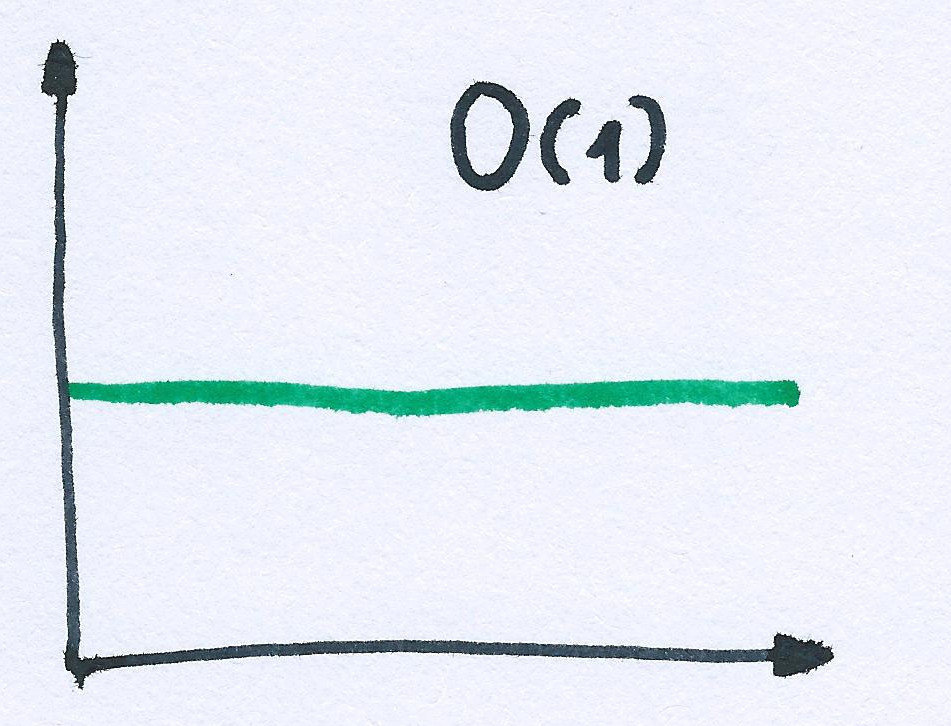
obj.foo = 'bar';
arr[2] = 10;
Big OH notation
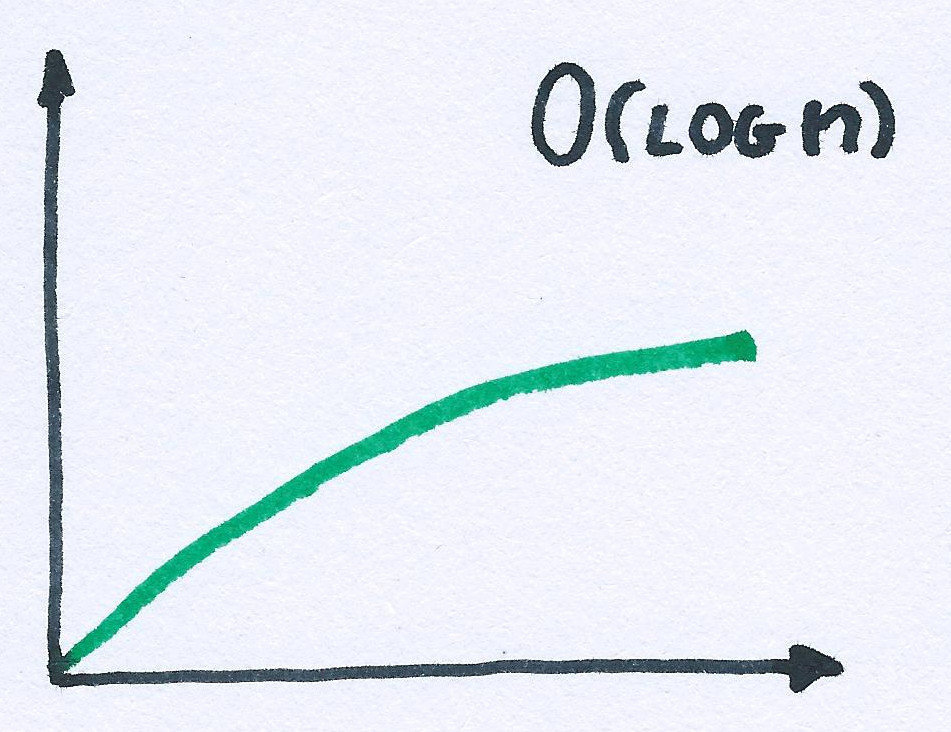
// binary search
_.sortedIndexOf(sortedArray, value)Logarithmic growth (log base 2)
4 => 2
8 => 3
16 => 4
65536 => 16
number of items => number of operations
Big OH notation

unsortedArray.indexOf(value);
array.shift();Linear algorithm
function sum(...numbers) {
let total = 0
for (const n of numbers) {
total += n
}
return total
}
sum(1, 2, 3)
sum(1, 2, 3, 4, 5, 6) // this takes twiceBig OH notation
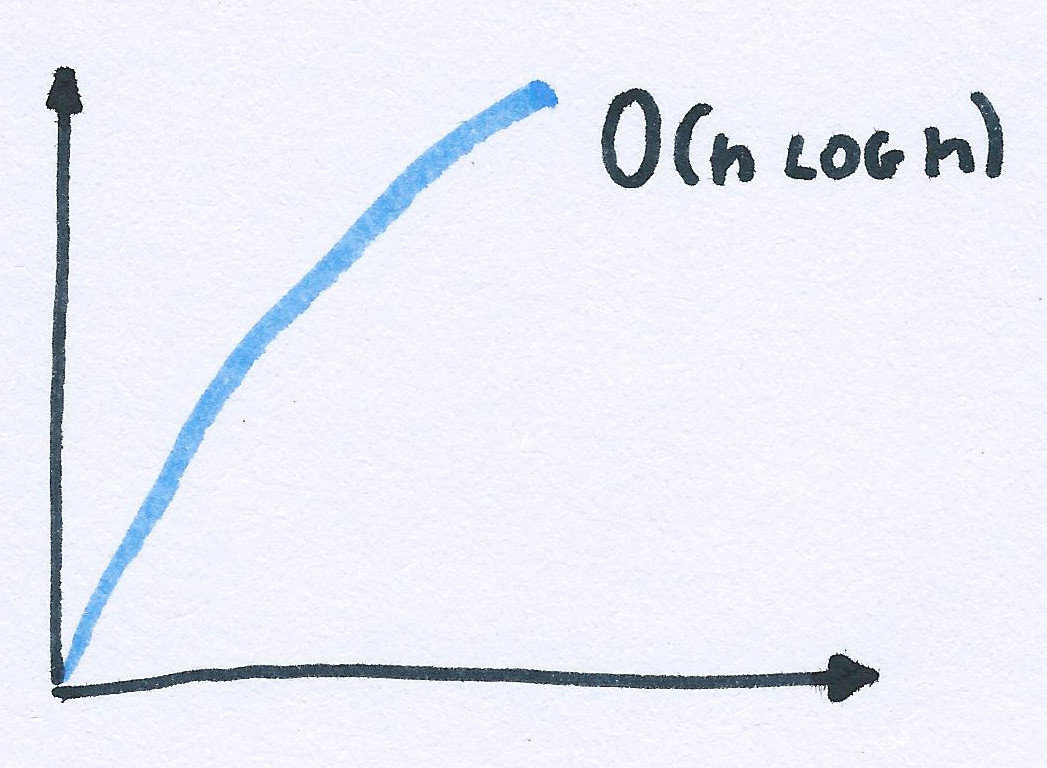
array.sort();Big OH notation
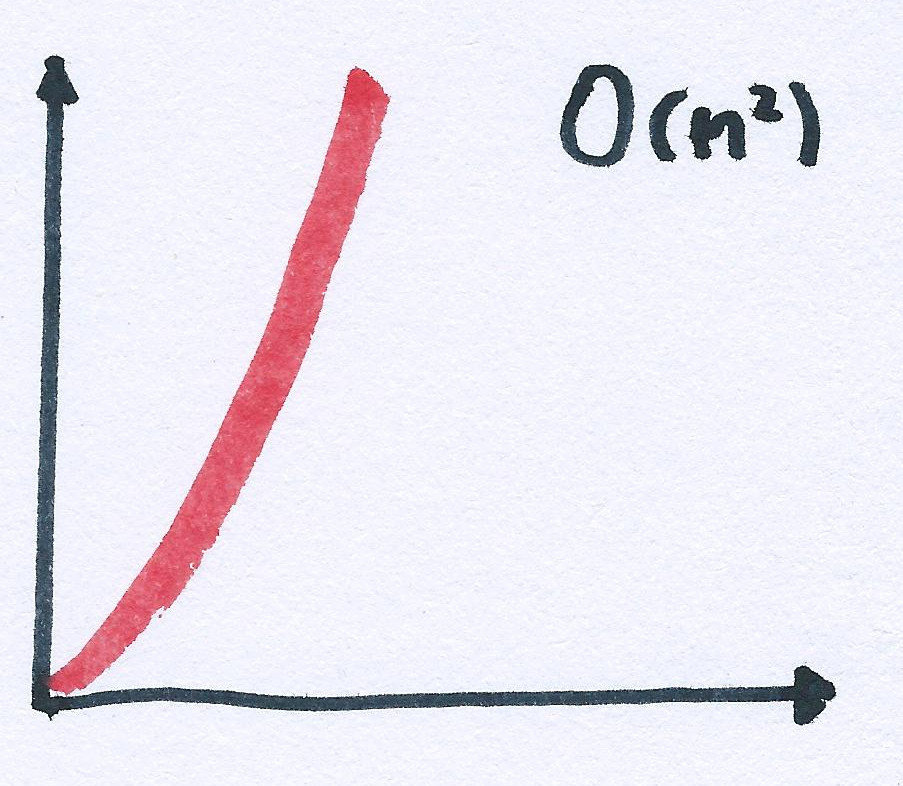
const cards = [...]
const pairs = []
for (const firstCard of cards) {
for (const secondCard of cards) {
if (firstCard !== secondCard) {
pairs.push([firstCard, secondCard])
}
}
}JS data structures: arrays
- access with known index O(1)
- indexOf/find/includes O(n)
- sort O(n log n)
- splice/slice O(n)
- push/pop O(1) *
- shift/unshift O(n)
JS data structures: objects
- access with known key O(1)
- adding a new item O(1)
- unsorted *
and ES6 Maps and Sets
Are they enough?
No
They are building blocks
Example:
Priority queue
Operations:
getMax: get the maximum
push: add a new item
Using an array
getMax O(n log n)
push O(1)
arr.push(item);arr.sort((a, b) => a - b).pop();Using an array (2)
getMax O(1)
push O(n)
const i = _.sortedIndex(sortedArray, item); // O(log n)
sortedArray.splice(i, 0, item); // O(n)arr.pop();Heap
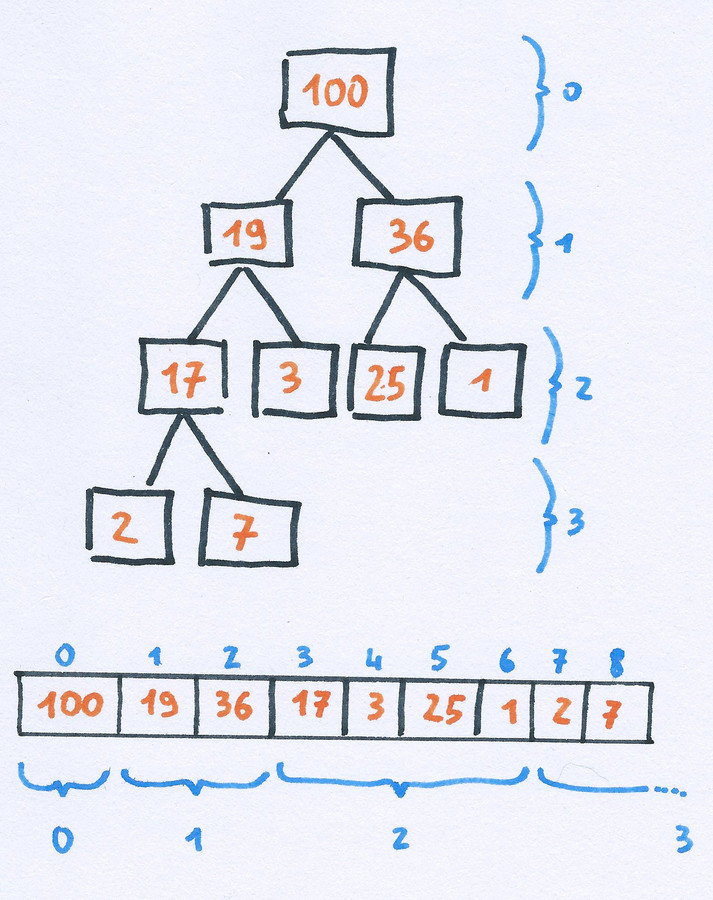
Heap
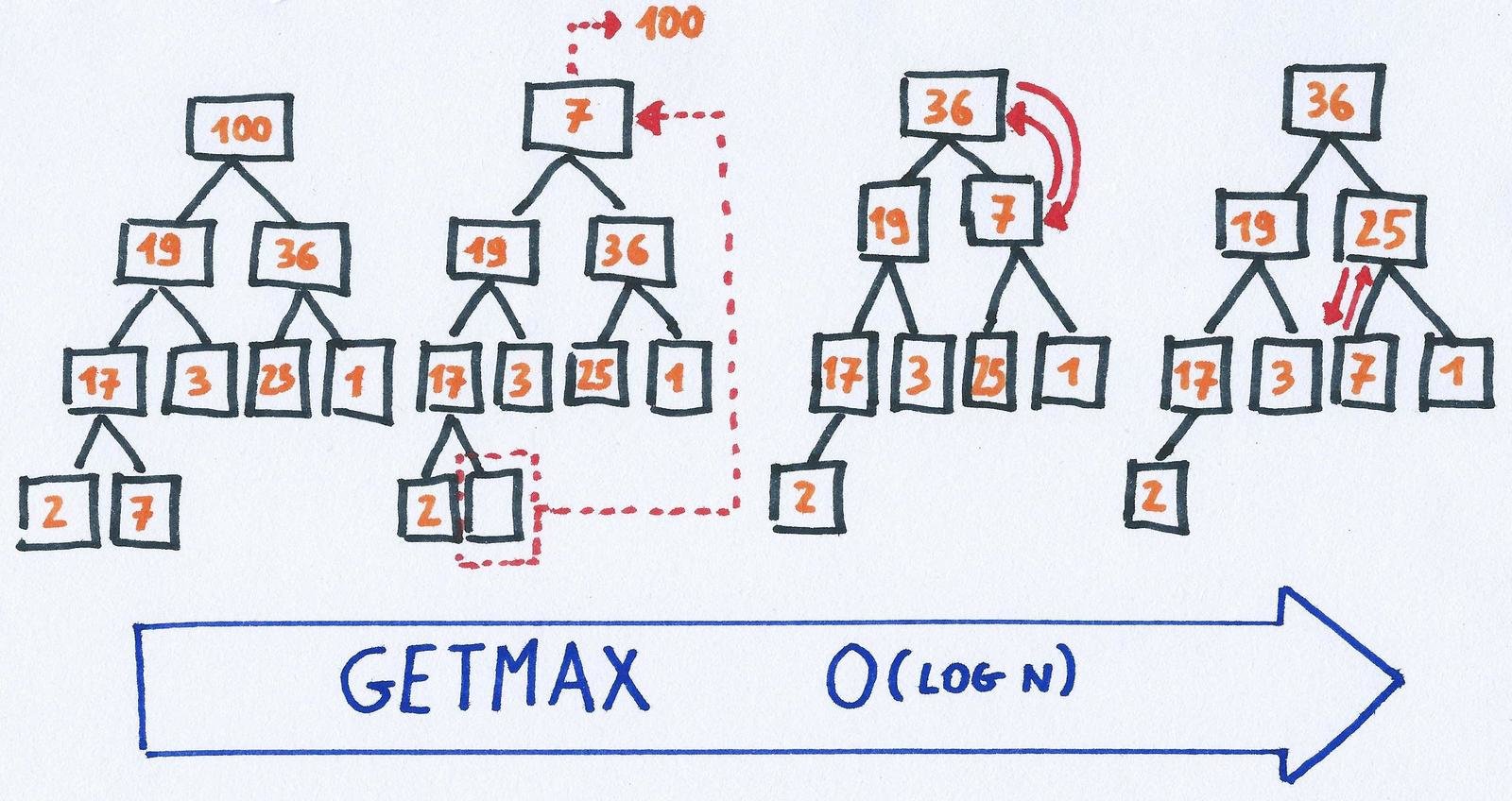
Heap
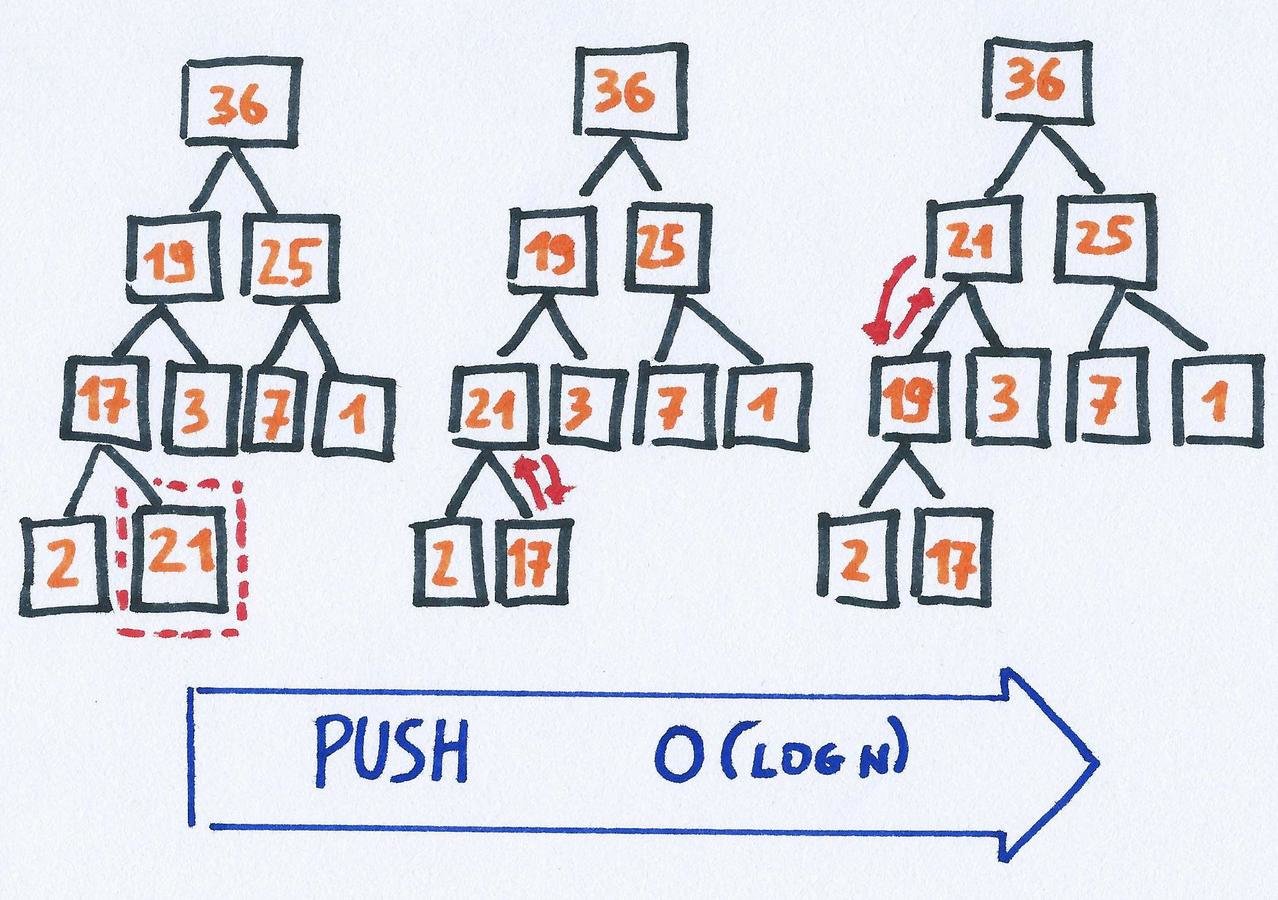
Other applications
Heapsort O(n log n)
Shortest path algorithm
Order statistic (kth smallest/largest item)
Roll your own or get it from npm:
Stack
Queue
Double ended queue
Circular array
Tree
Graph
...
Use the right tool for the job