Designer uncertainty and agent uncertainty
Martin Biehl (Cross Labs)
Nathaniel Virgo (Earth-Life Science Institute)




Made possible via funding by:
Overview
- Designing artificial agents using probabilistic inference
- Designer uncertainty / problem uncertainty
- Agent uncertainty
- Recap
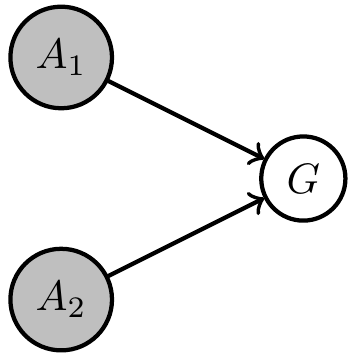
Designing artificial agents
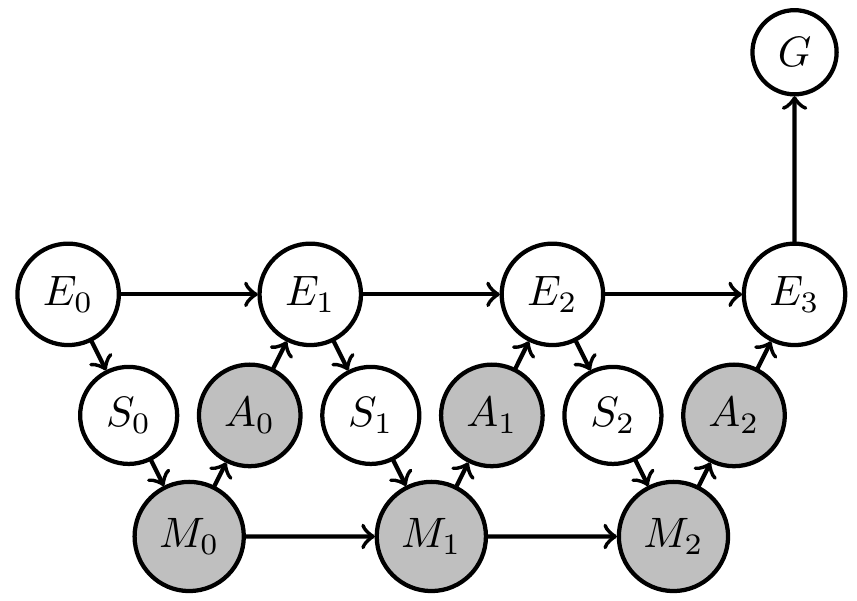
When we design artificial agents we usually know something about
- dynamics of environment \(E\) the agent will face
- sensor values \(S\) available to it
- actions \(A\) it can take
- goal \(G\) it should achieve
Then want to find
- dynamics of memory \(M\)
- selection of actions \(A\)
- that achieve the goal (or make it likely)
We show how
- express problem of designers of artificial agents face
- designers can incorporate their own uncertainty into the problem and leave it to the artificial agent to resolve it
- to ensure that the artificial agent has a Bayesian interpretation and therefore it's own well defined uncertainty
Perspective: design as planning
Designing artificial agents
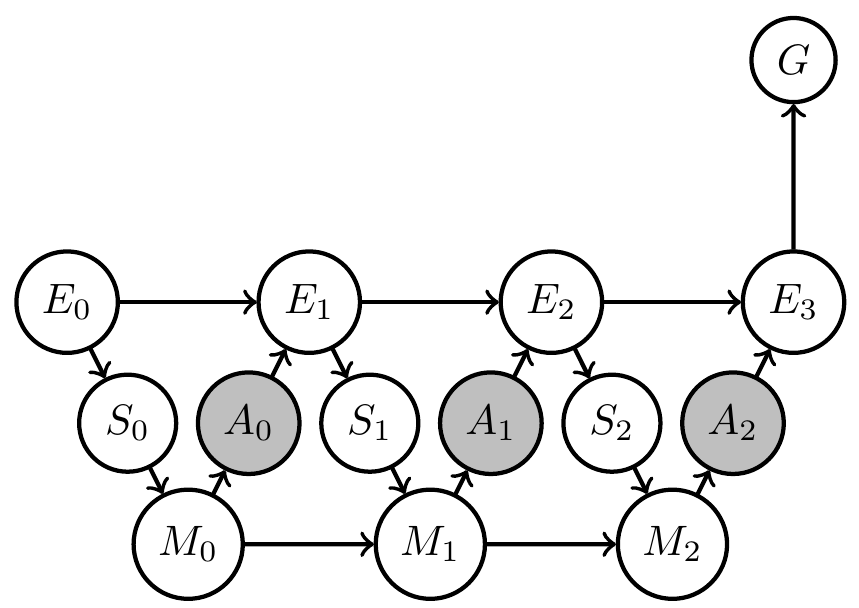
Formally represent what we know and what we don't know via Bayesian network with
- known Markov kernels (white)
- unknown Markov kernels (grey)
- goal-achieved-variable \(G\)

Designing artificial agents
- Bayesian network:
- Set of random variables \(X=(X_1,..,X_n)\)
- each variable \(X_i\) has associated
- node \(i \in V\) in a directed acyclic graph
- Markov kernel \(p(x_i|x_{\text{pa}(i)})\) defining its dependence on other variables
- Joint probability distribution factorizes according to the graph:
\[\newcommand{\pa}{\text{pa}}p(x) = \prod_{v\in V} p(x_v | x_{\pa(v)}).\]

Designing artificial agents
- Bayesian network:
- We distinguish:
- known kernels \(B\subset V\)
- unknown kernels \(U\subset V\)
- then:
\[\newcommand{\pa}{\text{pa}}p(x) = \prod_{u\in U} p_u(x_a | x_{\pa(a)}) \, \prod_{b\in B} \bar p_b(x_b | x_{\pa(b)})\]
- We distinguish:

Designing artificial agents
Find unknown kernels \(p_U:=\{p_u: u \in U\}\)
- maximize probability of achieving the goal:
\[p_U^* = \text{arg} \max_{p_U} p(G=1).\]
a.k.a. planning as inference [*] - equivalent to maximum likelihood inference
- automates design of agent memory dynamics and action selection (but hard to solve)

[*] Matthew Botvinick and Marc Toussaint. Planning as inference. Trends in cognitive sciences, 16(10):485–488, 2012.
Example: 2-armed bandit
- Constant hidden "environment state" \(\phi=(\phi_1,\phi_2)\) storing win probabilities of two arms
- agent action is choice of arm \(a_t \in \{1,2\}\)
- sensor value is either win or lose sampled according to win probability of chosen arm \(s_t \in \{\text{win},\text{lose}\}\)
\[p_{S_t}(s_t|a_{t-1},\phi)=\phi_{a_{t-1}}^{\delta_{\text{win}}(s_t)} (1-\phi_{a_{t-1}})^{\delta_{\text{lose}}(s_t)}\] - goal is achieved if last arm choice results in win \(s_3=\text{win}\)
\[p_G(G=1|s_3)=\delta_{\text{win}}(s_3)\] - memory \(m_t \in \{1,2,3,4\}\) is enough to store all different results.
Example: 2-armed bandit
- Environment contains two arms with fixed win probabilities
\[p_U^* = \text{arg} \max_{p_U} p(G=1).\]
a.k.a. planning as inference [*]
- equivalent to maximum likelihood inference
- automates design of agent memory dynamics and action selection (but hard to solve)
[*] Matthew Botvinick and Marc Toussaint. Planning as inference. Trends in cognitive sciences, 16(10):485–488, 2012.
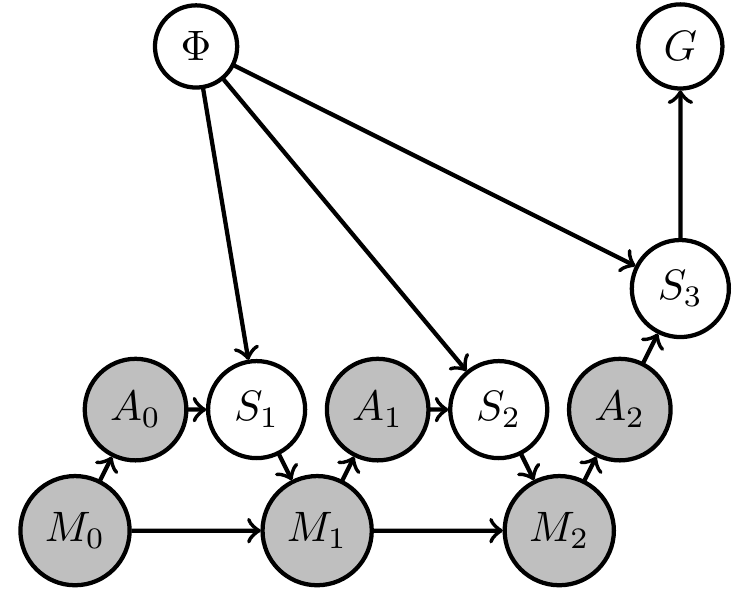
Two situations:
- designer uncertain about environment dynamics
- agent supposed to deal with different environments
Explicitly reflect this by
- additional variable \(\phi\)
- prior distribution over \(\phi\)
Designer uncertainty

Then
- agent will find out what is necessary to achieve goal
- i.e. it will trade off exploration (try out different arms) and exploitation (winning)
- comparable to meta-learning
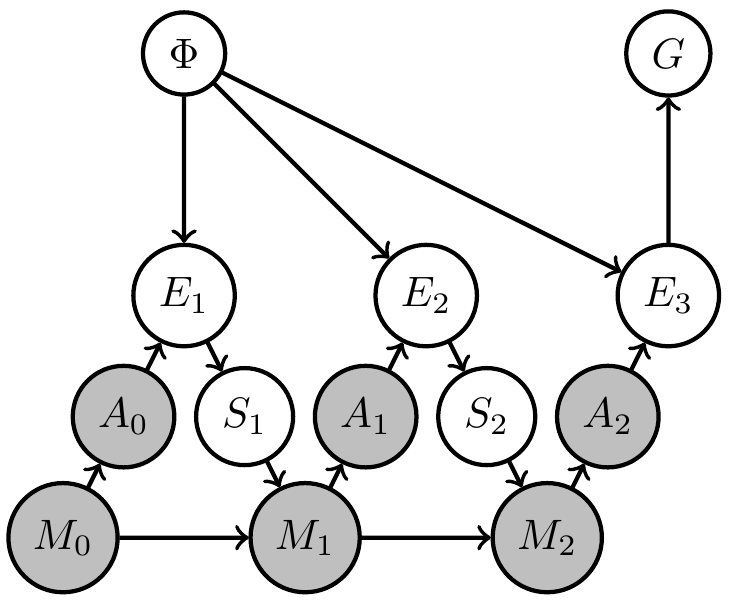
Designer uncertainty


Can also make another kind of uncertainty explicit
- choose model that agent should have of causes of its sensor values
- fix memory dynamics \(p_M(m_t|s_t,m_{t-1})\) such that it has consistent Bayesian interpretation w.r.t chosen model
- only action kernels \(p_A(a_t|m_t)\) unknown
Agent uncertainty

Then by construction
- know a consistent Bayesian interpretation
- i.e.\ an interpretation map \(\psi:M \to PH\)
- well defined agent uncertainty in state \(m_t\) via Shannon entropy \[H_{\text{Shannon}}(m_t):=\sum_{h} \psi(h||m_t) \log \psi(h||m_t)\]
- information gain from \(m_0\) to \(m_t\) by KL divergence \[D_{\text{KL}}[m_t||m_0]:=\sum_h \psi(h||m_t) \log \frac{\psi(h||m_t)}{\psi(h||m_0)}\]
Agent uncertainty
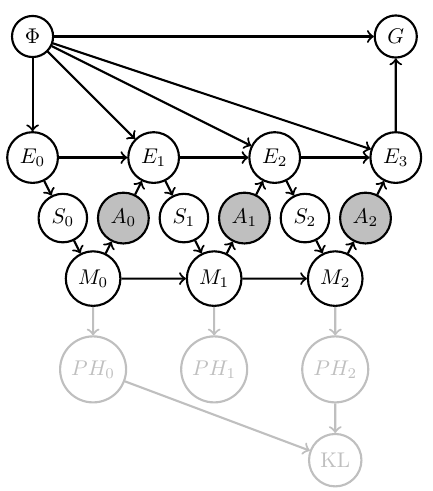
Note:
- can then also turn this information gain into a goal to create intrinsically motivated agent
- (some trick is needed...)
Agent uncertainty

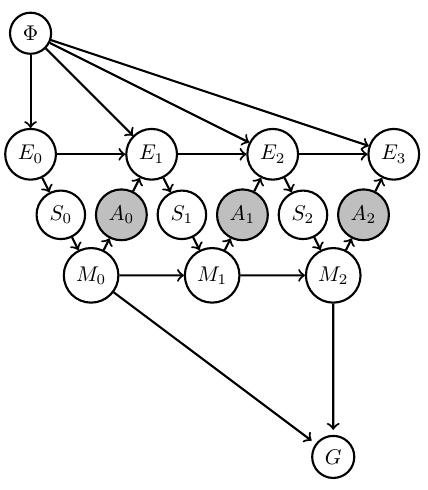
- Considered design of artificial agents as planning task
- formalized planning task as inference problem in Bayesian network
- can explicitly reflect designer's uncertainty / knowledge
- resulting agents automatically trade of exploration and exploitation
- constructing interpretable agent memory allows calculation of (subjective) agent uncertainty and information gain
Recap


Perspective: "design as inference"
Underlying perspective:
- view design of artificial agents as planning task:
- usually planning means find (own) actions that achieve a goal
- when designing an artificial agent also create a kind of "plan" but
- it will be executed by something else (e.g. computer)
- must explicitly plan "internal actions" like what to remember (memory update)
Perspective: "design as inference"
Underlying perspective:
- design of artificial agents similar to planning task:
- usually planning means find (own) actions that achieve a goal
- when designing an artificial agent to achieve a goal:
- also create a kind of "plan" but
- plan will be executed by something else (e.g. computer)
- plan must include "internal actions" like plan of what to remember (memory update)
Underlying perspective:
- known: planning can be done by probabilistic inference
\(\Rightarrow\) if we formulate agent design problems as planning problems they become inference problems
Perspective: "design as inference"
Perspective: design as planning
Underlying perspective:
- view design of artificial agents as planning task:
- use formal way to represent this planning task (planning as inference)
- gives us formal way to design agents
design as planning \(\to\) planning as inference
\(\Rightarrow\) design as inference?
General setting
Assume
- want to achieve some goal
- know:
- the environment you want to achieve it in
- actions you can take
- observations you will be able to make
Then
- planning is the process of finding actions that lead to goal
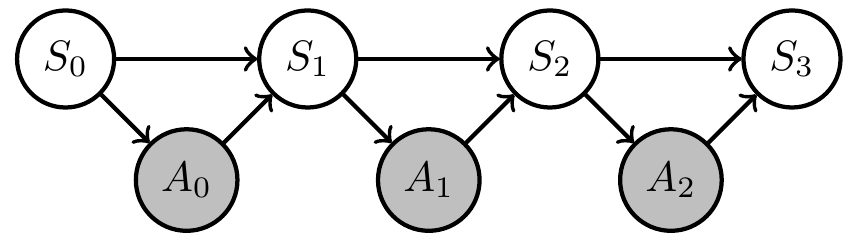
POMDPs
Formalize as POMDP:
- Known:
- goal
- environment/world state \(W\) with dynamics: \(p(w_{t+1}|w_t,a_t)\)
- observations / sensor values \(S\): \(p(s_t|w_t)\)
Planning as inference
Terminology:
- Planning:
- finding policy parameters that maximize probability of achieving a goal
- Maximum likelihood inference:
- finding model parameters that maximize probability of data
Planning as inference
What is it good for?
Automatically find a probabilistic policy to achieve a goal.
What do you need to use it?
- probabilistically specified problem!
- dynamics of environment (including influence of actions)
- inputs / sensor values / observation available to policy
- goal
Planning as inference
Combination:
- Planning as inference (PAI):
- Consider the achievement of the goal as the only available data
- ensure policy parameters are the only model parameters
- then maximizing likelihood of data maximizes likelihood of achieving the goal
\(\Rightarrow\) can use max. likelihood to solve planning!
Maximum likelihood inference
Given:
- Statistical model:
- set \(X\) of possible observations
- parameterized set \(\{p_\phi:\phi \in \Phi\}\) of probability distributions \(p_\phi(x)\) over \(X\)
- Observation \(\bar x \in X\)
Find parameter \(\phi^*\) that maximizes likelihood of the observations:
\[\phi^*=\text{arg} \max_\phi p_\phi(\bar x)\]
Maximum likelihood inference
Example: Maximum likelihood inference of coin bias
- Statistical model:
- \(X=\{(x_1,...,x_n): x_i \in \{\text{heads},\text{tails}\}\}\)
- \(\{p_\phi(x)= \phi^{c_{\text{heads}}(x)} (1-\phi)^{c_{\text{tails}}(x)}:\phi \in [0,1]\}\)
- Observation \(\bar x \in X\)
Then:
\[\phi^*=\text{arg} \max_\phi p_\phi(\bar x)=\frac{c_{\text{heads}}(\bar x)}{c_{\text{heads}}(\bar x)+c_{\text{tails}}(\bar x)}\]
Maximum likelihood inference
Example: Maximum likelihood inference of coin bias
- Statistical model:
- observations are sequences of outcomes \(X=\{(x_1,...,x_n): x_i \in \{\text{heads},\text{tails}\}\}\)
- parameterized set of distributions \(\{p_\phi:\phi \in [0,1]\}\) with
\[p_\phi(x)= \phi^{c_{\text{heads}}(x)} (1-\phi)^{c_{\text{tails}}(x)}\]
here \(c_{\text{heads}}(x)\) , \(c_{\text{tails}}(x)\) count occurrences of heads/tails in \(x\)
- Observation \(\bar x \in X\)
Find parameter \(\phi^*\) that maximizes likelihood of the observations:
\[\phi^*=\text{arg} \max_\phi p_\phi(\bar x)\]
Maximum likelihood inference
Example: Maximum likelihood inference of coin bias
- Statistical model:
- observations are sequences of outcomes \(X=\{(x_1,...,x_n): x_i \in \{\text{heads},\text{tails}\}\}\)
- parameterized set \(\{p_\phi:\phi \in \Phi=\[0,1\]\}\) with
\[p_\phi(x)= \prod_{i=1}^n \phi^{\delta_{\text{heads}}(x_i)} (1-\phi)^{\delta_{\text{tails}}(x_i)}\]
- Observation \(\bar x \in X\)
Find parameter \(\phi^*\) that maximizes likelihood of the observations:
\[\phi^*=\text{arg} \max_\phi p_\phi(\bar x)\]
Maximum likelihood inference
Example: Maximum likelihood inference of coin bias
- Statistical model:
- observations are sequences of outcomes \(X=\{(x_1,...,x_n): x_i \in \{\text{heads},\text{tails}\}\}\)
- parameterized set \(\{p_\phi:\phi \in \Phi=\[0,1\]\}\) with
\[p_\phi(x)= \prod_{i=1}^n \phi^{\delta_{\text{heads}}(x_i)} (1-\phi)^{\delta_{\text{tails}}(x_i)}\]
- Observation \(\bar x \in X\)
Find parameter \(\phi^*\) that maximizes likelihood of the observations:
\[\phi^*=\text{arg} \max_\phi p_\phi(\bar x)\]
Planning as inference
Note that for maximum lik
- Set of observations can be arbitrarily simple
- Set of probability distributions can be arbitrarily complicated
So we can use :
- Binary "goal-achieved-variable" with \(G=\{g,\neg g\}\) for observations
- Bayesian networks (with hidden variables) for specifying the sets of probability distributions
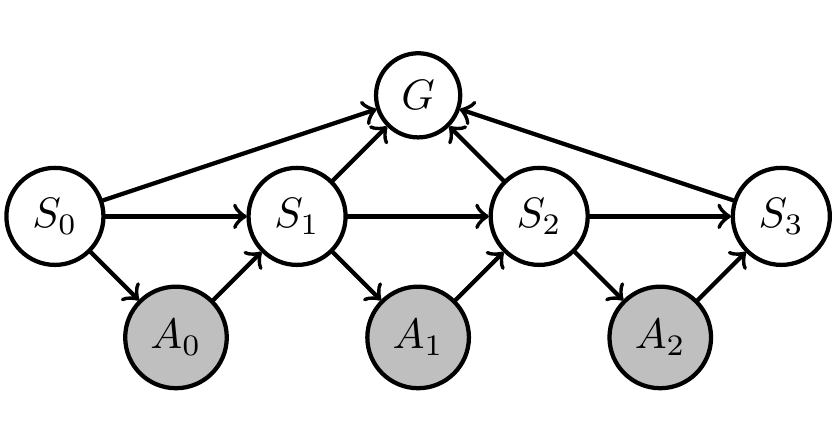
Planning as inference
- Problem structures as Bayesian networks:
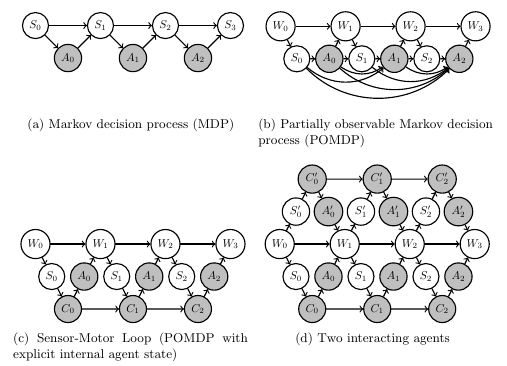
Planning as inference
Bayesian network
goal
- Represent goals and policies by sets of probability distributions:
-
goal must be an event i.e. function \(G(x)\) with
- \(G(x)=1\) if goal is achieved
- \(G(x)=0\) else.
-
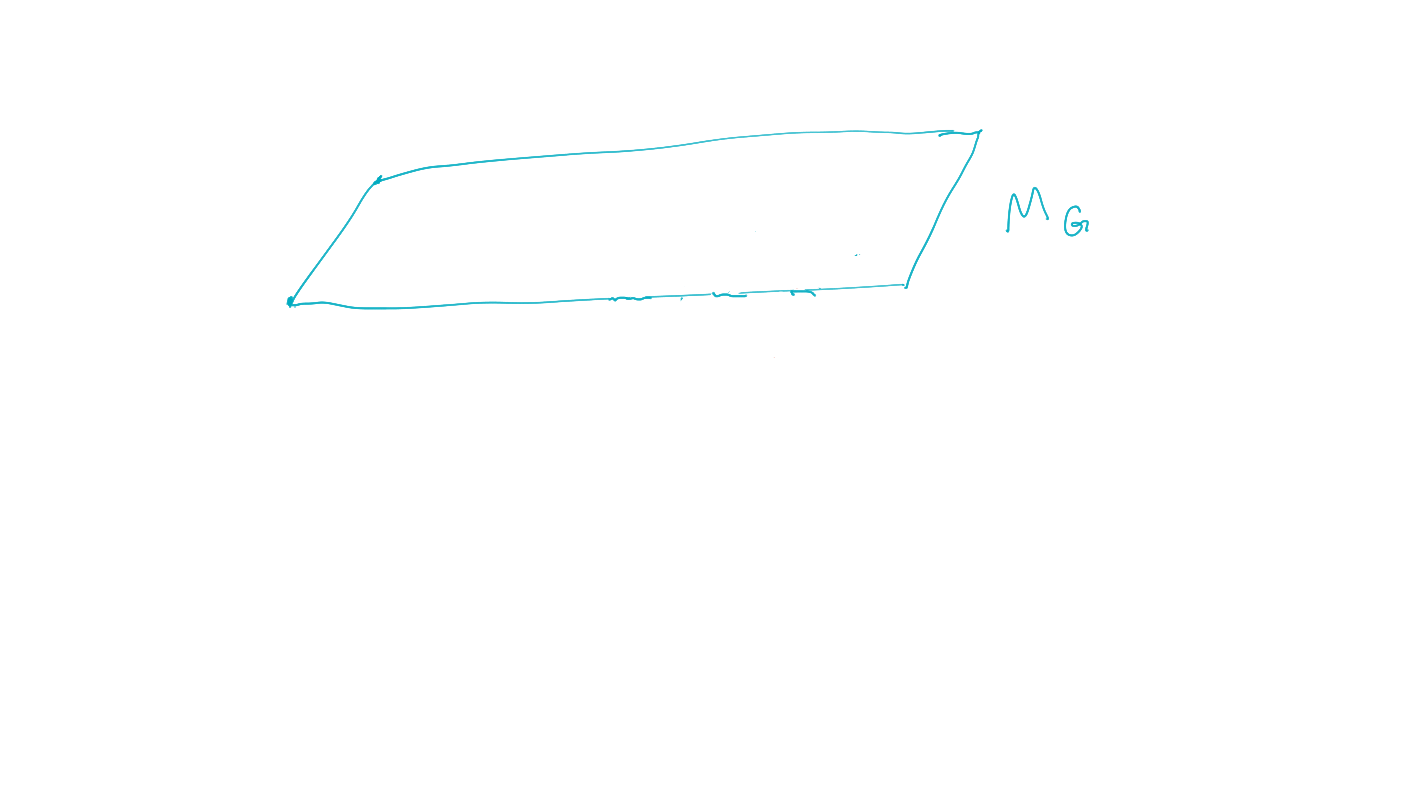
goal manifold is set of distributions where the goal event occurs with probability one:
\[M_G:=\{P: p(G=1)=1\}\]
-
goal must be an event i.e. function \(G(x)\) with
Planning as inference
- Find policies that maximize probability of goal via geometric EM algorithm:
-
planning as inference finds policy / agent kernels such that:
\[P^* = \text{arg} \max_{P \in M_A} p(G=1).\] - (compare to maximum likelihood inference)
-
planning as inference finds policy / agent kernels such that:

Bayesian network
goal
policies
Planning as inference
Practical side of original framework:
- Represent
- Planning problem structure by Bayesian networks
- Goal and possible policies by sets of probability distributions
- Find policies that maximize probability of goal via geometric EM algorithm.

Bayesian network
goal
policies
Expected reward maximization
- PAI finds policy that maximizes probability of the goal event:
\[P^* = \text{arg} \max_{P \in M_A} p(G=1).\] - Often want to maximize expected reward of a policy:
\[P^* = \text{arg} \max_{P \in M_A} \mathbb{E}_P[r]\] - Can we solve the second problem via the first?
- Yes, at least if reward has a finite range \([r_{\text{min}},r_{\text{max}}]\):
- add binary goal node \(G\) to Bayesian network and set:
\[\newcommand{\ma}{{\text{max}}}\newcommand{\mi}{{\text{min}}}\newcommand{\bs}{\backslash}p(G=1|x):= \frac{r(x)-r_\mi}{r_\ma-r_\mi}.\]
- add binary goal node \(G\) to Bayesian network and set:

Expected reward maximization
- Example application: Markov decision process
- reward only depending on states \(S_0,...,S_3\): \[r(x):=r(s_0,s_1,s_2,s_3)\]
- reward is sum over reward at each step:
\[r(s_0,s_1,s_2,s_3):= \sum_i r_i(s_i)\]
Planning as inference
- Represent goals and policies by sets of probability distributions:
-
policy is a choice of the changeable Markov kernels
\[\newcommand{\pa}{\text{pa}}\{p(x_a | x_{\pa(a)}):a \in A\}\] -
agent manifold/policy manifold is set of distributions that can be achieved by varying policy
\[\newcommand{\pa}{\text{pa}}p(x) = \prod_{a\in A} p(x_a | x_{\pa(a)}) \, \prod_{b\in B} \bar p(x_b | x_{\pa(b)})\]
-
policy is a choice of the changeable Markov kernels

Bayesian network
goal

policies
Planning as inference
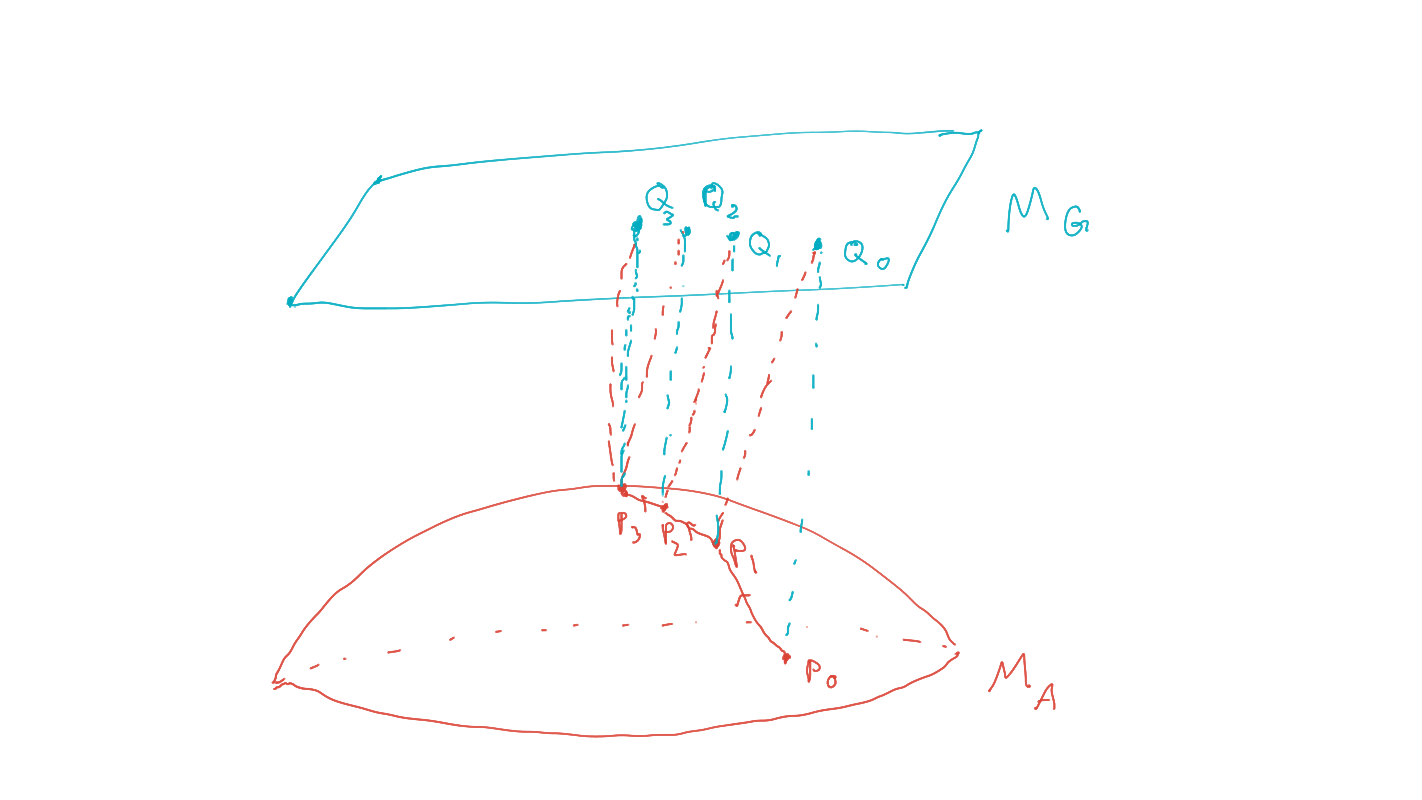
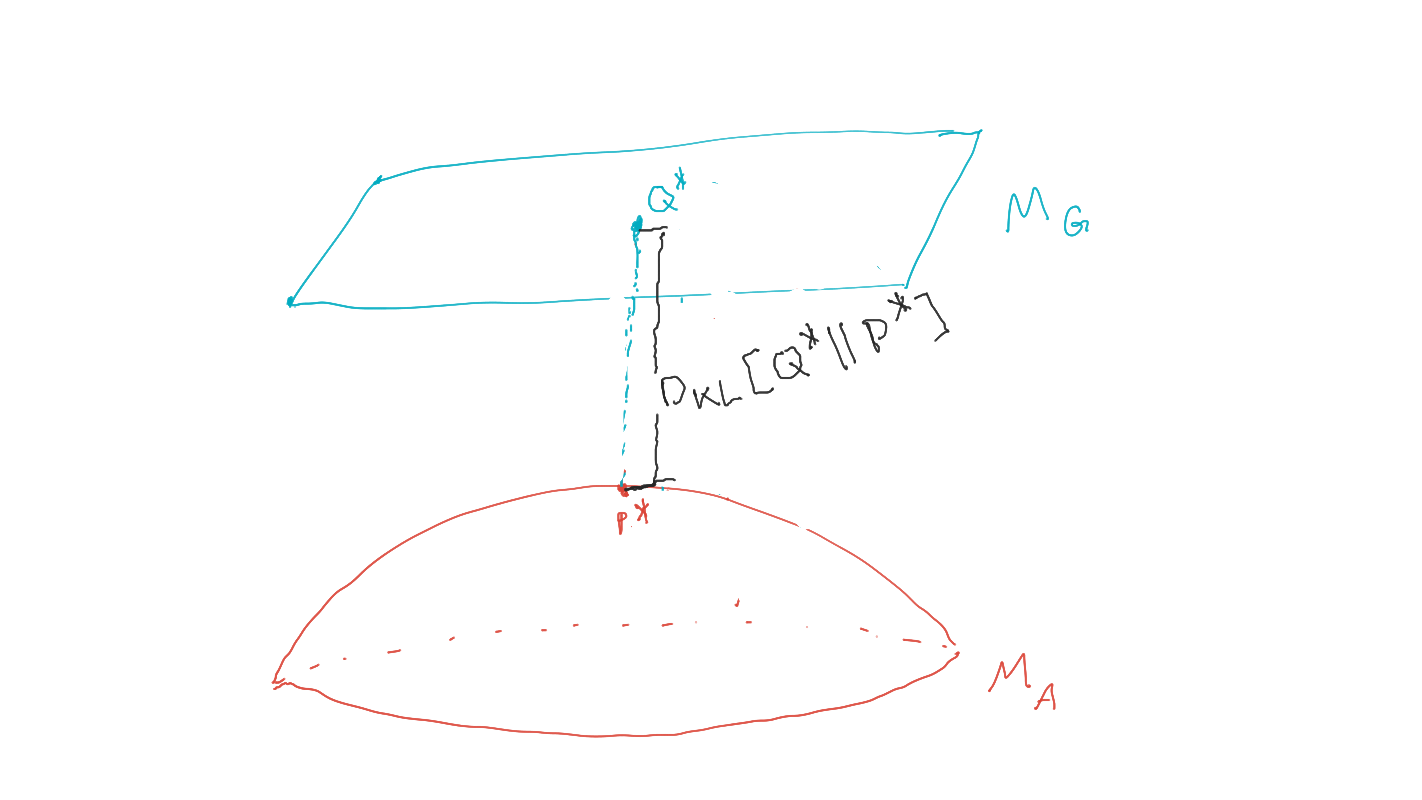
- Find policies that maximize probability of goal via geometric EM algorithm:
- Can prove that \(P^*\) is the distribution in agent manifold closest to goal manifold in terms of KL-divergence
- Local minimizers of this KL-divergence can be found with the geometric EM algorithm

Bayesian network
goal
policies
Planning as inference
- Find policies that maximize probability of goal via geometric EM algorithm:
- Start with an initial prior, \(P_0 \in M_A\) .
- (e-projection)
\[Q_t = \text{arg} \min_{Q\in M_G} D_{KL}(Q∥P_t )\] - (m-projection)
\[P_{t+1} = \text{arg} \min_{P \in M_A} D_{KL} (Q_t ∥P )\]


Bayesian network
goal
policies
Planning as inference
- Find policies that maximize probability of goal via geometric EM algorithm:
- Equivalent algorithm using only marginalization and conditioning:
- Initial agent kernels define prior, \(P_0 \in M_A\).
- Get \(Q_t\), from \(P_t\) by conditioning on the goal: \[q_t(x) = p_t(x|G=1).\]
- Get \(P_{t+1}\), by replacing agent kernels by conditional distributions in \(Q_t\):
\[\newcommand{\pa}{\text{pa}} p_{t+1}(x) = \prod_{a\in A} q_t(x_a | x_{\pa(a)}) \, \prod_{b\in B} \bar p(x_b | x_{\pa(b)})\]
\[\newcommand{\pa}{\text{pa}} \;\;\;\;\;\;\;= \prod_{a\in A} p_t(x_a | x_{\pa(a)},g) \, \prod_{b\in B} \bar p(x_b | x_{\pa(b)})\]
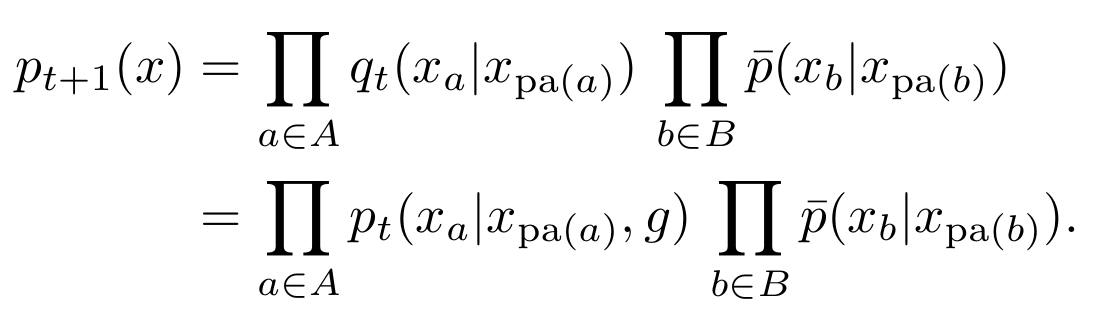
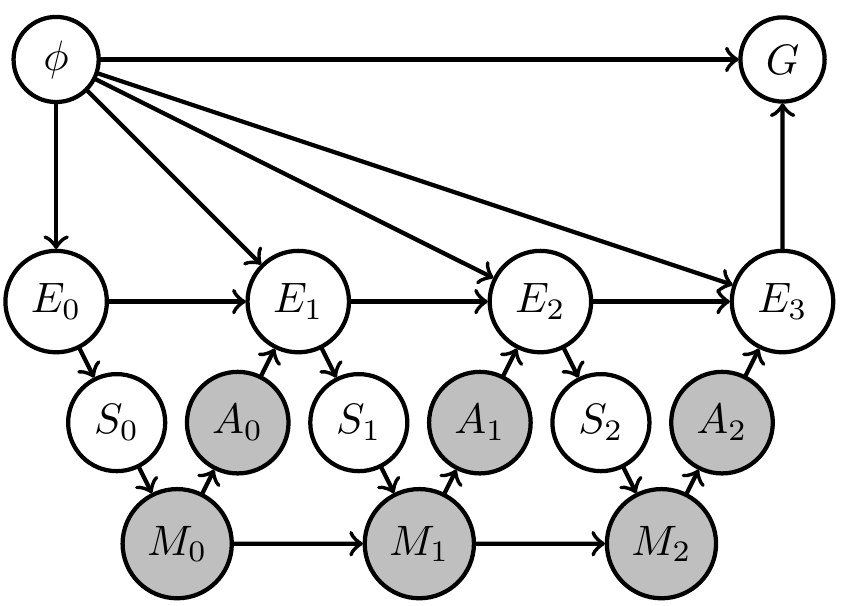
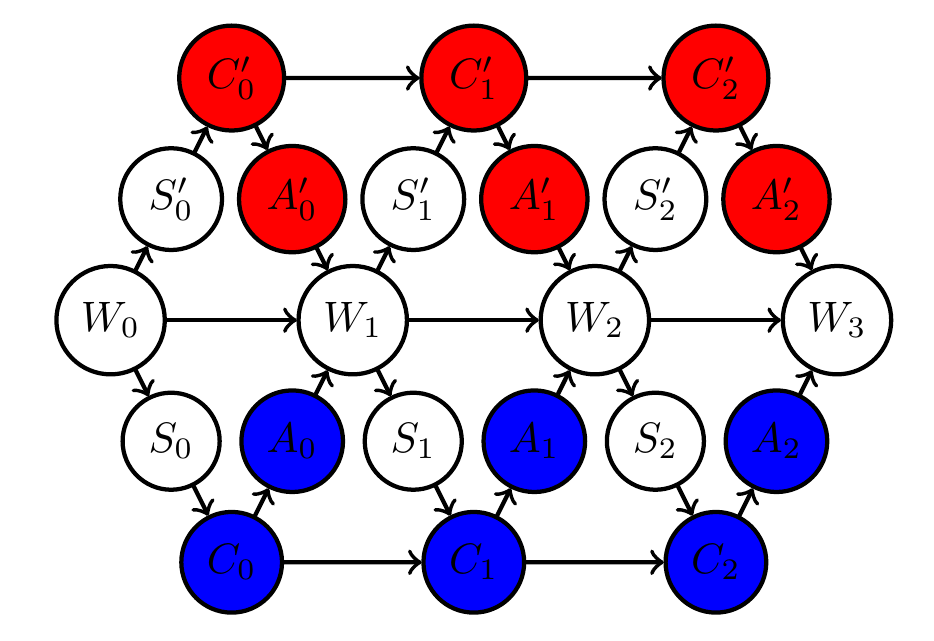
Uncertain (PO)MDP
- Assume
- (as usual) transition kernel of environment is constant over time, but
- we are uncertain about what is the transition kernel
- How can we reflect this in our setup / PAI?
- Can we find agent kernels that solve problem in a way that is robust against variation of those transition kernels?
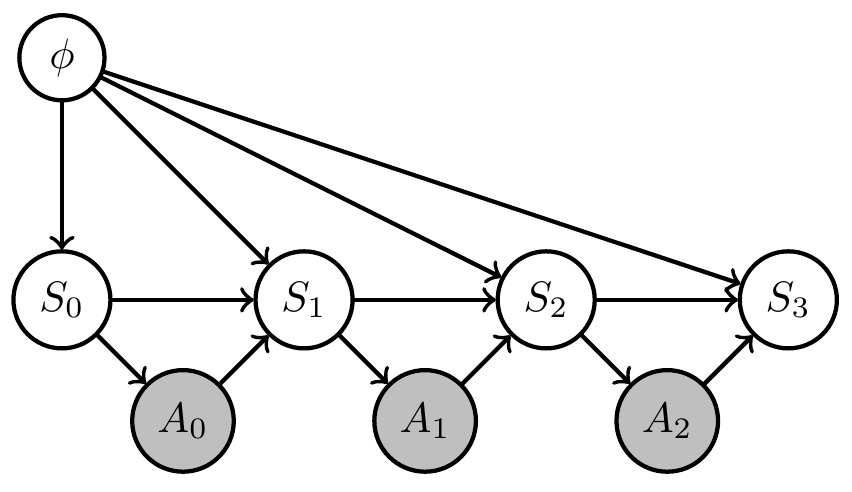
Uncertain (PO)MDP
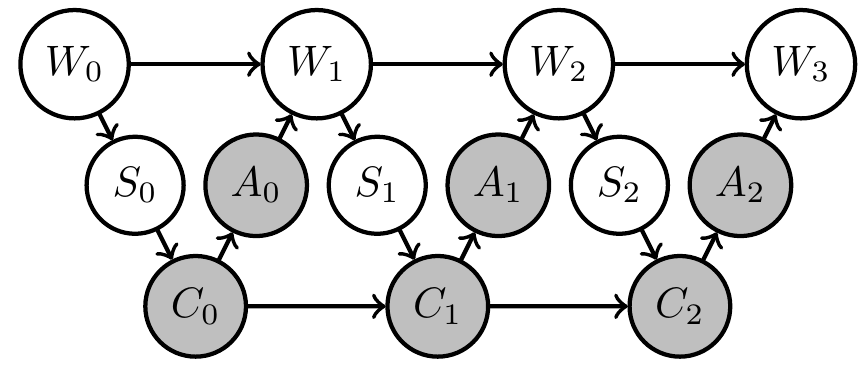
- Extend original (PO)MDP Bayesian network with two steps:
- parametrize environment transition kernels by shared parameter \(\phi\):
\[\bar{p}(x_e|x_{\text{pa}(e)}) \to \bar{p}_\phi(x_e|x_{\text{pa}(e)},\phi)\] - introduce prior distribution \(\bar{p}(\phi)\) over environment parameter
- parametrize environment transition kernels by shared parameter \(\phi\):
Uncertain (PO)MDP


- Same structure can be hidden in original network but in this way becomes a requirement/constraint
- If increasing goal probability involves actions that resolve uncertainty about the environment then PAI finds those actions!
- PAI results in curious agent kernels/policy.
Uncertain (PO)MDP
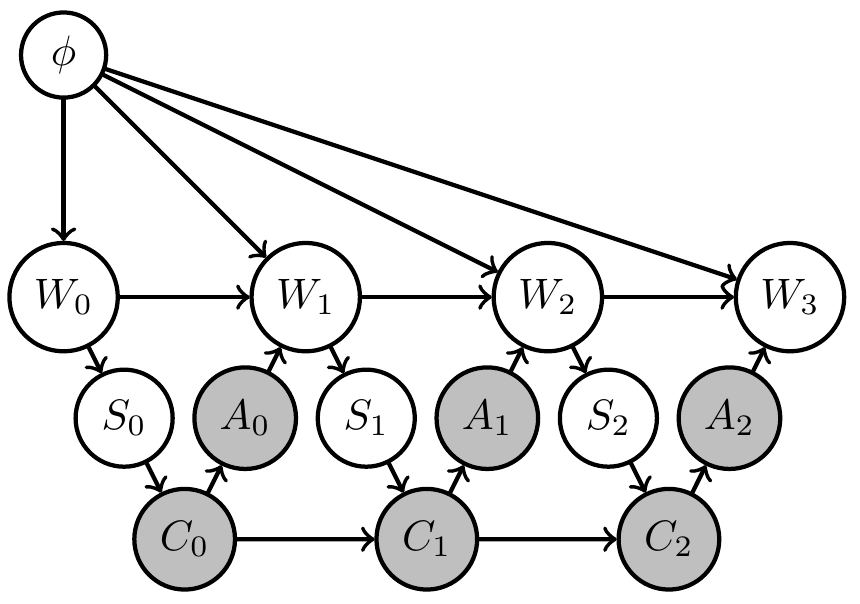
- Same structure can be hidden in original network but in this way becomes a requirement/constraint
- If increasing goal probability involves actions that resolve uncertainty about the environment then PAI finds those actions!
- PAI results in curious agent kernels/policy.
Uncertain (PO)MDP
-
Relevance for project:
- agents that can achieve goals in unknown / uncertain environments are important for AGI
- related to meta-learning
- understanding knowledge and uncertainty representation is important for agent design in general
Related project funded
- John Templeton Foundation has funded related project titled: Bayesian agents in a physical world
- Goal:
- What does it mean that a physical system (dynamical system) contains a (Bayesian) agent?
Related project funded
- Starting point:
- given system with inputs defined by
\[f:C \times S \to C\] - define a consistent Bayesian interpretation as:
- model / Markov kernel \(q: H \to PS\)
- interpretation function \(g:C \to PH\)
such that
\[g(c_{t+1})(h)=g(f(c_t,s_t))(h)=\frac{q(s_t|h) g(c_t)(h)}{\sum_{\bar h} q(s_t|\bar h) g(c_t)(\bar h)} \]
- given system with inputs defined by
Related project funded
- more suggestive notation:
\[g(h|c_{t+1})=g(h|f(c_t,s_t))=\frac{q(s_t|h) g(h|c_t)}{\sum_{\bar h} q(s_t|\bar h) g(\bar h|c_t)} \] - but note: \(PH_i\) are deterministic random variables and need no extra sample space
- \(H\) isn't even a deterministic random variable (what???)
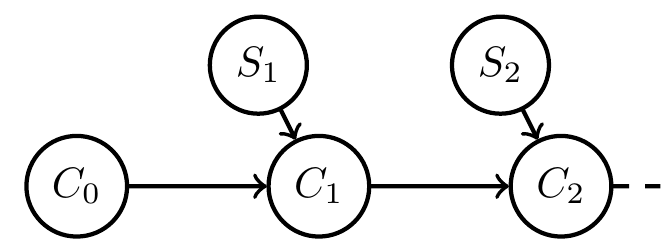
Related project funded
- Take away message :
- Formal condition for when a dynamical system with inputs can be interpreted as consistently updating probabilistic beliefs about the causes of its inputs (e.g. environment)
- Extensions to include stochastic systems, actions, goals, etc. ongoing...


Related project funded
- Relevance for project
- deeper understanding of relation between physical systems and agents will also help in thinking about more applied aspects
- a lot of physical agents are made of smaller agents and grow / change their composition, understanding this is also part of the funded project and is also directly relevant for the point "dynamical scalability of multi-agent systems" in the proposal
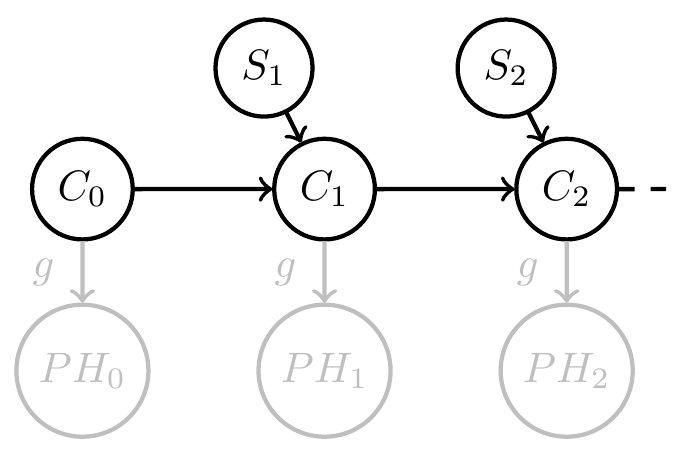
Two kinds of uncertainty
- Designer uncertainty:
- model our own uncertainty about environment when designing the agent to make it more robust / general
- Agent uncertainty:
- constructing an agent that uses specific probabilistic belief update method
- exact Bayesian belief updating (exponential families and conjugate priors)
- approximate belief updating (VAE world models?)
- constructing an agent that uses specific probabilistic belief update method
Two kinds of uncertainty
- Designer uncertainty:
- introduce hidden parameter \(\phi\) with prior \(\bar p(\phi)\) among fixed kernels
- planning as inference finds agent kernels / policy that deal with this uncertainty

Two kinds of uncertainty
- Agent uncertainty:
- In perception-action loop:
- construct agent's memory transition kernels that consistently update probabilistic beliefs about their environment
- these beliefs come with uncertainty
- can turn uncertainty reduction itself into a goal!
- In perception-action loop:
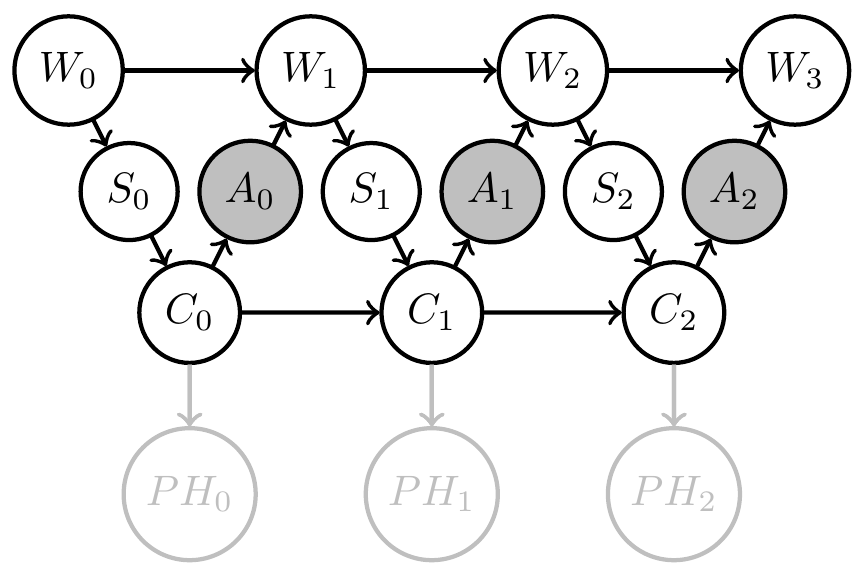
Two kinds of uncertainty

- Agent uncertainty:
- E.g: Define goal event via information gain :
\[G=1 \Leftrightarrow D_{KL}[PH_2(x)||PH_0(x)] > d\] - PAI solves for policy that employs agent memory to gain information / reduce its uncertainty by \(d\) bits
- E.g: Define goal event via information gain :
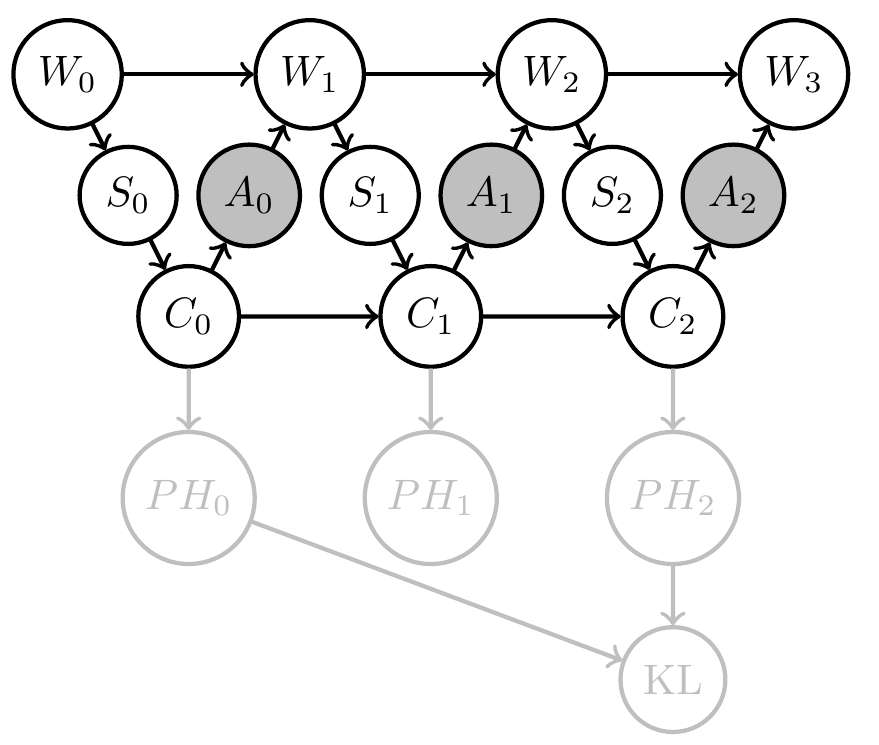
Two kinds of uncertainty
-
Relevance for project:
- taking decisions based on agent's knowledge is part of the project
Progress
- Successfully extended framework by features necessary for tackling goals of our project.
- These are discussed next:
- Expected reward maximization
- Parametrized kernels
- Shared kernels
- Multi-agent setup and games
- Uncertain (PO)MDP
- Related project funded
- Two uncertainties: designer and agent uncertainty
- Relevance for project will be highlighted
Expected reward maximization
- Relevance for project:
- reward based problems more common than goal event problems ((PO)MDPs, RL, losses...)
- extends applicability of framework
Parametrized kernels
- Often we don't want to choose the agent kernels completely freely e.g.:
- choose parametrized agent kernels
\[p(x_a|x_{\text{pa}(a)}) \to p(x_a|x_{\text{pa}(a)},\theta_a)\]
- choose parametrized agent kernels
- What do we have to adapt in this case?
- Step 3 of EM algorithm has to be adapted
Parametrized kernels
- Algorithm for parametrized kernels (not only conditioning and marginalizing anymore):
- Initial parameters \(\theta(0)\) define prior, \(P_0 \in M_A\).
- Get \(Q_t\), from \(P_t\) by conditioning on the goal: \[q_t(x) = p_t(x|G=1).\]
- Get \(P_{t+1}\), by replacing parameter \(\theta_a\) of each agent kernel with result of:
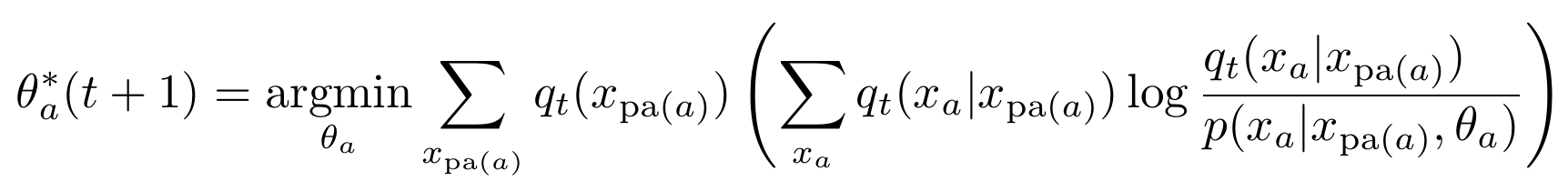
Parametrized kernels
- Relevance for project:
- needed for shared kernels
- needed for continuous random variables
- neural networks are parametrized kernels
- scalability
Shared kernels
- We also often want to impose the condition that multiple agent kernels are identical
- E.g. the three agent kernels in this MDP:

Shared kernels
- Introduce "types" for agent kernels
- let \(c(a)\) be the type of kernel \(a \in A\)
- kernels of same type share
- input spaces
- output space
- parameter
- then \(p_{c(a)}(x_a|x_{\text{pa}(a)},\theta_c)\) is the kernel of all nodes with \(c(a)=c\).
Shared kernels
- Example agent manifold change under shared kernels
Shared kernels
- Algorithm then becomes
- Initial parameters \(\theta(0)\) define prior, \(P_0 \in M_A\).
- Get \(Q_t\), from \(P_t\) by conditioning on the goal: \[q_t(x) = p_t(x|G=1).\]
- Get \(P_{t+1}\), by replacing parameter \(\theta_c\) of all agent kernels of type \(c\) with result of:
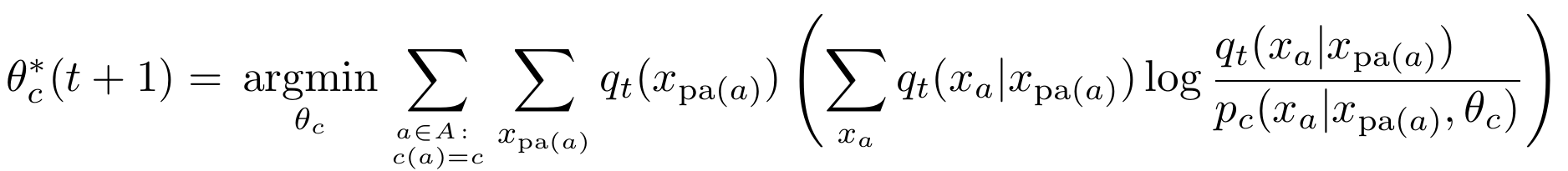
Proposal
- Exploit planning as inference setup to answer questions about:
-
Multiple, possibly competing goals
-
Coordination and communication from an information theoretic perspective
-
Dynamic scalability of multi-agent systems
-
Dynamically changing goals that depend on knowledge acquired through observations
-
Shared kernels
- Relevance for project:
- scalability (less parameters to optimize)
- make it possible to have
- multiple agents with same policy
- constant policy over time
Multi-agent setup
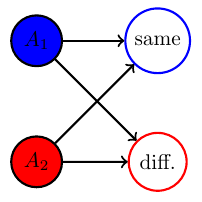
Example multi agent setups:
Two agents interacting with same environment
Two agents with same goal
Two agents with different goals
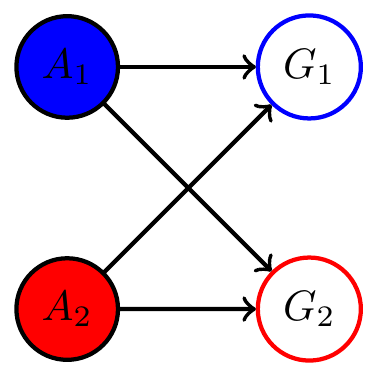
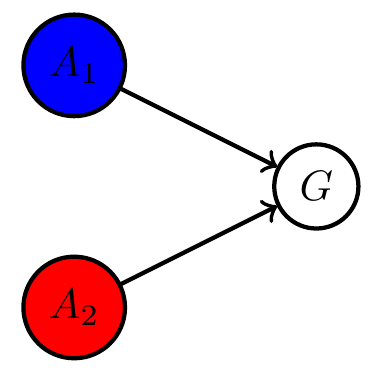
Multi-agent setup
- Note:
- In cooperative setting:
- can often combine multiple goals to single common goal via event intersection, union, complement (supplied by \(\sigma\)-algebra)
- single goal manifold
- in principle can use single agent PAI as before
- In cooperative setting:


Multi-agent setup
- Note:
- In non-cooperative setting:
- goal events have empty intersection
- no common goal
- multiple disjoint goal manifolds
- goal events have empty intersection
- In non-cooperative setting:

Multi-agent setup
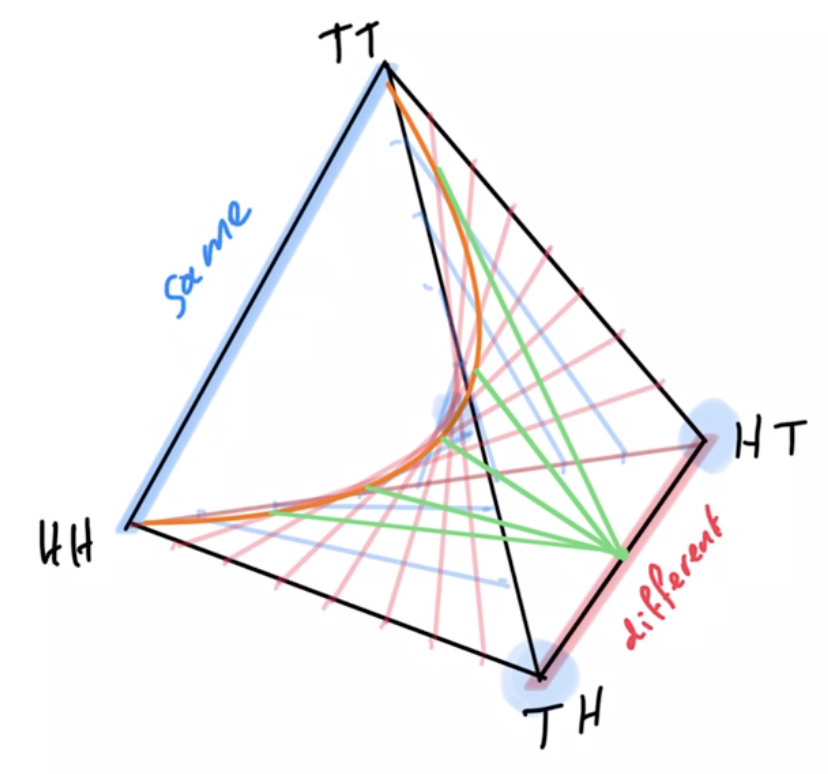
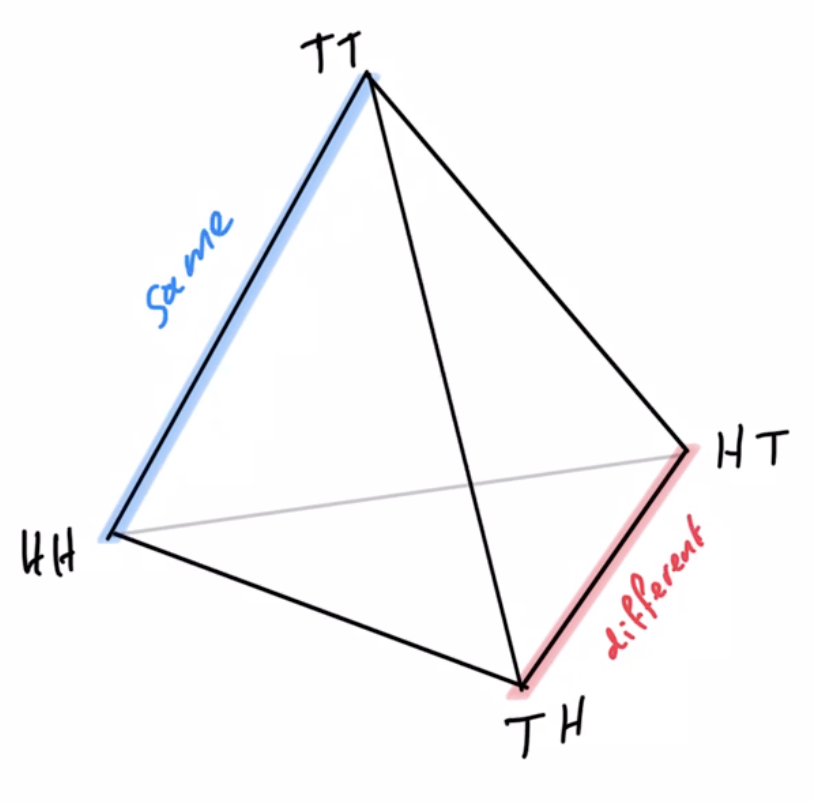
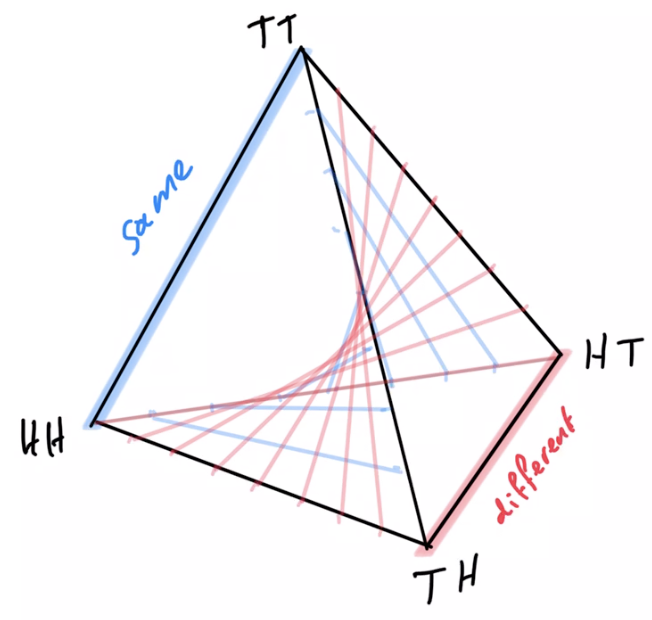
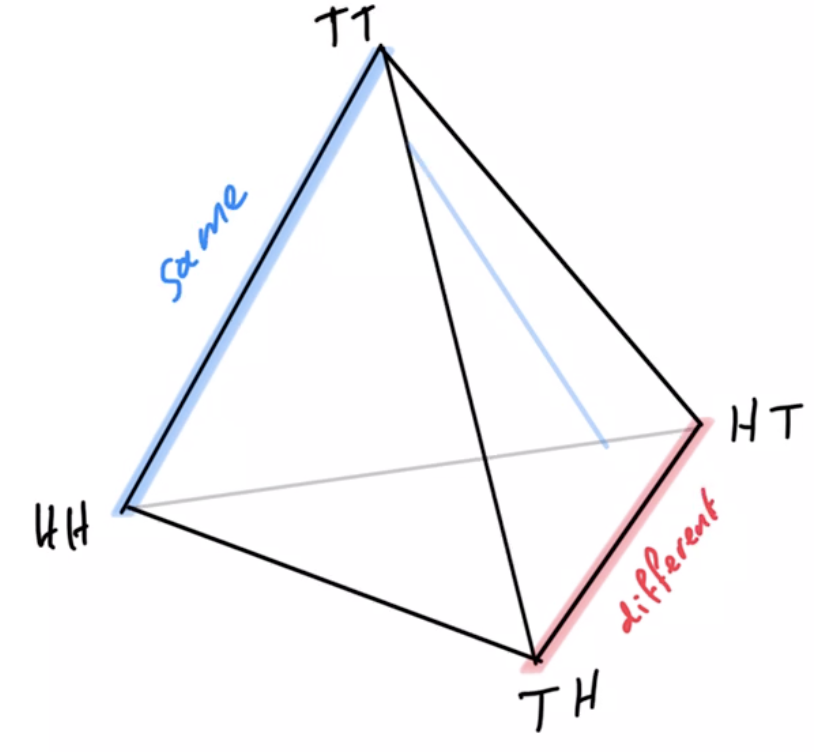
Example non-cooperative game: matching pennies
- Each player \(P_i \in \{1,2\}\) controls a kernel \(p(a_i)\) determining probabilities of heads and tails
- First player wins if both pennies are equal second player wins if they are different
Multi-agent setup
Example non-cooperative game: matching pennies
- Each player \(P_i \in \{1,2\}\) controls a kernel \(p(a_i)\) determining probabilities of heads and tails
- First player wins if both pennies are equal second player wins if they are different
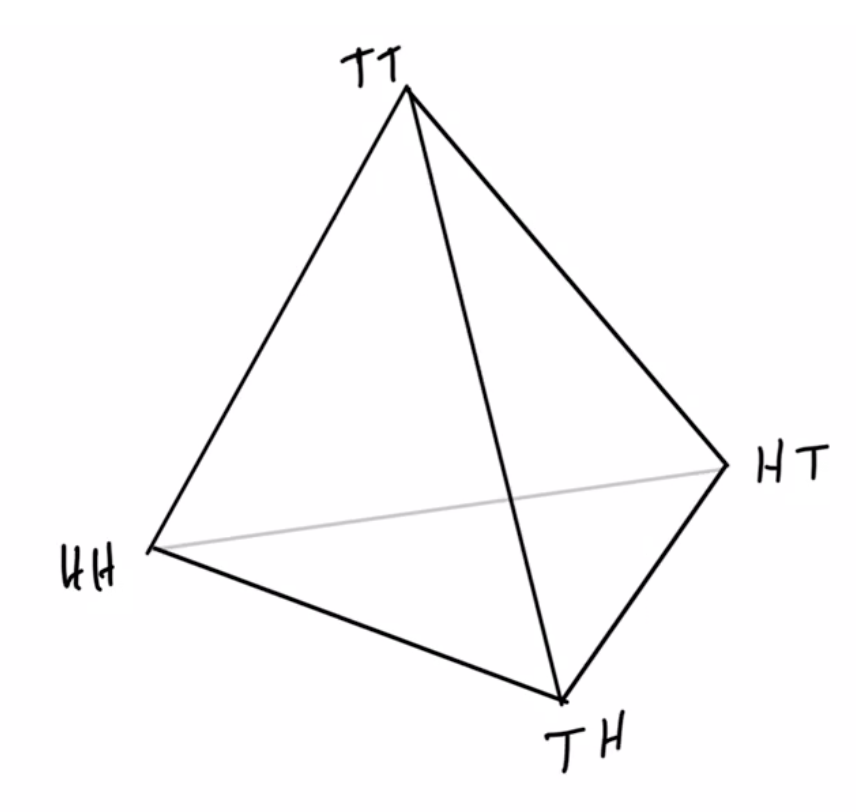
joint pdists \(p(a_1,a_2)\)
disjoint goal manifolds
agent manifold
\(p(a_1,a_2)=p(a_1)p(a_2)\)
Non-cooperative games
- In non-cooperative setting
- instead of maximizing goal probability:
- find Nash equilibria
- can we adapt PAI to do this?
- established that using EM algorithm alternatingly does not converge to Nash equilibria
- other adaptations may be possible...
- instead of maximizing goal probability:
Non-cooperative games
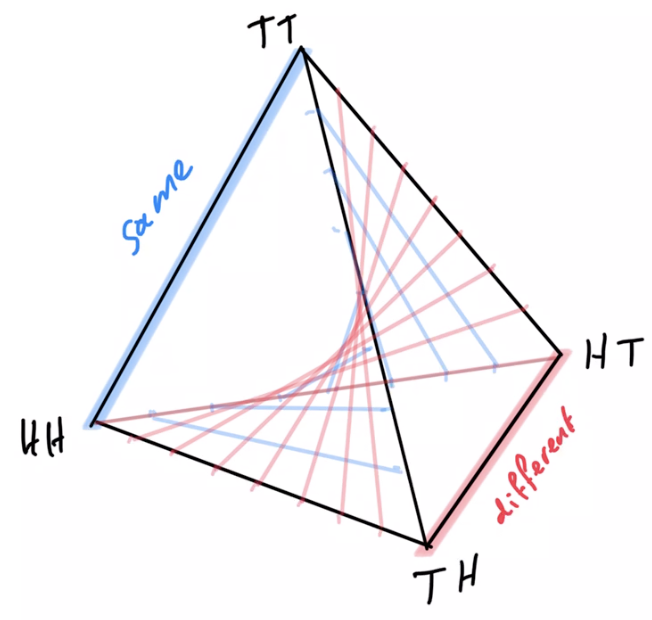
- Counterexample for multi-agent alternating EM convergence:
- Two player game: matching pennies
- Each player \(P_i \in \{1,2\}\) controls a kernel \(p(a_i)\) determining probabilities of heads and tails
- First player wins if both pennies are equal second player wins if they are different
- Two player game: matching pennies

Non-cooperative games
- Counterexample for multi-agent alternating EM convergence:
- Nash equilibrium is known to be both players playing uniform distribution
- Using EM algorithm to fully optimize player kernels alternatingly does not converge
- Taking only single EM steps alternatingly also does not converge
EM
EM

Non-cooperative games
- Counterexample for multi-agent alternating EM convergence
- fix a strategy for player 2 e.g. \(p_0(A_2=H)=0.2\)

Non-cooperative games
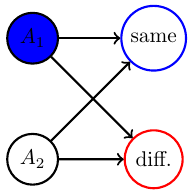
Text
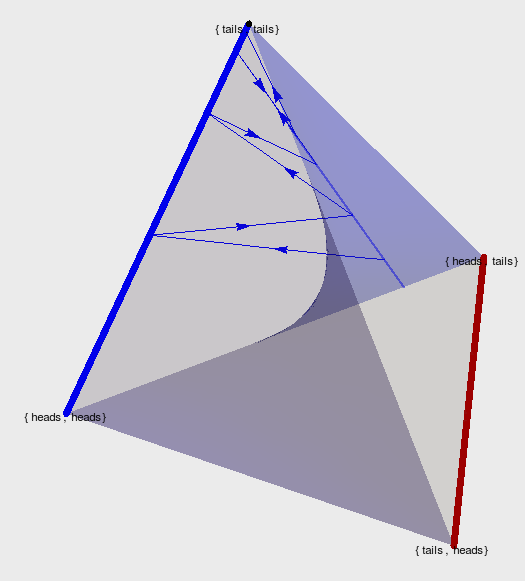
- run EM algorithm for P1
- Ends up on edge from (tails,tails) to (tails,heads)
- result: \(p(A_1=T)=1\)
- then optimizing P2 leads to \(p(A_2=H)=1\)
- then optimizing P1 leads to \(p(A_1=H)=1\)
- and on and on...
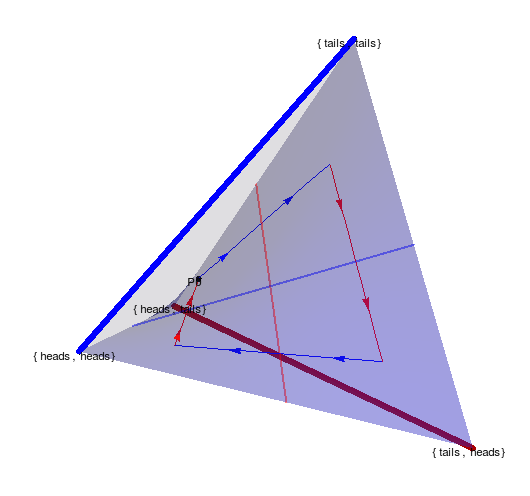
Non-cooperative games
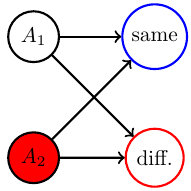
Text
- Taking one EM step for P1 and then one for P2 and so on...
- ...also leads to loop.
Cooperative games
- Concrete example of agent manifold reduction under switch from single agent to multi-agent to identical multi-agent setup
- Like matching pennies but single goal: "different outcome"
- solution: one action/player always plays heads and one always tails
- agent manifold:
- single-agent manifold would be whole simplex
- multi-agent manifold is independence manifold
- multi-agent manifold with shared kernel is submanifold of independence manifold
- Like matching pennies but single goal: "different outcome"
Cooperative games






Multi-agents and games
- Relevance to project:
- dealing with multi-agent and multiple, possibly competing goals is a main goal of the project
- basis for studying communication and interaction
- basis for scaling up number of agents
- basis for understanding advantages of multi-agent setups
Preliminary work
- Implementation of PAI in state of the art software (e.g. using Pyro)
- Planning to learn / uncertain MDP, bandit example.
- Do some agents have no interpretation e.g. the "Absent minded driver"? Collaboration with Simon McGregor.
- Design independence: some problems can be solved even if kernels are chosen independently others require coordinated choice of kernels, some are in between.
- Bayesian networks cannot change their structure dependent on the states of the contained random variables.
Preliminary work
- Implementation of PAI in state of the art software (e.g. using Pyro)
- Proofs of concept coded up in Pyro
- uses stochastic variational inference (SVI) for PAI instead of geometric EM
- may be useful to connect to work with neural networks since based on PyTorch
- For simple cases and visualizations also have Mathematica code
Preliminary work
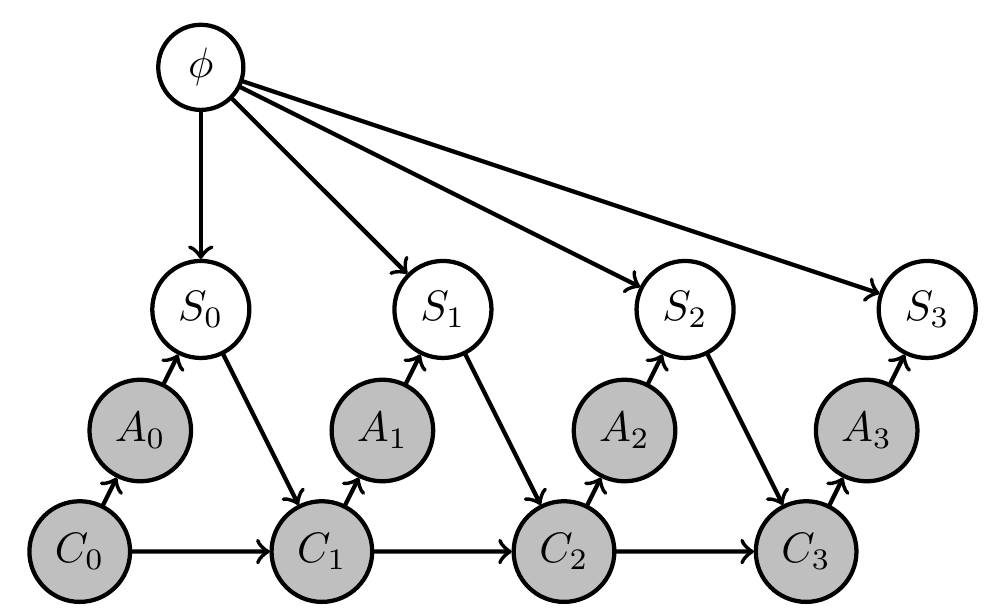
2. Planning to learn / uncertain MDP, bandit example.
- currently investigating PAI for one armed bandit
- goal event is \(G=S_3=1\)
- actions choose one of two bandits that have different win probabilities determined by \(\phi\)
- agent kernels can use memory \(C_t\) to learn about \(\phi\)
Preliminary work
- Do some agents have no interpretation e.g. the "Absent minded driver"? Collaboration with Simon McGregor.
- Driver has to take third exit
- all agent kernels share parameter \(\theta = \)probability of exiting
- optimal is \(\theta= 1/3\)
- Is this an agent even though it may have no consistent intepretation?
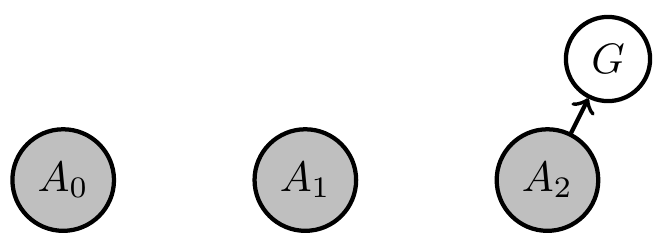
Preliminary work
- Design independence:
- some problems can be solved even if kernels are chosen independently
- others require coordinated choice of kernels,
- some are in between.
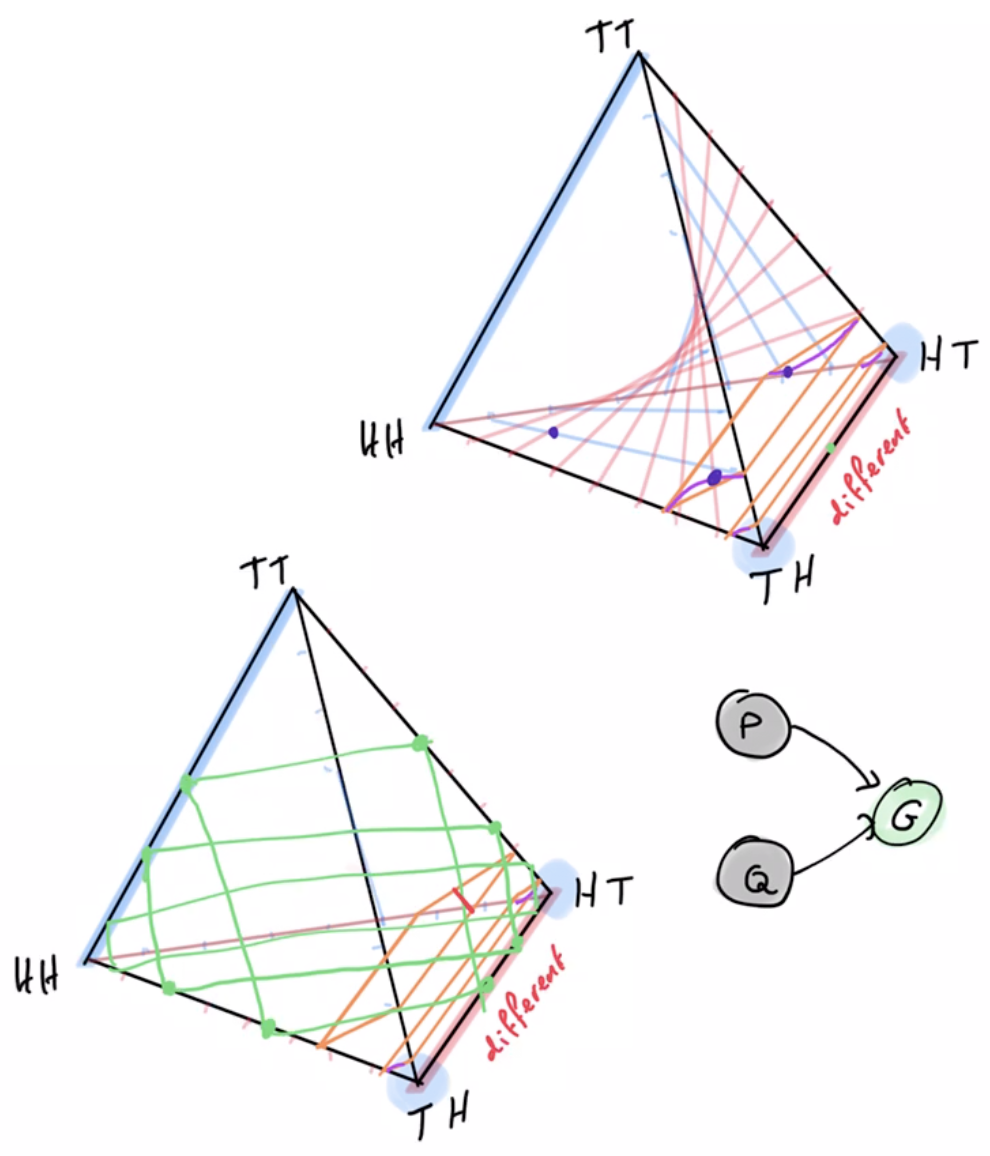
- Two player penny game
- goal is to get different outcomes
- one has to play heads with high probability the other has to play tails
- can't choose two kernels independently
Preliminary work
- Bayesian networks cannot change their structure dependent on the states of the contained random variables.
- Once we fix the (causal) Bayesian network it stays like that ...
if x=1
Preliminary work
- Bayesian networks cannot change their structure dependent on the states of the contained random variables.
- Once we fix the (causal) Bayesian network it stays like that ...

if x=1
But for adding and removing agents probably needed
Preliminary work
- Bayesian networks cannot change their structure dependent on the states of the contained random variables.
- Once we fix the (causal) Bayesian network it stays like that ...
- We are learning about modern ways to deal with such changes dynamically -- polynomial functors.
Thank you for your attention!
Uncertain MDP / RL
- In RL and RL for POMDPs the transition kernels of the environment are considered unknown / uncertain
Two kinds of uncertainty
- Saw before that we can derive policies that deal with uncertainty
- This uncertainty can be seen as the "designer's uncertainty"
- But we can also design agents that have models and come with their own well defined uncertainty
- For those we can turn uncertainty reduction itself into a goal!

Two kinds of uncertainty
- Agent uncertainty:
- e.g. for agent memory implement stochastic world model that updates in response to sensor values
- then by construction each internal state has a well defined associated belief distribution \(ph_t=f(c_t)\) over hidden variables
- turn uncertainty reduction itself into a goal!
- e.g. for agent memory implement stochastic world model that updates in response to sensor values