Second progress report
Martin Biehl and Nathaniel Virgo
- One-slide planning as inference
- Current vision for the project
- Designing agents with planning as inference
- Progress on proposal topics:
- Dynamically changing goals that depend on knowledge acquired
through observations - Multiple, possibly competing goals
- Dynamic scalability of multi-agent systems
- Coordination and communication from an information-theoretic
perspective
- Dynamically changing goals that depend on knowledge acquired
- Bonus section: Planning as inference and Badger
Overview
In nutshell:
- Construct Bayesian network with
- fixed kernels (white)
- controllable (agent) kernels (grey)
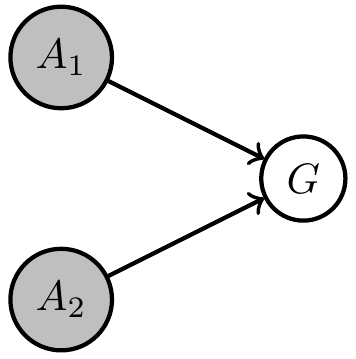
- Goal node (G)
- Find controllable kernels that maximize goal probability.
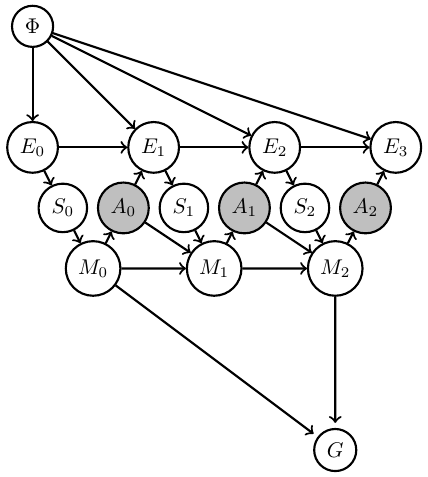
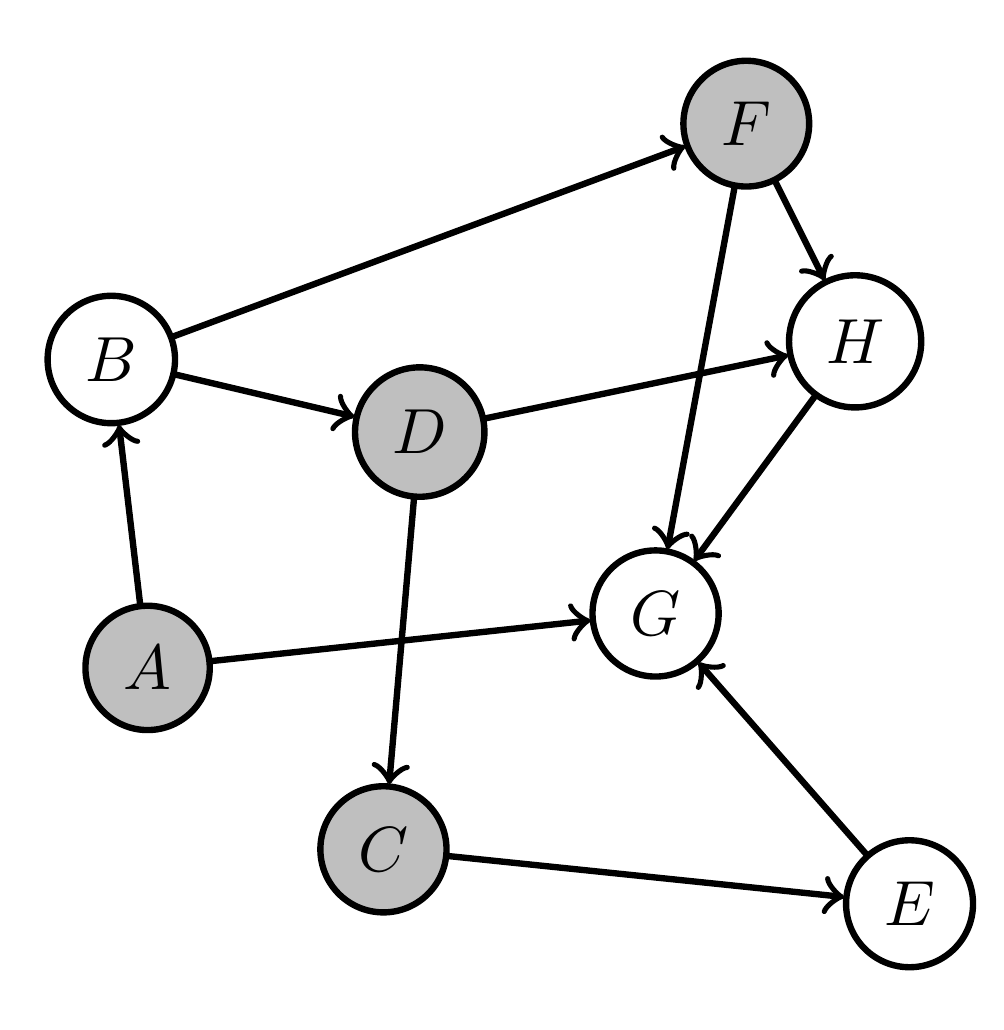
Planning as inference
To find unknown kernels \(p_A:=\{p_a: a \in A\}\)
- "just" maximize probability of achieving the goal:
\[p_A^* = \text{arg} \max_{p_A} p(G=g).\] - automates design of agent memory dynamics and action selection (but hard to solve)

Planning as inference
Planning as inference
Practical side of original framework:
- Represent
- Planning problem structure by Bayesian networks
- Goal and possible policies by sets of probability distributions
- Find policies that maximize probability of goal via geometric EM algorithm.
Bayesian network
goal
policies
Planning as inference
- Problem structures as Bayesian networks:
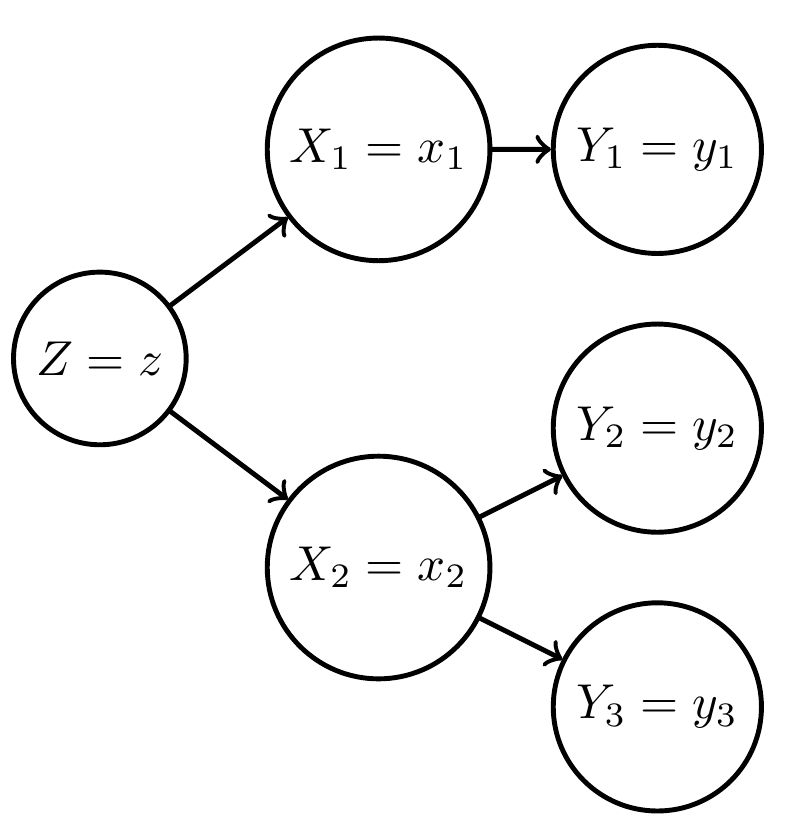
- Let \(V=\{1,...,n\}\) index the nodes in a graph then Bayesian network of random variables \(X=(X_1,..,X_n)\) defines factorized joint probability distribution:
\[\newcommand{\pa}{\text{pa}}p(x) = \prod_{v\in V} p(x_v | x_{\pa(v)}).\] - distinguish:
- fixed nodes \(B\subset V\)
- changeable nodes \(A\subset V\)
- then:
\[\newcommand{\pa}{\text{pa}}p(x) = \prod_{a\in A} p(x_a | x_{\pa(a)}) \, \prod_{b\in B} \bar p(x_b | x_{\pa(b)})\]
- Let \(V=\{1,...,n\}\) index the nodes in a graph then Bayesian network of random variables \(X=(X_1,..,X_n)\) defines factorized joint probability distribution:
Planning as inference
- Problem structures as Bayesian networks:
Planning as inference

Bayesian network
goal
- Represent goals and policies by sets of probability distributions:
-
goal must be an event i.e. function \(G(x)\) with
- \(G(x)=1\) if goal is achieved
- \(G(x)=0\) else.
-
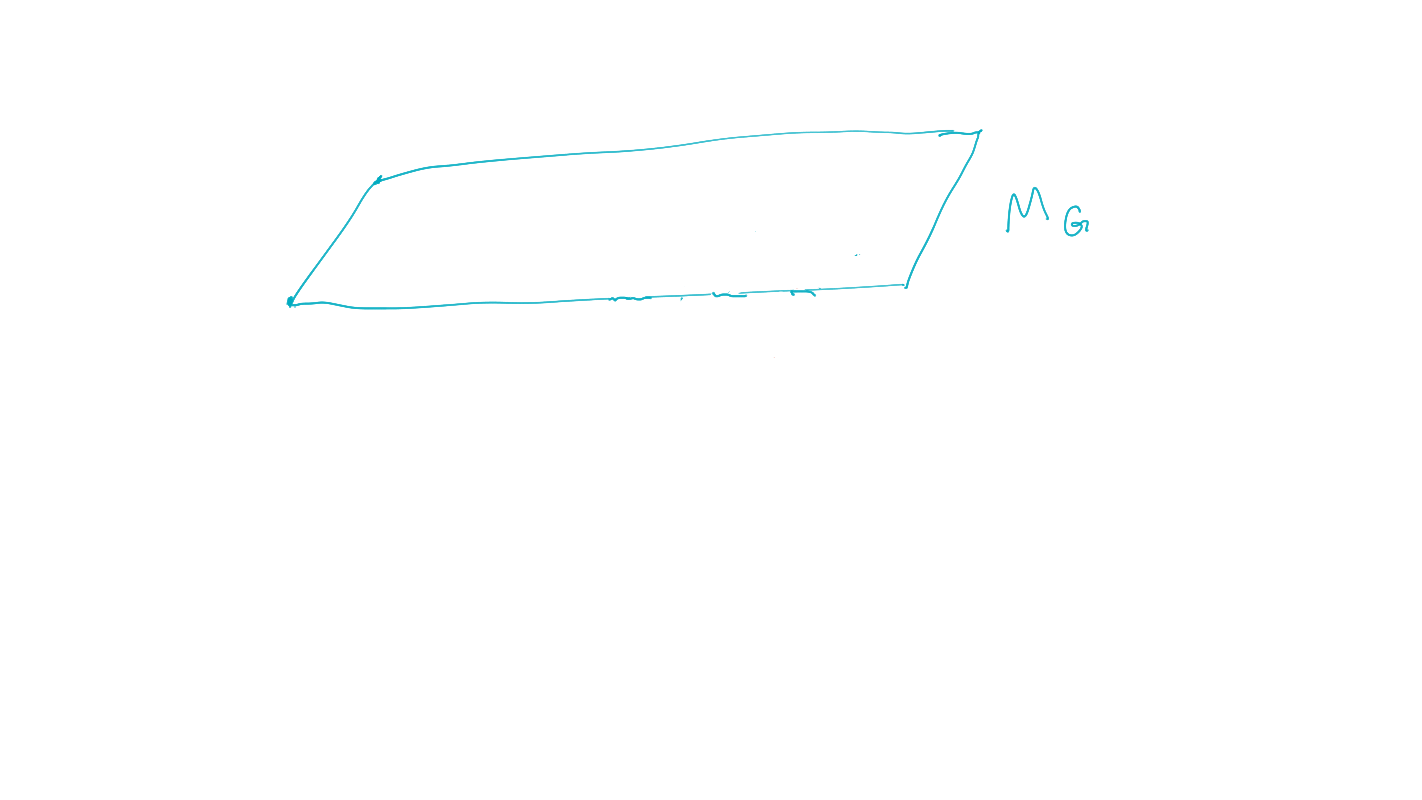
goal manifold is set of distributions where the goal event occurs with probability one:
\[M_G:=\{P: p(G=1)=1\}\]
-
goal must be an event i.e. function \(G(x)\) with
Planning as inference
- Represent goals and policies by sets of probability distributions:
-
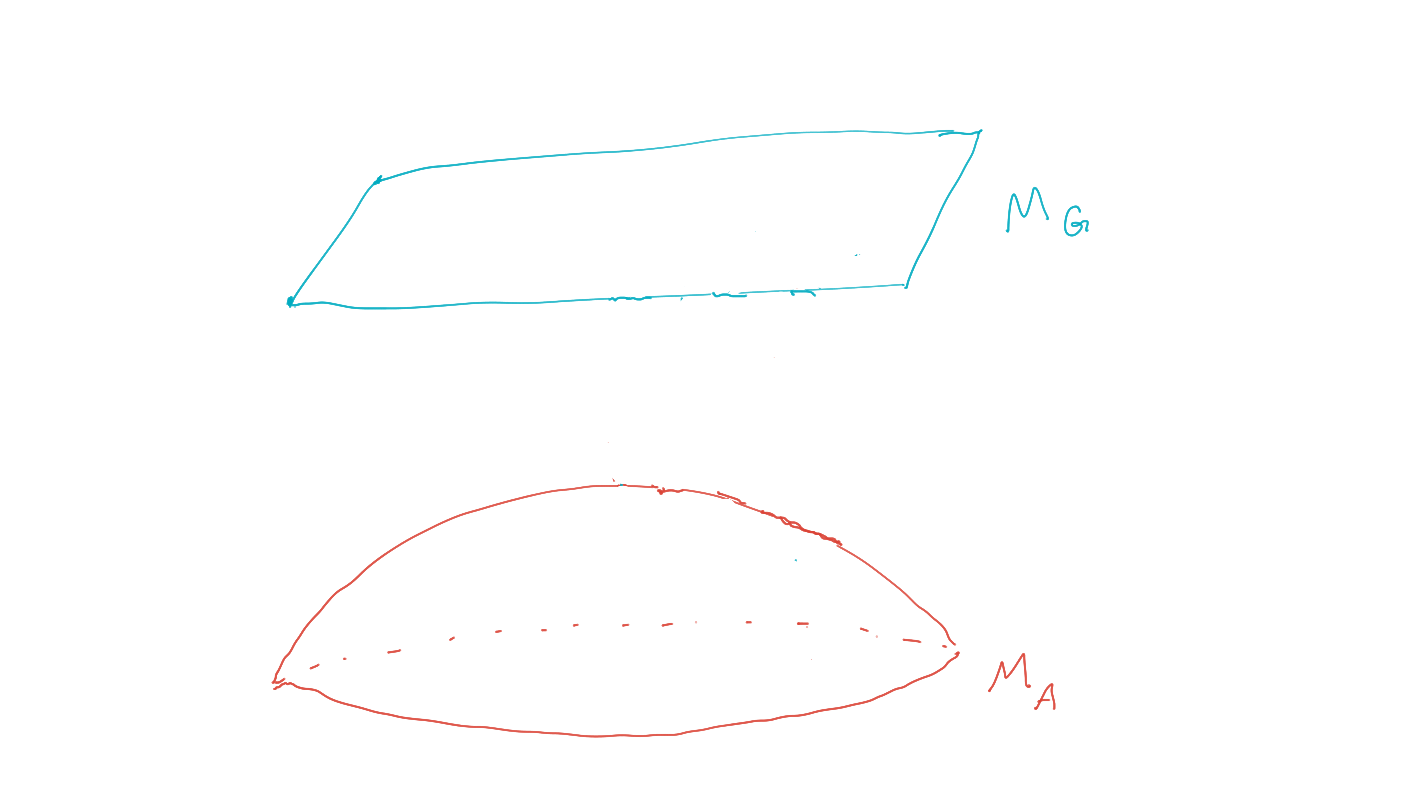
policy is a choice of the changeable Markov kernels
\[\newcommand{\pa}{\text{pa}}\{p(x_a | x_{\pa(a)}):a \in A\}\] -
agent manifold/policy manifold is set of distributions that can be achieved by varying policy
\[\newcommand{\pa}{\text{pa}}p(x) = \prod_{a\in A} p(x_a | x_{\pa(a)}) \, \prod_{b\in B} \bar p(x_b | x_{\pa(b)})\]
-
policy is a choice of the changeable Markov kernels

Bayesian network
goal
policies
Planning as inference
- Find policies that maximize probability of goal via geometric EM algorithm:
-
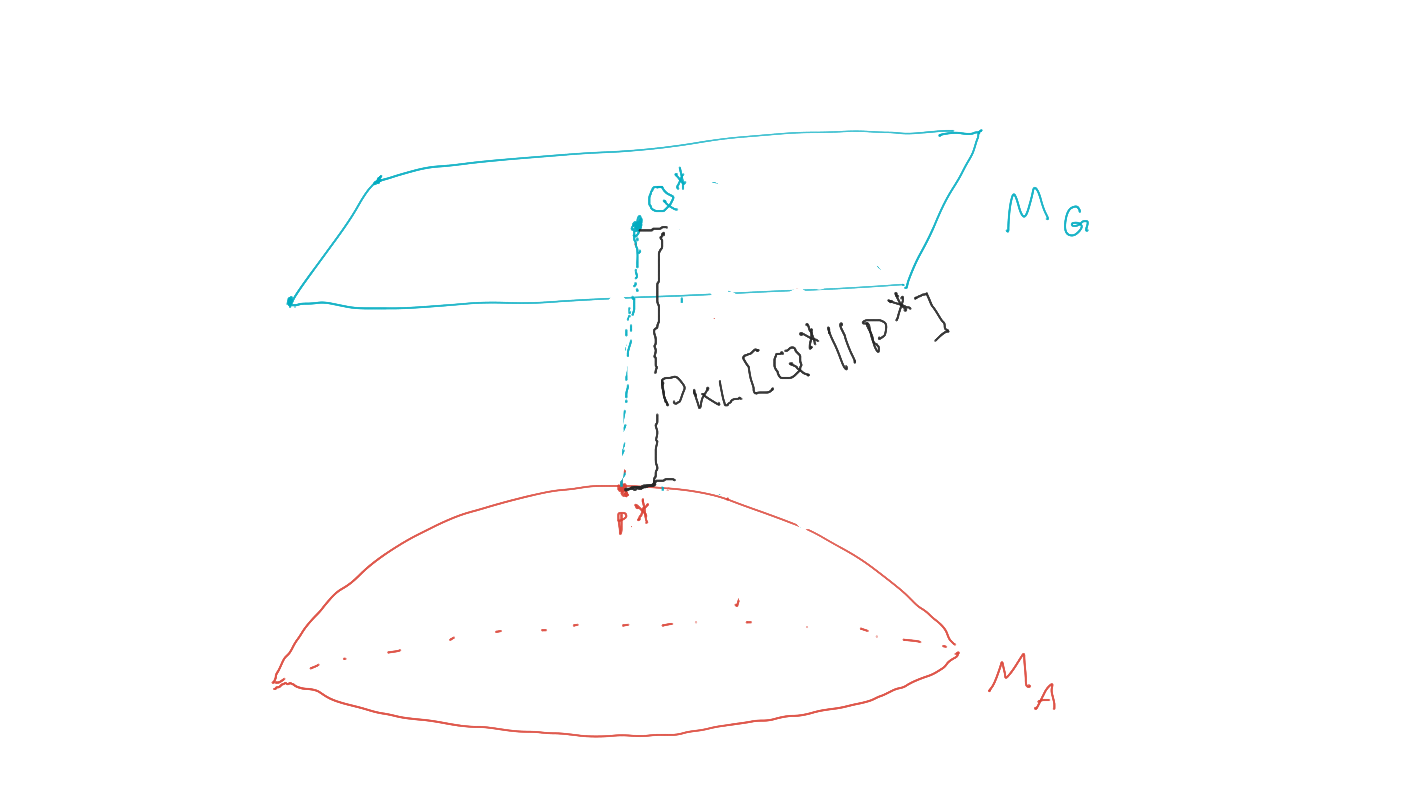
planning as inference finds policy / agent kernels such that:
\[P^* = \text{arg} \max_{P \in M_A} p(G=1).\] - (compare to maximum likelihood inference)
-
planning as inference finds policy / agent kernels such that:

Bayesian network
goal
policies

Planning as inference
- Find policies that maximize probability of goal via geometric EM algorithm:
- Can prove that \(P^*\) is the distribution in agent manifold closest to goal manifold in terms of KL-divergence
- Local minimizers of this KL-divergence can be found with the geometric EM algorithm

Bayesian network
goal
policies
Planning as inference
- Find policies that maximize probability of goal via geometric EM algorithm:
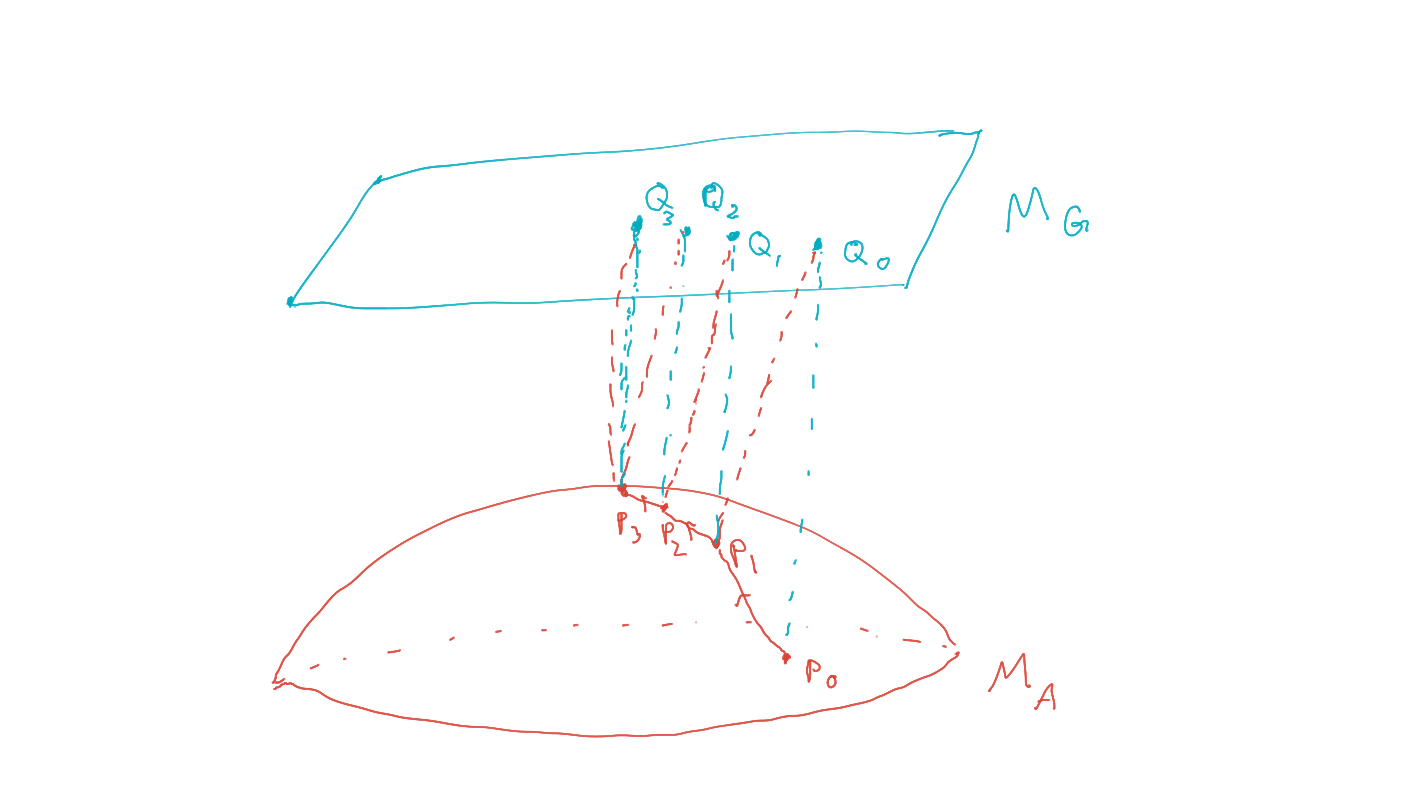
- Start with an initial prior, \(P_0 \in M_A\) .
- (e-projection)
\[Q_t = \text{arg} \min_{Q\in M_G} D_{KL}(Q∥P_t )\] - (m-projection)
\[P_{t+1} = \text{arg} \min_{P \in M_A} D_{KL} (Q_t ∥P )\]


Bayesian network
goal
policies
Planning as inference
- Find policies that maximize probability of goal via geometric EM algorithm:
- Equivalent algorithm using only marginalization and conditioning:
- Initial agent kernels define prior, \(P_0 \in M_A\).
- Get \(Q_t\), from \(P_t\) by conditioning on the goal: \[q_t(x) = p_t(x|G=1).\]
- Get \(P_{t+1}\), by replacing agent kernels by conditional distributions in \(Q_t\):
\[\newcommand{\pa}{\text{pa}} p_{t+1}(x) = \prod_{a\in A} q_t(x_a | x_{\pa(a)}) \, \prod_{b\in B} \bar p(x_b | x_{\pa(b)})\]
\[\newcommand{\pa}{\text{pa}} \;\;\;\;\;\;\;= \prod_{a\in A} p_t(x_a | x_{\pa(a)},g) \, \prod_{b\in B} \bar p(x_b | x_{\pa(b)})\]
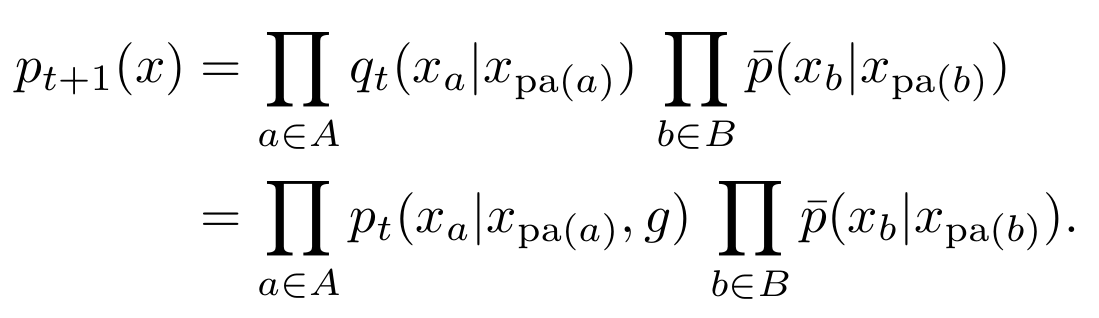
Current vision for the project

- view PAI as (incomplete) theory of designing intelligent agents
- allows formulating problems whose solutions are intelligent agents
- use and extend PAI to understand
- formation of single agent out of multiple agents
- advantages of multi-agent systems
- advantages of dynamically changing agent numbers



Designing artificial agents
Use planning as inference for agent design:
Note: Bayesian network structure of
- fixed kernels expresses/defines structure of problem
- controllable kernels expresses/defines structure of solutions
Controllable kernel structure can be used to make internal structure of designed agent explicit!

Designing artificial agents
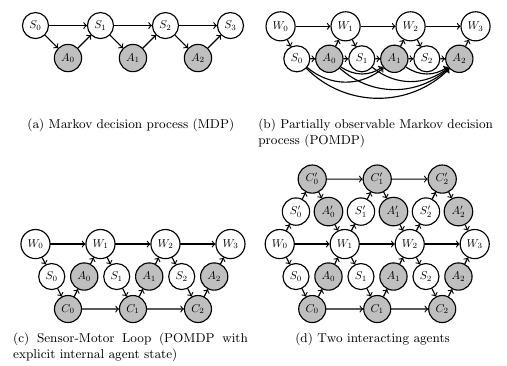
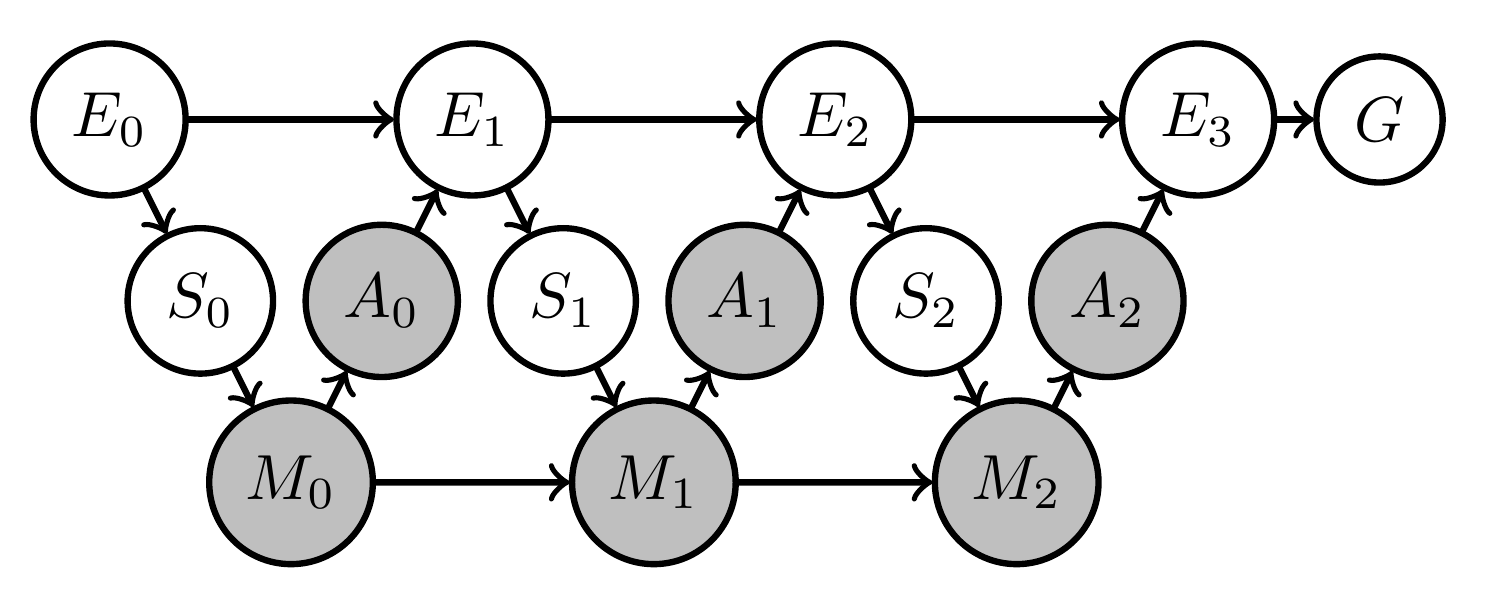
Consider designing an artificial agent for a POMDP i.e. you know
- dynamics of environment \(E\) the agent will face
- sensor values \(S\) available to it
- actions \(A\) it can take
- goal \(G\) (or reward) it should achieve
Then find
- kernels that produce actions \(A_t\)
- maximize goal probability
via planning as inference.

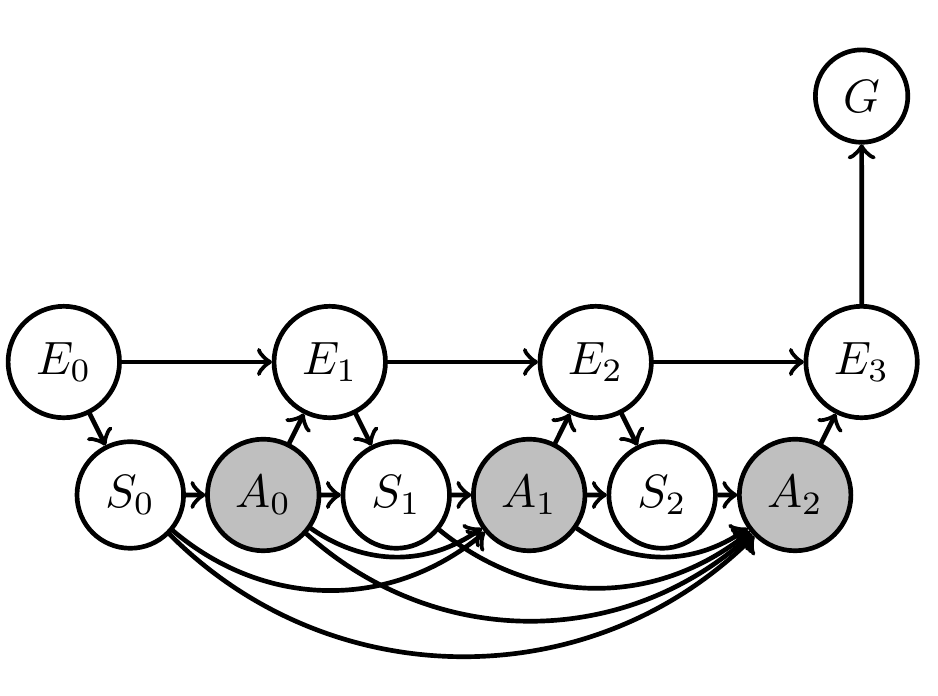
Designing artificial agents
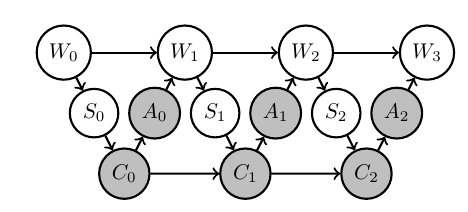
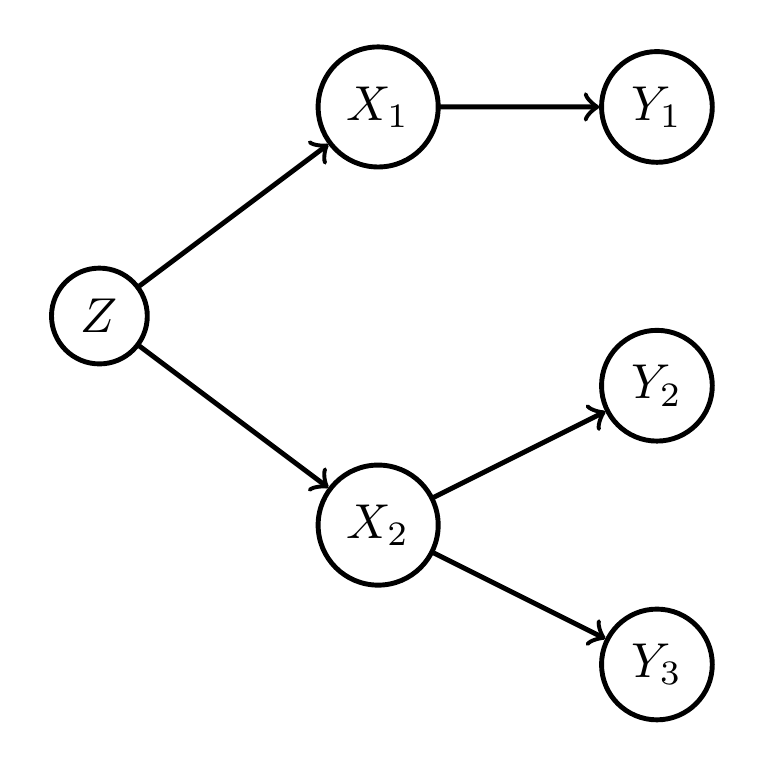
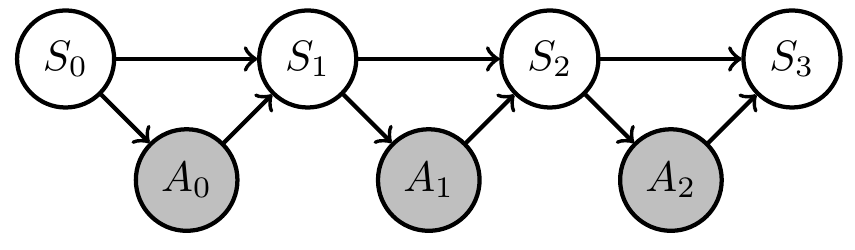
Get three kernels:
- \(p(a_0|s_0)\)
- \(p(a_1|s_0,a_0,s_1)\)
- \(p(a_2|s_0,a_0,s_1,a_1,s_2)\)
But in practice (on a robot) time passes between \(S_0\) and \(A_2\):
- if \(A_2\) depends on \(S_0\)
- have to store \(S_0\)
- but where?


Text
Designing artificial agents
Action maybe produced by three kernels:
- \(p(a_0|s_0)\)
- \(p(a_1|s_0,a_0,s_1)\)
- \(p(a_2|s_0,a_0,s_1,a_1,s_2)\)
In practice time passes between \(S_0\) and \(A_2\):
- if \(A_2\) depends on \(S_0\)
- have to store \(S_0\)
So also need to find
- dynamics of memory \(M\)
Also want constant memory and action kernels
- \(p(m_{t_1}|s_{t_1},m_{t_1-1})=p(m_{t_2}|s_{t_2},m_{t_2-1})\)

Designing artificial agents
In following "agent" usually means
- two Markov kernels
- memory update \[p(m_t|s_t,m_{t-1})\]
- action selection \[p(a_t|m_t)\]
- constant over time (if there is time)
\[p(m_{t_1}|s_{t_1},m_{t_1-1})=p(m_{t_2}|s_{t_2},m_{t_2-1})\]
\[p(a_{t_1}|m_{t_1})=p(a_{t_2}|m_{t_2})\] - (formally: use shared parameters...)

Two situations:
- designer uncertain about environment dynamics
- agent supposed to deal with different environments
Explicitly reflect either by
- additional variable \(\phi\)
- prior distribution over \(\phi\)
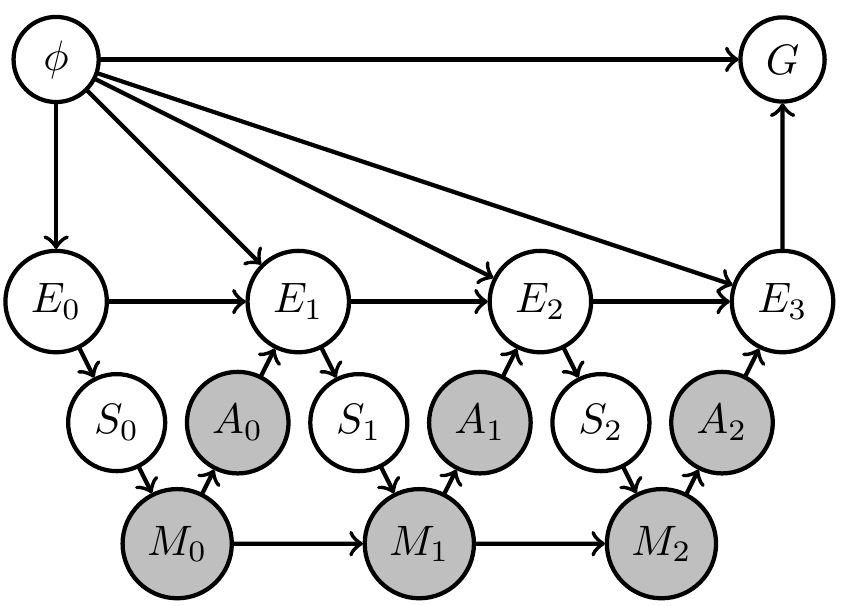
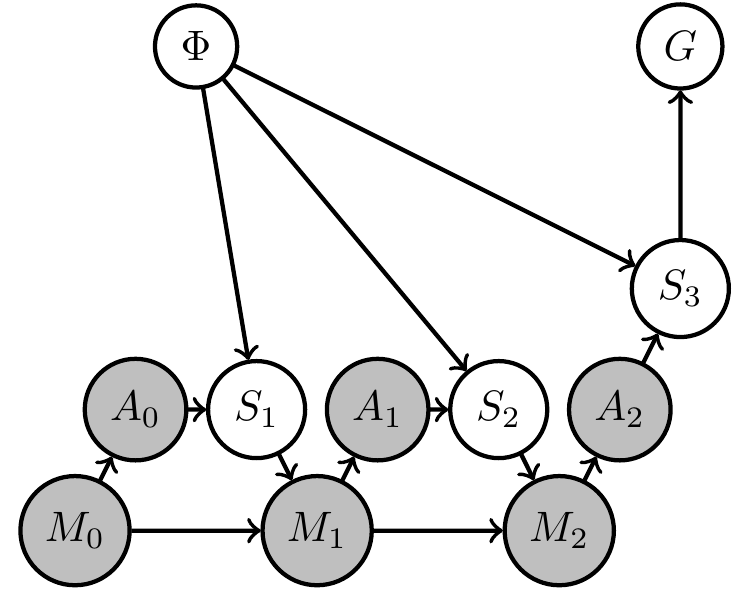
Application: Designer uncertainty


Then
- resulting agent will find out what is necessary to achieve goal
- i.e. it will trade off exploration (try out different arms) and exploitation (winning)
- comparable to meta-learning


Application: Designer uncertainty
Example: 2-armed bandit
- Constant hidden "environment state" \(\phi=(\phi_1,\phi_2)\) storing win probabilities of two arms
- agent action is choice of arm \(a_t \in \{1,2\}\)
- sensor value is either win or lose sampled according to win probability of chosen arm \(s_t \in \{\text{win},\text{lose}\}\)
\[p_{S_t}(s_t|a_{t-1},\phi)=\phi_{a_{t-1}}^{\delta_{\text{win}}(s_t)} (1-\phi_{a_{t-1}})^{\delta_{\text{lose}}(s_t)}\] - goal is achieved if last arm choice results in win \(s_3=\text{win}\)
\[p_G(G=1|s_3)=\delta_{\text{win}}(s_3)\] - memory \(m_t \in \{1,2,3,4\}\) is enough to store all different results.
Progress on proposal topics
- Two (or more?) possibilities:
- creation of "genuinely new" goals
- one single goal that depends on knowledge but drives acquisition of more knowledge (and maybe new "subgoals") indefinitely
- Here focus on the latter.
Dynamically changing goals that depend on knowledge acquired
through observations
Dynamically changing goals
Consider agent that solves a problem in uncertain environment.
- would expect that such agent acquires some "knowledge" during interaction with environment
- but can we extract it?
- maybe there is a kind of minimal required knowledge that an agent must have to solve the problem?
- we don't know yet...



Alternatively:
- construct (part of) memory update function
- guarantee existence of notion of knowledge e.g. Bayesian beliefs

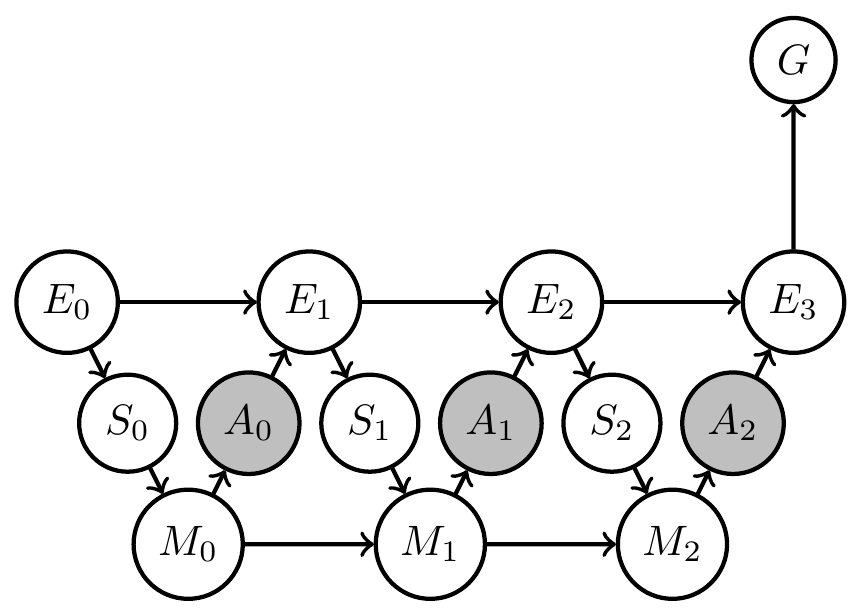
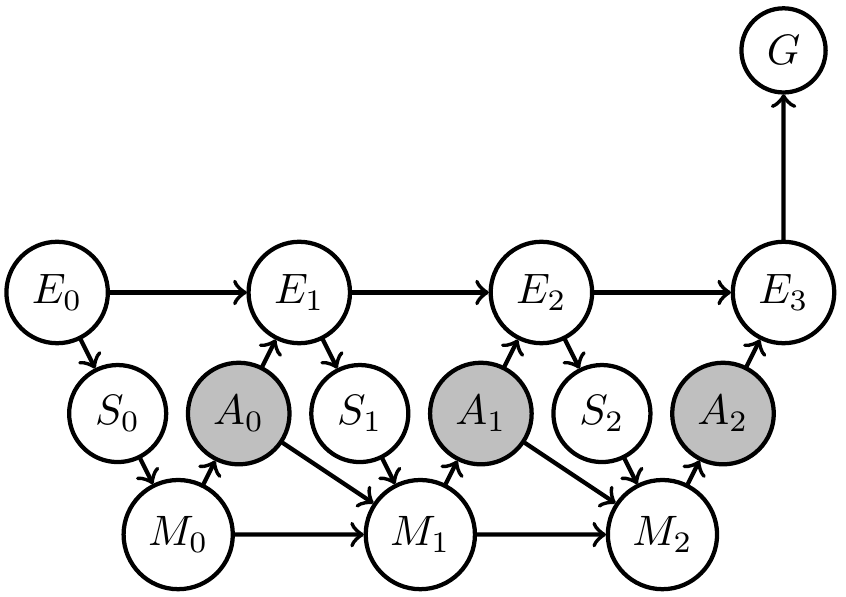
Dynamically changing goals
Interpreting systems a Bayesian reasoners
Recall Bayes rule (for any random variables \(A,B\)):
\[p(b\,|\,a) = \frac{p(a\,|\,b)}{p(a)} \;p(b)\]
- where
\[p(a) = \sum_b p(a\,|\,b)\;p(b)\] - if we know \(p(a\,|\,b)\) and \(p(b)\) we can compute \(p(b\,|\,a)\)
- nice.
Interpreting systems a Bayesian reasoners
Bayesian inference:
- parameterized model: \(p(x|\theta)\)
- prior belief over parameters \(p(\theta)\)
- observation / data: \(\bar x\)
- Then according to Bayes rule:
\[p(\theta|x) = \frac{p(x|\theta)}{p(x)} p(\theta)\]
Interpreting systems a Bayesian reasoners
Bayesian belief updating:
- introduce time steps \(t\in \{1,2,3...\}\)
- initial belief \(p_1(\theta)\)
- sequence of observations \(x_1,x_2,...\)
- use Bayes rule to get \(p_{t+1}(\theta)\):
\[p_{t+1}(\theta) = \frac{p(x_t|\theta)}{p_t(x_t)} p_t(\theta)\]
Interpreting systems a Bayesian reasoners
Bayesian belief updating with conjugate priors:
- now parameterize the belief
using the "conjugate prior" for model \(p(x|\theta)\)
\[p_1(\theta) \mapsto p(\theta|\alpha_1) \] - \(\alpha\) are called hyperparameters
- plug this into Bayesian belief updating:
\[p(\theta|\alpha_{t+1}) = \frac{p(x_t|\theta)}{p(x_t|\alpha_t)} p(\theta|\alpha_t)\]
where \(p(x_t|\alpha_t) := \int_\theta p(x_t|\theta)p(\theta|\alpha_t) d\theta\) - So what?
Interpreting systems a Bayesian reasoners
Bayesian belief updating with conjugate priors:
- well then: there exists a hyperparameter translation function \(f\) such that
\[\alpha_{t+1} = f(x,\alpha_t)\] - maps current hyperparameter \(\alpha_t\) and observation \(x\) to next hyperparameter \(\alpha_{t+1}\)
- but beliefs are determined by the hyperparamter!
- we can always recover them (if we want) but for computation we can forget all the probabilities!
\[p(\theta|f(x_t,\alpha_t)) = \frac{p(x_t|\theta)}{p(x_t|\alpha_t)} p(\theta|\alpha_t)\]
Interpreting systems a Bayesian reasoners
Bayesian belief updating with conjugate priors:
- so if we have a conjugate prior we can implement Bayesian belief updating with a function
\[f:X \times \mathcal{A} \to \mathcal{A}\]
\[\alpha_{t+1}= f(x,\alpha_t)\] - this is just a (discrete time) dynamical system with inputs
- Interpreting systems as Bayesian reasoners just turns this around!
Interpreting systems a Bayesian reasoners
- given discrete dynamical system with input defined by
\[\mu: S \times M \to M\]
\[m_{t+1}=\mu(s_t,m_t)\] - a consistent Bayesian inference interpretation is:
- interpretation map \(\psi(\theta|m)\)
- model \(\phi(s|\theta)\)
- such that the dynamical system acts like a hyperparameter translation function i.e. if:
\[\psi(\theta|\mu(s_t,m_t)) = \frac{\phi(s_t|\theta)}{(\phi \circ \psi)(s_t|m_t)} \psi(\theta|m_t)\]
One way:
- choose model of causes of sensor values for agent
- fix memory update \(p(m_t|s_t,m_{t-1})\) to have consistent Bayesian interpretation w.r.t chosen model (e.g. use hyperparameter translation function for conjugate prior)
- only action kernels \(p_A(a_t|m_t)\) unknown



Dynamically changing goals
Then by construction
- know a consistent Bayesian interpretation
- i.e.\ an interpretation map \(\psi:M \to PH\)
- well defined agent uncertainty in state \(m_t\) via Shannon entropy \[H_{\text{Shannon}}(m_t):=-\sum_{h} \psi(h||m_t) \log \psi(h||m_t)\]
- information gain from \(m_0\) to \(m_t\) by KL divergence \[D_{\text{KL}}[m_t||m_0]:=\sum_h \psi(h||m_t) \log \frac{\psi(h||m_t)}{\psi(h||m_0)}\]
Dynamically changing goals
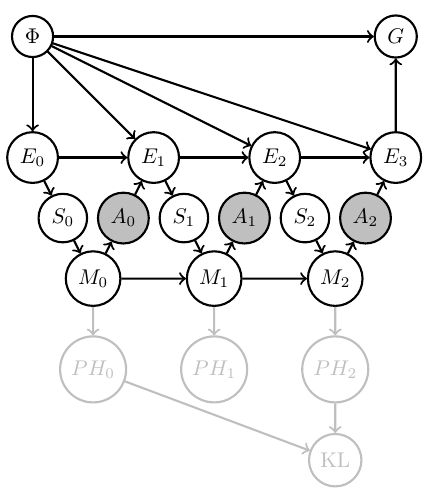
Note:
- can then also turn this information gain into a goal to create intrinsically motivated agent
- from report:
Dynamically changing goals

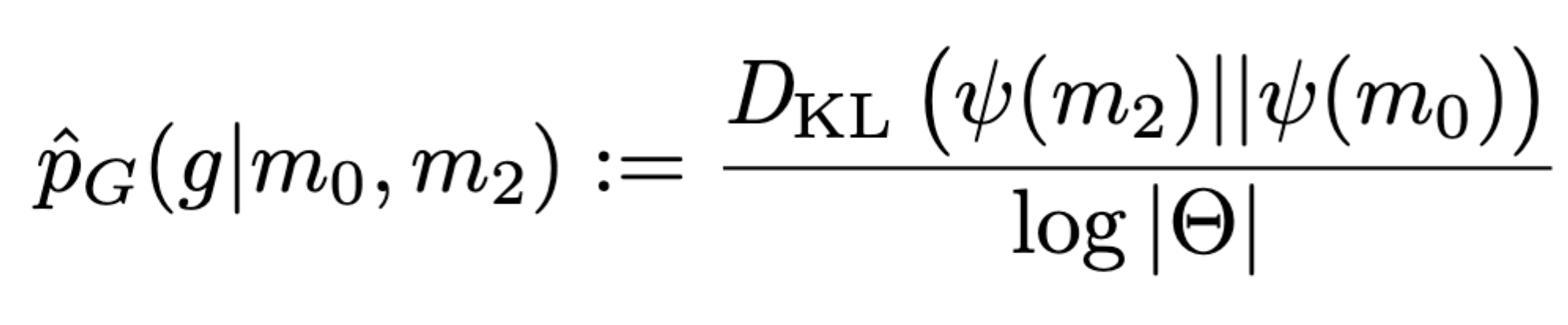
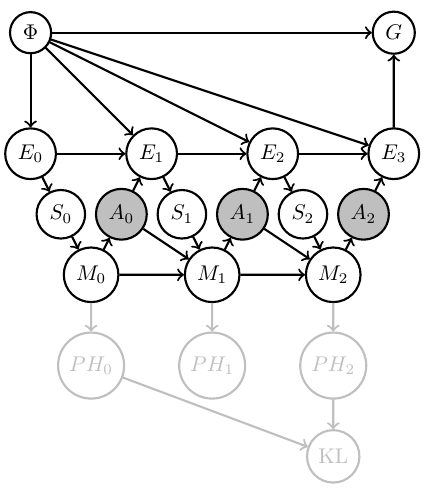
Designing artificial agents
Consider agent that solves a problem in uncertain environment.
- but if we construct (part of) the memory update function then we can guarantee the existence of a notion of knowledge e.g. Bayesian beliefs
- this gives us a way to turn expected information gain maximization into a goal.



Note:
- additional non-fixed memory could be added
- to get indefinite knowledge increase need extension to infinite time
- VAE world models approximate Bayesian consistency and can also be used for information gain
Dynamically changing goals



Multiple, possibly competing goals

- want to harness power of collectives
- both collaboration and competition may be beneficial for collective
- to understand possibilities consider incompatible goals -> game theory
- problems can be expressed using multiple goal nodes
- solving them can be hard (we found out and it is known)
- when and why which algorithm works to be seen
- (may shed light on why GANs work)
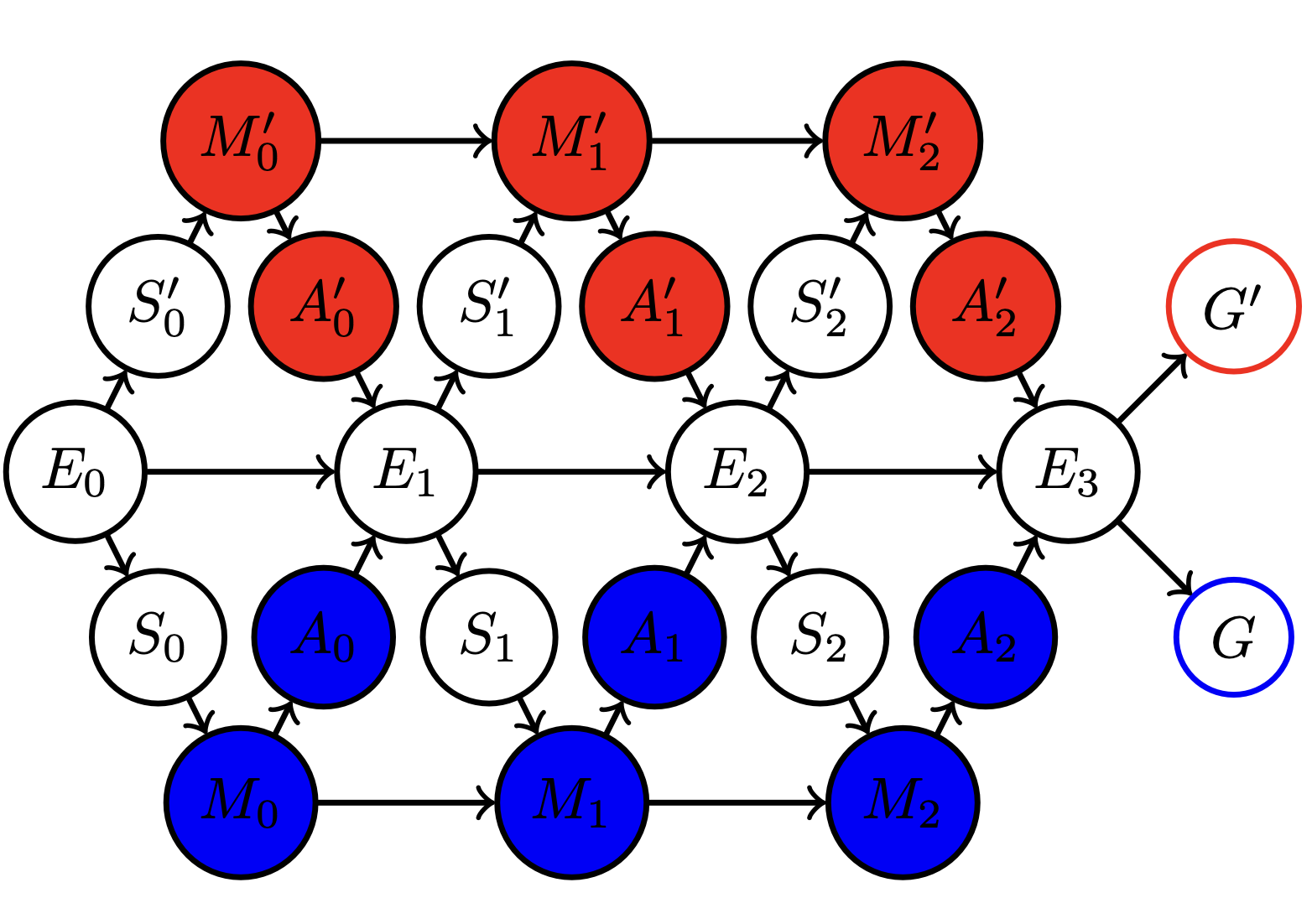
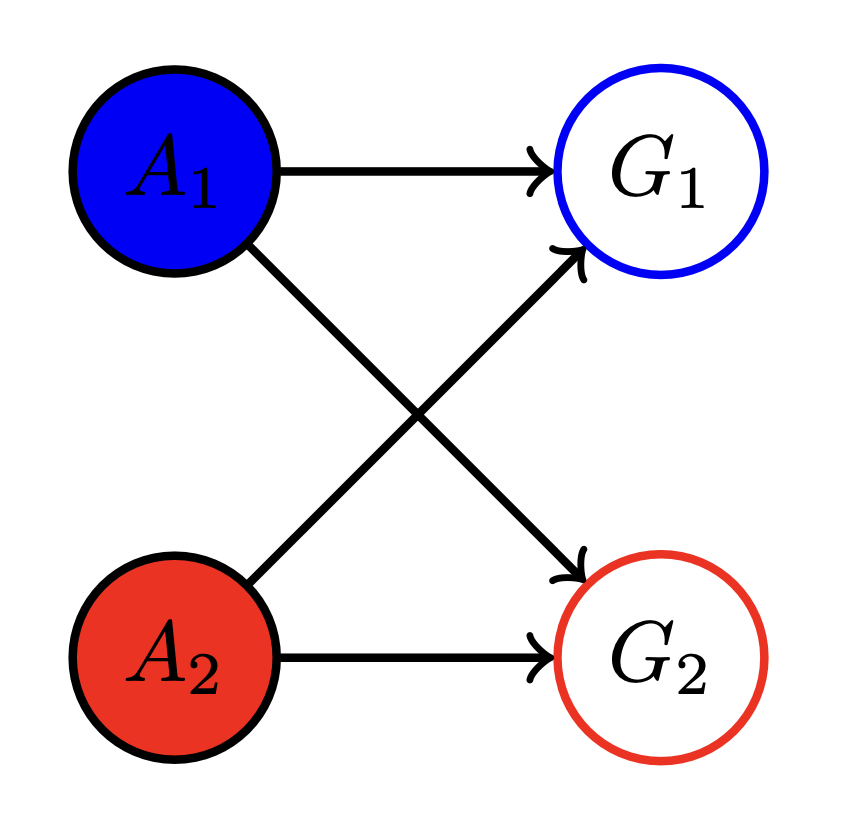
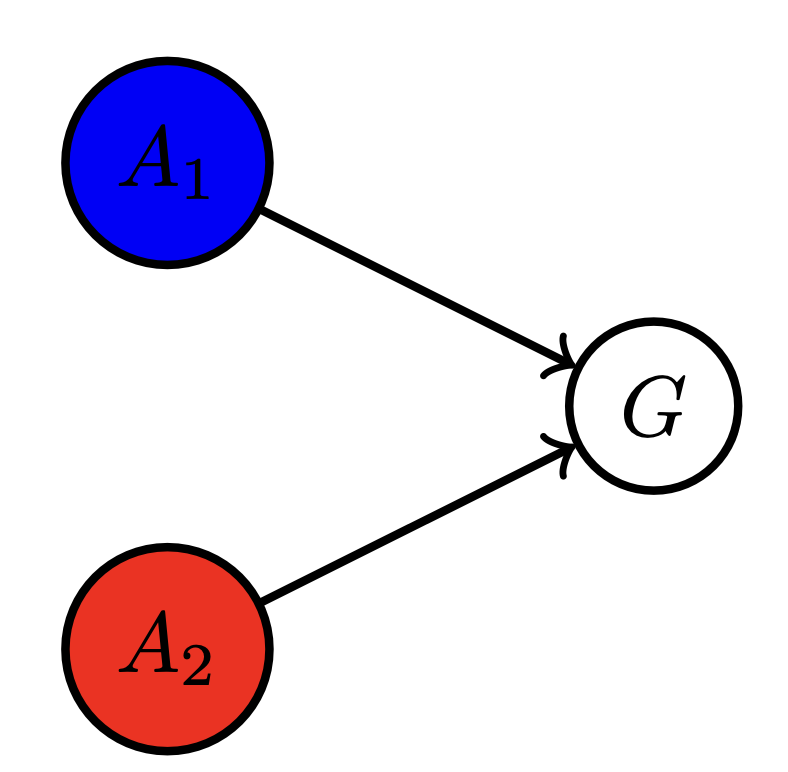
Multi-agent setup
Example multi agent setups:
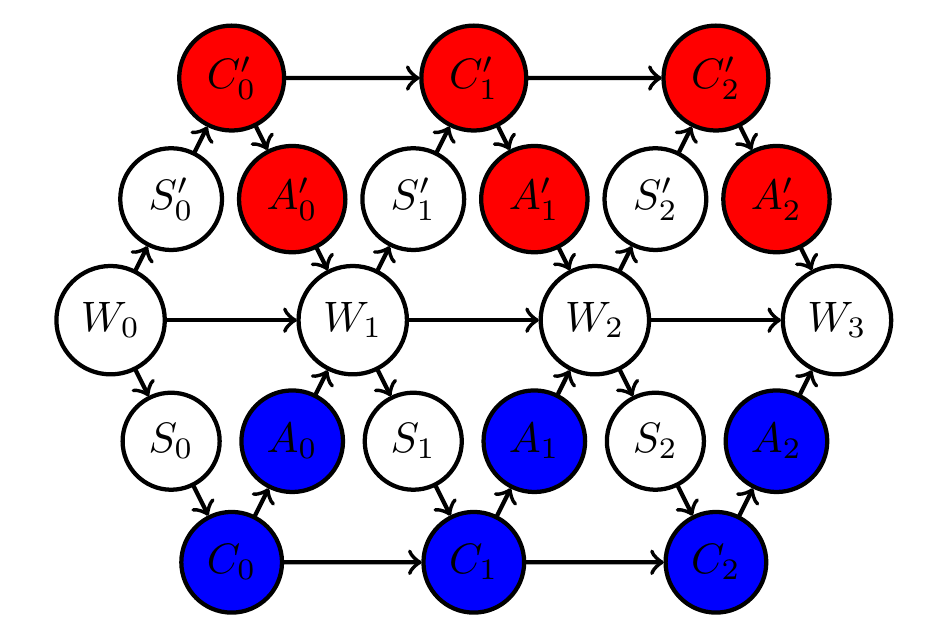
Two agents interacting with same environment
Two agents with same goal
Two agents with different goals
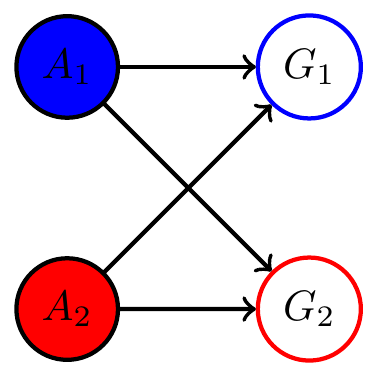
Multi-agent setup
- Note:
- In cooperative setting:
- can often combine multiple goals to single common goal via event intersection, union, complement (supplied by \(\sigma\)-algebra)
- single goal manifold
- in principle can use single agent PAI as before
- In cooperative setting:


Multi-agent setup
- Note:
- In non-cooperative setting:
- goal events have empty intersection
- no common goal
- multiple disjoint goal manifolds
- goal events have empty intersection
- In non-cooperative setting:

Multi-agent setup
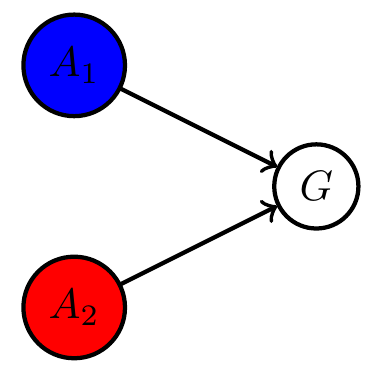
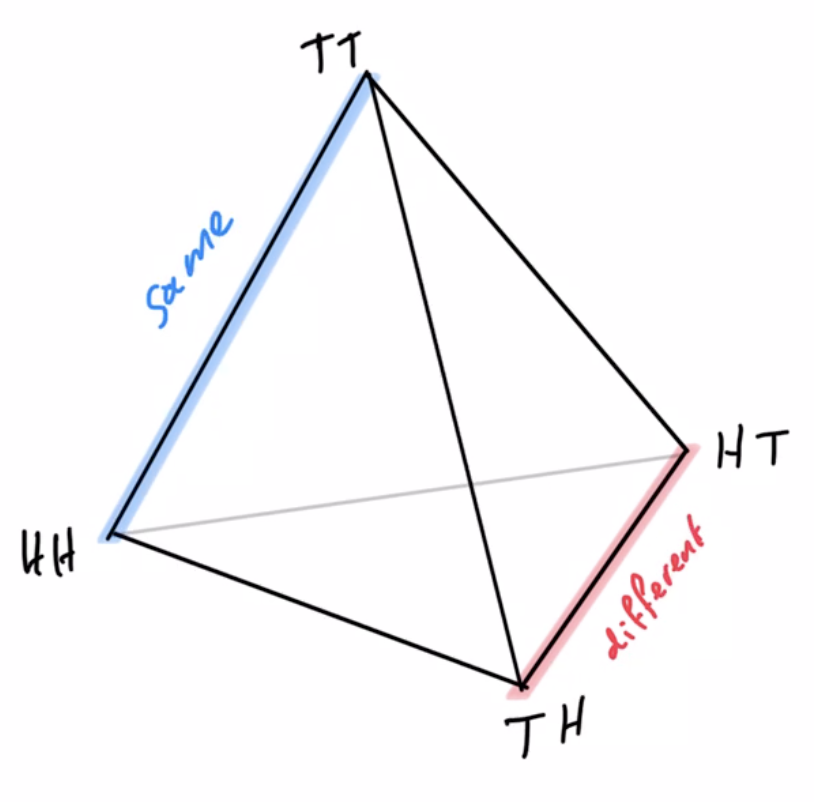
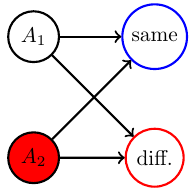
Example non-cooperative game: matching pennies
- Each player \(P_i \in \{1,2\}\) controls a kernel \(p(a_i)\) determining probabilities of heads and tails
- First player wins if both pennies are equal second player wins if they are different
Multi-agent setup
Example non-cooperative game: matching pennies
- Each player \(P_i \in \{1,2\}\) controls a kernel \(p(a_i)\) determining probabilities of heads and tails
- First player wins if both pennies are equal second player wins if they are different
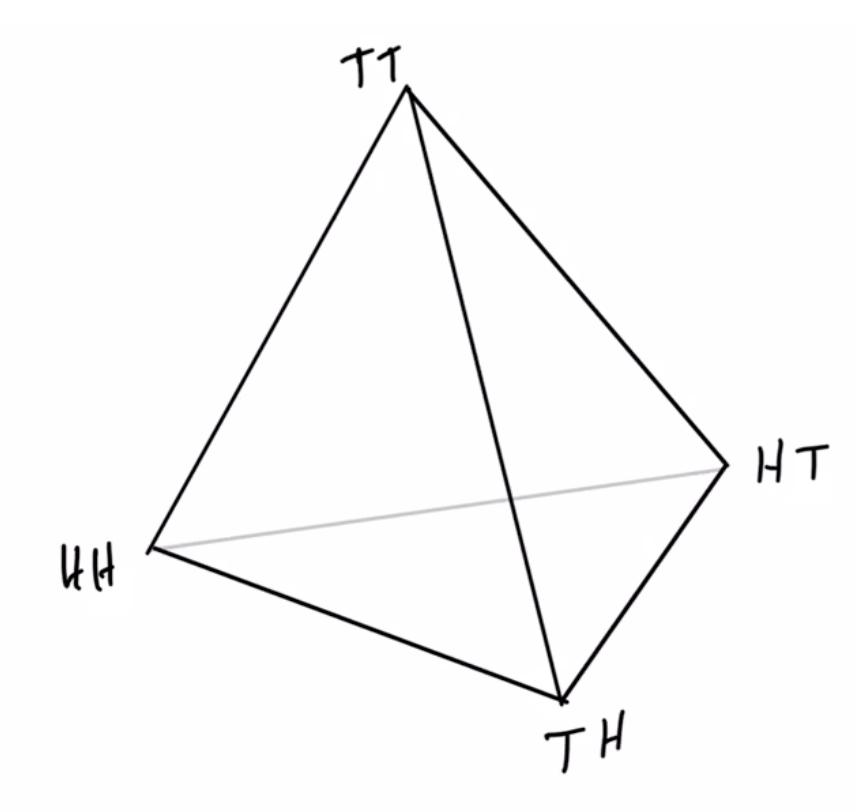
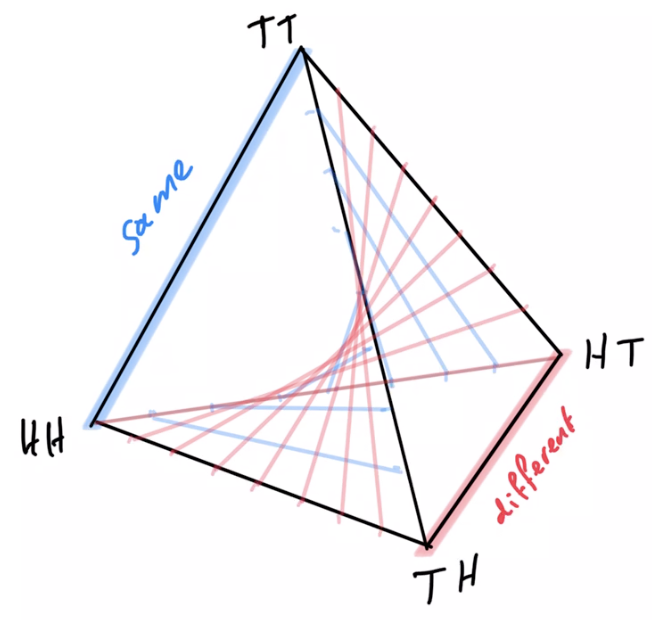
joint pdists \(p(a_1,a_2)\)
disjoint goal manifolds
agent manifold
\(p(a_1,a_2)=p(a_1)p(a_2)\)
Non-cooperative games
- In non-cooperative setting
- instead of maximizing goal probability:
- find Nash equilibria
- can we adapt PAI to do this?
- established that using EM algorithm alternatingly does not converge to Nash equilibria
- other adaptations may be possible...
- instead of maximizing goal probability:
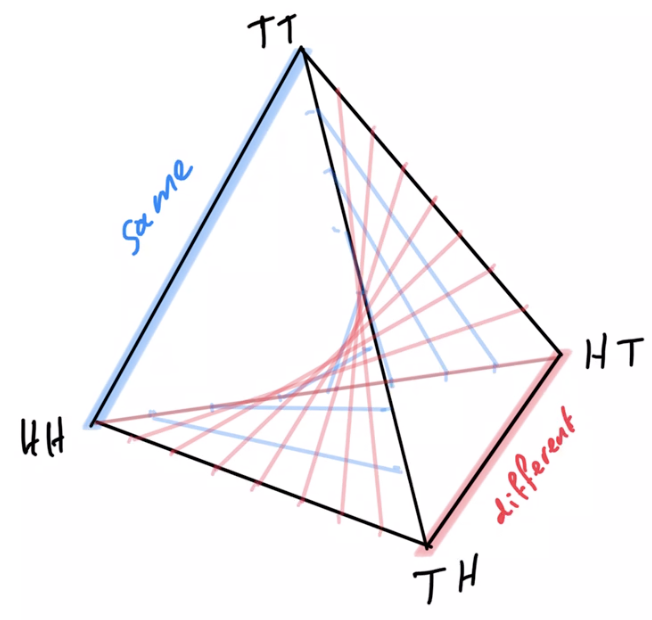
Non-cooperative games
- Counterexample for multi-agent alternating EM convergence:
- Two player game: matching pennies
- Each player \(P_i \in \{1,2\}\) controls a kernel \(p(a_i)\) determining probabilities of heads and tails
- First player wins if both pennies are equal second player wins if they are different
- Two player game: matching pennies

Non-cooperative games
- Counterexample for multi-agent alternating EM convergence:
- Nash equilibrium is known to be both players playing uniform distribution
- Using EM algorithm to fully optimize player kernels alternatingly does not converge
- Taking only single EM steps alternatingly also does not converge
EM
EM
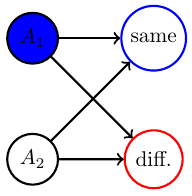

Non-cooperative games
- Counterexample for multi-agent alternating EM convergence
- fix a strategy for player 2 e.g. \(p_0(A_2=H)=0.2\)

Non-cooperative games
Text
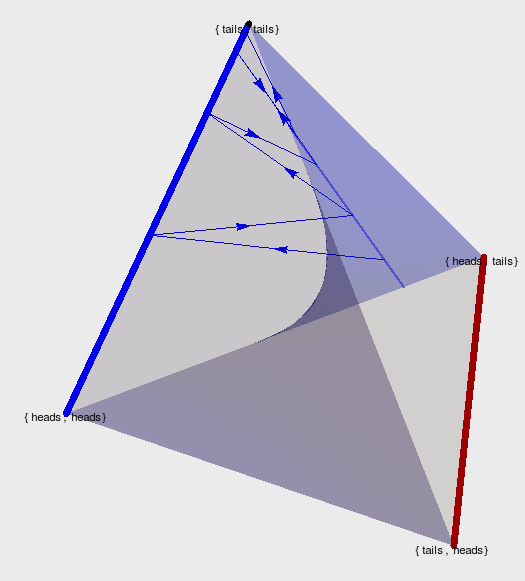
- run EM algorithm for P1
- Ends up on edge from (tails,tails) to (tails,heads)
- result: \(p(A_1=T)=1\)
- then optimizing P2 leads to \(p(A_2=H)=1\)
- then optimizing P1 leads to \(p(A_1=H)=1\)
- and on and on...
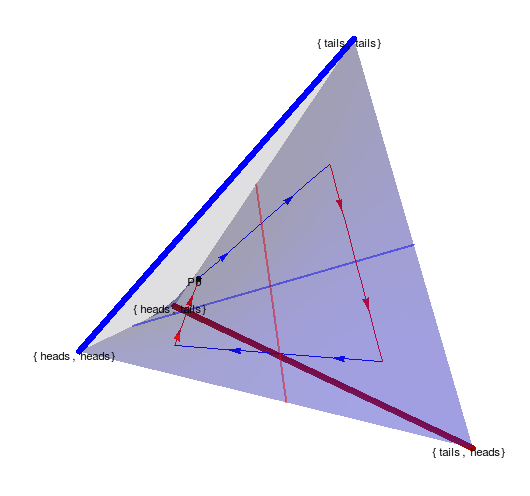
Non-cooperative games
Text
- Taking one EM step for P1 and then one for P2 and so on...
- ...also leads to loop.
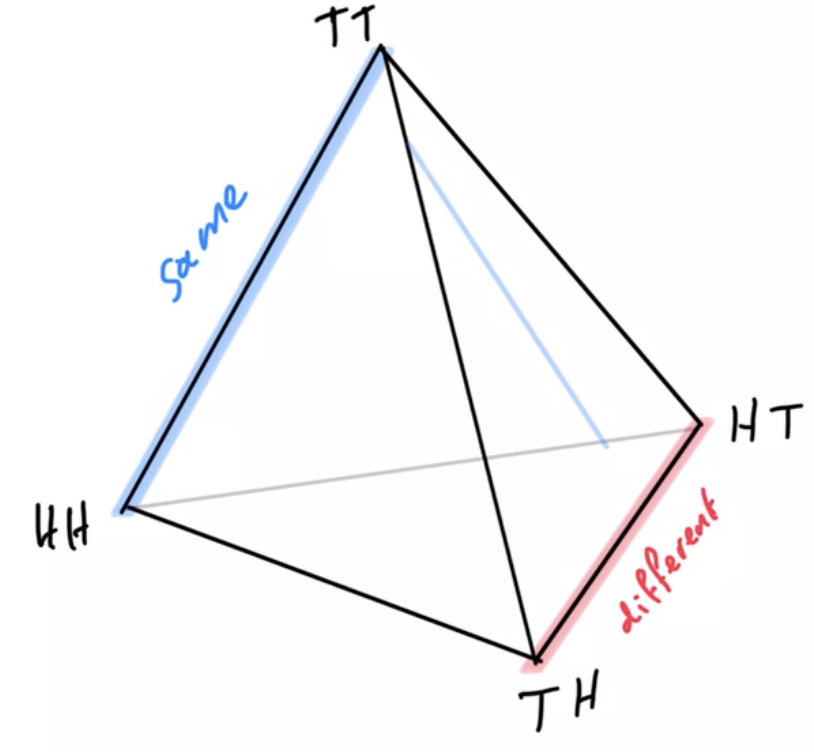
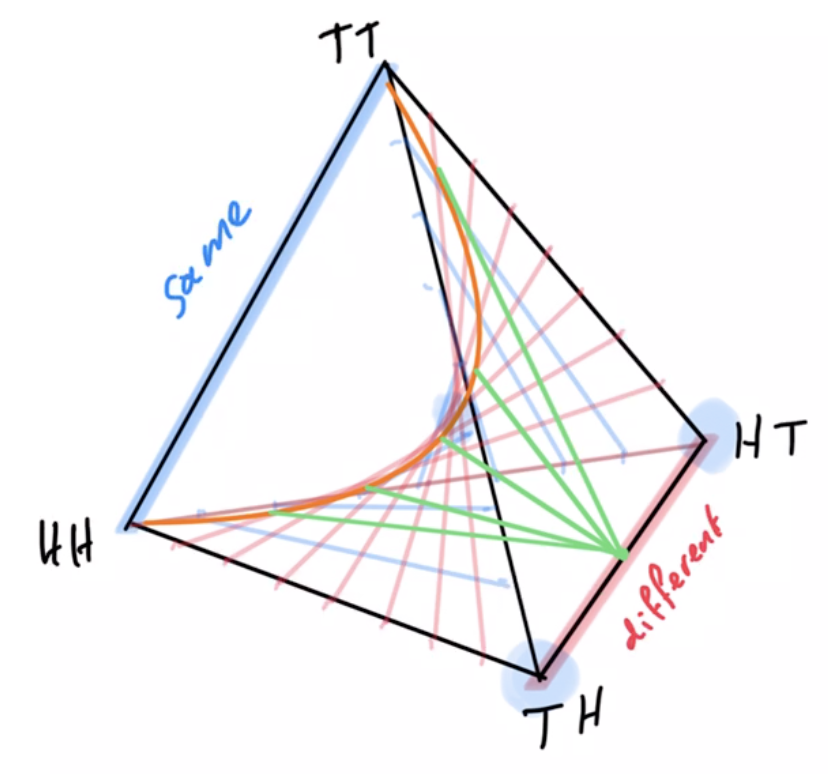
Cooperative games
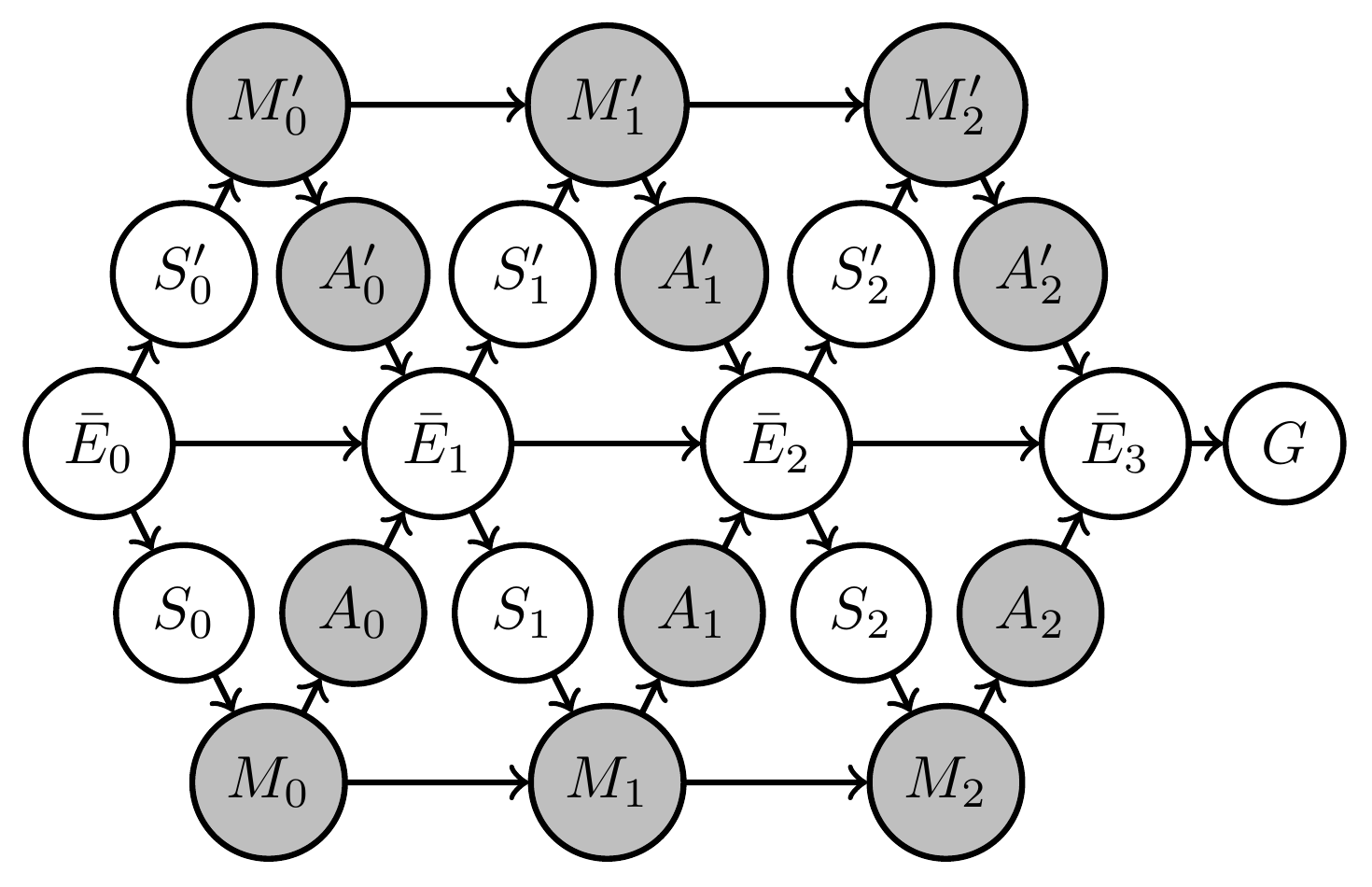
- Concrete example of agent manifold reduction under switch from single agent to multi-agent to identical multi-agent setup
- Like matching pennies but single goal: "different outcome"
- solution: one action/player always plays heads and one always tails
- agent manifold:
- single-agent manifold would be whole simplex
- multi-agent manifold is independence manifold
- multi-agent manifold with shared kernel is submanifold of independence manifold
- Like matching pennies but single goal: "different outcome"
Cooperative games





- Adding agents to system one of main goals
- Two kinds of scalability of agent number:
- Train \(n\) agents, run \(m\) agents
- agent number can change from \(n\) to \(m\) depending on events at runtime
Dynamic scalability of multi-agent systems
- Train \(n\) agents, use \(m\) agents
Dynamic scalability of multi-agent systems
Training \(n=1\) agents
Running \(m=2\) agents
2. Agent number can change from \(n\) to \(m\) depending on events at runtime
- Bayesian networks: network structure can't change due to events
- Need more general setting.
Dynamic scalability of multi-agent systems
Can't be combined in one Bayesian network!
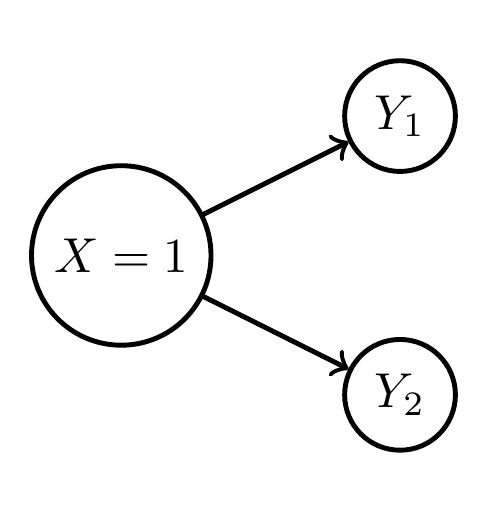
- E.g.: agent number can't depend on environment state:
Bayesian network limitations
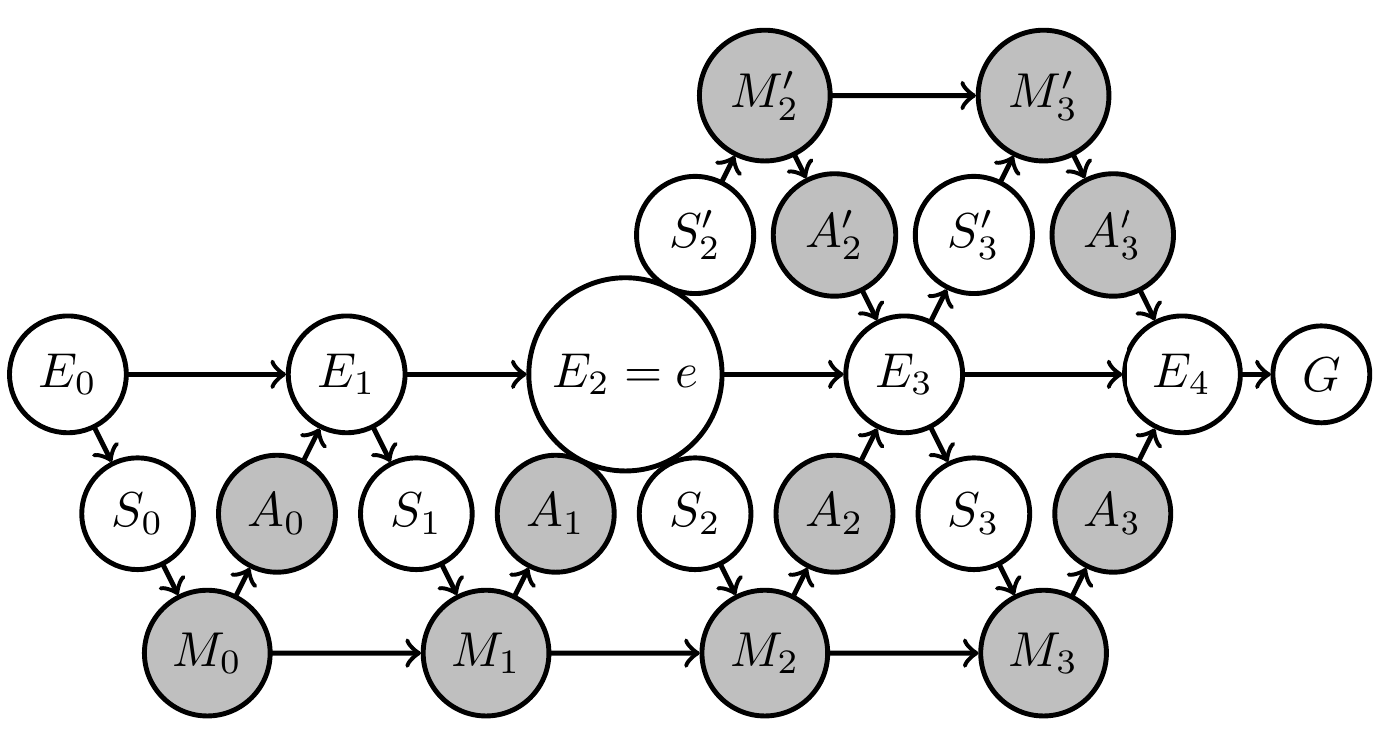
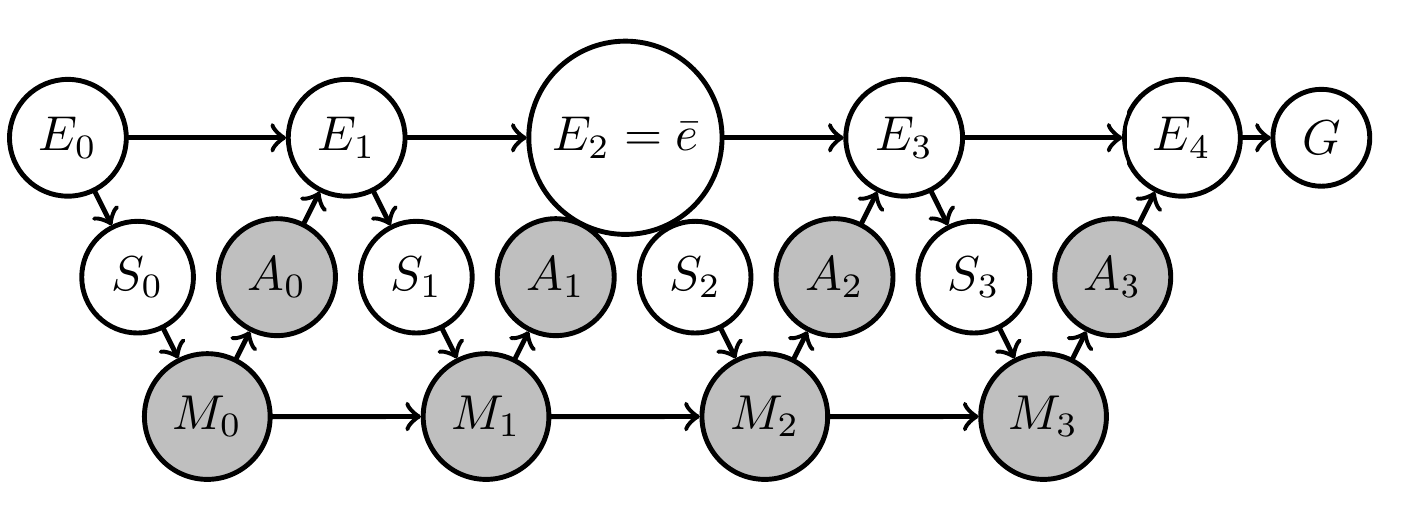
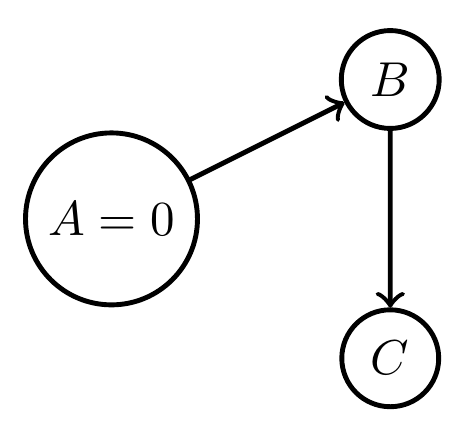
Can't be combined in one Bayesian network!
- E.g.: copy direction can't be changed
- if \(A=0\) let \(p(c|b)=\delta_b(c)\)
- if \(A=1\) let \(p(b|c)=\delta_c(b)\)
Can't be combined in one Bayesian network!
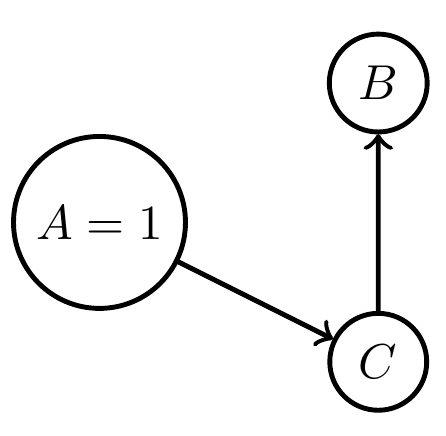
Bayesian network limitations
- Rollouts in Bayesian networks instantiate all variables
- Forks don't represent alternative consequences
- Forks represent multiple "parallel" consequences!
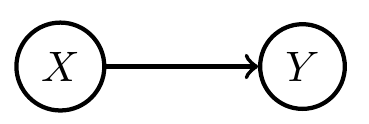
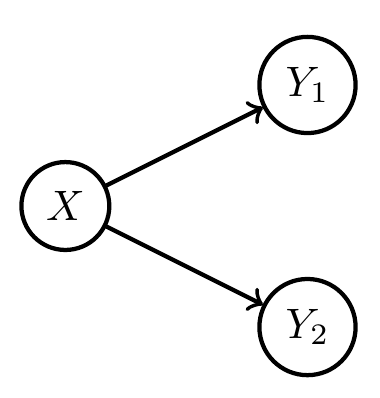
?
?
?


Bayesian network limitations

- Rollouts in Bayesian networks instantiate all variables
- Forks don't represent alternative consequences
- Forks represent multiple "parallel" consequences!
?


Bayesian network limitations


- Rollouts in Bayesian networks instantiate all variables
- Forks don't represent alternative consequences
- Forks represent multiple "parallel" consequences!


Bayesian network limitations
2. Agent number can change from \(n\) to \(m\) depending on events at runtime
- Solution: probabilistic programming replaces Bayesian networks
- e.g. change in copy direction now possible:
Dynamic scalability of multi-agent systems


Can be combined in this
probabilistic program!

2. Agent number can change from \(n\) to \(m\) depending on events at runtime
- Solution: probabilistic programming replaces Bayesian networks
- e.g. change in copy direction now possible
- trying scalability of agent number now straightforward!
- Promising way forward
- generalize planning as inference for probabilistic programs
- max likelihood already part of probabilistic programming language
- geometric picture unknown
- found others also consider: generalization of Bayesian networks are probabilistic programs \(\Rightarrow\) its probably correct!
- generalize planning as inference for probabilistic programs
Dynamic scalability of multi-agent systems
Coordination and communication from an information-theoretic perspective
- No progress yet
- Requires progress on other topics, like game theory
- May involve
- mechanism / game design i.e. non-fixed (sub-) goal nodes
- channel design i.e. non-fixed nodes in between agents
Bonus section: Planning as inference and Badger
Planning as inference and Badger
- Probably multiple ways possible
- Inner loop: Bayesian network / probabilistic program
- including multiple experts / agents (via possibly shared kernels)
- communication channels (via kernels)
- possibility to spawn new experts / change connectivity
- inner loop loss : generalization of goal node to multiple goal nodes (games)
- Outer loop: maximization of goal probability (e.g. em-algorithm)
Expected reward maximization
- PAI finds policy that maximizes probability of the goal event:
\[P^* = \text{arg} \max_{P \in M_A} p(G=1).\] - Often want to maximize expected reward of a policy:
\[P^* = \text{arg} \max_{P \in M_A} \mathbb{E}_P[r]\] - Can we solve the second problem via the first?
- Yes, at least if reward has a finite range \([r_{\text{min}},r_{\text{max}}]\):
- add binary goal node \(G\) to Bayesian network and set:
\[\newcommand{\ma}{{\text{max}}}\newcommand{\mi}{{\text{min}}}\newcommand{\bs}{\backslash}p(G=1|x):= \frac{r(x)-r_\mi}{r_\ma-r_\mi}.\]
- add binary goal node \(G\) to Bayesian network and set:

Expected reward maximization
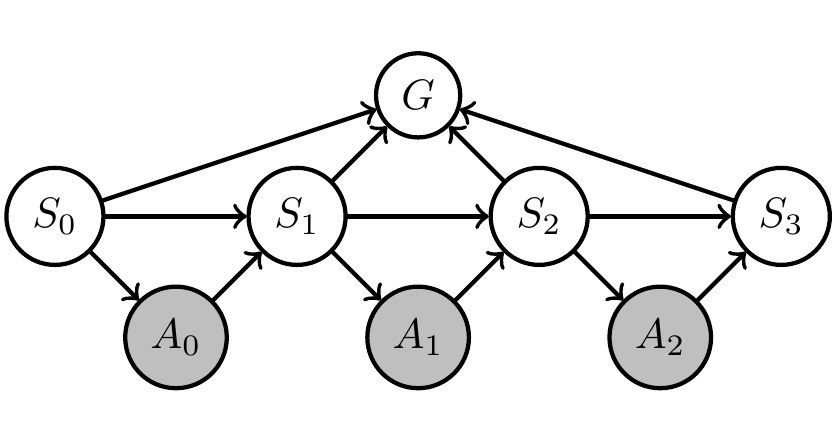
- Example application: Markov decision process
- reward only depending on states \(S_0,...,S_3\): \[r(x):=r(s_0,s_1,s_2,s_3)\]
- reward is sum over reward at each step:
\[r(s_0,s_1,s_2,s_3):= \sum_i r_i(s_i)\]

Expected reward maximization
- Relevance for project:
- reward based problems more common than goal event problems ((PO)MDPs, RL, losses...)
- extends applicability of framework
Parametrized kernels
- Often we don't want to choose the agent kernels completely freely e.g.:
- choose parametrized agent kernels
\[p(x_a|x_{\text{pa}(a)}) \to p(x_a|x_{\text{pa}(a)},\theta_a)\]
- choose parametrized agent kernels
- What do we have to adapt in this case?
- Step 3 of EM algorithm has to be adapted
Parametrized kernels
- Algorithm for parametrized kernels (not only conditioning and marginalizing anymore):
- Initial parameters \(\theta(0)\) define prior, \(P_0 \in M_A\).
- Get \(Q_t\), from \(P_t\) by conditioning on the goal: \[q_t(x) = p_t(x|G=1).\]
- Get \(P_{t+1}\), by replacing parameter \(\theta_a\) of each agent kernel with result of:
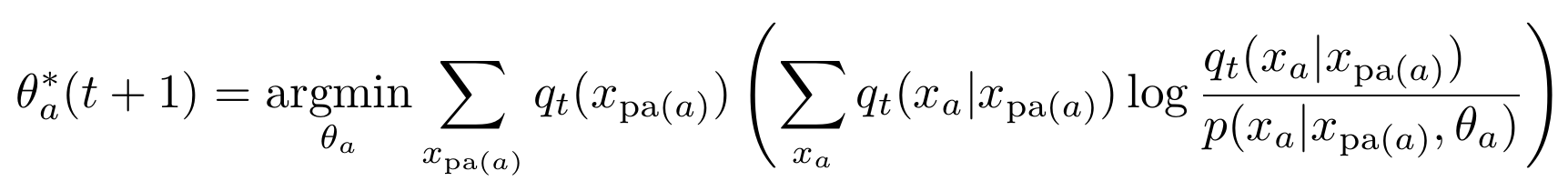
Parametrized kernels
- Relevance for project:
- needed for shared kernels
- needed for continuous random variables
- neural networks are parametrized kernels
- scalability
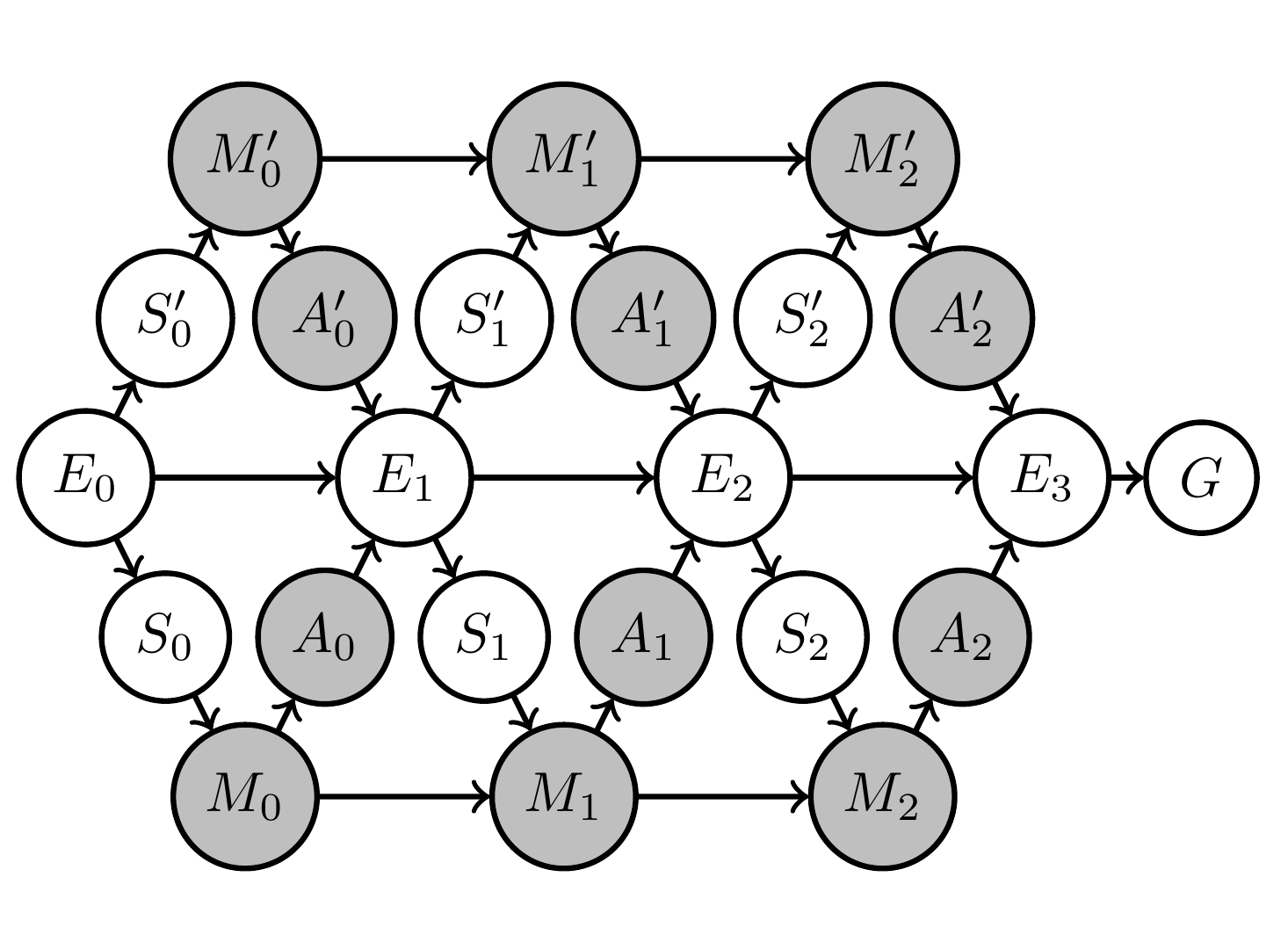
Shared kernels
- We also often want to impose the condition that multiple agent kernels are identical
- E.g. the three agent kernels in this MDP:

Shared kernels
- Introduce "types" for agent kernels
- let \(c(a)\) be the type of kernel \(a \in A\)
- kernels of same type share
- input spaces
- output space
- parameter
- then \(p_{c(a)}(x_a|x_{\text{pa}(a)},\theta_c)\) is the kernel of all nodes with \(c(a)=c\).
Shared kernels
- Example agent manifold change under shared kernels

Shared kernels
- Algorithm then becomes
- Initial parameters \(\theta(0)\) define prior, \(P_0 \in M_A\).
- Get \(Q_t\), from \(P_t\) by conditioning on the goal: \[q_t(x) = p_t(x|G=1).\]
- Get \(P_{t+1}\), by replacing parameter \(\theta_c\) of all agent kernels of type \(c\) with result of:
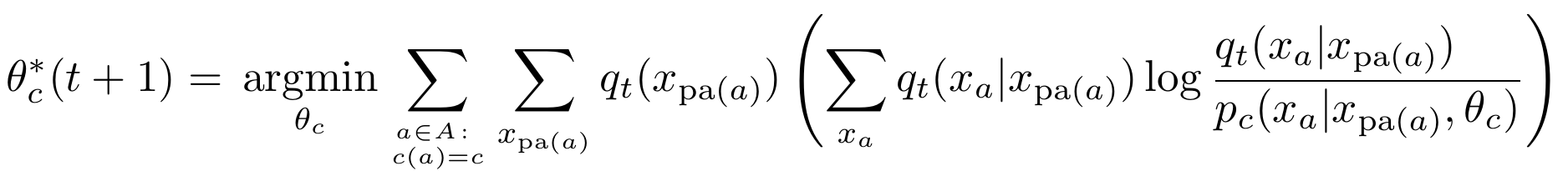
Shared kernels
- Relevance for project:
- scalability (less parameters to optimize)
- make it possible to have
- multiple agents with same policy
- constant policy over time
Multi-agents and games
- Relevance to project:
- dealing with multi-agent and multiple, possibly competing goals is a main goal of the project
- basis for studying communication and interaction
- basis for scaling up number of agents
- basis for understanding advantages of multi-agent setups
Uncertain (PO)MDP
- Assume
- (as usual) transition kernel of environment is constant over time, but
- we are uncertain about what is the transition kernel
- How can we reflect this in our setup / PAI?
- Can we find agent kernels that solve problem in a way that is robust against variation of those transition kernels?
Uncertain (PO)MDP
- Extend original (PO)MDP Bayesian network with two steps:
- parametrize environment transition kernels by shared parameter \(\phi\):
\[\bar{p}(x_e|x_{\text{pa}(e)}) \to \bar{p}_\phi(x_e|x_{\text{pa}(e)},\phi)\] - introduce prior distribution \(\bar{p}(\phi)\) over environment parameter
- parametrize environment transition kernels by shared parameter \(\phi\):
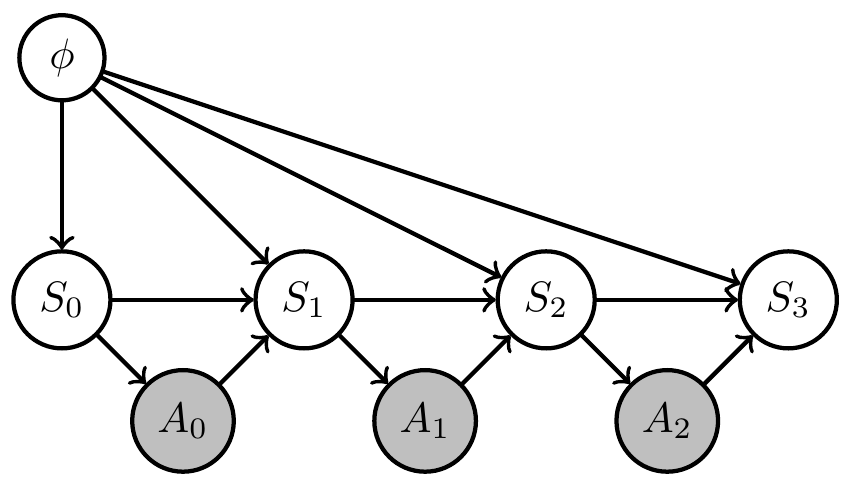
Uncertain (PO)MDP


- Same structure can be hidden in original network but in this way becomes a requirement/constraint
- If increasing goal probability involves actions that resolve uncertainty about the environment then PAI finds those actions!
- PAI results in curious agent kernels/policy.
Uncertain (PO)MDP
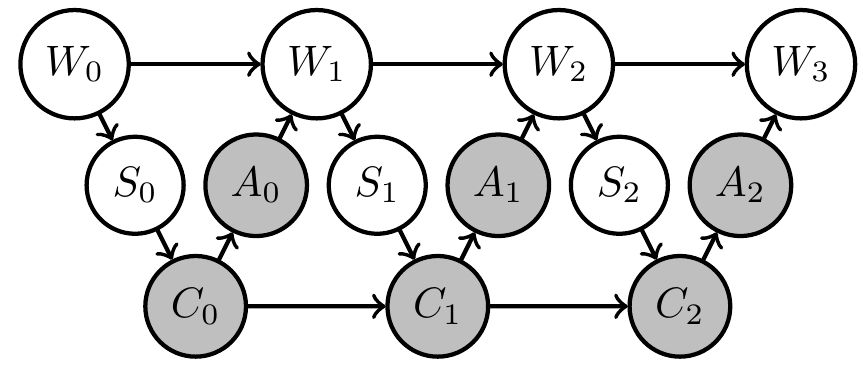
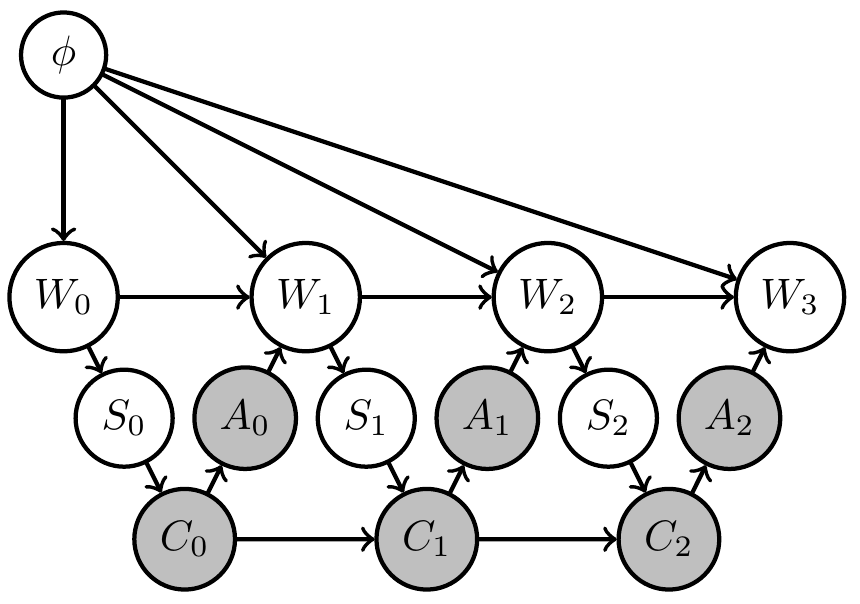
- Same structure can be hidden in original network but in this way becomes a requirement/constraint
- If increasing goal probability involves actions that resolve uncertainty about the environment then PAI finds those actions!
- PAI results in curious agent kernels/policy.
Uncertain (PO)MDP
-
Relevance for project:
- agents that can achieve goals in unknown / uncertain environments are important for AGI
- related to meta-learning
- understanding knowledge and uncertainty representation is important for agent design in general
Related project funded
- John Templeton Foundation has funded related project titled: Bayesian agents in a physical world
- Goal:
- What does it mean that a physical system (dynamical system) contains a (Bayesian) agent?
Related project funded
- Starting point:
- given system with inputs defined by
\[f:C \times S \to C\] - define a consistent Bayesian interpretation as:
- model / Markov kernel \(q: H \to PS\)
- interpretation function \(g:C \to PH\)
such that
\[g(c_{t+1})(h)=g(f(c_t,s_t))(h)=\frac{q(s_t|h) g(c_t)(h)}{\sum_{\bar h} q(s_t|\bar h) g(c_t)(\bar h)} \]
- given system with inputs defined by
Related project funded
- more suggestive notation:
\[g(h|c_{t+1})=g(h|f(c_t,s_t))=\frac{q(s_t|h) g(h|c_t)}{\sum_{\bar h} q(s_t|\bar h) g(\bar h|c_t)} \] - but note: \(PH_i\) are deterministic random variables and need no extra sample space
- \(H\) isn't even a deterministic random variable (what???)
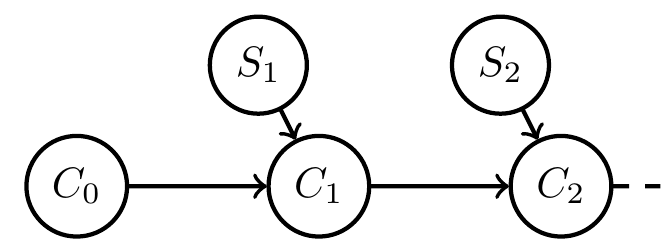
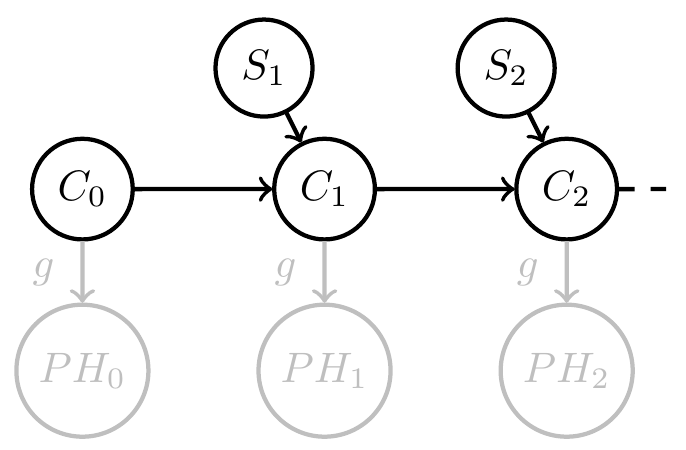
Related project funded
- Take away message :
- Formal condition for when a dynamical system with inputs can be interpreted as consistently updating probabilistic beliefs about the causes of its inputs (e.g. environment)
- Extensions to include stochastic systems, actions, goals, etc. ongoing...


Related project funded
- Relevance for project
- deeper understanding of relation between physical systems and agents will also help in thinking about more applied aspects
- a lot of physical agents are made of smaller agents and grow / change their composition, understanding this is also part of the funded project and is also directly relevant for the point "dynamical scalability of multi-agent systems" in the proposal
Two kinds of uncertainty
- Designer uncertainty:
- model our own uncertainty about environment when designing the agent to make it more robust / general
- Agent uncertainty:
- constructing an agent that uses specific probabilistic belief update method
- exact Bayesian belief updating (exponential families and conjugate priors)
- approximate belief updating (VAE world models?)
- constructing an agent that uses specific probabilistic belief update method
Two kinds of uncertainty
- Designer uncertainty:
- introduce hidden parameter \(\phi\) with prior \(\bar p(\phi)\) among fixed kernels
- planning as inference finds agent kernels / policy that deal with this uncertainty

Two kinds of uncertainty
- Agent uncertainty:
- In perception-action loop:
- construct agent's memory transition kernels that consistently update probabilistic beliefs about their environment
- these beliefs come with uncertainty
- can turn uncertainty reduction itself into a goal!
- In perception-action loop:
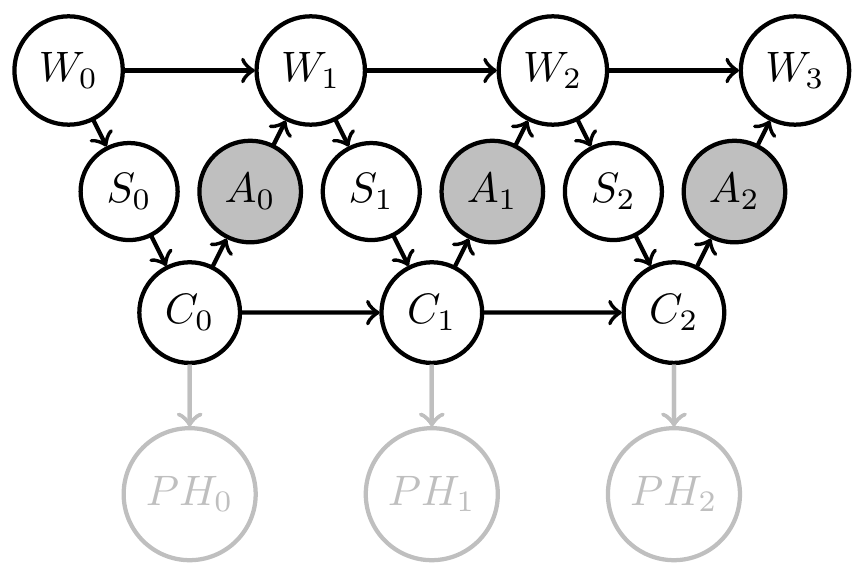
Two kinds of uncertainty

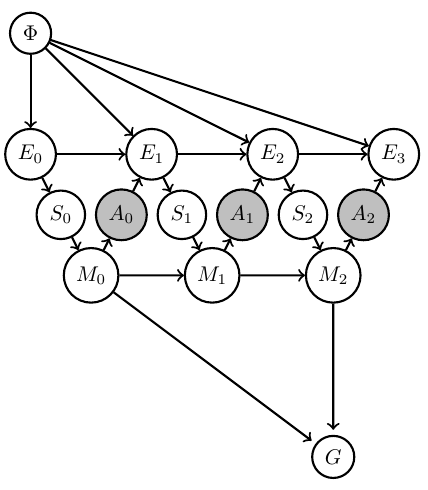
- Agent uncertainty:
- E.g: Define goal event via information gain :
\[G=1 \Leftrightarrow D_{KL}[PH_2(x)||PH_0(x)] > d\] - PAI solves for policy that employs agent memory to gain information / reduce its uncertainty by \(d\) bits
- E.g: Define goal event via information gain :
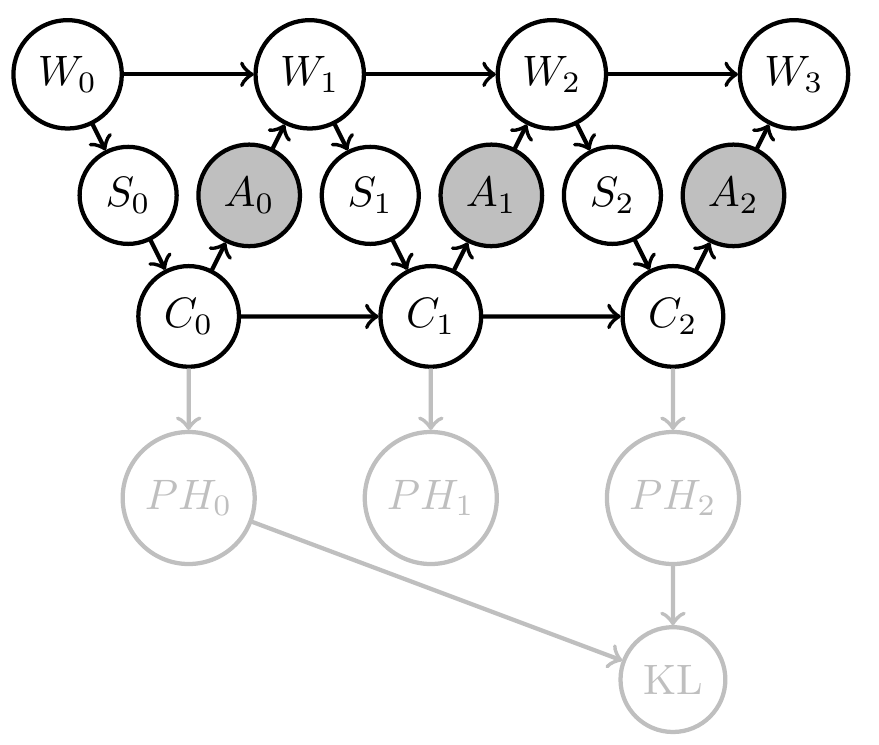
Two kinds of uncertainty
-
Relevance for project:
- taking decisions based on agent's knowledge is part of the project
Preliminary work
- Implementation of PAI in state of the art software (e.g. using Pyro)
- Planning to learn / uncertain MDP, bandit example.
- Do some agents have no interpretation e.g. the "Absent minded driver"? Collaboration with Simon McGregor.
- Design independence: some problems can be solved even if kernels are chosen independently others require coordinated choice of kernels, some are in between.
- Bayesian networks cannot change their structure dependent on the states of the contained random variables.
Preliminary work
- Implementation of PAI in state of the art software (e.g. using Pyro)
- Proofs of concept coded up in Pyro
- uses stochastic variational inference (SVI) for PAI instead of geometric EM
- may be useful to connect to work with neural networks since based on PyTorch
- For simple cases and visualizations also have Mathematica code
Preliminary work
2. Planning to learn / uncertain MDP, bandit example.
- currently investigating PAI for one armed bandit
- goal event is \(G=S_3=1\)
- actions choose one of two bandits that have different win probabilities determined by \(\phi\)
- agent kernels can use memory \(C_t\) to learn about \(\phi\)
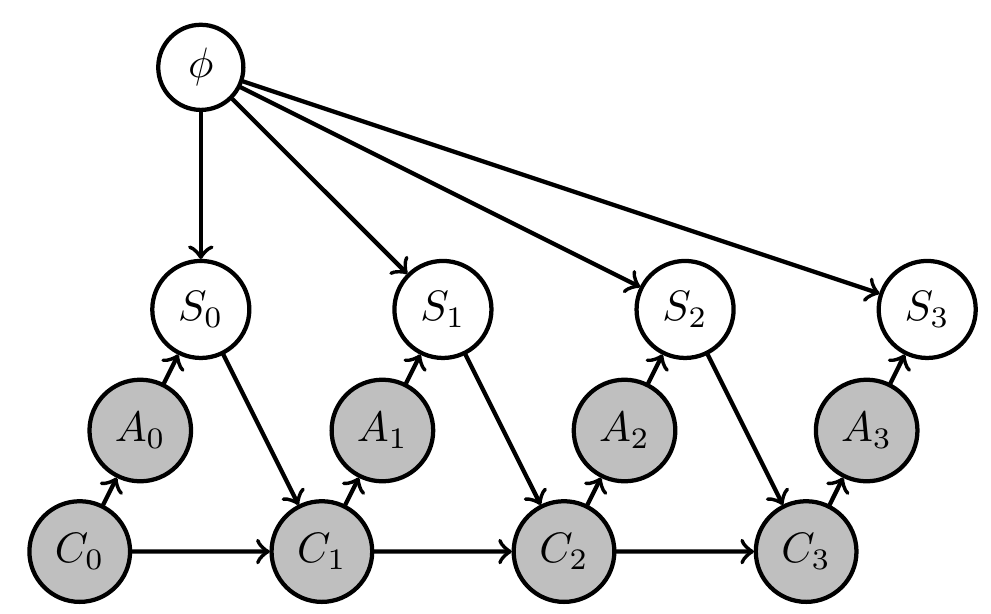
Preliminary work
- Do some agents have no interpretation e.g. the "Absent minded driver"? Collaboration with Simon McGregor.
- Driver has to take third exit
- all agent kernels share parameter \(\theta = \)probability of exiting
- optimal is \(\theta= 1/3\)
- Is this an agent even though it may have no consistent intepretation?
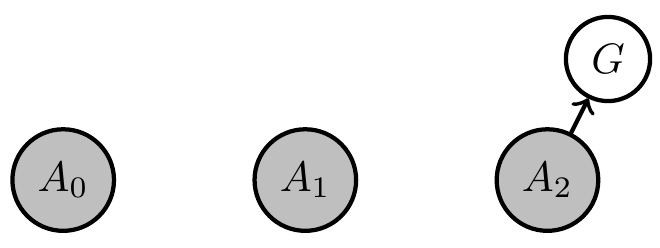
Preliminary work
- Design independence:
- some problems can be solved even if kernels are chosen independently
- others require coordinated choice of kernels,
- some are in between.
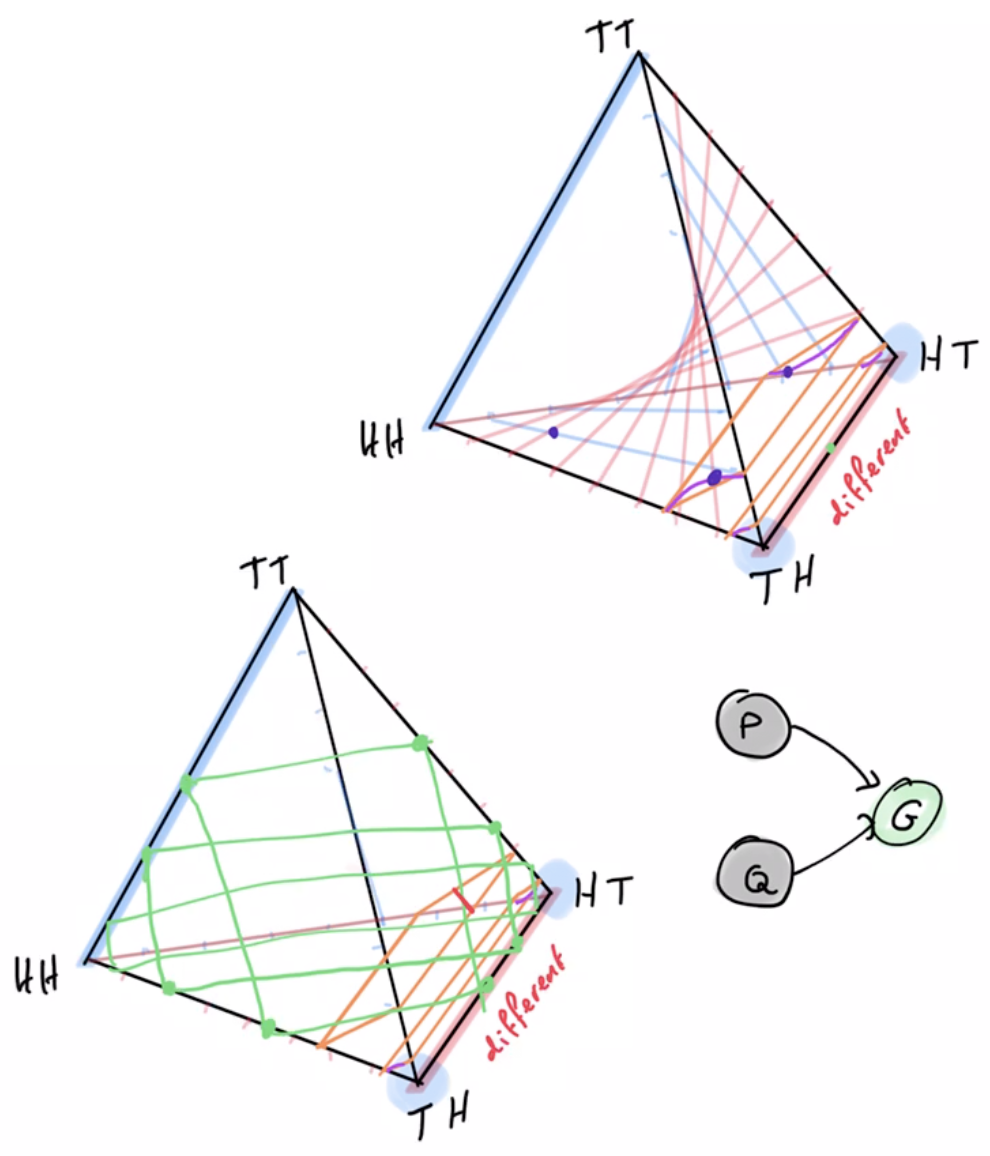
- Two player penny game
- goal is to get different outcomes
- one has to play heads with high probability the other has to play tails
- can't choose two kernels independently
Preliminary work
- Bayesian networks cannot change their structure dependent on the states of the contained random variables.
- Once we fix the (causal) Bayesian network it stays like that ...
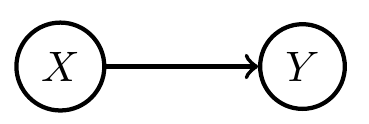

if x=1
Preliminary work
- Bayesian networks cannot change their structure dependent on the states of the contained random variables.
- Once we fix the (causal) Bayesian network it stays like that ...
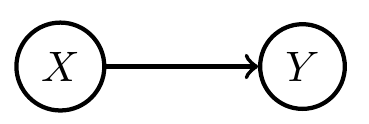

if x=1
But for adding and removing agents probably needed
Preliminary work
- Bayesian networks cannot change their structure dependent on the states of the contained random variables.
- Once we fix the (causal) Bayesian network it stays like that ...
- We are learning about modern ways to deal with such changes dynamically -- polynomial functors.
Thank you for your attention!
Uncertain MDP / RL
- In RL and RL for POMDPs the transition kernels of the environment are considered unknown / uncertain
Two kinds of uncertainty
- Saw before that we can derive policies that deal with uncertainty
- This uncertainty can be seen as the "designer's uncertainty"
- But we can also design agents that have models and come with their own well defined uncertainty
- For those we can turn uncertainty reduction itself into a goal!

Two kinds of uncertainty
- Agent uncertainty:
- e.g. for agent memory implement stochastic world model that updates in response to sensor values
- then by construction each internal state has a well defined associated belief distribution \(ph_t=f(c_t)\) over hidden variables
- turn uncertainty reduction itself into a goal!
- e.g. for agent memory implement stochastic world model that updates in response to sensor values