Exponential Distribution

Using the Exponential
Distribution to Find
Probabilities for Time
 

The mean, µ , of the Poisson distribution tells us how often we expect something of interest (an outcome) to happen within a certain period of time.

If the period of time you've chosen is, say, an hour, then

µt

is the number of times you expect an outcome to occur in t hours.
 

So if the Poisson formula,

\(prob(X) = \dfrac{e^{-\mu}\mu^X}{X!}\),

gives us the probability of an outcome occurring X times in an hour, then

\(prob(X) = \dfrac{e^{-\mu t}{\mu t}^X}{X!}\)

is the probability of it occurring X times in t hours.

\(prob(X) = \dfrac{e^{-\mu t}{\mu t}^X}{X!}\)

 

This modified Poisson formula now has an explicit time variable in it and, thus, gives us a better basis for turning the question around.

Instead of asking how often something will happen in a set period of time, we can now ask the time it takes for the outcome to happen (at least once).
 

How long it takes on average to get a single outcome is like asking the time span between outcomes, that is, the time where no outcomes occur at all.

If we want to know the probability of getting an outcome in t minutes, hours, days, etc., we simply ask our modified Poisson formula to give us the probability of getting X = 0 outcomes during the time interval t. It gives us:

 

\( prob(X) = \dfrac{e^{-\mu t}{\mu t}^0}{0!} = e^{-\mu t} \)

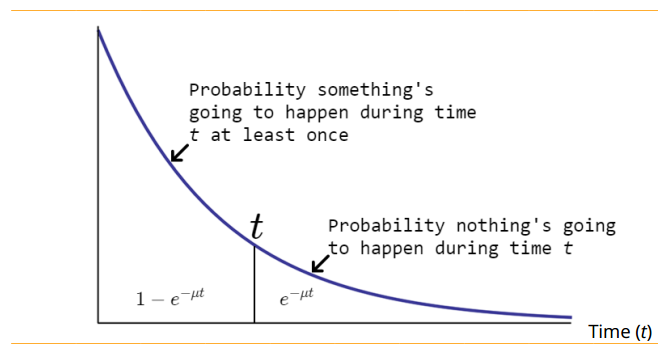
Here's what our new distribution looks like: