Chapter 29
\text{Chapter 29}
Chapter 29
\text{Chapter 29}
Chapter 29
\text{Chapter 29}
Chapter 29
\text{Chapter 29}
A current is set up in a wire loop that is formed as shown in FIGURE 10, where RI= 2.0 cm
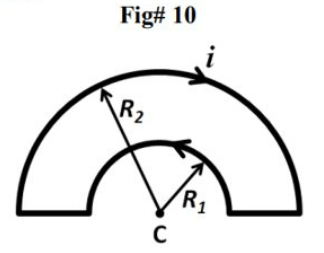
\text{A current is set up in a wire loop that is formed as shown in FIGURE 10, where $R_I=$ $2.0 \mathrm{~cm}$ }
and R2=4.0 cm. The loop carries a current of 5.0 A, as shown in the figure.
\text{and $R_2=4.0 \mathrm{~cm}$. The loop carries a current of $5.0 \mathrm{~A}$, as shown in the figure. }
What is the magnetic field at the center of the loop (C)?
\text{What is the magnetic field at the center of the loop (C)?}
A) 3.9×10−5 T out of the page
\text{
A) $3.9 \times 10^{-5} \mathrm{~T}$ out of the page
}
B) 3.9×10−5 T into the page
\text{
B) $3.9 \times 10^{-5} \mathrm{~T}$ into the page
}
C) 1.2×10−4 T out of the page
\text{
C) $1.2 \times 10^{-4} \mathrm{~T}$ out of the page
}
D) 1.2×10−4 T into the page
\text{
D) $1.2 \times 10^{-4} \mathrm{~T}$ into the page
}
E) 7.9×10−5 T into of the page
\text{
E) $7.9 \times 10^{-5} \mathrm{~T}$ into of the page
}
A current is set up in a wire loop that is formed as shown in FIGURE 10, where RI= 2.0 cm
\text{A current is set up in a wire loop that is formed as shown in FIGURE 10, where $R_I=$ $2.0 \mathrm{~cm}$ }
and R2=4.0 cm. The loop carries a current of 5.0 A, as shown in the figure.
\text{and $R_2=4.0 \mathrm{~cm}$. The loop carries a current of $5.0 \mathrm{~A}$, as shown in the figure. }
What is the magnetic field at the center of the loop (C)?
\text{What is the magnetic field at the center of the loop (C)?}
B1=4πR1μ0iϕ→ out of the page B2=4πR2μ0iϕ→ into the page B1>B2 because R2>R1∴Bc=B1−B2=4πμ0iϕ(R11−R21)=4π4π×10−7×5×π(21−41)×102=3.9×105 T→ out of the page
\begin{aligned}
& \mathrm{B}_1=\frac{\mu_0 i_\phi}{4 \pi \mathrm{R}_1} \rightarrow \text { out of the page } \\
& \mathrm{B}_2=\frac{\mu_0 i_\phi}{4 \pi \mathrm{R}_2} \rightarrow \text { into the page } \\
& \mathrm{B}_1>\mathrm{B}_2 \text { because } \mathrm{R}_2>\mathrm{R}_1 \\
& \therefore \mathrm{B}_{\mathrm{c}}=\mathrm{B}_1-\mathrm{B}_2=\frac{\mu_0 i_\phi}{4 \pi}\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right) \\
& =\frac{4 \pi \times 10^{-7} \times 5 \times \pi}{4 \pi}\left(\frac{1}{2}-\frac{1}{4}\right) \times 10^2=3.9 \times 10^5 \mathrm{~T} \rightarrow \text { out of the page }
\end{aligned}
In FIGURE 9, two infinitely long wires carry currents i. Each follows a 90∘ arc on the
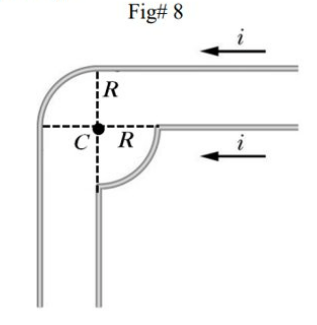
\text{In FIGURE 9, two infinitely long wires carry currents $\boldsymbol{i}$. Each follows a $90^{\circ}$ arc on the }
circumference of the same circle of radius R.
\text{circumference of the same circle of radius $\boldsymbol{R}$.}
What is the magnitude of the net magnetic field at the center of the circle (point C )?
\text{What is the magnitude of the net magnetic field at the center of the circle (point $\mathrm{C}$ )?}
A) 2πRμoi
\text{
A) $\frac{\mu_o i}{2 \pi R}$
}
B) πRμoi
\text{
B) $\frac{\mu_o i}{\pi R}$
}
C) 4πRμoi
\text{
C) $\frac{\mu_o i}{4 \pi R}$
}
D) 2πRμoi+16Rμoi
\text{
D) $\frac{\mu_o i}{2 \pi R}+\frac{\mu_o i}{16 R}$
}
E) πRμoi+16Rμoi
\text{
E) $\frac{\mu_o i}{\pi R}+\frac{\mu_o i}{16 R}$
}
In FIGURE 9, two infinitely long wires carry currents i. Each follows a 90∘ arc on the
\text{In FIGURE 9, two infinitely long wires carry currents $\boldsymbol{i}$. Each follows a $90^{\circ}$ arc on the }
circumference of the same circle of radius R.
\text{circumference of the same circle of radius $\boldsymbol{R}$.}
What is the magnitude of the net magnetic field at the center of the circle (point C )?
\text{What is the magnitude of the net magnetic field at the center of the circle (point $\mathrm{C}$ )?}
* The current in the straight inner wire does not produce any magnetic field
\text{
* The current in the straight inner wire does not produce any magnetic field
}
* The magnetic fields due to the circular sections cancel.
\text{
* The magnetic fields due to the circular sections cancel.
}
* We are left with the outer straight wires:
\text{
* We are left with the outer straight wires:
}
Bc=2× semi - infinite wires =2×4πRμ0i=2πRμ0i
\text{
$\mathrm{B}_{\mathrm{c}}=2 \times$ semi - infinite wires
$=2 \times \frac{\mu_0 \mathrm{i}}{4 \pi R}=\frac{\mu_0 \mathrm{i}}{2 \pi R}$
}
FIGURE 10 shows two long, thin wires, parallel to the z axis, carrying currents in the positive z
\text{FIGURE 10 shows two long, thin wires, parallel to the $z$ axis, carrying currents in the positive $z$ }
direction. The 50A wire is in the x−z plane and is 5 m from the z axis.
\text{direction. The $50\mathrm{A}$ wire is in the $x-z$ plane and is $5 \mathrm{~m}$ from the $z$ axis. }
The 40-A wire is in the y−z plane and is 4 m from the z axis.
\text{The 40-A wire is in the $y-z$ plane and is $4 \mathrm{~m}$ from the $z$ axis. }
What is the net magnetic field at the origin O due to the two wires?
\text{What is the net magnetic field at the origin $\mathrm{O}$ due to the two wires?}
A) (2i^−2j^)μT
\text{
A) $(2 \hat{i}-2 \hat{j}) \mu \mathrm{T}$
}
B) (2i^+2j^)μT
\text{
B) $(2 \hat{i}+2 \hat{j}) \mu T$
}
C) (2i^+3j^)μT
\text{
C) $(2 \hat{i}+3 \hat{j}) \mu T$
}
D) (2i^−3j^)μT
\text{
D) $(2 \hat{\mathbf{i}}-3 \hat{\mathbf{j}}) \mu \mathrm{T}$
}
E) (3i^+2j^)μT
\text{
E) $(3 \hat{i}+2 \hat{j}) \mu \mathrm{T}$
}
FIGURE 10 shows two long, thin wires, parallel to the z axis, carrying currents in the positive z
\text{FIGURE 10 shows two long, thin wires, parallel to the $z$ axis, carrying currents in the positive $z$ }
direction. The 50A wire is in the x−z plane and is 5 m from the z axis.
\text{direction. The $50\mathrm{A}$ wire is in the $x-z$ plane and is $5 \mathrm{~m}$ from the $z$ axis. }
The 40-A wire is in the y−z plane and is 4 m from the z axis.
\text{The 40-A wire is in the $y-z$ plane and is $4 \mathrm{~m}$ from the $z$ axis. }
What is the net magnetic field at the origin O due to the two wires?
\text{What is the net magnetic field at the origin $\mathrm{O}$ due to the two wires?}
B1=2πd1μ0i1(−j^)=2π×54π×10−7×50(−j^)=−2×10−6j^(T)=−2j^(μT)B2=+2πd2μ0i2i^=2π×44π×10−7×40(i^)=+2i^(μT)∴Bnet =(2i^−2j^)μT
\begin{aligned}
& \overrightarrow{\mathrm{B}}_1=\frac{\mu_0 \mathrm{i}_1}{2 \pi \mathrm{d}_1}(-\hat{\mathrm{j}}) \\
& =\frac{4 \pi \times 10^{-7} \times 50}{2 \pi \times 5}(-\hat{\mathrm{j}})=-2 \times 10^{-6} \hat{\mathrm{j}}(\mathrm{T})=-2 \hat{\mathrm{j}}(\mu \mathrm{T}) \\
& \overrightarrow{\mathrm{B}}_2=+\frac{\mu_0 \mathrm{i}_2}{2 \pi \mathrm{d}_2} \hat{\mathrm{i}} \\
& =\frac{4 \pi \times 10^{-7} \times 40}{2 \pi \times 4}(\hat{\mathrm{i}})=+2 \hat{\mathrm{i}}(\mu \mathrm{T}) \\
& \therefore \overrightarrow{\mathrm{B}}_{\text {net }}=(2 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}) \mu \mathrm{T}
\end{aligned}
Use the right hand rule for the direction of B
\text{Use the right hand rule for the direction of $\vec{B}$}
FIGURE 11 shows a cross section of three parallel wires each carrying a current of 5.0 A out of
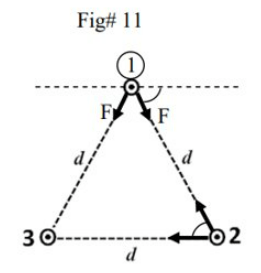
\text{FIGURE 11 shows a cross section of three parallel wires each carrying a current of $5.0 \mathrm{~A}$ out of }
the paper. If the distance d=6.0 mm, what is the magnitude of the net magnetic force on
\text{the paper. If the distance $\boldsymbol{d}=6.0 \mathrm{~mm}$, what is the magnitude of the net magnetic force on }
a 2.0m length of wire 1 ?
\text{a $2.0\mathrm{m}$ length of wire 1 ?}
A) 2.9mN
\text{
A) $2.9 \mathrm{mN}$
}
B) 3.3mN
\text{
B) $3.3 \mathrm{mN}$
}
C) 2.1mN
\text{
C) $2.1 \mathrm{mN}$
}
D) 3.9mN
\text{
D) $3.9 \mathrm{mN}$
}
E) 1.7mN
\text{
E) $1.7 \mathrm{mN}$
}
FIGURE 11 shows a cross section of three parallel wires each carrying a current of 5.0 A out of
\text{FIGURE 11 shows a cross section of three parallel wires each carrying a current of $5.0 \mathrm{~A}$ out of }
the paper. If the distance d=6.0 mm, what is the magnitude of the net magnetic force on
\text{the paper. If the distance $\boldsymbol{d}=6.0 \mathrm{~mm}$, what is the magnitude of the net magnetic force on }
a 2.0m length of wire 1 ?
\text{a $2.0\mathrm{m}$ length of wire 1 ?}
F=2πdμ0Li2=2π×6×10−34π×10−7×2×25=1.67×10−3 N Fnet =2. F ⋅sin60=2.9×10−3 N
\begin{aligned}
& \mathrm{F}=\frac{\mu_0 \mathrm{Li}^2}{2 \pi \mathrm{d}}=\frac{4 \pi \times 10^{-7} \times 2 \times 25}{2 \pi \times 6 \times 10^{-3}} \\
& =1.67 \times 10^{-3} \mathrm{~N} \\
& \mathrm{~F}_{\text {net }}=2 \text {. F } \cdot \sin 60=2.9 \times 10^{-3} \mathrm{~N} \\
&
\end{aligned}
A long, solid, cylindrical wire carries a uniformly distributed current. If the radius of the wire
\text{A long, solid, cylindrical wire carries a uniformly distributed current. If the radius of the wire}
is 3.5 mm, and the magnitude of the current density is 1.5 A/cm2, what is the magnitude of
\text{is $3.5 \mathrm{~mm}$, and the magnitude of the current density is $1.5 \mathrm{~A} / \mathrm{cm}^2$, what is the magnitude of}
the magnetic field at a distance of 2.5 mm from the axis of the wire?
\text{the magnetic field at a distance of $2.5 \mathrm{~mm}$ from the axis of the wire?}
A) 2.4×10−5 T
\text{
A) $2.4 \times 10^{-5} \mathrm{~T}$
}
B) 3.3×10−5 T
\text{
B) $3.3 \times 10^{-5} \mathrm{~T}$
}
C) 1.3×10−5 T
\text{
C) $1.3 \times 10^{-5} \mathrm{~T}$
}
D) 6.9×10−5 T
\text{
D) $6.9 \times 10^{-5} \mathrm{~T}$
}
E) zero
\text{
E) zero
}
A long, solid, cylindrical wire carries a uniformly distributed current. If the radius of the wire
\text{A long, solid, cylindrical wire carries a uniformly distributed current. If the radius of the wire}
is 3.5 mm, and the magnitude of the current density is 1.5 A/cm2, what is the magnitude of
\text{is $3.5 \mathrm{~mm}$, and the magnitude of the current density is $1.5 \mathrm{~A} / \mathrm{cm}^2$, what is the magnitude of}
the magnetic field at a distance of 2.5 mm from the axis of the wire?
\text{the magnetic field at a distance of $2.5 \mathrm{~mm}$ from the axis of the wire?}
∮B⋅ds==μ0ienc⇒B(2πr)=μ0.J⋅A=μ0 J.πr2B=2μ0Jr=24π×10−7×1.5×104×2.5×10−3=2.4×10−5 T
\begin{aligned}
& \oint \vec{B} \cdot d \vec{s}==\mu_0 i_{\mathrm{enc}} \Rightarrow B(2 \pi r)=\mu_0 . J \cdot A=\mu_0 \mathrm{~J} . \pi r^2 \\
& B=\frac{\mu_0 \mathrm{Jr}}{2}=\frac{4 \pi \times 10^{-7} \times 1.5 \times 10^4 \times 2.5 \times 10^{-3}}{2}=2.4 \times 10^{-5} \mathrm{~T}
\end{aligned}
C h a p t e r 2 9 \text{Chapter 29} C h a p t e r 2 9 \text{Chapter 29} C h a p t e r 2 9 \text{Chapter 29} C h a p t e r 2 9 \text{Chapter 29}