\text{Chapter III}

\text{Additional problem chapter II then Chapter 3 : Vectors}

\text{An object starts from rest at the origin and moves along the $x$ axis }

\text{with a constant acceleration of $4 \mathrm{~m} / \mathrm{s}^2$. Its average velocity as it goes }

\text{from $x=2 \mathrm{~m}$ to $x=18 \mathrm{~m}$ is:}

v_2^2=v_0^2+2a(x-x_0)\Rightarrow v_2^2=0+8(18-0)=144

v_2=12

v_1^2=v_0^2+2a(x-x_0)\Rightarrow v_1^2=0+8(2-0)=16

v_1=4

\displaystyle v_\text{avg}=\frac{x_2-x_1}{t_2-t_1}

\text{we need to find the times }t_1 \text{ and }t_2 \text{ using } v(t)=v_0+a t

\displaystyle v_\text{avg}=\frac{1}{2}(v(t)+v_0)=\frac{1}{2}(12+4)=8 \text{ m/s}

\displaystyle t1=\frac{v_1}{a}=\frac{4}{4}=1 s,t1=\frac{v_2}{a}=\frac{12}{4}=3s \Rightarrow v_{avg}=\frac{18-2}{3-1}=8 \text{ m/s}

\text{Method 2}

\text{An object starts from rest at the origin and moves along the $x$ axis }

\text{with a constant acceleration of $4 \mathrm{~m} / \mathrm{s}^2$. Its average velocity as it goes }

\text{from $x=2 \hspace{1mm}m$ to $x=18\hspace{1mm} m$ is:}

\text{A person walks from point A to B at a canstant speed of 18 km/h along straight line.}

\text{He then walks back to A at constant speed of 12 km/h. What is he avergae speed?}

\text{What is he avergae velocity?}

\text{A person walks from point A to B at a canstant speed of 18 km/h along straight line.}

\text{He then walks back to A at constant speed of 12 km/h. What is he avergae speed?}

\text{What is he avergae velocity?}

\displaystyle \text{The average speed is } S_\text{avg}=\frac{d_1+d_2}{t_2+t_1} \hspace{3 cm}(=\frac{\text{Total distance}}{\text{Total time}})

\displaystyle S_\text{avg}=\frac{d_1+d_2}{t_2+t_1}= \frac{d+d}{d/v_2+ d/v_1}=\frac{2 v_1 v_2}{v_1+v_2}=\frac{2\times18 \times12}{12+18}=14.4 \text{ km/h}

\displaystyle v_\text{avg}=\frac{x_f-x_i}{t_f-t_i}=0

\text{At a trafic light, a bike traveling at 2 m/s passes a car which is initially at rest. The bike }

\text{travels at a constant velocity. After 2s, the car starts moving and accelerates at 2.0 }m/s^2

A) 0.4 s

B) 1.5s

C) 2.4s

D) 3.2s

E) 5.2 s

\text{How much time does the car take to catch up with the bike}

A) 0.4 s

B) 1.5s

C) 2.4s

D) 3.2s

E) 5.2 s

\text{After 2s, the bike is at the position }x=2\times 2=4m

\text{Therefore, its position as a given time is } x_1(t)=x_0+v t=4+2t

\text{The car's position is }x_2-x_0=vt+\frac{1}{2} a t^2\Rightarrow x_2(t)=t^2

\text{The two mobiles will meet when }x_1=x_2\Rightarrow t^2=4+2t

\text{The solution to this equation of second order is } t=1+\sqrt{5}\approx3.2s

\text{At a trafic light, a bike traveling at 2 m/s passes a car which is initially at rest. The bike }

\text{travels at a constant velocity. After 2 s, the car starts moving and accelerates at 2.0 } \mathrm{~m/s^2}

\text{How much time does the car take to catch up with the bike}

A) 0.4 s

B) 1.5s

C) 1.7s

D) 3.5s

E) 5.2 s

\text{What is the time difference between the two meetings?}

\text{At a trafic light, a car starts moving and accelerates at 2.0 } \mathrm{~m/s^2}

\text{At that moment, a bike, 6 m behind the car, was moving at a constant velocity of }6 \mathrm{~m/s}.

\text{The two mobiles will meet twice.}

\text{What is the time difference between the two meetings?}

A) 0.4 s

B) 1.5s

C) 1.7s

D) 3.5s

E) 5.2 s

\text{At the starting time, the bike is at the position }x_0=-6m

\text{Therefore, its position at a given time is } x_1(t)=x_0+v t=-6+6t

\text{The car's position is }x_2-x_0=vt+\frac{1}{2} a t^2\Rightarrow x_2(t)=t^2

\text{The two mobiles will meet when }x_1=x_2\Rightarrow t^2=-6+6t

\text{The solution to this equation of second order are } t={3\pm\sqrt{3}}

\text{What is the time difference between the two meetings?}

\Delta t=t_2-t_1=2\sqrt{3}\approx3.46 \mathrm{~s}

\text{At a trafic light, a car starts moving and accelerates at 2.0 } \mathrm{~m/s^2}

\text{At that moment, a bike, 6 m behind the car, was moving at a constant velocity of }6 \mathrm{~m/s}.

\text{The two mobiles will meet twice.}

\text{What is the time difference between the two meetings?}

\text{the velocity of the particle as function of time is show in Fig 1.}

A) 0.4 \text{ m/s}

B) 1.2 \text{ m/s}

C) 1.4 \text{ m/s}

D) 3.6 \text{ m/s}

E) 5.2 \text{ m/s}

\text{The average velocity of the particle between $\mathrm{t}=0.0 \mathrm{~s}$ and $5.0 \mathrm{~s}$ is:}

\text{A particle starts from the origin at $t=0$ and moves along the positive $x$-axis. A graph of }

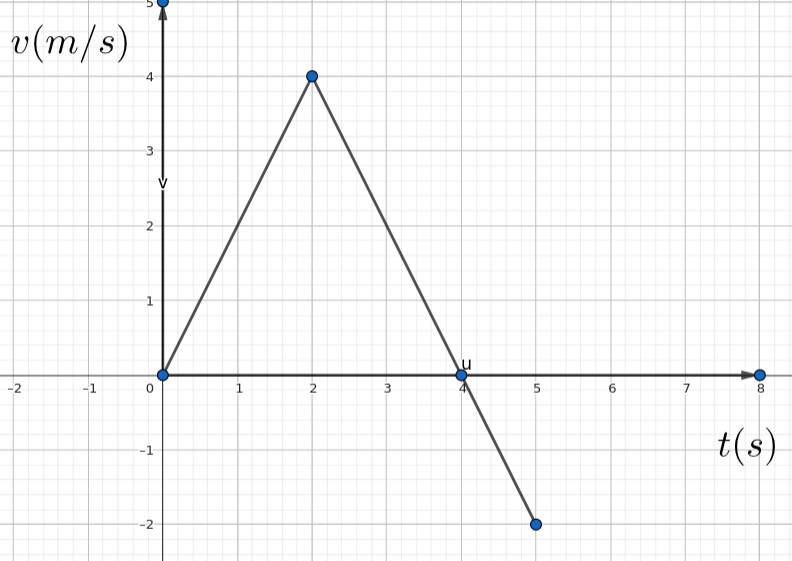
A) 0.4 \text{ m/s}

B) 1.2 \text{ m/s}

C) 1.4 \text{ m/s}

D) 3.6 \text{ m/s}

E) 5.2 \text{ m/s}

\displaystyle v_\text{avg}=\frac{x_f-x_i}{t_f-t_i}=\frac{\text{Area}}{t_f-t_i}

\displaystyle \text{Area}=\frac{1}{2}(4\times 4)\textcolor{red}{-}\frac{1}{2}(1\times 2)=7

v_\text{avg}=7/5=1.4\text{ m/s}

\text{the velocity of the particle as function of time is show in Fig 1.}

\text{The average velocity of the particle between $\mathrm{t}=0.0 \mathrm{~s}$ and $5.0 \mathrm{~s}$ is:}

\text{A particle starts from the origin at $t=0$ and moves along the positive $x$-axis. A graph of }

A) 29 \text{ m/s}

B) 12 \text{ m/s}

C) 17 \text{ m/s}

D) 33 \text{ m/s}

E) 35 \text{ m/s}

\text{An object is thrown vertically upward. It has an upward velocity of $25 \mathrm{~m} / \mathrm{s}$ when it reaches }

\text{one fourth of its maximum height above its launch point. }

\text{What is initial launch speed of the object? (Ignore the air resistance)}

A) 29 \text{ m/s}

B) 12 \text{ m/s}

C) 17 \text{ m/s}

D) 33 \text{ m/s}

E) 35 \text{ m/s}

\text{Maximum height is: }\displaystyle h=\frac{v_0^2}{2g}

\text{ (Formula sheet)}

\displaystyle v^2=v_0^2-2 g \underbrace{\left(x-x_0\right)}_{\displaystyle \frac{h}{4}}

\displaystyle =v_0^2-2 g \times \frac{v_0^2}{2 g} \times \frac{1}{4}=\frac{3}{4}v_0^2

\displaystyle v_0=\frac{2}{\sqrt{3}} v

\displaystyle v_0=\frac{2}{\sqrt{3}} 25 \simeq 29 \mathrm{~m} / \mathrm{s}

\text{An object is thrown vertically upward. It has an upward velocity of $25 \mathrm{~m} / \mathrm{s}$ when it reaches }

\text{one fourth of its maximum height above its launch point. }

\text{What is initial launch speed of the object? (Ignore the air resistance)}

\text{Two runners Roger and Abbot are running on a straight track along $x$ axis from $t=0$ to $t=t_f$. }

\text{Abbot runs throughout the interval $t=0$ to $t=t_f$ at a constant speed $v_{\mathrm{Abbot}}$, while Roger }

\text{has a velocity that depends upon time as shown in Figure $2\left(t_{\max } \neq t_f / 2\right)$. Both the runners }

\text{ travelled the same displacement during the time interval. }

{\text{A) $v_{A b b o t}=v_{\max } /2$}}\\ \text{B) $v_{\text {Abbot }}=v_{\text {max }}$}\\ \text{C) $v_{A b b o t}=2 v_{\max }$}\\ \text{ \hspace{.3cm} D) $v_{\text {Abbot }}=3 v_{\max } / 2$}\\ \text{E) $v_{A b b o t}=v_{\max } / 3$}\\

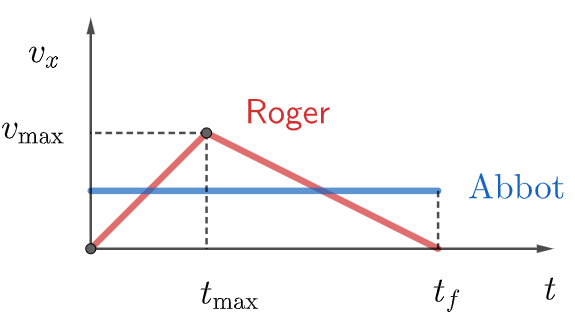
\text{What is the relation between $v_{\mathrm{Abbot}}$ and $v_{\max }$.}

\underline{\text{A) $v_{A b b o t}=v_{\max } /2$}}\\ \text{B) $v_{\text {Abbot }}=v_{\text {max }}$}\\ \text{C) $v_{A b b o t}=2 v_{\max }$}\\ \text{ \hspace{.3cm} D) $v_{\text {Abbot }}=3 v_{\max } / 2$}\\ \text{E) $v_{A b b o t}=v_{\max } / 3$}\\

\Delta X_{\text {Roger }}=\frac{1}{2} t_f V_{\max }

\Delta X_{\text {Roger }}=t_f \times V_{\text {Abbot }}

t_f \cdot V_{\text {Abbot }}=\frac{1}{2} V_{\max } \cdot t_f

\displaystyle V_{\text {Abbot }}=\frac{V_{\max }}{2}

\text{(Area under the red curve)}

\text{(Area under the blue curve)}

\text{(Travelled the same displacement)}

\text{Two runners Roger and Abbot are running on a straight track along $x$ axis from $t=0$ to $t=t_f$. }

\text{Abbot runs throughout the interval $t=0$ to $t=t_f$ at a constant speed $v_{\mathrm{Abbot}}$, while Roger }

\text{has a velocity that depends upon time as shown in Figure $2\left(t_{\max } \neq t_f / 2\right)$. Both the runners }

\text{Vectors}

A) 2.0 \hat{i}-3.0 \hat{k}

B) 4.0 \hat{i}-2.0 \hat{k}

C) -12 \hat{i}

D)\hat{j}+\hat{k}

E) -8.0 \hat{j}

\text { Let } \vec{A}=2.0 \hat{i}-3.0 \hat{k} \text { and } \vec{B}=2.0 \hat{i}+\hat{k} \text {. The vector } \vec{D}=(\vec{A}-\vec{B}) \times \vec{A} \text { is: }

A) 2.0 \hat{i}-3.0 \hat{k}

B) 4.0 \hat{i}-2.0 \hat{k}

C) -12 \hat{i}

D)\hat{j}+\hat{k}

E) -8.0 \hat{j}

\vec{A}-\vec{B}=-4\vec{k}

D=(\vec{A}-\vec{B})\times \vec{A}=-4\vec{k}\times(2\hat{i}-3\hat{k})=-8\hat{j}

\text{because }\hat{k}\times\hat{k}=0 \text{and }\hat{k}\times\hat{i}=\hat{j}

\text { Let } \vec{A}=2.0 \hat{i}-3.0 \hat{k} \text { and } \vec{B}=2.0 \hat{i}+\hat{k} \text {. The vector } \vec{D}=(\vec{A}-\vec{B}) \times \vec{A} \text { is: }

A)-3.33

B) +3.33

C) -0.400

D)+0.400

E) -0.300

\text{Two vectors are given by $\vec{A}=2.00 \hat{\imath}+2.00 \hat{\jmath}-$ $1.00 \hat{k}$ and $\vec{B}=7.00 \hat{\imath}+24 \hat{k}$. }

\text{What is the component of $\vec{B}$ along the direction of $\vec{A}$ ?}

\text{(Major1 term 221)}

A)-3.33

B) +3.33

C) -0.400

D)+0.400

E) -0.300

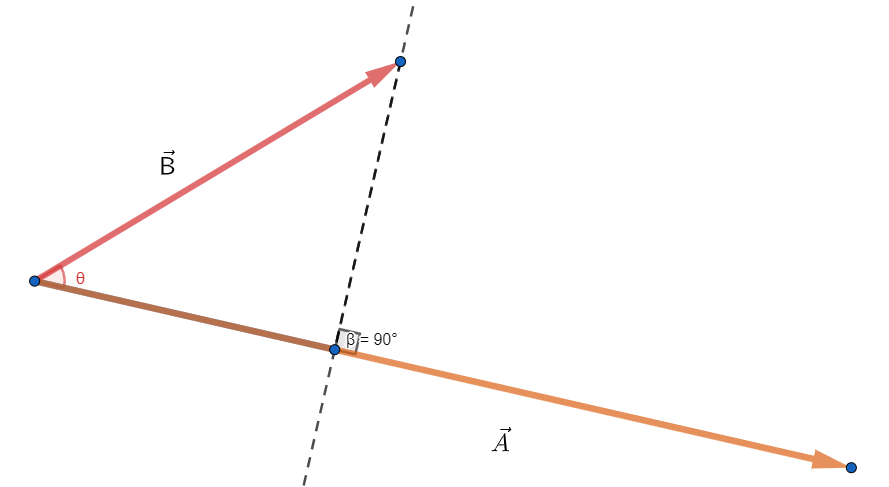
\text{It is the projection of }\vec{B} \text{ over the vector }\vec{A}

\vec{A}. \vec{B}= A B \cos{\theta}

\displaystyle \Rightarrow B\cos{\theta}=\frac{\vec{A}.\vec{B}}{A}=\frac{A_x B_x+A_y B_y+A_z B_z}{A}=-3.33

\displaystyle A=\sqrt{2^2+2^2+1^2}=3

\text{general concept}

\text{Two vectors are given by $\vec{A}=2.00 \hat{\imath}+2.00 \hat{\jmath}-$ $1.00 \hat{k}$ and $\vec{B}=7.00 \hat{\imath}+24 \hat{k}$. }

\text{What is the component of $\vec{B}$ along the direction of $\vec{A}$ ?}

\text{(Major1 term 221)}

A) 7.4

B) 5.3

C) 8.6

D)4.6

E) 6.3

\text{(Major1 term 221)}

\text{If vector $\vec{P}$ is added to vector $\vec{Q}=2.0 \hat{\imath}+6.0 \hat{\jmath}$, the result is a vector pointing in }

\text{the positive direction of the x-axis, with a magnitude equal to that of $\vec{Q}$.}

\text{What is the magnitude of $\vec{P}$ ?}

A) 7.4

B) 5.3

C) 8.6

D)4.6

E) 6.3

\text{The resultant is along x-axis so: } \vec{C}=a \hat{i}

\text{its magnitude is the same as that of }\vec{Q}, \text{ i.e. } Q=\sqrt{2^2+6^2}=\sqrt{40}

\text{we deduce that }\vec{C}=\sqrt{40} \hat{i}

\vec{P}+\vec{Q}=\vec{C}\Rightarrow \vec{P}=\vec{C}-\vec{Q}=(\sqrt{40}-2)\hat{i}-6\hat{j}

\displaystyle P=\sqrt{(\sqrt{40}-2)^2+6^2}=7.4

\text{Let us put } \vec{P}+\vec{Q}=\vec{C}

\text{(Major1 term 221)}

\text{If vector $\vec{P}$ is added to vector $\vec{Q}=2.0 \hat{\imath}+6.0 \hat{\jmath}$, the result is a vector pointing in }

\text{the positive direction of the x-axis, with a magnitude equal to that of $\vec{Q}$.}

\text{What is the magnitude of $\vec{P}$ ?}

A) 3

B) 4

C) 2

D)1

E) -3

\text{(Major1 term 221)}

\text{Two vectors are represented by $\vec{A}=c \hat{\imath}+2.0 \hat{\jmath}+8.0 \hat{k}$ and $\vec{B}=2.0 \hat{\imath}+\hat{\jmath}+4.0 \hat{k}$.}

\text{ For what values of $c$ will these vectors be parallel to each other?}

A) 3

B) 4

C) 2

D)1

E) -3

\text{ Method I (lengthy)}

\vec{A}\parallel \vec{B}\Rightarrow \vec{A}\times\vec{B}=0

\vec{A}\times\vec{B}=(2 \times4-8\times1)\hat{i}+(8\times2-4\times c)\hat{j}+(c\times1-2\times2)\hat{k}

\text{from both equations, we need:}

16-4c=0

c-4=0

\text{and }

c=4

\text{(Major1 term 221)}

\text{Two vectors are represented by $\vec{A}=c \hat{\imath}+2.0 \hat{\jmath}+8.0 \hat{k}$ and $\vec{B}=2.0 \hat{\imath}+\hat{\jmath}+4.0 \hat{k}$.}

\text{ For what values of $c$ will these vectors be parallel to each other?}

A) 3

B) 4

C) 2

D)1

E) -3

\text{ Method II}

\text{The vectors are parallel} \Rightarrow

{\text{the ratio of the components is the same}}

\displaystyle \frac{c}{2}=\frac{2}{1}=\frac{8}{4}\Rightarrow

c=4

\text{(Major1 term 221)}

\text{Two vectors are represented by $\vec{A}=c \hat{\imath}+2.0 \hat{\jmath}+8.0 \hat{k}$ and $\vec{B}=2.0 \hat{\imath}+\hat{\jmath}+4.0 \hat{k}$.}

\text{ For what values of $c$ will these vectors be parallel to each other?}

A) 3.07

B) 2.71

C) 2.24

D)1.23

E) 1.55

\text{$\vec{P}$ and $\vec{Q}$ are two vectors with the same magnitude and angle $\theta=30^\circ$ between them. }

\text{If their sum is $\vec{P}+\vec{Q}=-3\hat{i}$, what is their magnitude?}

A) 3.07

B) 2.71

C) 2.24

D)1.23

E) 1.55

\displaystyle \text{$(\vec{P}+\vec{Q})^2=(-3\hat{i})^2 \Rightarrow P^2+2\vec{P}.\vec{Q}+Q^2=9 $}

\displaystyle \text{$\Rightarrow P^2+2 P Q \cos(30^\degree)+Q^2=9 $}

\text{$\displaystyle \Rightarrow2 P^2+2 P^2 \frac{\sqrt{3}}{2}=9 $}

\text{$\displaystyle \Rightarrow P^2(1+ \frac{\sqrt{3}}{2})=\frac{9}{2} $}

\text{$\displaystyle \Rightarrow P^2=\frac{9}{2+\sqrt{3}} $}

\text{$\displaystyle \Rightarrow P=\frac{3}{\sqrt{2+\sqrt{3}} }=1.55$}

(\text{because $P=Q$})

\text{ Method I}

\text{$\vec{P}$ and $\vec{Q}$ are two vectors with the same magnitude and angle $\theta=30^\circ$ between them. }

\text{If their sum is $\vec{P}+\vec{Q}=-3\hat{i}$, what is their magnitude?}

\text{The square of a vector is the magnitude square.}

\text{ Method II}

\text{If the sum of two vectors is along x, they should be symmetric on the x-Axis}

\text{in other words, they will have \textcolor{green}{opposit y-components } and the same x-components}

\text{$\vec{P}=a\hat{i}+b\hat{j}$}

\text{$\vec{Q}=a\hat{i}-b\hat{j}$}

\text{$\vec{P}+\vec{Q}=-3\hat{i} \Rightarrow 2a\hat{i}=-3\hat{i}\Rightarrow a=-3/2$}

\text{$a=P \cos(180-30^\degree/2)\Rightarrow P=a/\cos(165^\degree)$}

\text{$\Rightarrow P=1.55$}

(\text{If the angle btween them is $30^\degree$, then the angle between them and the x-axis is $180^\degree-15^\degree$})

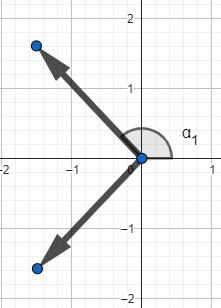
\text{$\vec{P}$ and $\vec{Q}$ are two vectors with the same magnitude and angle $\theta=30^\degree$ between them. }

\text{If their sum is $\vec{P}+\vec{Q}=-3\hat{i}$, what is their magnitude?}

\text{Town B is $50.0 \mathrm{~km}$ east of town A. Starting from town A, you drive your car $24.0 \mathrm{~km}$ in }

\text{a direction $15.0^{\circ}$south of east and then you drive $18.0 \mathrm{~km}$ due north.}

\text{What is the minimum distance between your final location and town B? }

{\text{A) $29.3 \mathrm{~km}$}}\\ \text{B) $38.0 \mathrm{~km}$}\\ \text{C) $26.8 \mathrm{~km}$}\\ \text{D) $33.2 \mathrm{~km}$}\\ \text{E) $42.6 \mathrm{~km}$}\\

\text{(Important for exam)}

\text{It is better in such situation to work with the components}

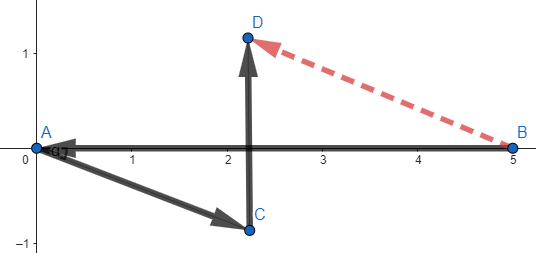
\displaystyle \overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{CD}

\text{We have:}

\text{Let us use the components:}

\overrightarrow{BA}=(-50,0)

\overrightarrow{AC}=(24 \cos(-15^\degree),24 \sin(-15^\degree))

\overrightarrow{CD}=(0,18)

\text{By summing the components, we get:}

\overrightarrow{BD}=(-26.8,11.8)

\text{The distance BD is therefore: } BD=\sqrt{26.8^2+11.8^2}=29.3

\text{Town B is $50.0 \mathrm{~km}$ east of town A. Starting from town A, you drive your car $24.0 \mathrm{~km}$ in }

\text{a direction $15.0^{\circ}$south of east and then you drive $18.0 \mathrm{~km}$ due north.}

\text{What is the minimum distance between your final location and town B? }

\text{(Important for exam)}

\text{Answer A}

\text{Find the magnitude B if the magnitude of $\vec{A} \times \vec{B}$ is 4.0 units and $\vec{A} \cdot \vec{B}=3.0$ units.}

{\text{A) $2.3 \mathrm{~units}$}}\\ \text{B) $3.0 \mathrm{~units}$}\\ \text{C) $2.8 \mathrm{~units}$}\\ \text{D) $3.2 \mathrm{~units}$}\\ {\text{E) $1.7 \mathrm{~units}$}}\\

\text{Vector $\vec{A}$ has a magnitude of 3.0 units. Vector $\vec{B}$ has a magnitude of $\mathrm{B}$ units. }\\

\vec{A}.\vec{B}=3

|\vec{A}\times \vec{B}|=4

AB \cos\theta=3

AB \sin\theta=4

\Rightarrow

\text{If I square the two equations and then sum them I will get}

(AB)^2(\cos^2\theta+\sin^2\theta)=3^2+4^2=25

(AB)^2=5\Rightarrow AB=5\Rightarrow B=5/A=1.66 \text { units}

\text{because }(\cos^2\theta+\sin^2\theta)=1

\text{Find the magnitude B if the magnitude of $\vec{A} \times \vec{B}$ is 4.0 units and $\vec{A} \cdot \vec{B}=3.0$ units.}

\text{Vector $\vec{A}$ has a magnitude of 3.0 units. Vector $\vec{B}$ has a magnitude of $\mathrm{B}$ units. }\\

\text{Answer E}

\text{Can you solve this old exam?}

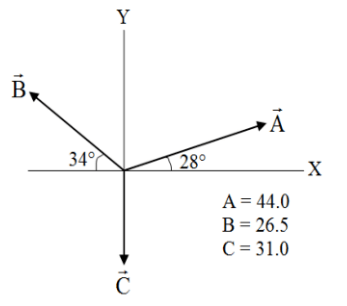
\text { For the three vectors }(\vec{A}, \vec{B}, \vec{C}) \text { shown in Figure } 2 \text {, find } \vec{C} \times(\vec{A} \times \vec{B}) \text {. }

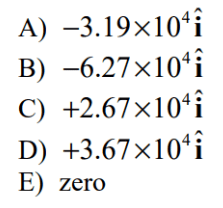
\begin{align*} &\text{Calculate } (\vec{A} \times \vec{B}) \cdot \vec{C} \text{ for three vectors } \vec{A}, \vec{B}, \text{ and } \vec{C}. \text{Vector } \vec{A} \text{ has magnitude } 6.00~\text{m}\\ &\text{an angle } \theta_A = 20.0^\circ.\text{Vector } \vec{B} \text{ has magnitude } 5.00~\text{m and angle } \theta_B = 60.0^\circ.\text{ Angles are} \\ &\text{measured counterclockwise from the } +x\text{-axis.}\text{Vector } \vec{C} \text{ has magnitude 4.00~\text{m} and } \\ &\text{points in the } +z\text{-direction,} \text{while vectors } \vec{A} \text{ and } \vec{B} \text{ lie in the } xy\text{-plane.}\\ &\\ &A) \hspace{2mm}77.1~\text{m} \\ &B) \hspace{2mm}79.5~\text{m} \\ &C) \hspace{2mm}87.4~\text{m} \\ &D) \hspace{2mm}91.2~\text{m} \\ &E) \hspace{2mm}99.0~\text{m} \end{align*}

\begin{align*} &\text{Calculate } (\vec{A} \times \vec{B}) \cdot \vec{C} \text{ for three vectors } \vec{A}, \vec{B}, \text{ and } \vec{C}. \text{Vector } \vec{A} \text{ has magnitude } 6.00~\text{m}\\ &\text{an angle } \theta_A = 20.0^\circ.\text{Vector } \vec{B} \text{ has magnitude } 5.00~\text{m and angle } \theta_B = 60.0^\circ.\text{ Angles are} \\ &\text{measured counterclockwise from the } +x\text{-axis.}\text{Vector } \vec{C} \text{ has magnitude 4.00~\text{m} and } \\ &\text{points in the } +z\text{-direction,} \text{while vectors } \vec{A} \text{ and } \vec{B} \text{ lie in the } xy\text{-plane.}\\ \end{align*}

\text{Method I}

(\vec{A} \times \vec{B}) \cdot \vec{C}=|(\vec{A} \times \vec{B})| . C= A B \sin(\theta_{AB}) C

\text{Using the right hand rule, we deduce that the vectror $\vec{A}\times \vec{B}$ is in the +$z$-direction}

\text{so, the angle between $\vec{C}$ and $(\vec{A}\times \vec{B})$ is zero}

\theta_{AB}=60^\circ-20^\circ=40^\circ

= 120\sin{40^\circ}=77.1~\mathrm{m}

\text{Method II}

\vec{A}=\left[\begin{array}{l} A \cos\theta_A\\ A \sin\theta_A \\ 0 \end{array}\right]= \left[\begin{array}{l} 5.64\\ 2.05 \\ 0 \end{array}\right]

\vec{B}=\left[\begin{array}{l} B \cos\theta_B\\ B \sin\theta_B \\ 0 \end{array}\right]= \left[\begin{array}{l} 2.50\\ 4.33 \\ 0 \end{array}\right]

\vec{C}=\left[\begin{array}{l} 0 \\ 0 \\ 4 \end{array}\right]

\vec{A}\times\vec{B}=\left[\begin{array}{l} 0 \\ 0 \\ 19.3 \end{array}\right]

(\vec{A} \times \vec{B}) \cdot \vec{C}= \left[\begin{array}{l} 0 \\ 0 \\ 19.3 \end{array}\right] \cdot \left[\begin{array}{l} 0 \\ 0 \\ 4 \end{array}\right] =77.1