Cálculo de la Complejidad de Kolmogorov vía AG
Fernanda Mora
Aarón Sánchez
Luis E. Pérez
11 diciembre del 2015
Any darn fool can make something complex; it takes a genius to make something simple.
-Pete Seeger
Contenido
- Antecedentes
- Metas
- Programa
- Resultados
- Bibliografía
Antecedentes
Motivación
Any darn fool can make something complex; it takes a genius to make something simple.
-Pete Seeger
- Teoría de la Información: Estadística y Algorítmica
- Proyecto 1: Estadística con Shannon
- Proyecto final: Algorítmica con Kolmogorov
- Además, máquinas de Turing, funciones incomputables y algoritmos genéticos
¿Qué se va a estudiar en este proyecto?
Proceso de transmisión de la información
Envío y pérdida de información mediante sistema de información
También vimos en clase:
Si algo se puede cuantificar, entonces se puede codificar.
Si algo se puede codificar, entonces se puede hacer el código binario asociado.
Entonces, cualquier información puede ser expresada con código binario.
Un código binario se puede almacenar y enviar.
Para llevar a cabo la transmisión se requieren recursos temporales y de almacenamiento.
Surge naturalmente una pregunta:
¿Cuál es la mejor manera de representar un conjunto de datos a modo de minimizar los recursos necesarios?
- Tenemos primero que determinar la cantidad de información contenida en los datos: Shannon?
-
2 desventajas:
-
Asume que conocemos la distribución de probabilidades en la fuente.
- Asume que la fuente es ergódica (estacionaria y si todo arreglo posible en una muestra aparece tantas veces como dice su disitribución estacionaria). El problema con esto es que la ergodicidad depende de la manera en como definamos un símbolo
-
Asume que conocemos la distribución de probabilidades en la fuente.
¿Cómo le hacemos?
Propuesta alternativa: Kolmogorov
- Andrey Kolmogorov tomó una ruta alternativa y definió la información en un mensaje como la longitud en bits del programa más pequeño que puede reproducir el mensaje y a esto le llamó información algorítmica
- También conocida como Complejidad de Kolmogorov
- Esta es la idea central de donde parte la Teoría de la Información Algorítmica que mencionamos en la introducción.
Exploremos el concepto
-
En la definición estamos hablando de un programa: ¿en qué lenguaje? ¿con qué máquina?
-
Para lograr generalidad, Kolmogorov estableció que dicha máquina tenía que sea una máquina de Turing.
Definición 1.- (Kolmogorov (1965), Chaitin (1966)). La información algorítmica, también llamada Complejidad de Kolmogorov de una cadena s es la longitud del programa más pequeño p que produce a s en una máquina de Turing universal U.
Es decir, K(s)={min|p| : U(p)=s}
Definición (Kolmogorov 1965-Chaitin 1966)

Teorema 1.- Sea M un mensaje tal que en un lenguaje C encontramos el programa P más pequeño que reproduce M con una longitud dada por L(C). Sea C' otro lenguaje y P' el programa más pequeño que reproduce M con una longitud dada por L(C').
Entonces |L(C)-L(C')|<a para alguna a constante con a>=0.
Es decir, la información algorítmica es independiente del lenguaje salvo por constantes aditivas
Realmente no importa el lenguaje que escojamos
Algunos resultados
3 importantes dificultades surgen al considerar la complejidad de Kolmogorov:
-
Incomputabilidad
-
Imposibilidad de la aleatoriedad
- Inestabilidad
Algunas dificultades
Teorema 2.- Calcular la Complejidad de Kolmogorov para un mensaje arbitrario es un problema incomputable.
1. Incomputabilidad
- No existe un algoritmo que pueda decir si un programa p que genera s es el más pequeño
- Es imposible calcular en una cantidad acotada de tiempo la información algorítmica para un mensaje arbitrario
- La complejidad de Kolmogorov sólo puede ser aproximada en la práctica.
Implicaciones del Teorema 2
2. Imposibilidad de la aleatoriedad
- Una cadena con una complejidad algorítmica baja se puede comprimir mucho: es posible codificar la información que contiene mediante un programa con una longitud mucho más pequeña
- Encontrar el programa más pequeño que replique el mensaje original descansa del hecho de que es posible encontrar regularidades-patrones en el mensaje original y entonces la CK es más pequeña que el mensaje original, de modo que es posible comprimir el mensaje
- Entonces, la CK de una cadena mide su aleatoriedad: más complejidad implica menor posibilidad de compresión y mayor aleatoriedad.
2. Imposibilidad de la aleatoriedad
- Una sucesión aleatoria no se debe poder comprimir y un mensaje comprimido lo máximo posible debería parecer una sucesión aleatoria
- Para calcular la CK tenemos que buscar algoritmos que puedan detectar patrones en el mensaje y que logren comprimirlo para que “parezca” una sucesión aleatoria.
2. Imposibilidad de la aleatoriedad
- A pesar de que la compresión y la aleatoriedad están relacionadas, no es posible decir que una sucesión es realmente aleatoria
- ¿Por qué? porque esto implicaría poder calcular K(s) de manera exacta y compararla con la longitud de s.
2. Imposibilidad de la aleatoriedad
- Pero sí podemos es mostrar que una sucesión no es aleatoria si podemos encontrar un programa de una longitud menor a la sucesión
- Entonces, es posible acotar superiormente a K(s) y s no puede ser más compleja que la longitud del programa mucho más chico conocido que genere a s.
La mayoría de las sucesiones no son aleatorias
Resultado: Hay más sucesiones no aleatorias que aleatorias.
Esbozo de prueba:
- Existen exactamente cadenas de bits de longitud
- Sólo hay cadenas con menor número de bits
- Existen considerablemente menos programas cortos que programas largos.
- No podemos parear a todas las cadenas de longitud n con programas de longitud mucho menor, pues no hay suficientes programas pequeños para codificar a todas las cadenas más largas
- CK depende de la máquina de Turing: K(s)=min{|p| : U(p)=s}
- ¿Es posible que si ?: Sí.
- Más inestable para cadenas cortas.
3. Inestabilidad
- Complejidad de Kolmogorov: La CK de un número n es el menor número de estados que se necesitan para que un Castor Ocupado que para con un bloque de n 'unos' consecutivos en una cinta inicialmente en blanco.
Definición alternativa
Metas
¿Qué queremos hacer ?
- Entregable final: obtener una aproximación de la Complejidad de Kolmogorov para cadenas pequeñas. Esto requiere encontrar la máquina de Turing más pequeña que replique la cadena.
- Esta tarea se puede ver como un problema de optimización.
- Los algoritmos genéticos son una acertada elección cuando el espacio de búsqueda es prohibitivamente grande o cuando tenemos poca idea del espacio solución.
- Monte-M. Conte, I. De Falco [3] “el enfoque evolutivo ha ayudado a resolver los problemas relativos a tiempo y espacios intractables que generalmente ocurren con los métodos que tratan de aproximar la función de complejidad de Kolmogorov”.
¿Qué queremos hacer ?
- Entonces el problema se planteó como un problema de optimización a resolver vía un algoritmo genético con una población inicial de Máquinas de Turing.
- ¿En qué consiste dicho problema? En encontrar la máquina de Turing que al ser corrida genere una sucesión que se parezca “lo más posible” a la cadena original.
- Hay que definir a qué nos referimos con “parecerse lo más posible” a la cadena original. Luego, hay que proponer una función de fitness entre la cadena de entrada y la cadena generada por una máquina de Turing.
Metodología
- El algoritmo genético que se usó fue el canónico, el cual fue propuesto por John Holland en 1965.
- A continuación se muestra el proceso usual de evaluación en un algoritmo genético.
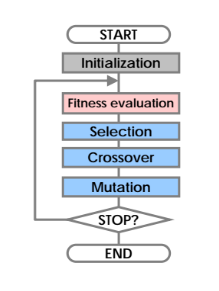
Metodología
- Se programó un AG simple que
