Solving Rubik's Cubes
with F#
Stachu Korick | @stachudotnet | hello@stachu.net
Nov 17, 2018
Talk Inspiration
- Speed-Solving Rubik's Cubes
- And other pattern-related hobbies
- Writing F#
A bit about me
Stachu
site: stachu.net
.NET
email: hello@stachu.net
github: @stachudotnet
facebook: @stachudotnet
twitter: @stachudotnet
The Plan
- [10] (this) Intro
- [10] On-Ramp Domain Knowledge
- [15] Hands-on: How to represent and "turn" a cube?
- [15] Hands-on: How to scramble a Rubik's Cube?
- [15] Show off Inefficient Solvers
- (the Rubik's Cube is a "graph"!)
- [30] Discuss Efficient Solver Patterns
- (sure, but it's also a "group"!)
- [10] Show off SAFE usage (Fable+Elmish+Saturn)
- Hands-on opportunities!
- [10] Outro/Questions/Buffer
- (probably related to the Rubik's Cube speed-solving world)
A bit about the Rubik's Cube
My Cubing Background

My Cubing Background
The Physical Structure, Pt. 1
The core structure of the Rubik's Cube does not move relative to each

The Physical Structure, Pt. 2
12 Edges surround the core and the centers.
Each of these 12 pieces has two orientations; "correct" and "flipped."
An edge cannot have opposite-side colors.
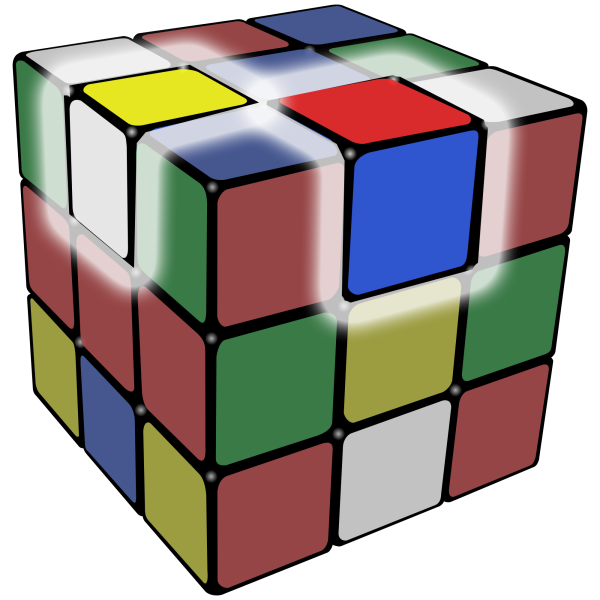
The Physical Structure, Pt. 3
8 "corner" pieces surround the core and edges.
Each of them has 3 orientations: "correct," "twisted clockwise" and "twisted counter-clockwise."
These also cannot have two "opposite" colors.

Basic 6 Moves
- R(
ight ) - L(
eft ) - U(p)
- D(own)
- F(
ront ) - B(ack)
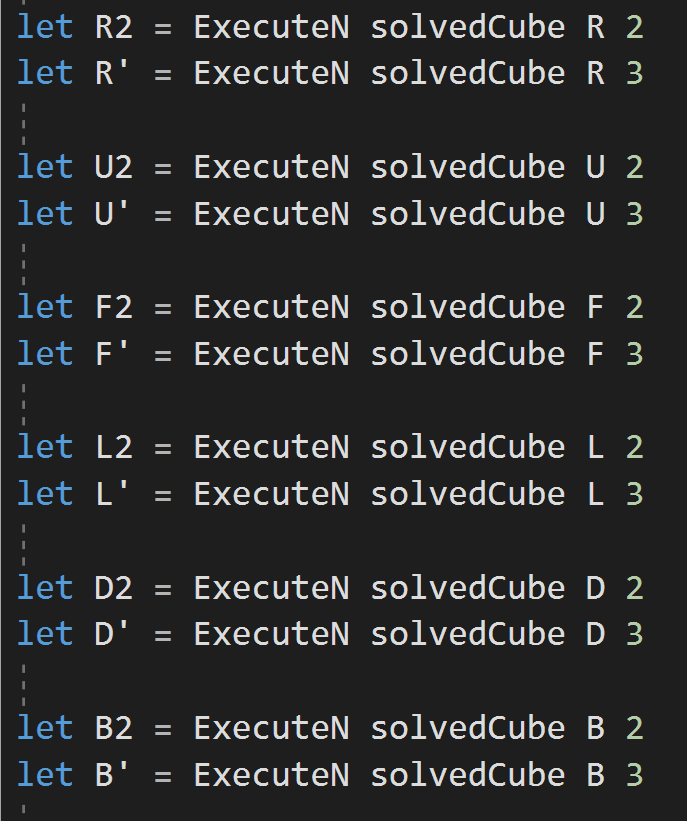
12 Derived Moves
- R is clockwise 90 degrees
- R' is counter-clockwise 90 degrees.
- R2 is the R face turned 180 degrees.
- ...
An Example Algorithm
Referring to
Certain Pieces
Creating a Simple Solver
-
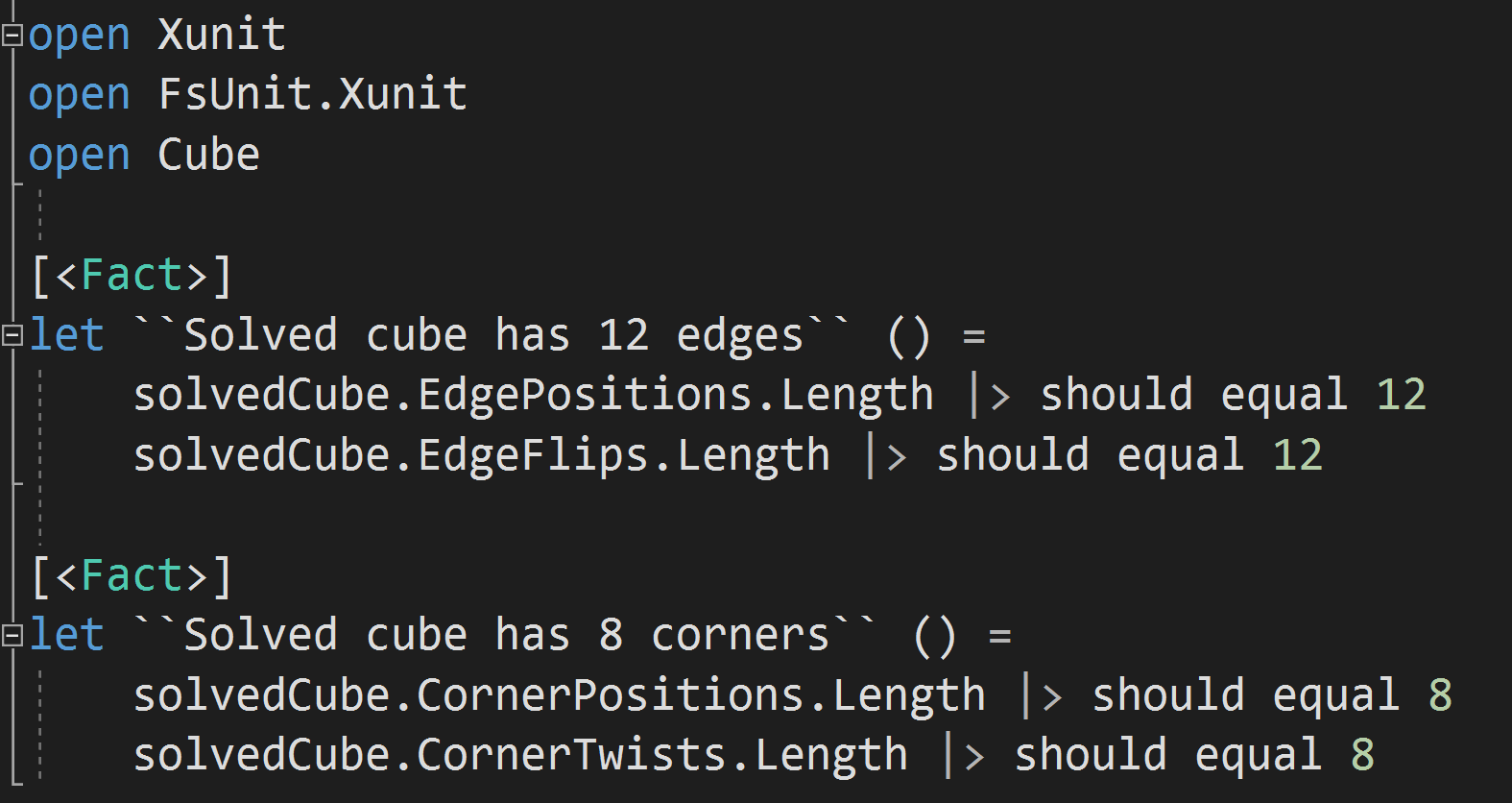
Modeling the cube's state
-
Writing a scrambler
-
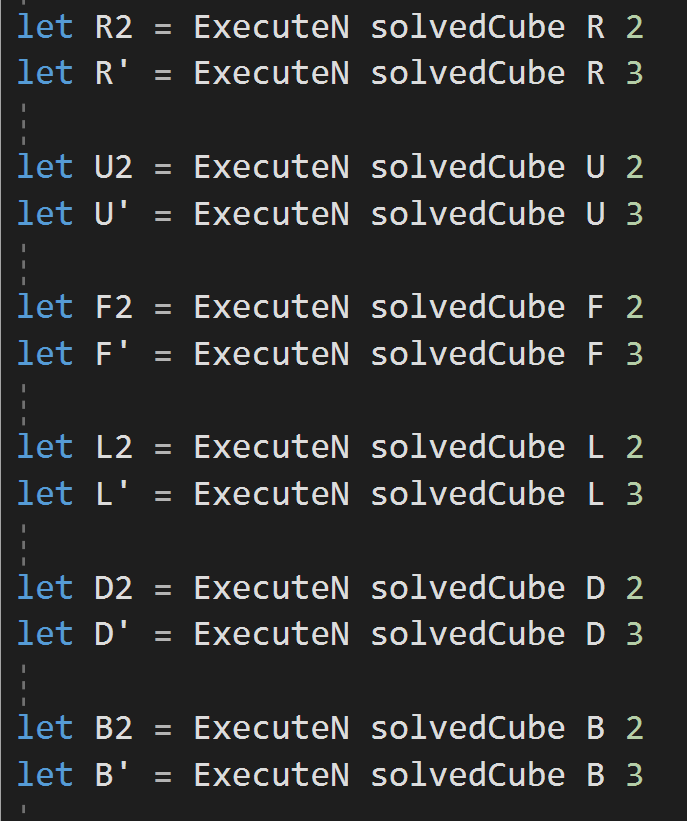
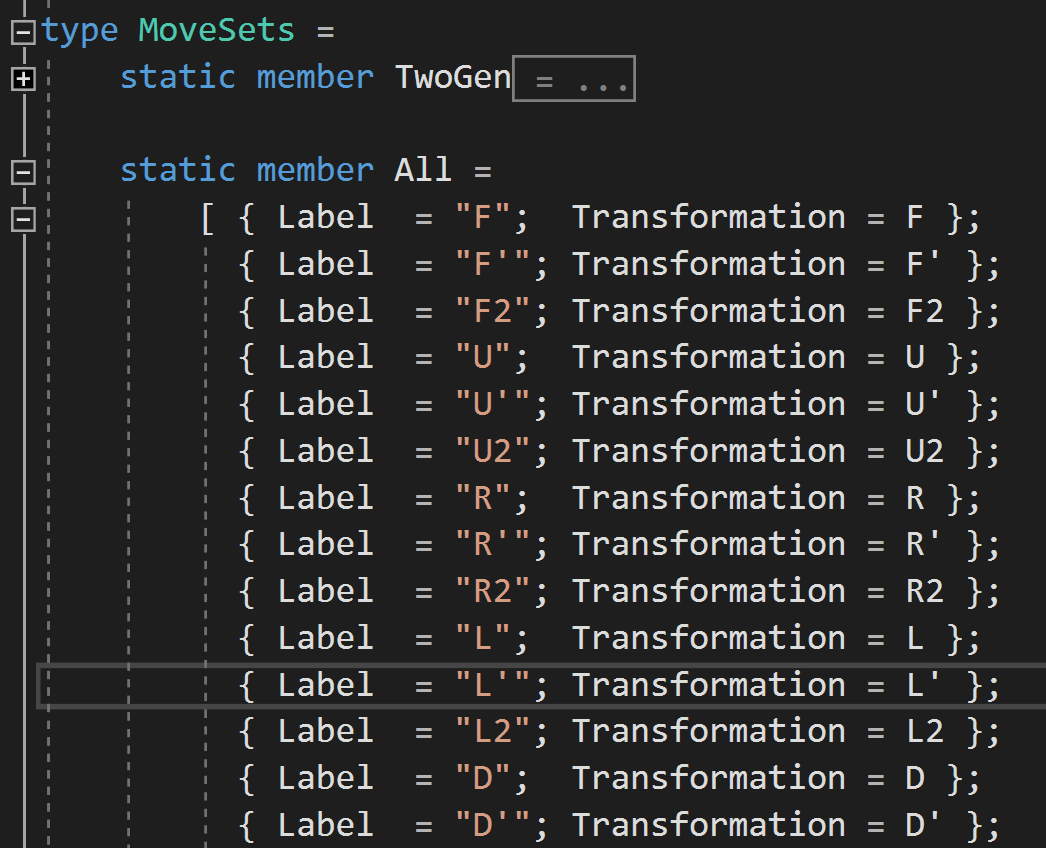
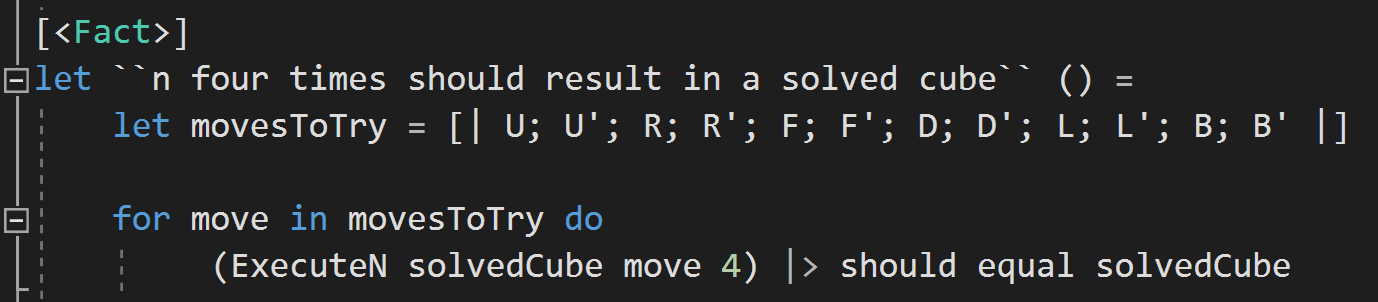
Transcribing the basic 18 'moves'
-
Getting *some* solver running
Challenge!
How can you store the state of a Rubik's Cube?
Representing the Cube
Facelet
Facelet Array
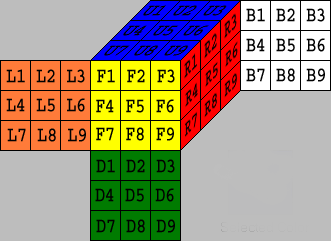
Representing the Cube
Cubie
Piece Arrays
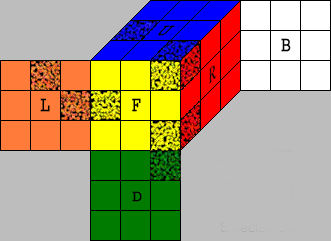
Representing the Cube
CO+CP+EO+EP
CO + CP + EO + EP
CO: 0 <= x1 < 3^7
EO: 0 <= x2< 2^11
CP: 0 <= x3< 8!
EP: 0 <= x4< 12!
Representing the Cube
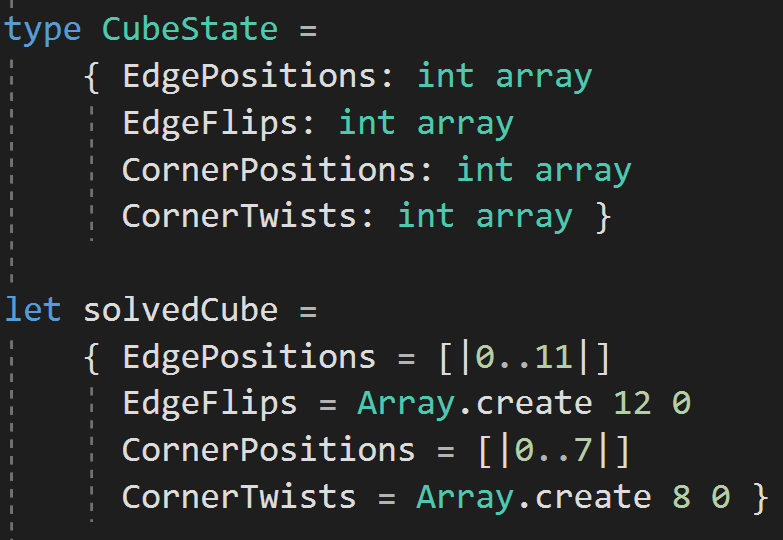
Representing the Cube
Turning the Cube
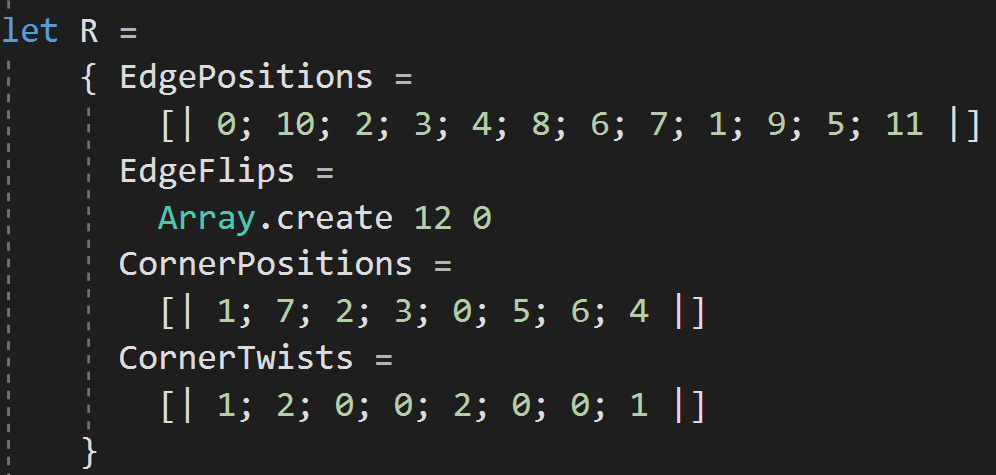
Turning the Cube
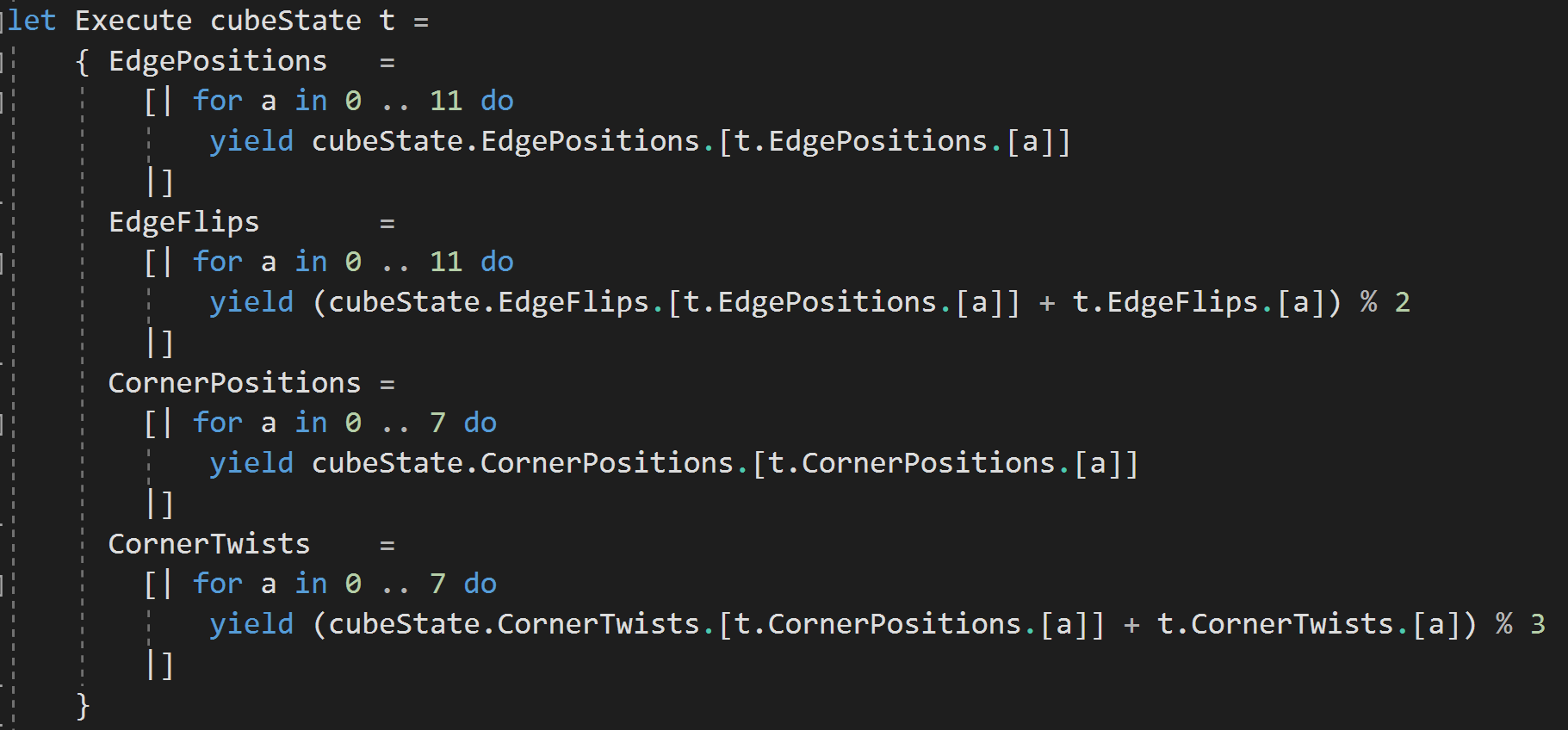
Turning the Cube

Turning the Cube
Turning the Cube
Turning the Cube

Turning the Cube
Challenge!
Scramble a Rubik's Cube
Scrambling the Cube
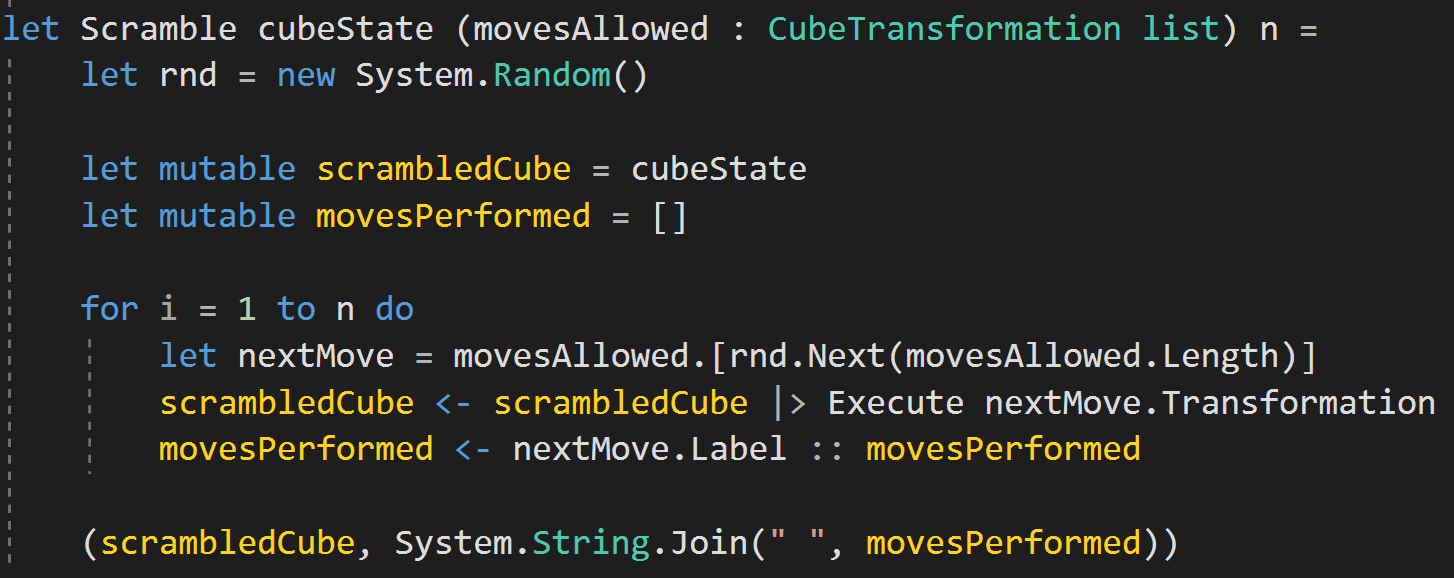
Scrambling the Cube

The Cube is a Graph






R2 U2
R2
U2
U2 R2
U2 R2 U2 R2 U2 R2

U2 R2 U2

U2 R2 U2 R2

U2 R2 U2 R2 U2



R2 U2 R2
R2 U2 R2 U2
R2 U2 R2 U2 R2
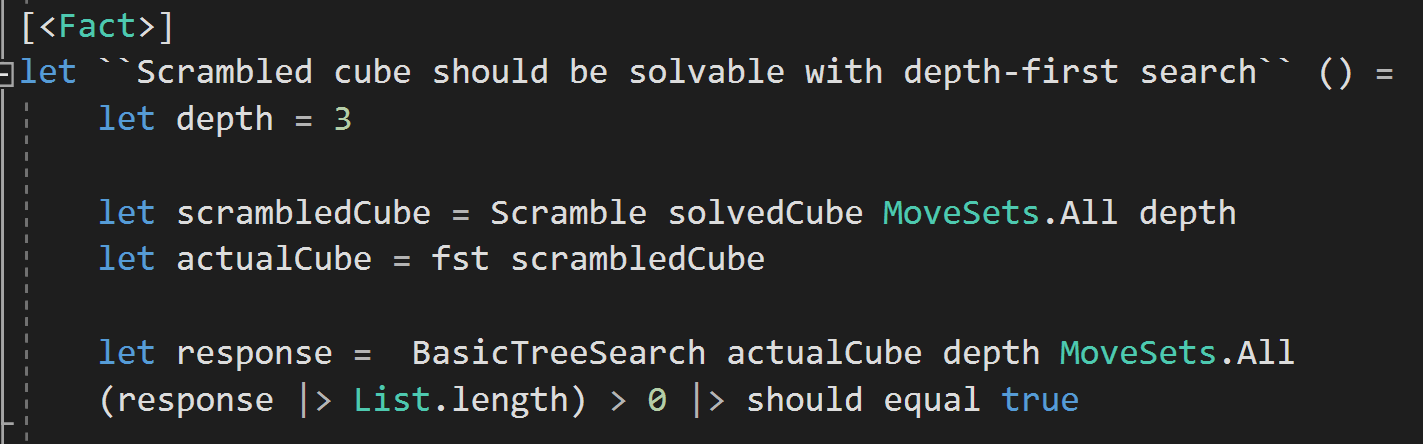
Depth-First Tree Searching
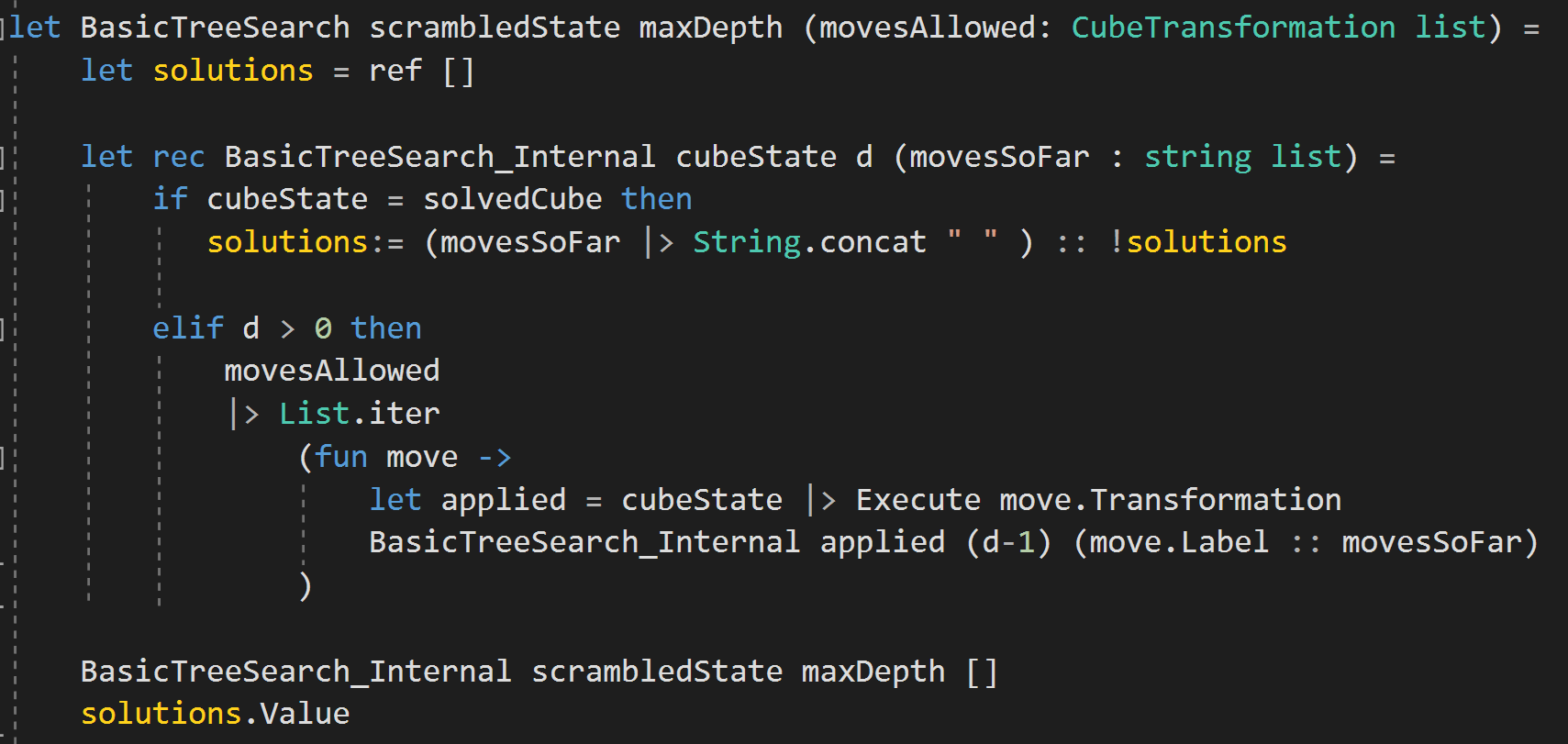
Depth-First Tree Searching
IDA Tree Searching
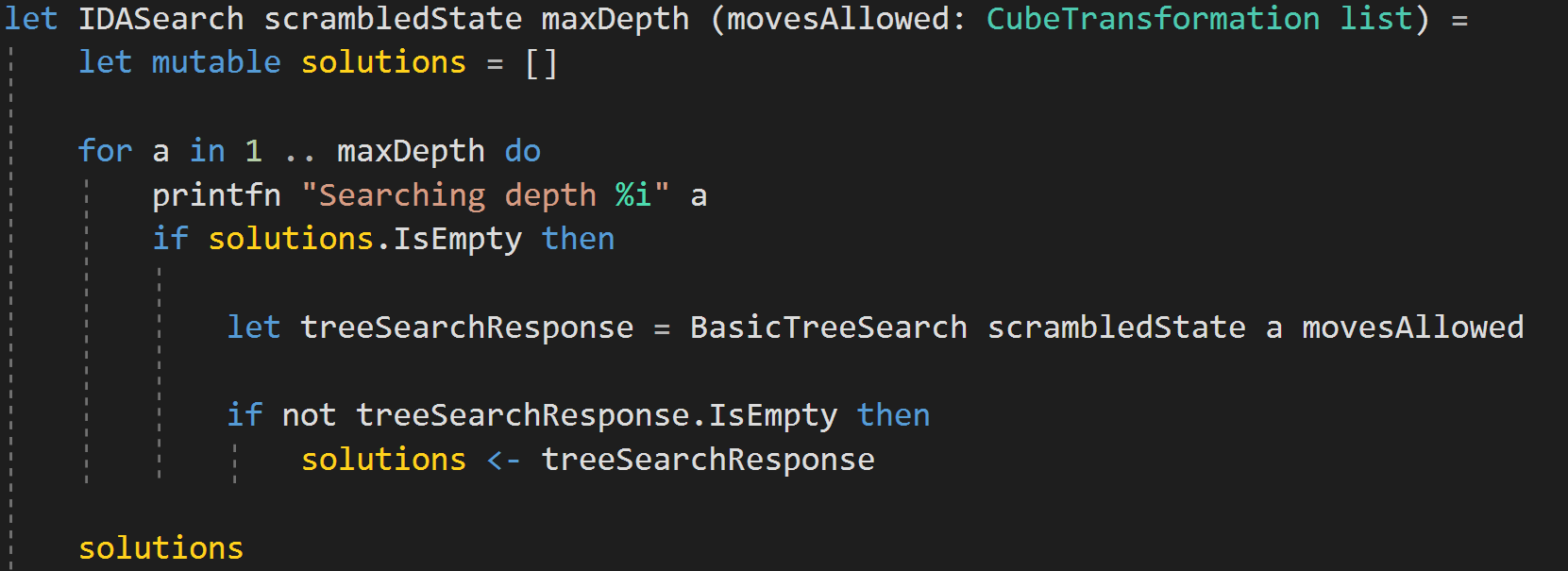
Why is this so slow?
- 43 quintillion is a big number. (really big)
- 18^20 is a big number. (even bigger)
- `Execute` takes a while to change cube state
Creating a Better Solver
Some Trade-offs for Consideration
- Human-Learnable
- Turning Ergonomics
- Support partially-defined cubes?
- Move Count
- Resource Requirements
- CPU, RAM, Disk Storage
- Speed
Program Human Algorithms?
The "CFOP" Method



Cross
F2L
(First 2 Layers)
OLL
(Orientation of the Last Layer)
PLL
(Permutation of the Last Layer)
Creating a Complex Solver
focus: run in a reasonable amount of time
The Kociemba Algorithm
Phase 1
Phase 2
Solved:
- Edge Orientation
- Corner Orientation
- U/D Edges in U/D Layer
Solve the rest, using only <U,D,R2,L2,F2,B2>
Additional "tricks"
to Implement
- representing each of these components into simple 16-bit integers
(16bits is a lot less than an int array!) - move depth-caching caching
(how many moves deep various positions are away from a 'solved' state) - caching position-transitions
- storing the transitions between the 16bit numbers rather than computing them on the fly
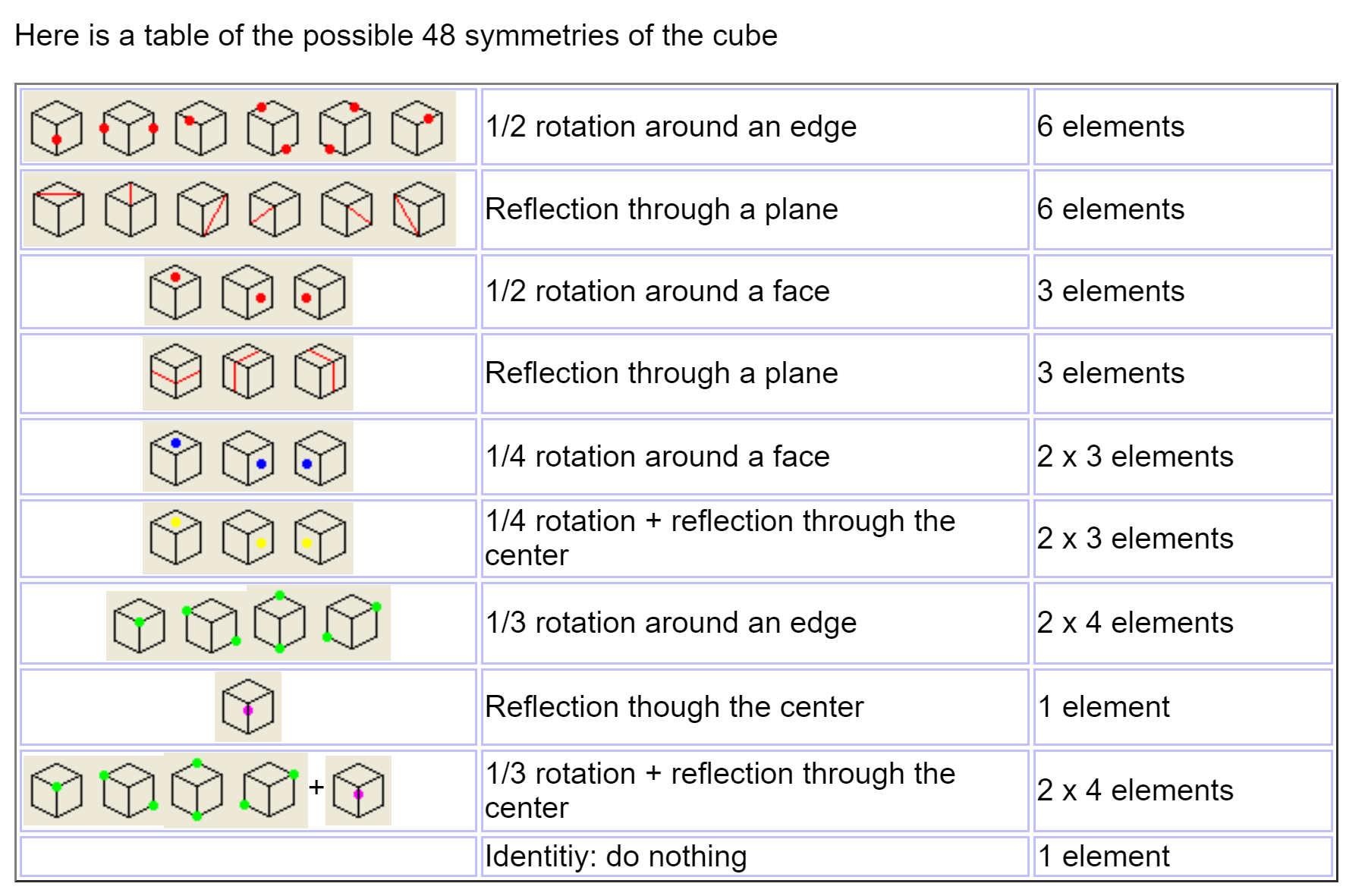
- taking advantage of symmetries
- using sub-optimal phase 1 solutions
Storing Cube State Cheaply

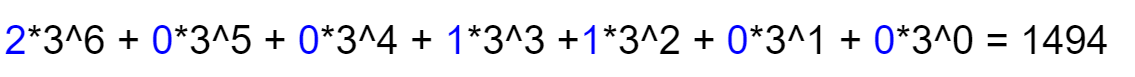
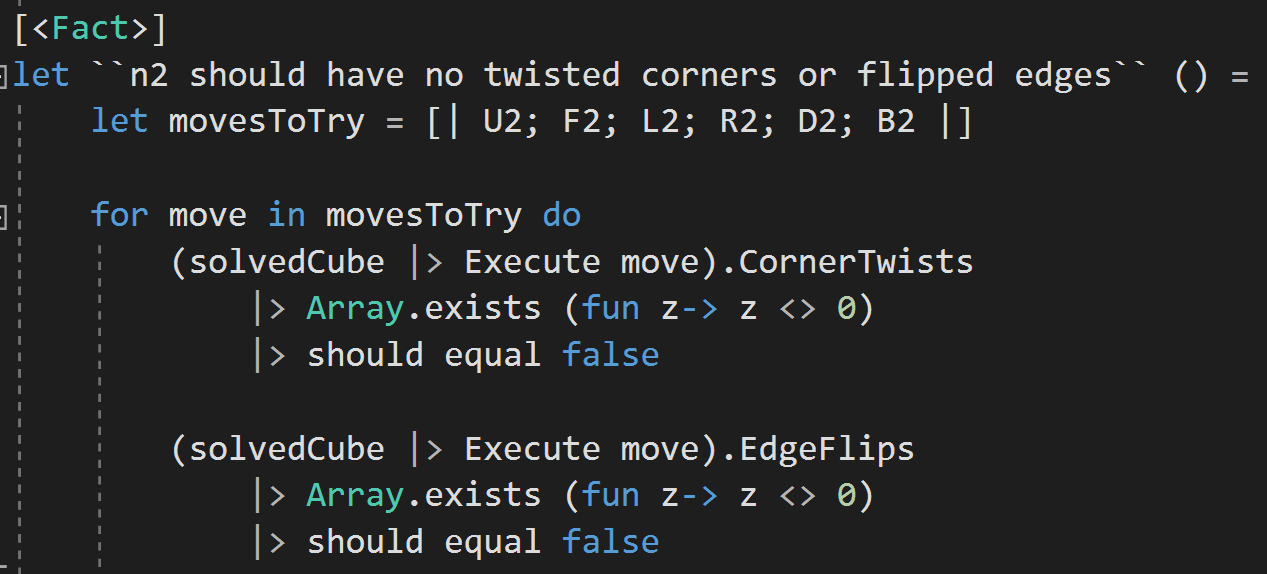
Corner Orientation
Storing Cube State Cheaply
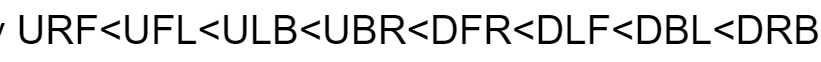
Corner Permutation

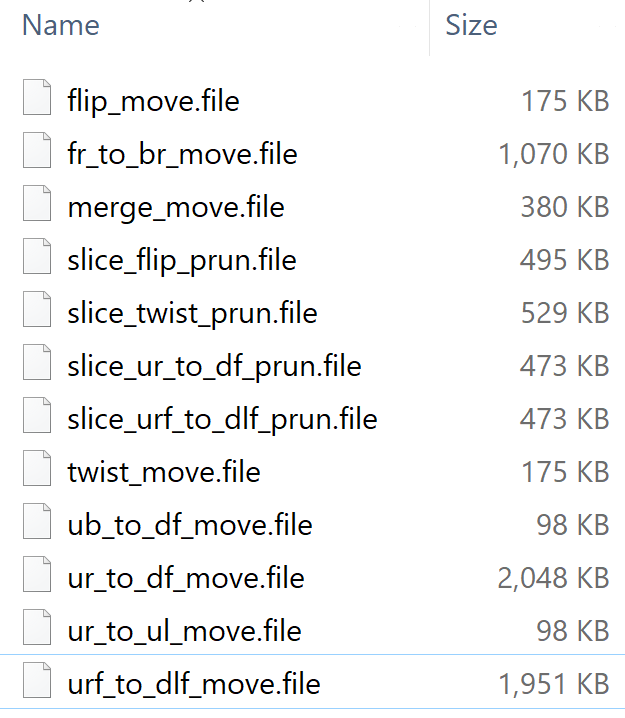
Move Tables
Symmetry Reductions
Pruning Tables
function Treesearch(position p, depth d)
if d = 0 then
if p is solved then
Hooray!
else if d > 0 then
if prune1[p] <= d and prune2[p] <= d then
for each available move m
Treesearch(result of m applied to p, d-1)
Pruning Tables
Using Sub-Optimal Phase 1 Solutions
Let's See It in Action!
Running it all with SAFE

Thanks! Questions?
@stachudotnet on twitter and
(hello@)stachu.net
Topic suggestions:
- What other puzzles are featured at competitions?
- Can you tell us a cubing story or two?
- How do people solve them blindfolded?
- Are you ever going to record another WTF# episode?