Computational Protein Design

Proteins

Proteins are sequences of amino acids that are essential to many bodily functions.

 

Protein structure is closely related to protein function.

 

Individual amino acids attract/repel one another.

 

The protein tends to fold into conformations that minimize its free energy.

What is Computational Protein Design?

Computational Protein Design (CPD) tries to, given a protein structure, find an amino acid sequence that will likely fold into that structure. It is the inverse of the problem of protein folding.

 

After we know a sequence, we can make that protein in the lab.

 

CPD has already been used to design proteins for important medical applications (like detecting HIV) and holds promise to treat diseases that involve complex protein-protein interactions (Alzheimer's, cancer, etc.).

Quantum Annealing

Quantum Computing

Quantum computing is the use of quantum-mechanical phenomena to perform computation.

 

The basic unit of quantum computation is the qubit.

Systems of qubits exhibit superposition and entanglement to explore a large solution space.

 

Lots of promise, even more hype, but experimental results have been limited to small or artificial problems.

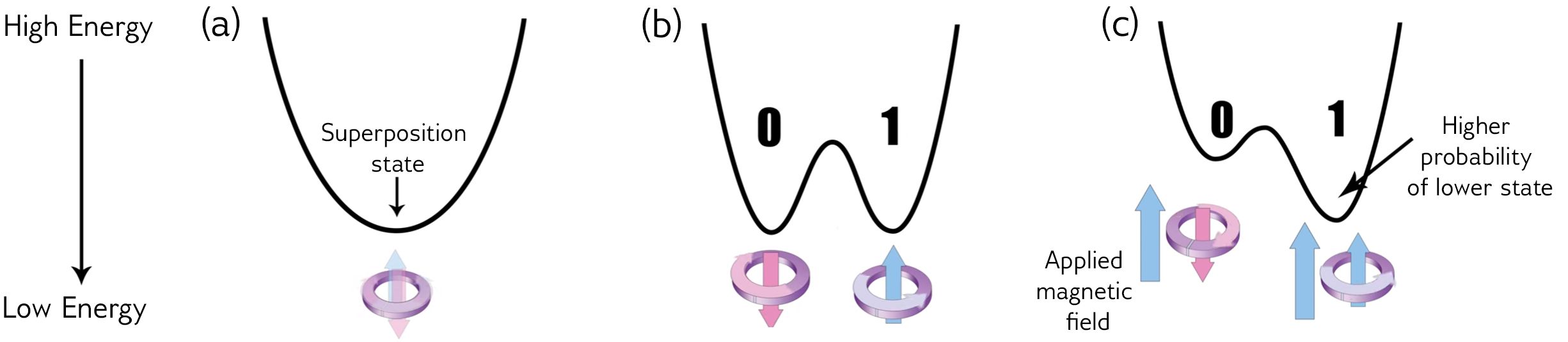
What is Quantum Annealing?

Quantum annealing is a type of quantum computation that does one job: optimizing functions.

 

It represents the objective function with a system of qubits where the function's output corresponds to the energy of the system.

It then evolves the physical system to find the ground state according to the adiabatic theorem (plus noise).

The D-Wave Quantum Computer

The D-Wave machine only solves quadratic unconstrained binary optimization (QUBO) problems:

$$\min_{x \in \{0,1\}^n} x^T Q x$$

where Q is the matrix that defines the problem, and x is a binary solution vector.

 

Entries of the matrix Q are represented by coupling strengths between qubits, and the solution vector x is encoded in the spin (up - 0 or down - 1) of the qubits. So as the annealer evolves to the lowest energy state of the system, it also solves the optimization problem.

Solving a CPD Problem on the

D-Wave

Motivation

This is an NP-hard discrete optimization problem.

The dominant approach (used by Rosetta) is simulated annealing, but this struggles with >100 residues and requires huge computational resources.

 

Scientists want a low-energy sampling distribution rather than one optimal solution - and the D-Wave is essentially an efficient low-energy probabilistic sampler.

 

Currently, protein design requires lots of intuition even with computational methods, but by improving these methods, we are hoping to take some of the guesswork out of design.

As a QUBO

We use Rosetta to calculate an energy matrix for different amino acid values.

 

We introduce penalties to this matrix to ensure we assign one amino acid per position.

 

The binary solution vector represents an amino acid sequence.

 

So we solve for the lowest energy amino acid sequence

$$\min_{x \in \{0,1\}^n} x^T Q x$$

Solving Larger Problems

While the D-Wave 2000 series has 2000 qubits, they are so sparsely connected that we can only fit a 100 variable CPD problem on a single chip.

 

To solve larger problems, we use a hybrid strategy.

This iterative solver alternates between two methods as it attempts to converge to a global minimum:

1. classical heuristic local search (ex. simulated annealing)
2. quantum annealing subproblem solver

 

With this method we get good results on 2000-3000 variable (20-30 residue) problems.

What We Did

Collaborators' Work

We collaborated with Vikram Mulligan and a computer scientist with a physics background (Hans Melo) who had been working on this problem for about a year already.

 

In that time, they developed and implemented the mapping from CPD problem to QUBO matrix, and generated ~6,000 CPD problems of various sizes to test on the D-Wave.

 

They also solved a 33-residue design problem using the hybrid quantum-classical approach, and are currently expressing it in the lab to verify the solutions experimentally.

A Peptide Designed on a Quantum Comuter

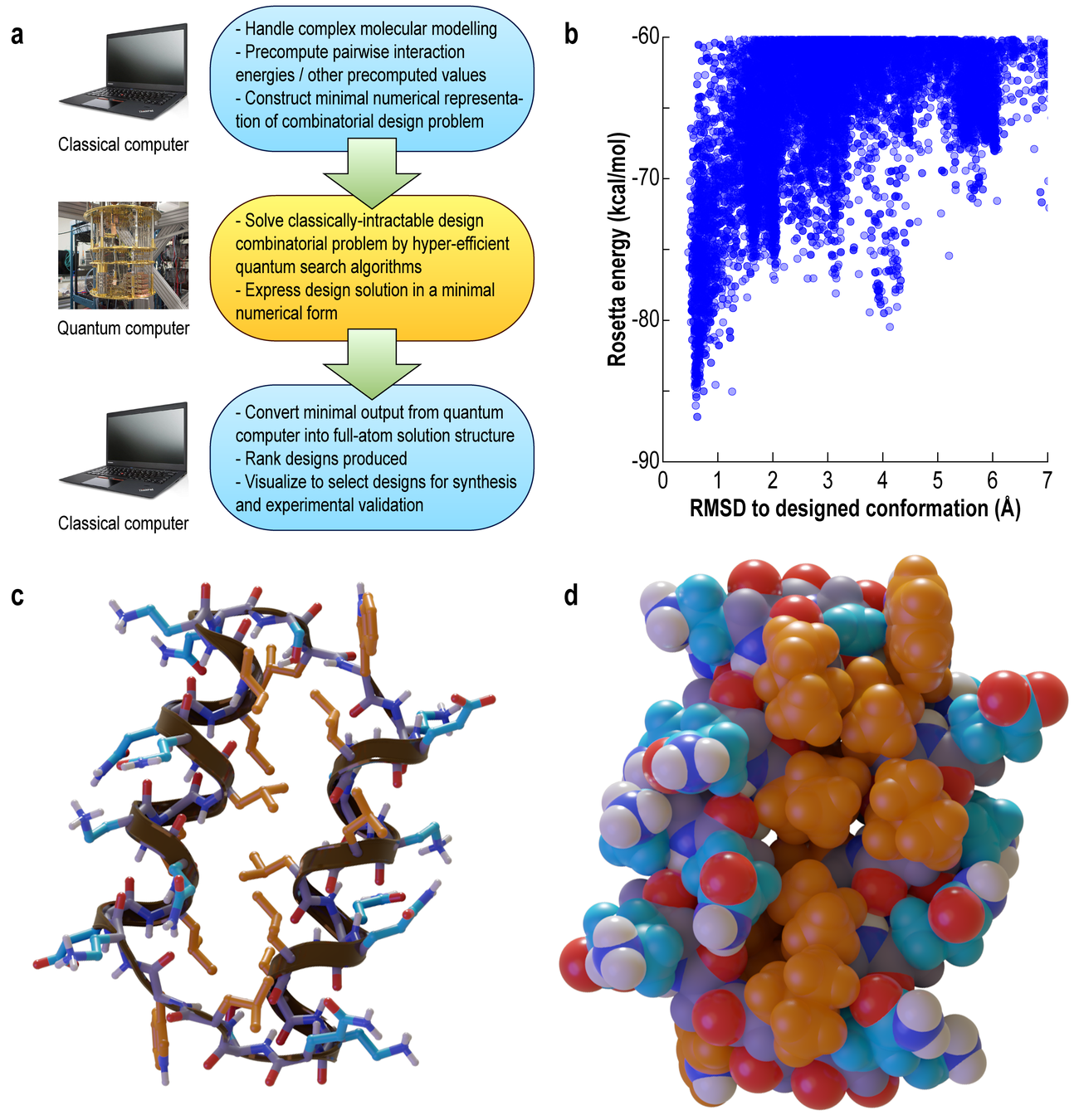
33 residue

quantum-designed protein

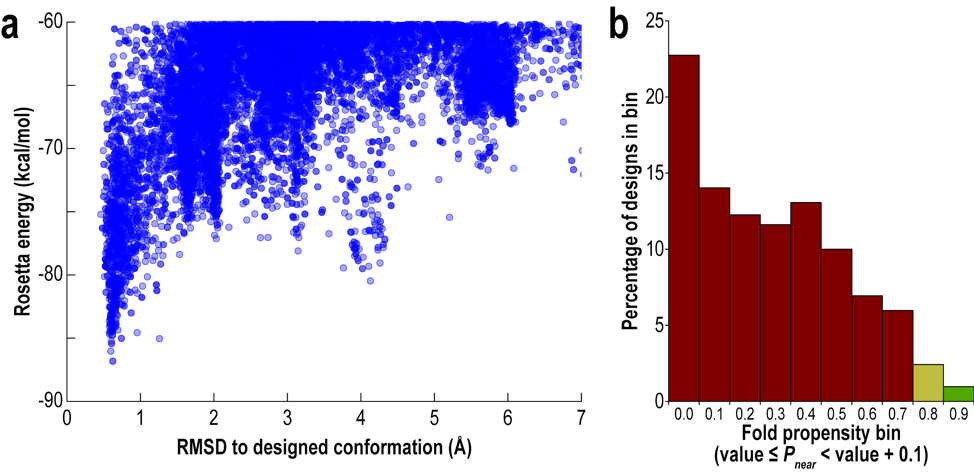
Well-separated low-energy solution implies stability of the design

The following scaling conclusions have caveats and need to be refined.

Scaling of Quality of Solution

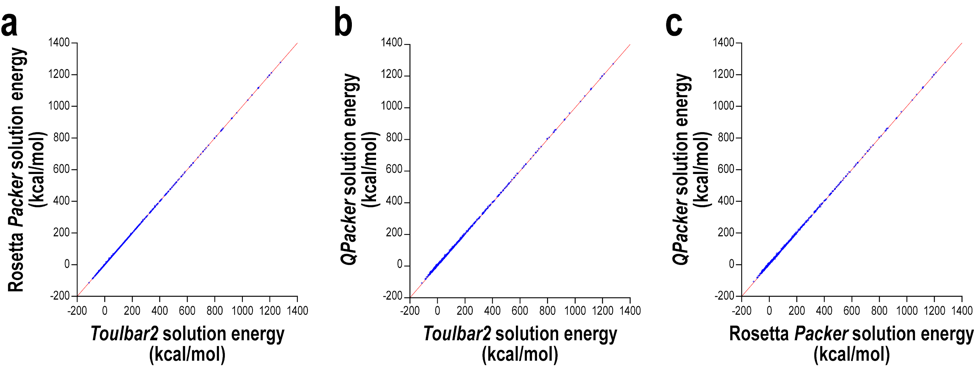
Blue points represent QPacker solution energy vs Toulbar2 (an exact solver) solution energy on 622 design problems.

 

QPacker solutions are not always optimal but are reasonably close (on line y=x).

 

Question: how does probability of experimental success scale with problem size?

Scaling of Time to Solution

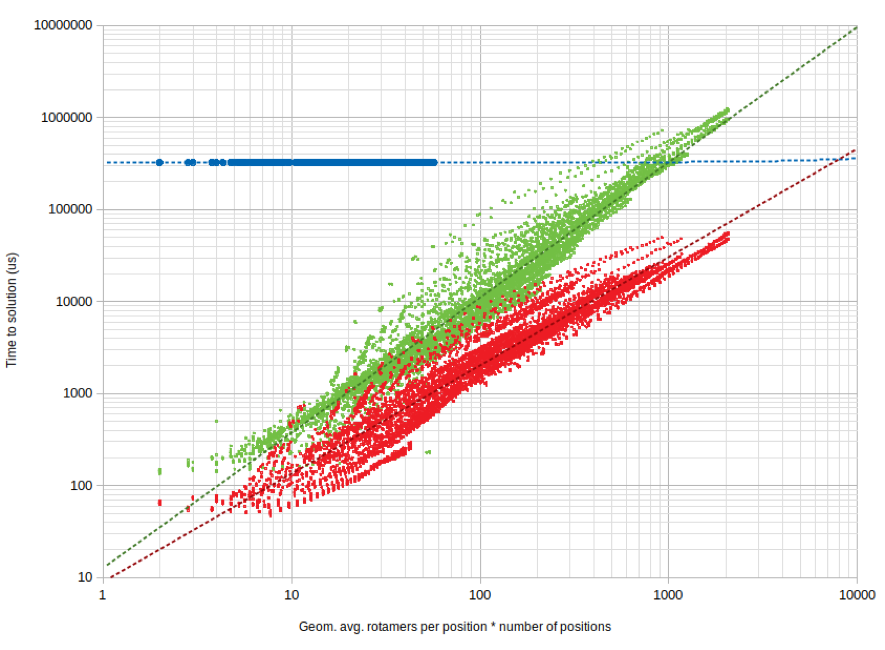
Time to solution for single-chip QPacker (blue), Toulbar2 (green), and Rosetta (red).

 

Annealing times remain constant for these small problems! But this behavior is for variables < 100, which is not enough to make a real conclusion from.

 

Question: how does time to solution scale asymptotically?

Our Work (Ongoing)

Refining scaling conclusions

Quantum annealing is not yet competitive with classical state-of-the-art solvers (cannot easily represent large problems). But QA hardware continues improve rapidly.

To make the argument that QA will be a better method once hardware improves, we need to show that our approach scales better than existing methods.

 

We will evaluate scaling on several metrics (energy difference from optimal solution, total annealing time, total iterations).

Our Work (Ongoing)

Improving algorithm for large problems

D-Wave provides an out-of-the-box hybrid solver called QBSolv. It is usable for 20-30 residue design problems, but scales poorly beyond that.

 

The largest proteins designed to date have about 200 residues.

 

Since QBSolv uses no domain-specific knowledge to solve CPD problems, we are modifying it to leverage certain assumptions and improve its scaling behavior.