Zero Knowledge Proofs
What are they?
A method where you can convince someone you know "something" without revealing what that thing is
eg. Location of some treasure, a Sudoku Solution, Where is Waldo
Knowledge Proof
Mathematical Proof
If \(n^2\) is even, then \(n\) is even
An argument showing that the stated assumptions logically guarantee the conclusion.
The treasure is buried at 43.44588, -80.50090
A process in which you prove to another party that you know "something"
vs.
How could this even be possible?

❓
✅
🤖




- Not modified
- Not tampered with
- No information revealed
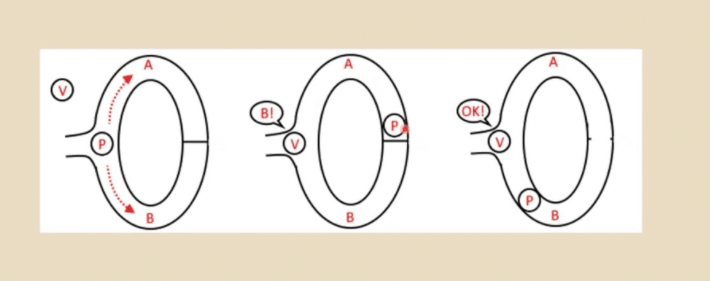
Alibaba's Cave
Make sense?
Why talk about them?
"Spooky Moon Math"

"Shouldn't be possible"
Two things we thought were true about ZKP
1. There is limited "types" of statements/problems you can construct a ZKP for. Not all information can be conveyed via a ZKP
2. The way you construct a ZKP for a type of information is unique and hard to discover.
Turns out both are false!
You can encode any information in a ZKP and there's a known process to do it!
Statement → Boolean Logic → CNF
Boolean Encoding ← 3SAT ← 3CNF
3 Coloring Problem → 3Color ZKP → Polynomial Encoding
QAP ← R1CS ← Arithmetic Circuit
zk-SNARK
3 Coloring Problems
❌
✅
At any point if I reveal two nodes of the same color I know you are full of shit
So how can we make a statement into a 3 color problem?
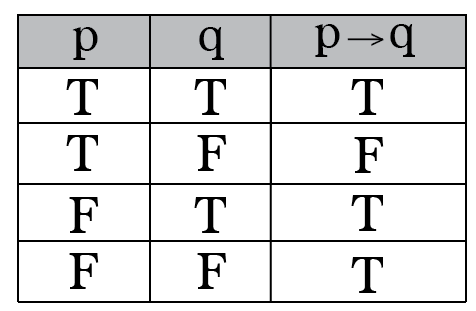
If it's raining and it's not freezing, plants will grow
I know this is super simple, but the complexity scales up pretty quick
Define our "literals" (things that are either true or false)
"raining" AND NOT "freezing" → "growth"
FRG + FRG +FRG +FRG +FRG
True
False
Neutral
A
B
A or B
True
False
Neutral
A
B
A or B
True
False
Neutral
A
B
A or B
True
False
Neutral
A
B
A or B
True
False
Neutral
A
B
A or B
True
False
Neutral
A
B
A or B
Put it all together
- Convert your info into boolean logic
- Re-arrange the logic in 3CNF form
- Change it into a 3 color map
- Execute your ZKP