Knowledge Graph Embeddings

Outline

• Why embed the KG ?
• Notations
• General Algorithm
• Scoring Function
  • Translation Based
  • Semantic Matching Based
• KG embedding with additional resources
  • Entity types
  • Relation Paths
  • Textual Descriptions
• Conclusion

Outline

• Why embed the KG ?
• Notations
• General Algorithm
• Scoring Function
  • Translation Based
  • Semantic Matching Based
• KG embedding with additional resources
  • Entity types
  • Relation Paths
  • Textual Descriptions
• Conclusion

• Embedding the KG into a continuous space while preserving the properties and semantics of the whole KG.
• Applications
  • Link Prediction: 
  • Triple Classification:
  • Entity Resolution:
  • Relation Extraction:
  • Question Answering:

Why Embed the KG ?

Outline

• Why embed the KG ?
• Notations
• General Algorithm
• Scoring Function
  • Translation Based
  • Semantic Matching Based
• KG embedding with additional resources
  • Entity types
  • Relation Paths
  • Textual Descriptions
• Conclusion

Notations

• KG contains entities $e \in \mathbb{E}$ and relationships $r \in \mathbb{R}$
• Each KB triple (fact) is represented by $(h,r,t)$
• $h$: head entity, $t$: tail entity and $r$: relation
• Example:  (AlfredHitchcock, DirectorOf, Psycho)
• Scoring function $f_r(h, t)$ : measures the plausibility of the fact $(h,r,t)$

Outline

• Why embed the KG ?
• Notations
• General Algorithm
• Scoring Function
  • Translation Based
  • Semantic Matching Based
• KG embedding with additional resources
  • Entity types
  • Relation Paths
  • Textual Descriptions
• Conclusion

General Algorithm

Outline

• Why embed the KG ?
• Notations
• General Algorithm
• Scoring Function
  • Translation Based
  • Semantic Matching Based
• KG embedding with additional resources
  • Entity types
  • Relation Paths
  • Textual Descriptions
• Conclusion

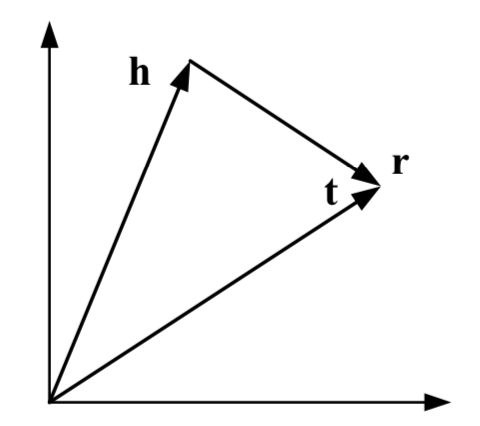
Translation Based Approaches - TransE

• Head entity $\mathbf{h}$ and tail entity $\mathbf{t}$ of a fact $(h,r,t)$ are vectors in $\mathbb{R}^d$
• Relation $\mathbf{r}$ is a translation in $\mathbb{R}^d$
• Scoring function: $f_r(h,t) = -\lVert \mathbf{h}+\mathbf{r}-\mathbf{t}\lVert_{1/2}$  
• Ranking Loss: $\mathcal{L} =$