Resource Verification of Lazy Evaluation and Memoization

- Ravichandhran Madhavan, Sumith Kulal, Viktor Kuncak

11th February, 2017

Static Analysis

  • Analysing the program without executing it

Why do you need it?

To find *hidden* bugswhich might get revealed only after months into production

Dev tools ftw

Motivation

Consider an example:

Side channel attacks

Image credits: https://www.tau.ac.il/~tromer/acoustic/img/nobody-listens3.jpg

A timing attack watches data movement into and out of the CPU or memory on the hardware running the cryptosystem or algorithm.

Motivation

  • Embedded systems - One wants to use hardware that is just good enough to accomplish a task in order to produce a large number of units at lowest possible cost.
  • Hard real-time systems - One needs to guarantee specific worst-case running times to ensure the safety of the system. [1]
[1]: Multivariate amortized resource analysis, ACM TOPLAS 2012

Introduction

We propose a system for specifying and verifying resource bounds

  • For functional programs that use recursive data-structures
  • Meant for verifying precise bounds

Specifying Resource Bounds

Natural to specify as templates : expressions with numerical holes

traverse(t: Tree): Int = {
     …
} ensuring(time <= a*size(t)+b &&
        parallel-time <= a*height(t)+b)
  • a and b are numerical holes
  • size and height are recursive functions

Resource Verification Problem

Specifying Resource Bounds

The Problem

 

  1. The values yield a valid bound for the resource
  2. The bound is as strong as possible for the given template

Infer values for the numerical holes such that

Our Tool

Orb

Big O

resource

bounds

Contributions

 

  • Recursive functions
  • Algebraic data-types
  • Nonlinearity

A system for solving resource bound templates

Implementation and application to sequential and parallel execution time bounds

An algorithm for solving ∃∀ formulas with

Crux is the instrumentation

traverse(t: Tree): Int = {
     body
} ensuring(time <= a*size(t)+b)
traverse(t: Tree): (Int, Int) = {
     (body, resource-usage)
} ensuring(res._2 <=a*size(t)+b)

Instrumentation

Verification Condition (VC) Generation

f(x) = {
  require(pre)
     body
} ensuring(post)

∀x. ϕpre ∧ ϕbody ⟹ ϕpost

VCs with free variables

traverse(t: Tree) = {
   …
} ensuring(res._2 <= a*size(t)+b))

Postconditions contain numerical holes
They become free variables in the VCs

 

Goal: Solve for free variables in VCs

Orb algorithm

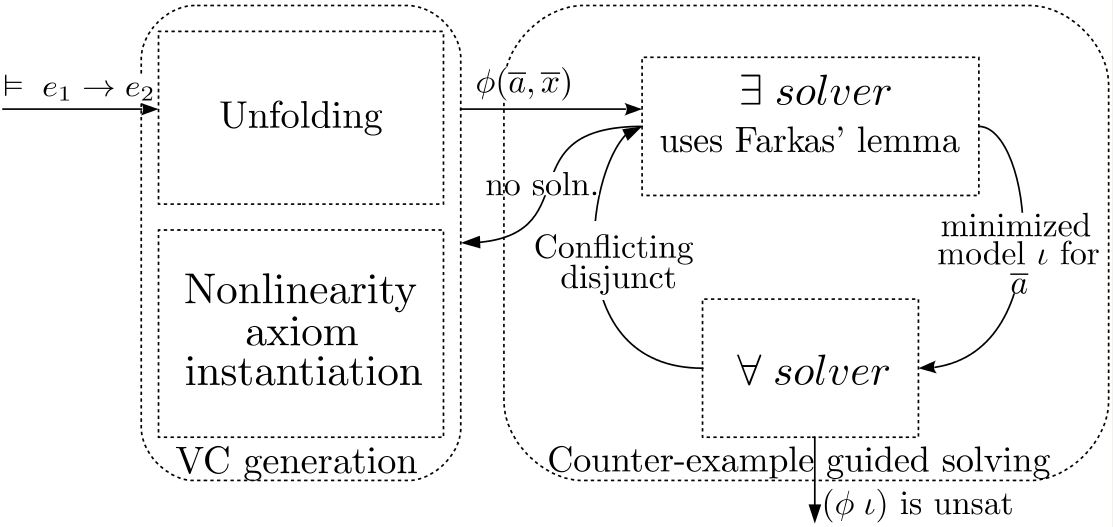
[R. Madhavan & V. Kuncak, CAV ’14]

Bounds Inferred by the Tool

Benchmark Bound inferred
AVL tree 145*height(t) + 19
Red-Black tree 178*blackHeight(t) + 96
Binomial heap - deleteMin 70*treenum(h1) + 31*minchildren(h2) + 22
Leftist heap - merge 22*rheight(h1) + 22*rheight(h2) + 1
Insertion sort 8 * size(l) * size(l) + 2

Wall clock time vs. steps

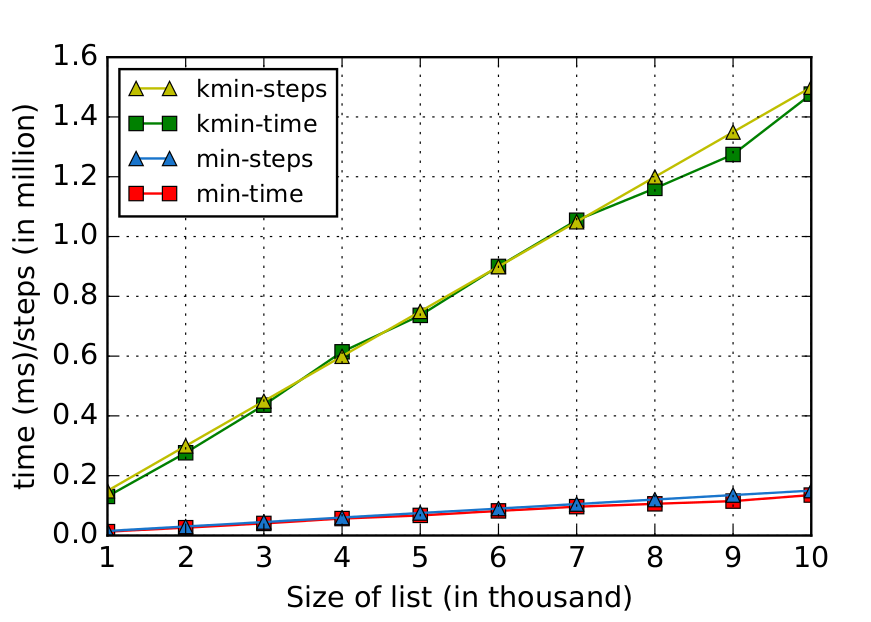
Lazy evaluation and memoization

The problem...

The problem...

The model

Representing Suspensions as ADTs: For every type () => B in the source program we create an ADT denoted LazyB. For functions f1, f2.. that return B, constructors C1, C2.. are added

Cache encoding. We instrument the expressions of the source

program to explicitly track the changes to the cache as the pro-

gram undergoes evaluation.

Experimental evaluation

  • Compared the Orb obtained results with instrumented code.

     
  • Reasons of inaccuracy :
  1.  Forcing to a template.
  2.  Inaccuracy due to the tool.

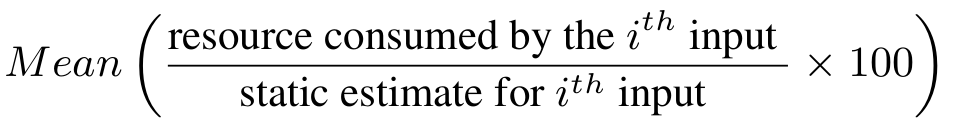
Runtime Vs. Static estimates

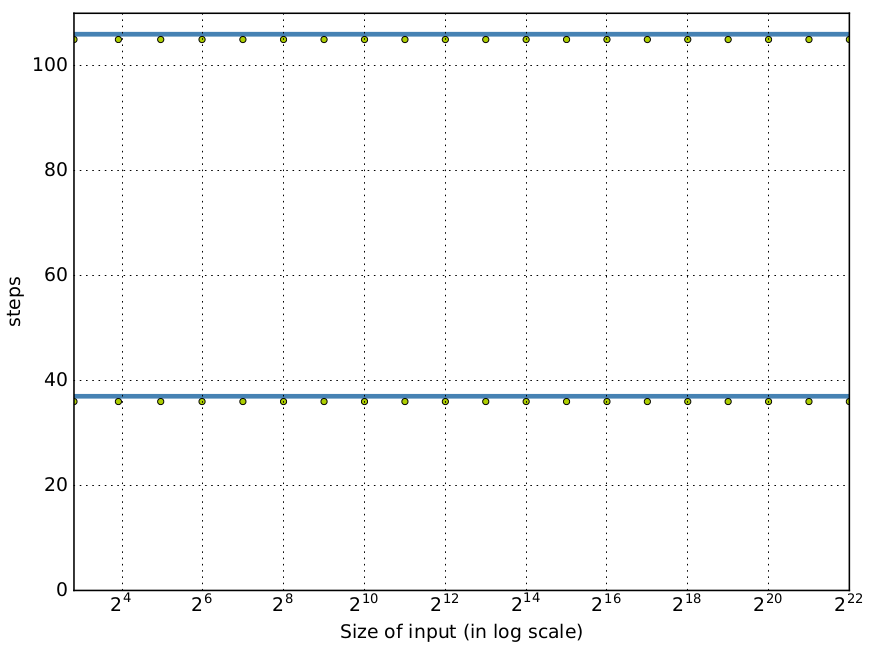
lazy numerical rep.
real time queue

Runtime Vs. Static estimates

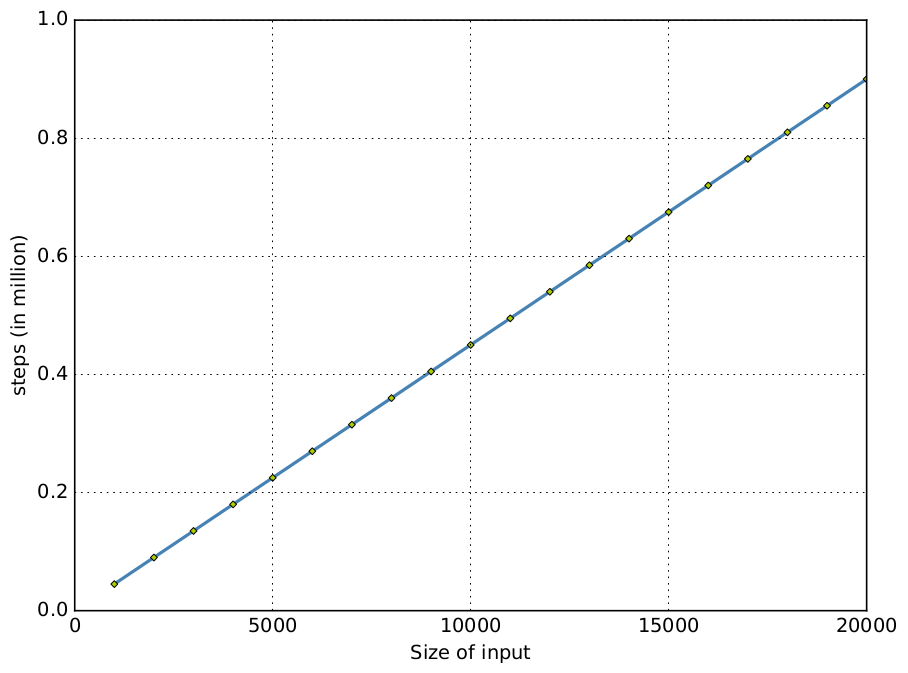
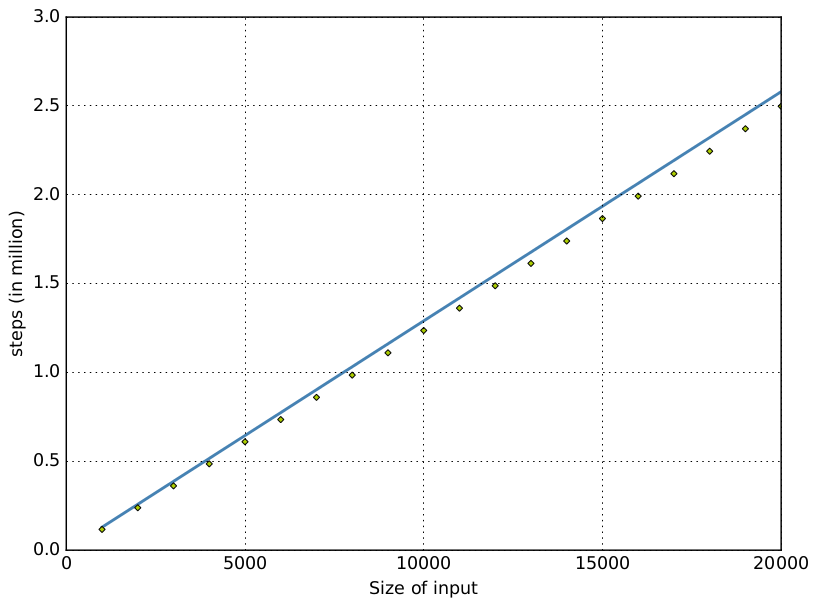
Cyclic Fibonacci Stream
Cyclic Hamming Stream

Runtime Vs. Static estimates

Levenshtein Distance

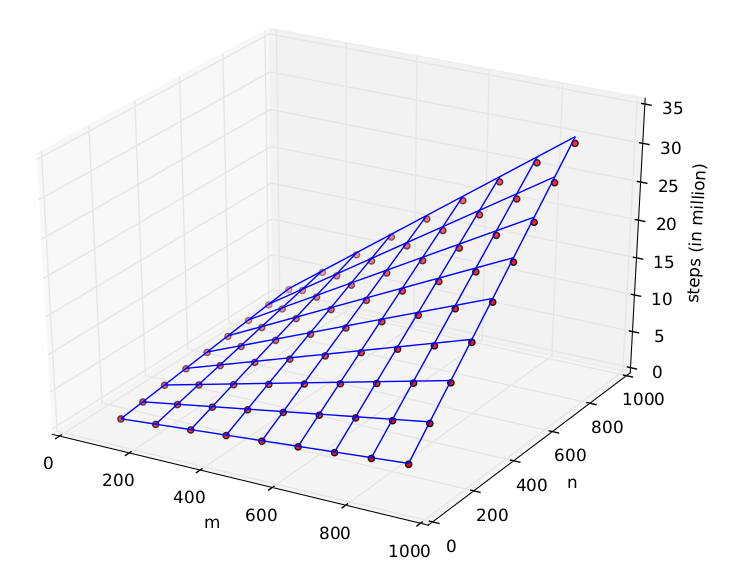
Runtime Vs. Static estimates

Lazy Bottom-up merge sort - O(k*log(l.size) + l.size)

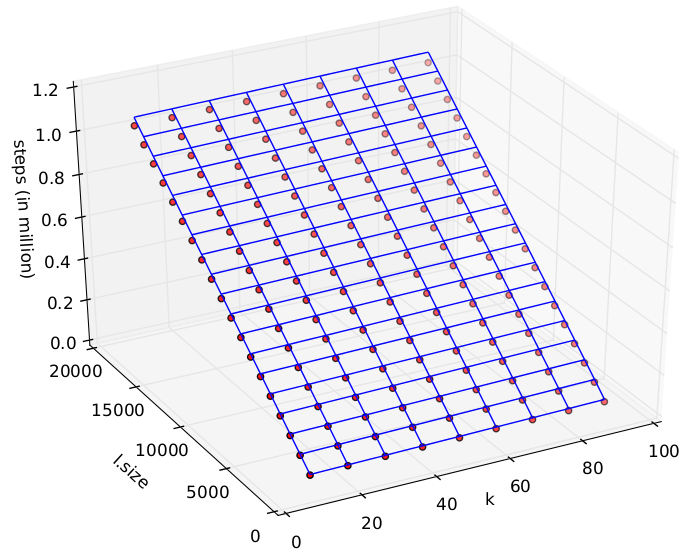
Template Minimization

Orb infereed formula: 129*n + 4

Least value of coeff 0 is 4.
The formula that goes through is 129*n + 4.
Counter-example for 129*n + 3 is at the point 0

Least value of coeff 1 is 124.
The formula that goes through is 124*n + 4.
Counter-example for 123*n + 4 is at the point 8000

Minimization report ends here

Report for Cyclic Fibs.

Formula :- a*x + b

subject to a set of inputs

1. a*x + c
2. d*x + b

Compare 1. and 2. with dynamic count.

Bar graph highlighting % accuracy

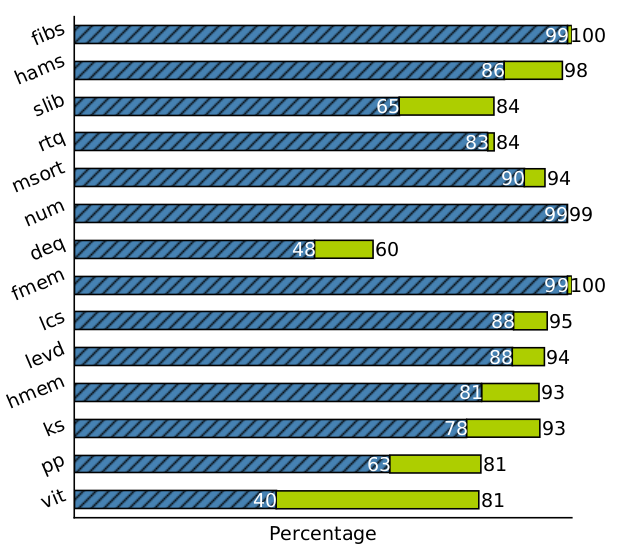
Why the inaccuracy?

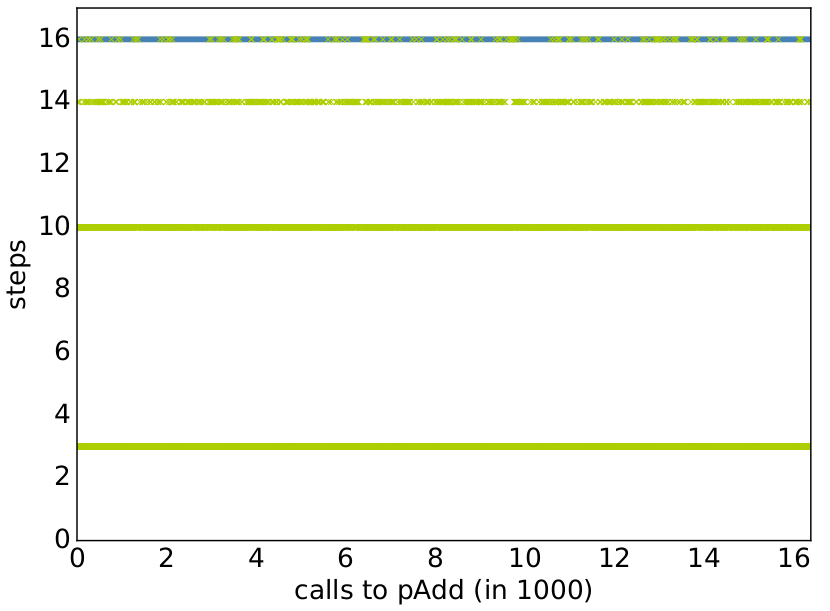
The intermediate functions are indeed accurate

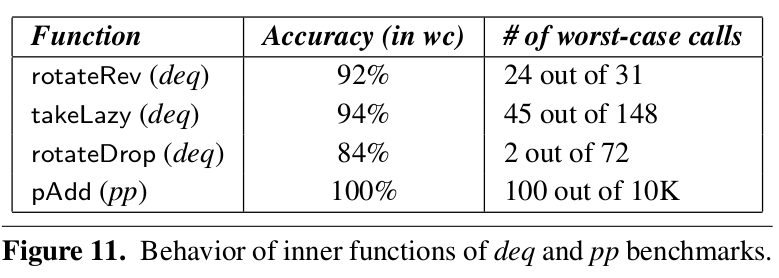
More in the paper

Conclusions and related works.

  • Lazy evaluation and memoization successfully modelled with good results on real life case studies.
  • Related works:

    Towards Automatic Resource Bound Analysis for OCaml.
    Jan Hoffmann, Ankush Das, and Shu-Chun Weng.
    Type-based allocation analysis for co-recursion in lazy functional languages.  Vasconcelos, Pedro Baltazar; Jost, Steffen; Florido, Mario; Hammond, Kevin.
    Analysing the Complexity of Functional Programs: Higher-Order Meets First-Order. Martin Avanzini, Ugo Dal Lago, Georg Moser

Hope you enjoyed!

GitHub: Sumith1896

Twitter: @sumith1896

Email: sumith1896@gmail.com

Thank you and get in touch :)

"Essentially, all models are wrong, but some are useful."

                                              - George E. P. Box

Catch me at

Made with Slides.com