Lazy evaluation

alive or dead example!

A space leak can occur when the memory contains an expression—where the expression grows regularly but where the evaluated value would not grow. Forcing evaluation usually solves such leaks; this makes evaluation of some variables strict instead of lazy.

f x y = y


f ⊥ b = b

f ⊥ b = ⊥

Lazy Evaluator

Postpone evaluation until it is inevitable.

Lazy evaluation in a nutshell

• takes two args of any type
• evaluates first
• returns the second
• superficial dependency 

seq :: a -> b -> b

seq ⊥ b = ⊥
seq a b = b

seq2 x y = if (x == 0) then y else y

Declares a function to be strict in an argument.

f !x y = x + y

• strict in first argument
• not strict in second argument
• x evaluated to WHNF
• syntactic sugar for seq

Bang Patterns

Examples

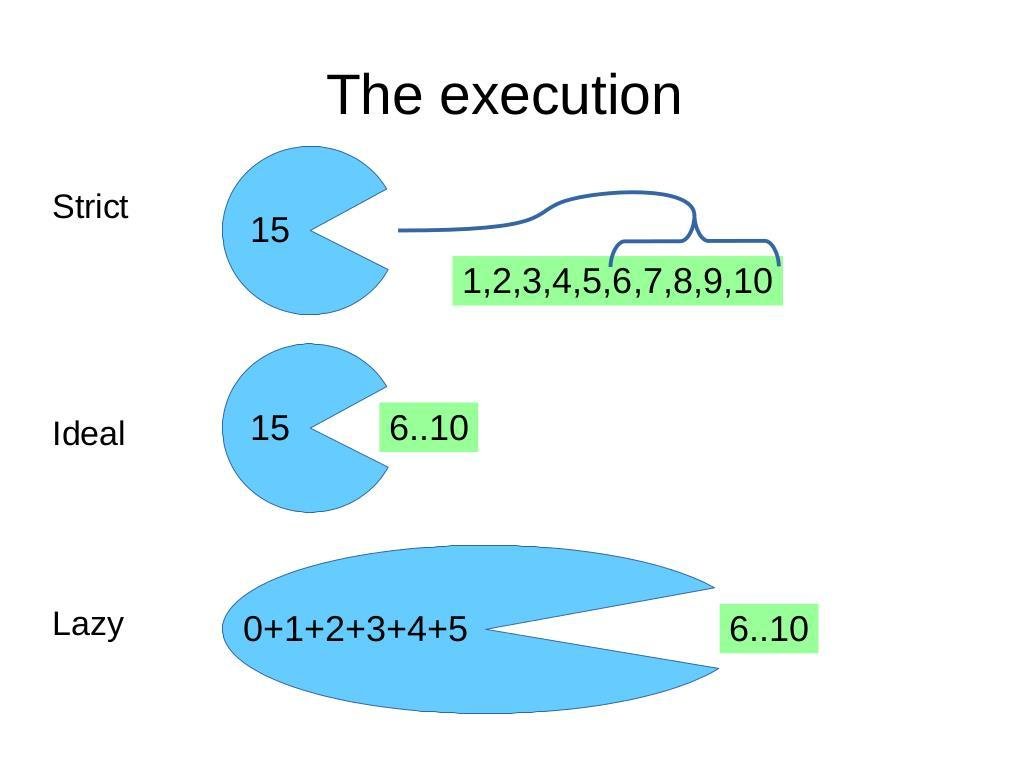
Strictness based

foldl vs foldl'

foldl f z []     = z
foldl f z (x:xs) = foldl f (f z x) xs

foldl (+) 0 [1..10]
= foldl (+) 0 (1:[2..10])
= foldl (+) (0 + 1) [2..10]
= foldl (+) ((((((((((0 + 1) + 2) + 3) + 4) + 5) + 6) + 7) + 8) + 9) + 10) []        
= ((((((((((0 + 1) + 2) + 3) + 4) + 5) + 6) + 7) + 8) + 9) + 10)
= (45 + 10)
= 55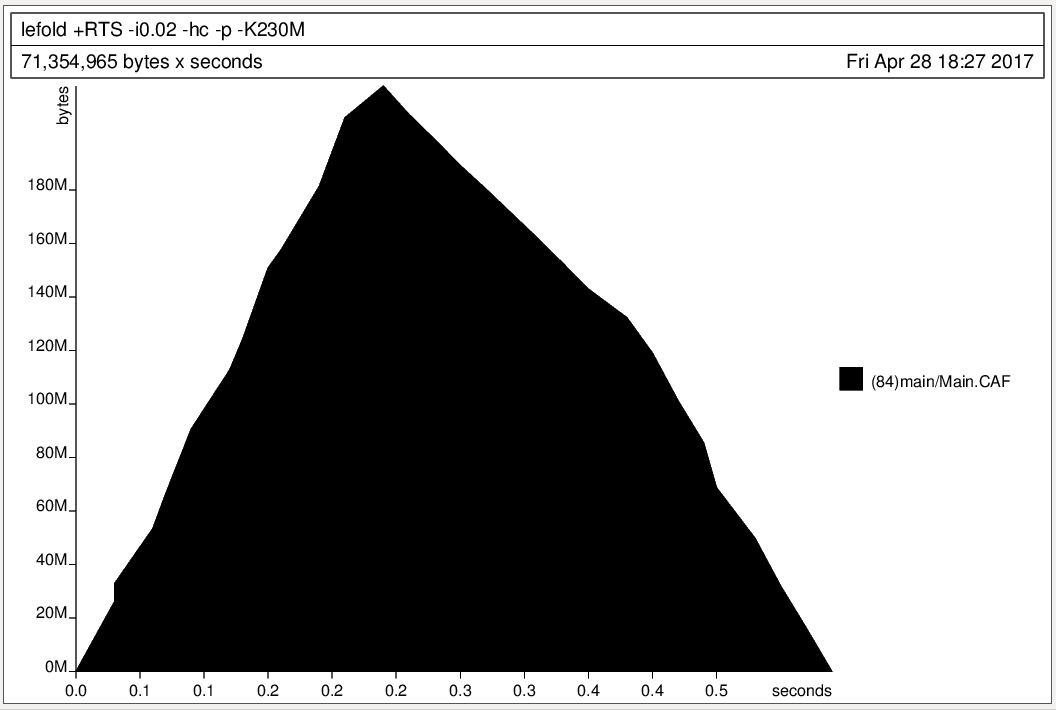

foldl vs foldl'

foldl' f z []     = z
foldl' f z (x:xs) = let z' = z `f` x 
                     in seq z' $ foldl' f z' xs

foldl' (+) 0 [1..10]
= foldl' (+) 0 (1:[2..10])
= foldl' (+) (0 + 1) [2..10]
= foldl' (+) 1 (2:[3..10])
= foldl' (+) (1 + 2) [3..10]
...
= foldl' (+) (45 + 10) []
= foldl' (+) 55 []
= 55

tick

main = print (f ([1..40000000]}) 
                (0 :: Int, 1 :: Int))

f [] c =  c
f (x:xs) c = f xs (tick x c)

tick x (c0, c1) = if (even x) 
                    then (c0, c1 + 1) 
	            else (c0 + 1, c1)

f [1,2,3,4] (0,1)
= f [2,3,4] (tick 1 (0,1))
= f [3,4] (tick 2 (tick 1 (0,1)))
= f [4] (tick 3 (tick 2 (tick 1 (0,1))))
= f [] (tick 4 (tick 3 (tick 2 (tick 1 (0,1)))))
... 
= (tick 4 (tick 3 (tick 2 (tick 1 (0,1)))))
= (tick 4 (tick 3 (tick 2 ((0 + 1),1))))
= (tick 4 (tick 3 ((0 + 1),(1 + 1))))
= (tick 4 (((0 + 1) + 1),(1 + 1)))
= (((0 + 1) + 1),((1 + 1) + 1))
= ((1 + 1),(2 + 1))
= (2,3)

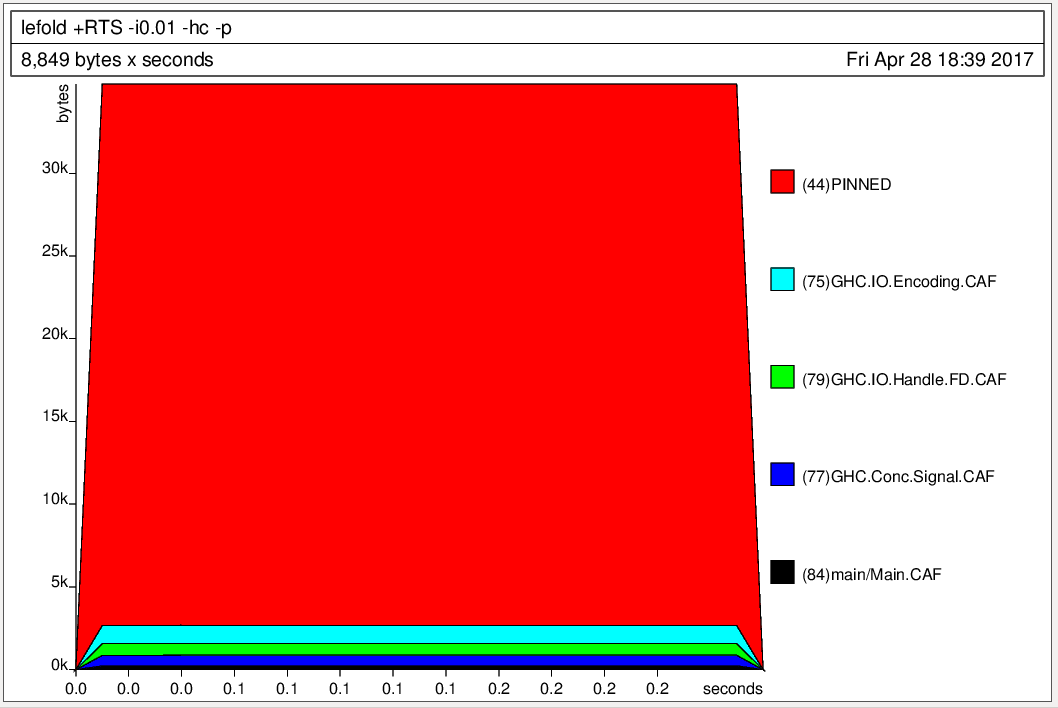
tick

main = print (f ([1..40000000]}) 
                (0 :: Int, 1 :: Int))

f [] !c =  c
f (x:xs) !c = f xs (tick x c)

tick x (!c0, !c1) = if (even x) 
                    then (c0, c1 + 1) 
	            else (c0 + 1, c1)

f [1,2,3,4] (0,1)
= f [2,3,4] (tick 1 (0,1))
= f [2,3,4] (0+1, 1)
= f [2,3,4] (1, 1)
= f [3,4] (1, 1+1)
= f [3,4] (1, 2)
= f [4] (1+1, 2)
= f [4] (2, 2)
= f [] (2, 2+1)
= f [] (2, 3)
= (2, 3)

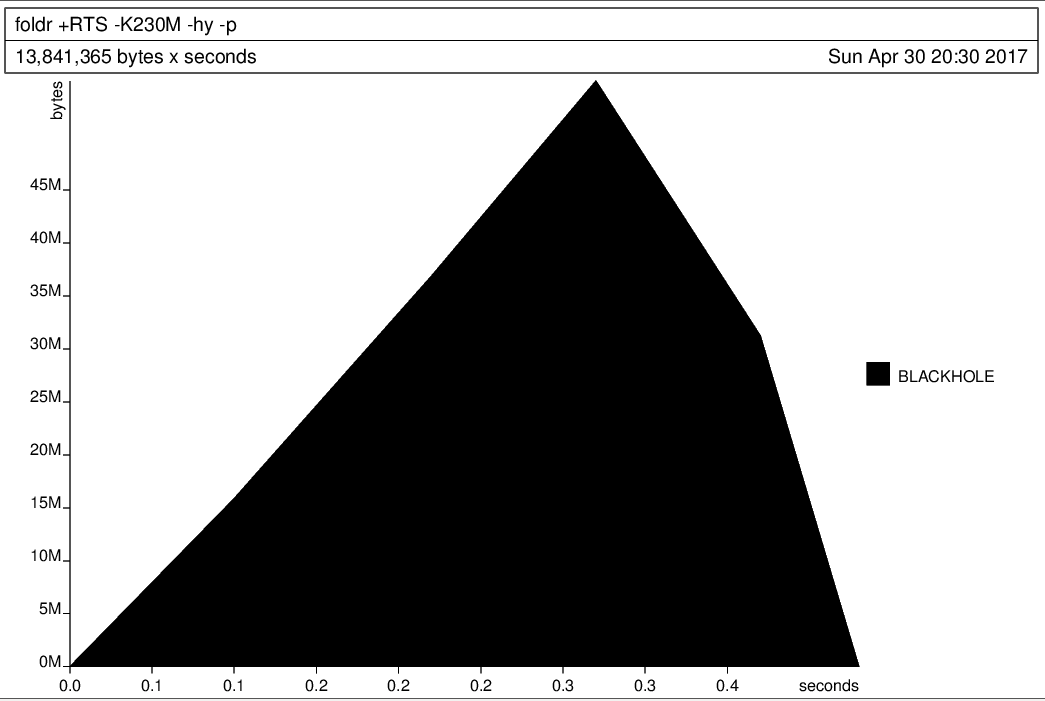
foldr

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f z []     = z 
foldr f z (x:xs) = f x (foldr f z xs)

foldr (+) 0 [1..4]
= 1 + (foldr (+) 0 [2..4])
= 1 + (2 + (foldr (+) 0 [3..4]))
= 1 + (2 + (3 + (foldr (+) 0 [4])))
= 1 + (2 + (3 + (0 + 4)))
...
= 10

Examples

Liveness based - with fixes

surprise!

surprise :: String -> String
surprise s = let b = break (== '\n') s
                in (fst b) + "\nsurprise\n" + (snd b)

break :: (a -> Bool) -> [a] -> ([a], [a])
break f [] = ([], [])
break f x:xs =  | x == xs     = ([], xs)
  | otherwise   = let b = break f xs in (x:(fst b), (snd b))

surprise "P not \nequal to NP"
= (fst b1) + "\nsurprise\n" + (snd b1)
  where b1 = break (!= '\n') "P not \nequal to NP"
= 'P' + ((fst b1) + "\nsurprise\n" + (snd b1))
  where b1 = ('P':(fst b2), snd b2)
        b2 = break (!= '\n') " not \nequal to NP"
= 'P' + ' ' + ((fst b3) + "\nsurprise\n" + (snd b1))
  where b1 = ('P':(fst b2), snd b2)
        b2 = (' ':(fst b3), snd b3)
        b3 = break (!= '\n') "not \nequal to NP"

E (fst b) (snd b)
where b = (E1, E2)

E E1 E2

= 'P' + ' ' + ((fst b3) + "\nsurprise\n" + (snd b3))
  where b3 = break (!= '\n') "not \nequal to NP"

garbage

collection

surprise!

• Current GHC version have incorporated Wadler's ideas in the garbage collector
• Bug no longer reproducible

break ls = let (xs, ys) = (SYNCHLIST ls) 
           in (PAR before '\n' ls, PAR after '\n' ls)

Hughes' solution:

• careless use can lead to deadly issues
• time complexity not necessarily linear

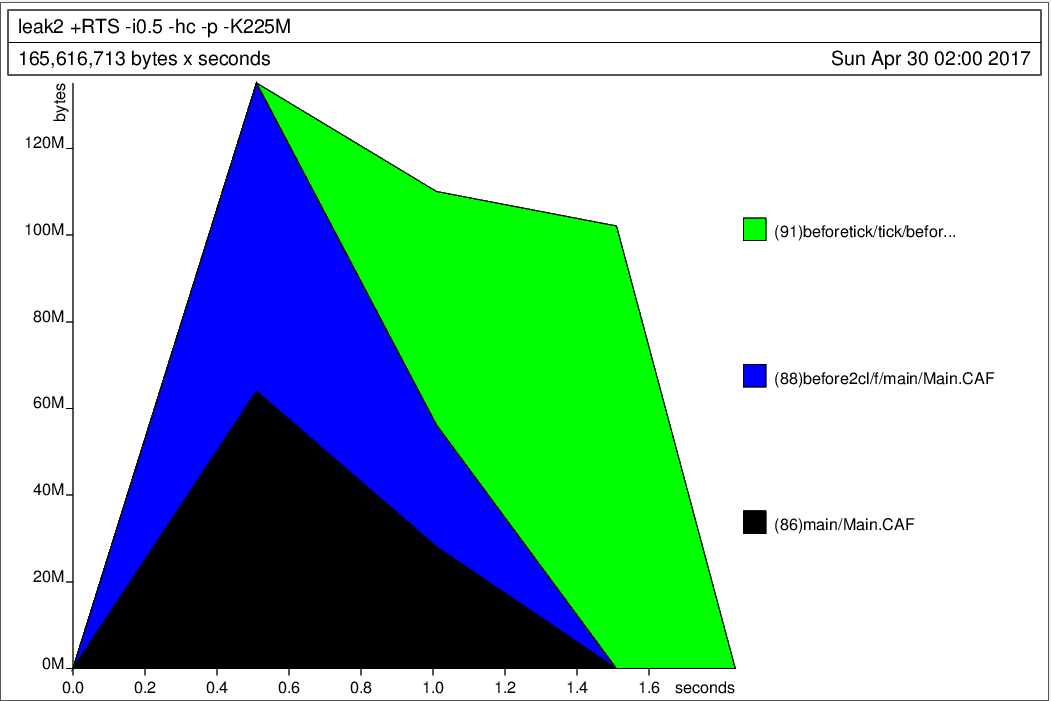
A hack

to detect space leaks

The Method

• Compile the program for profiling
• Run the executable with limiting the stack space
• Find the stack size for which the program just runs
• Reduce the stack space by small amount, run with -xc
• Identify the source of the leak, attempt to fix
• If fixed, should run with small stack space

main = do print (f [1..1000000])

f [] = 0
f x = 1 + g x

g [] = 0
g x = h (tail x)

h [] = 1
h x = foldl (+) 0 x

Flaws with this hack

• Adjacent duplicates are ignored
• Not all functions for imported libraries
• High stack space doesn't mean space leak
• Last function may not be the culprit!