Item-Based Collaborative Filtering Recommendation Algorithms
matthew sun · mdsun@princeton.edu
citp recsys reading group · 1/12/21
📸 big picture
- state-of-the-art for recommendation was user-based k-nearest neighbors (KNN) approaches
- main drawback: issues at scale
- main thrust of paper: item-based recommendation algorithms yield as good/better error rates at much higher throughput
- 💡 I was intrigued to see the emphasis on performance; many modern machine learning papers focus on achieving SOTA on a particular accuracy metric
📃 introduction
- "collaborative filtering"
- works by building a database of preferences for items by users
- new user Neo matched against database to discover neighbors
- items liked by Neo's neighbors are recommended to Neo
- two main challenges: scalability & quality
- search tens of millions of neighbors; also, there may be lots of information about every individual user
📃 introduction (cont)
- item-based algorithms
- explore relationships between items rather than relationships between users
- avoid bottleneck of having to search database of users for similar users
- cold start problem?
- "because relationships between items are relatively static, item-based algorithms may be able to provide the same quality as user-based algorithms"
- assumes that the measure of item similarity accurately captures something about user preferences
🌐 overview of collaborative filtering
- ❗ interesting tidbit: this paper (like many older RS papers) assumes the setting of e-commerce
- collaborative filtering overview:
\mathcal{U} = {u_1, u_2,\cdots,u_m} \\
\mathcal{I} = {i_1, i_2,\cdots, i_n}
u_i
I_{u_i} = \{\cdots\}
(items the user has "expressed opinions about" - i.e., rated, purchased, liked, etc.)
🌐 overview of collaborative filtering
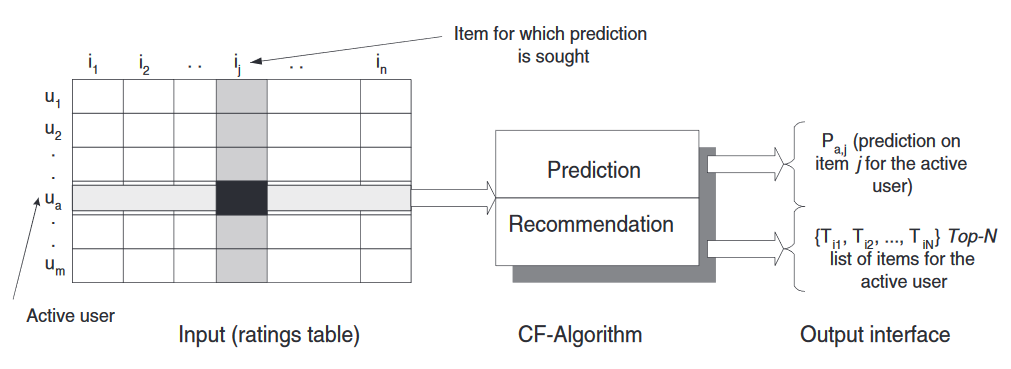
🌐 overview of collaborative filtering
- two distinct tasks
- prediction
- predicted "opinion value" of user for item
- recommendation
- list of N items that the active user will like the most (also known as Top-N recommendation)
- prediction
- memory (user-based) vs model (item-based)
- item-based: develop model of user ratings, conditional on interaction with other items
i_j
u_i
🎁 item-based methods
- problem set up: target user and target item
- select k most similar items:
- compute similarity of each item to the target item
u_a
i
\{i_1, i_2,\cdots, i_k\} \subseteq I_{u_a}
\{s_{i_1}, s_{i_2},\cdots, s_{i_k}\}
🎁 item-based methods
- problem set up: target user and target item
- select k most similar items:
- compute similarity of each item to the target item
- produce prediction by computing weighted average of target user's ratings on similar items
u_a
i
\{i_1, i_2,\cdots, i_k\} \subseteq I_{u_a}
\{s_{i_1}, s_{i_2},\cdots, s_{i_k}\}
PREDICTION COMPUTATION
🎁 item-based methods
- problem set up: target user and target item
- select k most similar items:
- compute similarity of each item to the target item
- produce prediction by computing weighted average of target user's ratings on similar items
u_a
i
\{i_1, i_2,\cdots, i_k\} \subseteq I_{u_a}
\{s_{i_1}, s_{i_2},\cdots, s_{i_k}\}
\hat{R_{i}}
PREDICTION COMPUTATION
🎁 item-based methods
- problem set up: target user and target item
- select k most similar items:
- compute similarity of each item to the target item
- produce prediction by computing weighted average of target user's ratings on similar items
u_a
i
\hat{R_{i}}
PREDICTION COMPUTATION
🔩 types of similarity computation
cosine similarity
correlation-based similarity
adjusted cosine similarity
\text{cos}(\vec{i},\vec{j})=
\frac{\vec{i}\cdot\vec{j}}{\|\vec{i}\|_2 \|\vec{j}\|_2}
\frac{\sum_{u\in U}(R_{u,i}-\bar{R_i})(R_{u,j}-\bar{R_j})}{\sqrt{\sum_{u\in U}(R_{u,i}-\bar{R_i})^2} \sqrt{\sum_{u\in U}(R_{u,j}-\bar{R_j})^2}}
(Pearson correlation)
U
defined as set of all users who rated both items
\frac{\sum_{u\in U}(R_{u,i}-\bar{R_u})(R_{u,j}-\bar{R_u})}{\sqrt{\sum_{u\in U}(R_{u,i}-\bar{R_u})^2} \sqrt{\sum_{u\in U}(R_{u,j}-\bar{R_u})^2}}
(basically, cosine similarity, but "standardize" each user by subtracting their mean rating)
🧪 prediction computation
weighted sum
adjusted cosine similarity
I_S:
set of all items determined to be similar to target item
P_{u,i}=\frac{\sum_{j\in I_S}(s_{i,j}\cdot R_{u,j})}{\sum_{j\in I_S}|s_{i,j}|}
P_{u,i}=\frac{\sum_{j\in I_S}(s_{i,j}\cdot R'_{u,j})}{\sum_{j\in I_S}|s_{i,j}|}
R'_N=\alpha R_i + \beta + \epsilon
📊 experimental evaluation
- Pre-compute similarity between items
- For each item, compute most similar items, where ( = model size)
- Might this suffer from issues of staleness?
- Data set: MovieLens
- 43k users, 3.5k movies
- Only consider users with 20+ movie ratings
- Might this bias the evaluation?
- Multiple different train/test splits
- Evaluation metric: MAE
k
k << n
k
\frac{\sum_{i=1}^N |p_i-q_i|}{N}
prediction/rating pair
p_i,q_i
📊 experimental evaluation
- 10-fold cross validation for every train/test split
- Compare item-based to Pearson nearest neighbor algorithm
- Performed comparisons of similarity computation, training/test ratio, and neighborhood size
- Adjusted cosine similarity resulted in lowest MAE
- Selected 80/20 training/test split
- Compared weighted sum to regression based approach
- Select 30 as optimal neighborhood size
📊 experimental evaluation (cont.)
- user-user vs item-item at various neighborhood sizes (80/20 training/test split)
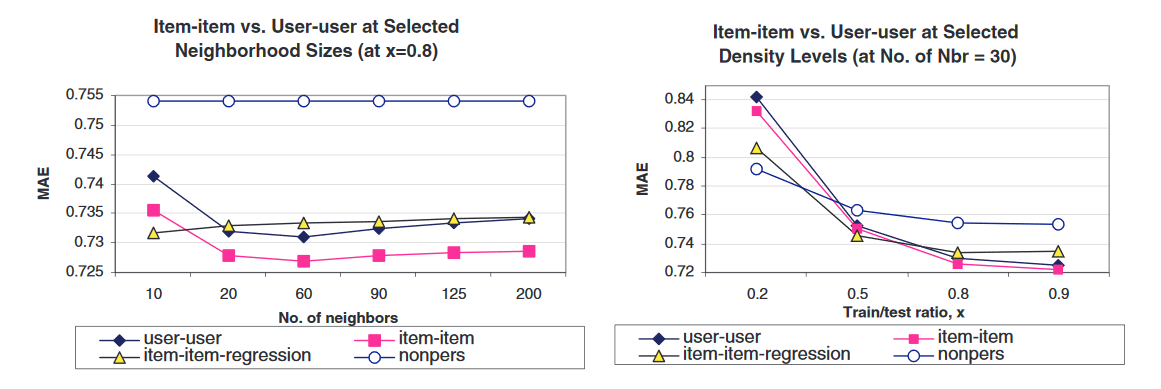
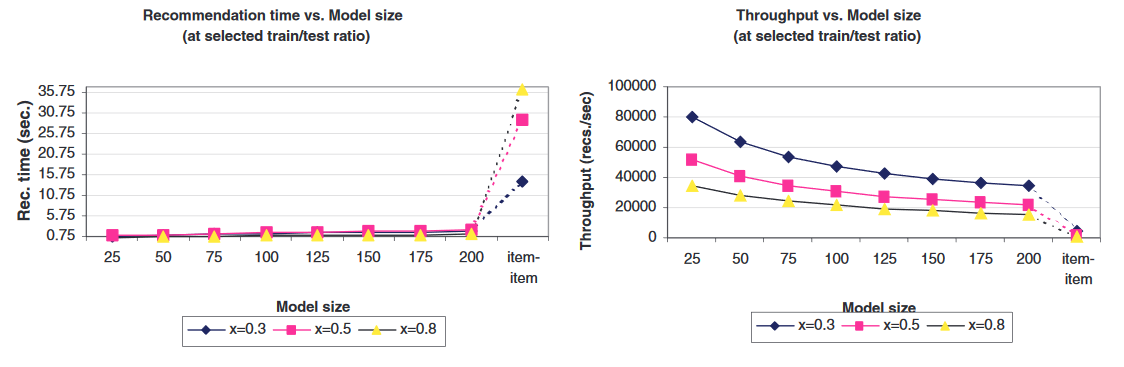
📊 experimental evaluation (cont.)
- Throughput decreases as training set size increases
- Recommendation time may be misleading (at smaller x, recommendations are made on more test cases)
💬 discussion
- item-item provides better quality predictions ("however, the improvement is not significantly large")
- as measured by MAE
- when do differences in MAE stop providing useful signal?
- only for users with 20+ movie ratings
- as measured by MAE
- "...the item neighborhood is fairly static...which results in very high online performance"
- no runtime comparison to user-user system