Suyash Bagad

Department of Electrical Engineering, IIT Bombay

As a Part of Dual Degree (B.Tech + M.Tech) Project

Prof. Saravanan Vijayakumaran

Guide

June 29, 2020

Shorter, Privacy-Enhancing

Proof of Reserves 

Proof of Reserves 

Outline

Log-sized Privacy-Enhancing Proofs of Reserves Protocol

Motivation and main idea

Confidentiality of Amounts in Grin

Presented at Crypto Valley Conference on Blockchain Technology, 2020

Focus on performance trade-offs and implementation

Work accepted at IEEE Security & Privacy on Blockchain, 2020

Graph-based analysis of the Grin Blockchain

Main challenge in design

Adaptability to Edwards and Ristretto curves

MimbleWimble

Monero

Revelio

\mathcal{C}_{\text{own}}
C = g^{k} \cdot h^{a}
C \in \mathcal{C}_{\text{own}} \implies k \text{ is known}

Each output in MimbleWimble is a Pedersen Commitment

For an amount \(a \in \{0,1,\dots,2^{64}-1\}\) and blinding factor \(k \in \mathbb{Z}_q\)

where \(g,h \in \mathbb{G}\) such that DL relation between them is unknown

Revelio

\mathcal{C}_{\text{anon}}
1
2
3
4
5
6
7
8
9
10
12
11
13

For each \(C_i \in \mathcal{C}_{\text{anon}},\) publish the tags \((I_1, \dots, I_n) \in \mathbb{G}^n\) where \( n = |\mathcal{C}_{\text{anon}}|\)

Publish \(C_{\text{assets}} = \prod_{i \in [n]} I_i,\) and NIZK proofs \(\sigma_i \in \mathbb{Z}_q^5  \ \forall i \in [n]\)

PoK\big\{\underbrace{(\alpha,\beta,\gamma)}_{\text{secret}} \ | \ \underbrace{(C_i = g^{\alpha} \cdot h^{\beta} \ \wedge \ I_i = g_t^{\alpha} \cdot h^{\beta}) \vee (I_i = g_t^{\gamma}) }_{\text{statement}} \big\}

where \(y_i = \mathcal{H}(k_{\text{exch}}, C_i) \in \Z_q\)

I_i = \begin{cases} \ g_1^{k_i} \cdot h^{a_i} & \text{if } C_i \in \mathcal{C}_{\text{own}},\\ \ g_1^{y_i} & \text{if } C_i \notin \mathcal{C}_{\text{own}}, \end{cases}

Drawbacks of Revelio

Proof size linear in anonymity set size

(n+1) \text{ in } \mathbb{G}, \ 5n \text{ in } \mathbb{Z}_q

Can we shrink proofs sizes to \(\mathcal{O}( \text{log}_2(n))\)? 

Can we link the blockchain state to the proof of reserves?

Privacy of outputs depends on the anonymity set \(n\)

RevelioBP!

RevelioBP!

1
2
3
4
5
6
7
8
9
10
12
11
13
0
1
0
0
0
0
0
0
0
0
0
0
0
(
)
\textbf{e}_1 =
0
0
0
0
0
1
0
0
0
0
0
0
0
(
)
\textbf{e}_2 =
0
0
0
0
0
0
0
0
1
0
0
0
0
(
)
\textbf{e}_3 =
0
0
0
0
0
0
0
0
0
1
0
0
0
(
)
\textbf{e}_4 =
0
0
0
0
0
0
0
0
0
0
0
0
1
(
)
\textbf{e}_5 =
k_1
k_2
k_3
k_4
k_5
(
)
\textbf{k} =
PoK\left\{ \ (\textbf{k} \in \mathbb{Z}_q^s, \ \textbf{E} \in \mathbb{Z}_2^{s \times n}) \ | \ \textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j} \ \wedge \ \ I_j = g_t^{k_j}h^{a_j} \ \forall j \in [s] \ \right\}

Publish tag vector \((I_1, I_2, \dots, I_s),\) \(C_{\text{assets}} = \prod_{i \in [n]} I_i\) and NIZK \(\Pi_{\text{RevBP}}\)

More on RevelioBP

PoK\left\{ \ (\textbf{k} \in \mathbb{Z}_q^s, \ \textbf{E} \in \mathbb{Z}_2^{s \times n}) \ | \ \textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j} \ \wedge \ \ I_j = g_t^{k_j}h^{a_j} \ \forall j \in [s] \ \right\}

To build \(\Pi_{\text{RevBP}},\) we combine the constraints using a scalar \(u \leftarrow \mathbb{Z}_q\)

\prod_{j \in [s]} \left(g^{-k_j} \cdot g_t^{k_j} \cdot \textbf{C}^{\textbf{e}_{i_j}} \cdot I_j^{-1}\right)^{u^{j-1}} = 1,
\implies g^{- \langle \textbf{u}^s, \textbf{k} \rangle} \cdot g_t^{\langle \textbf{u}^s, \textbf{k} \rangle} \cdot \textbf{C}^{ \textbf{u}^s \textbf{E}} \cdot \textbf{I}^{- \textbf{u}^s} = 1,

We then use Inner Product Argument of the form 

PoK \left\{ (\textbf{a}, \textbf{b}) \in \mathbb{Z}_q^N \ | \ P = u^{c}\textbf{g}^{\textbf{a}} \textbf{h}^{\textbf{b}} \wedge c = \langle \textbf{a}, \textbf{b} \rangle \ \right\}
s + 2 \text{log}_2(sn+n+s+3) \text{ in } \mathbb{G}, \ 5 \text{ in } \mathbb{Z}_q
RevelioBP proof size Revelio proof size
(n+1) \text{ in } \mathbb{G}, \ 5n \text{ in } \mathbb{Z}_q

Performance Trade-offs

RevelioBP Revelio
Proof size
Scalability
Blockchain state
Output privacy
Inflation resistance
Own set size
Running times
\mathcal{O}(n)
\mathcal{O}(s+\text{log}_2(sn))
\mathcal{O}(sn)
\mathcal{O}(n)

For UTXO set size \(n=1.6\times 10^5\) and \(s=10^2\)

5\text{KB}
32\text{MB}
(164,68)\\[-3pt] \text{min}
(34,34)\\[-3pt] \text{min}

Proof Sizes

We implemented RevelioBP in Rust over \( \mathbb{G} = \texttt{secp256k1}\) elliptic curve

n \ \longrightarrow
s \ \longrightarrow
s=20
n=1000
\text{Proof size in KB} \longrightarrow

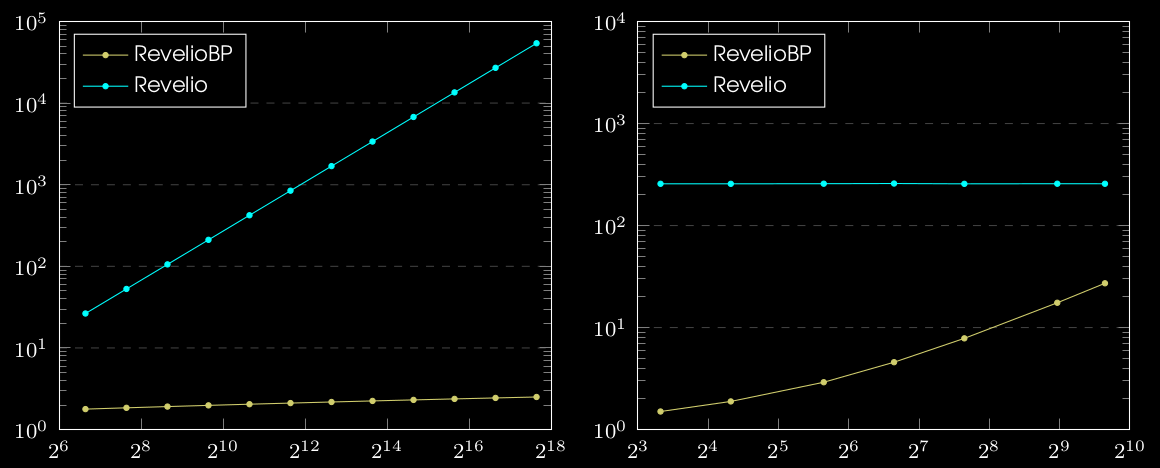
Note: All plots are in log-log scale.

RevelioBP proofs are \(\ge 10X\) shorter that that of Revelio

Running Times

RevelioBP proof generation is \(\approx 2X\) slower that of Revelio

n \ \longrightarrow
s \ \longrightarrow
s=20
n=1000
\text{Running time in mins} \longrightarrow

Note: All plots are in log-log scale.

RevelioBP ver. is \(\approx 3X\) faster than its gen. due to multi-exponentiation

MProve+

Key challenge: Unlinking key-images & one-time addresses in MProve

\Pi_{t_1} = \left\{ (P_1, I_1,\alpha_1, \beta_1), \ (P_2, I_2,\alpha_2, \beta_2), \ \ldots \ , \ (P_n, I_n,\alpha_n, \beta_n), \right\}
\textsf{Tx}_{t_2} = \{\mathcal{R}, I_{2}\}

Use an approach similar to RevelioBP

PoK\left\{ (\textbf{x}, \textbf{k} \in \mathbb{Z}_q^s, \ \textbf{E} \in \mathbb{Z}_2^{s \times n}) \ \bigg| \ \textbf{P}^{\textbf{e}_j} = g^{x_j}, \ \textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j}, \ \ I_j = g_t^{k_j}h^{a_j} \ \forall j \in [s] \ \right\}

An MProve+ proof looks like

\Pi^{+}_{t_1} = \{ \textbf{P}, \textbf{C}\in \mathbb{G}^n, \ \textbf{I} \in \mathbb{G}^s, \ \Pi_{\textsf{\tiny NIZK}} \}

Implementation Challenges

Implemented MProve+ and MProve in Rust over \(\texttt{ed25519, ristretto}\)

Small subgroup attack possible in \(\texttt{ed25519}\)

Implementation Challenges

Implemented MProve+ and MProve in Rust over \(\texttt{ed25519, ristretto}\)

Small subgroup attack possible in \(\texttt{ed25519}\). For a prime \(q\)

Ristretto constructs a prime order group from an Edwards curve

MProve+ over \(\texttt{ristretto}\) allows generalisation for other Edwards curves

|\mathbb{G}_{\textsf{ed}}| = 8q, \ |\mathbb{G}_{\textsf{ris}}| = q

We show conversion of Ristretto points to Edwards 

Wrote an Elligator support over \(\texttt{ed25519}\) to generate random curve points

Running Times for \(\mathbb{G}_{\textsf{ris}}\)

n \ \longrightarrow
s \ \longrightarrow
\text{Running time in mins} \longrightarrow

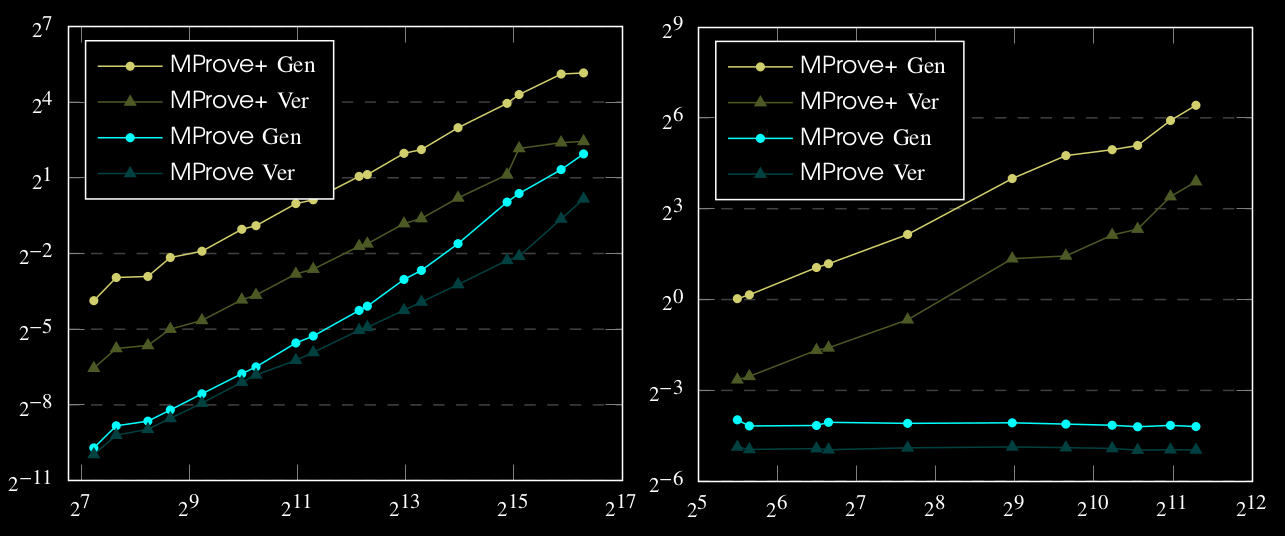
Note: All plots are in log-log scale.

s=100
n=5000
n \approx 2000

Thank

Happy to answer any questions!

you!

Made with Slides.com