A Proof of Reserves Protocol with Short Proofs and a Method to Estimate Amount Upper Bounds for MimbleWimble

Suyash Bagad

Roll Number: 15D070007

Department of Electrical Engineering, IIT Bombay

Dual Degree (B.Tech + M.Tech) Project

Prof. Saravanan Vijayakumaran

Guide

June 24, 2020

Proof of Reserves

Short Proofs

Amount Upper Bounds

MimbleWimble

Outline

Novel proof of reserves protocol with short sizes for MimbleWimble

RevelioBP vs Revelio!

Confidentiality of Amounts in Grin

Presented at Crypto Valley Conference on Blockchain Technology, 2020

Focus on performance trade-offs and implementation

Work accepted at IEEE Security & Privacy on Blockchain, 2020

Graph-based analysis of the Grin Blockchain

Part I

Novel Proof of Reserves Protocol with Short sizes for MimbleWimble

Revelio

\mathcal{C}_{\text{own}}

C = g^{k} \cdot h^{a}

C \in \mathcal{C}_{\text{own}} \implies k \text{ is known}

Each output in MimbleWimble is a Pedersen Commitment

Pedersen Commitments are homomorphic, perfectly hiding and computationally binding

For an amount $a \in \{0,1,\dots,2^{64}-1\}$ and blinding factor $k \in \mathbb{Z}_q$

where $g,h \in \mathbb{G}$ such that DL relation between them is unknown

Revelio

\mathcal{C}_{\text{anon}}

For each $C_i \in \mathcal{C}_{\text{anon}},$ publish the tags $(I_1, \dots, I_n) \in \mathbb{G}^n$ where $ n = |\mathcal{C}_{\text{anon}}|$

Publish $C_{\text{assets}} = \prod_{i \in [n]} I_i,$ and NIZK proofs $\sigma_i \in \mathbb{Z}_q^5 \ \forall i \in [n]$

PoK\big\{\underbrace{(\alpha,\beta,\gamma)}_{\text{secret}} \ | \ \underbrace{(C_i = g^{\alpha} \cdot h^{\beta} \ \wedge \ I_i = g_t^{\alpha} \cdot h^{\beta}) \vee (I_i = g_t^{\gamma}) }_{\text{statement}} \big\}

where $y_i = \mathcal{H}(k_{\text{exch}}, C_i) \in \Z_q$

I_i = \begin{cases} \ g_1^{k_i} \cdot h^{a_i} & \text{if } C_i \in \mathcal{C}_{\text{own}},\\ \ g_1^{y_i} & \text{if } C_i \notin \mathcal{C}_{\text{own}}, \end{cases}

$\implies y_i \longleftrightarrow C_{i} $.

Drawbacks of Revelio

Proof size linear in anonymity set size

(n+1) \text{ in } \mathbb{G}, \ 5n \text{ in } \mathbb{Z}_q

Can we shrink proofs sizes to $\mathcal{O}( \text{log}_2(n))$?

Can we link the blockchain state to the proof of reserves?

Privacy of outputs depends on the anonymity set $n$

RevelioBP!

(

)

\textbf{e}_1 =

(

)

\textbf{e}_2 =

(

)

\textbf{e}_3 =

(

)

\textbf{e}_4 =

(

)

\textbf{e}_5 =

k_1

k_2

k_3

k_4

k_5

(

)

\textbf{k} =

PoK\left\{ \ (\textbf{k} \in \mathbb{Z}_q^s, \ \textbf{E} \in \mathbb{Z}_2^{s \times n}) \ | \ \textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j} \ \wedge \ \ I_j = g_t^{k_j}h^{a_j} \ \forall j \in [s] \ \right\}

Publish tag vector $(I_1, I_2, \dots, I_s),$ $C_{\text{assets}} = \prod_{i \in [n]} I_i$ and NIZK $\Pi_{\text{RevBP}}$

More on RevelioBP

To build $\Pi_{\text{RevBP}},$ we combine the constraints using a scalar $u \leftarrow \mathbb{Z}_q$

\prod_{j \in [s]} \left(g^{-k_j} \cdot g_t^{k_j} \cdot \textbf{C}^{\textbf{e}_{i_j}} \cdot I_j^{-1}\right)^{u^{j-1}} = 1,

\implies g^{- \langle \textbf{u}^s, \textbf{k} \rangle} \cdot g_t^{\langle \textbf{u}^s, \textbf{k} \rangle} \cdot \textbf{C}^{ \textbf{u}^s \textbf{E}} \cdot \textbf{I}^{- \textbf{u}^s} = 1,

We then use Inner Product Argument of the form

PoK \left\{ (\textbf{a}, \textbf{b}) \in \mathbb{Z}_q^N \ | \ P = u^{c}\textbf{g}^{\textbf{a}} \textbf{h}^{\textbf{b}} \wedge c = \langle \textbf{a}, \textbf{b} \rangle \ \right\}

s + 2 \text{log}_2(sn+n+s+3) \text{ in } \mathbb{G}, \ 5 \text{ in } \mathbb{Z}_q

RevelioBP proof size	Revelio proof size

(n+1) \text{ in } \mathbb{G}, \ 5n \text{ in } \mathbb{Z}_q

Performance

We implemented RevelioBP in Rust over $ \mathbb{G} = \texttt{secp256k1}$ elliptic curve

n \ \longrightarrow

s \ \longrightarrow

s=20

n=1000

\text{Proof size in KB} \longrightarrow

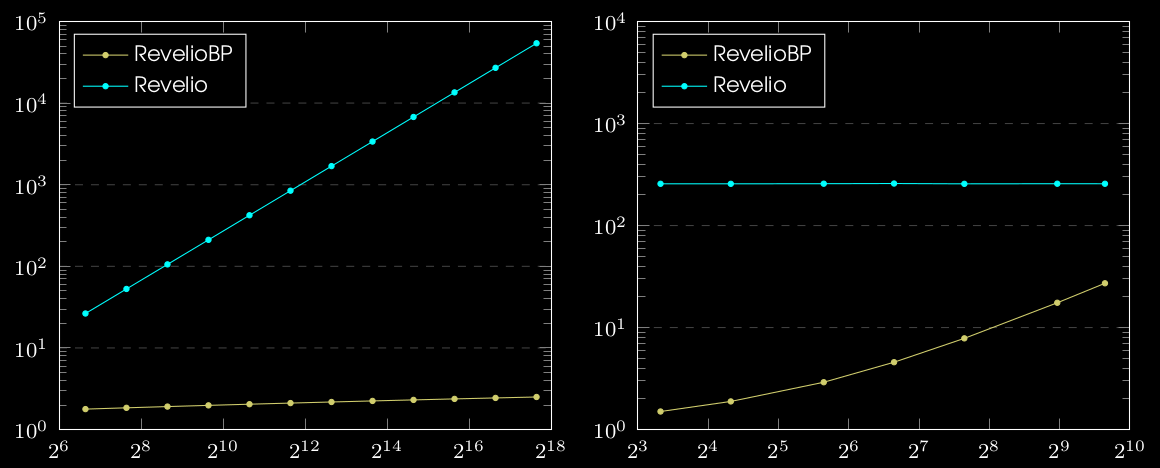
Note: All plots are in log-log scale.

RevelioBP proofs are ~10X shorter that that of Revelio

Performance

RevelioBP proof generation is ~2X slower that of Revelio

n \ \longrightarrow

s \ \longrightarrow

s=20

n=1000

\text{Running time in mins} \longrightarrow

Note: All plots are in log-log scale.

RevelioBP ver. is ~3X faster than its gen. due to multi-exponentiation

Performance Trade-offs

	RevelioBP	Revelio
Proof size
Scalability
Blockchain state
Output privacy
Inflation resistance
Own set size
Running times
Parallelizable

\mathcal{O}(n)

\mathcal{O}(s+\text{log}_2(sn))

\mathcal{O}(sn)

\mathcal{O}(n)

For UTXO set size $n=1.6\times 10^5$ and $s=10^2$

5\text{KB}

32\text{MB}

(164,68)\\[-3pt] \text{min}

(34,34)\\[-3pt] \text{min}

Part II

On the Confidentiality of Amounts in Grin

Estimating Upper Bound on Amounts in Grin

Given an output $P \in \mathbb{G}$ it is infeasible to find the amount it commits to!

Can the transaction rules reveal anything about amounts in Grin?

P = g^k \cdot h^a \in \mathbb{G}

A Grin Block

Block height

Inputs	Outputs

I_1,

O_1, O_2, O_3

Reg. Transaction #2

Inputs	Outputs

I_3, I_4, I_5

O_4

Reg. Transaction #1

Inputs	Outputs
-

O_{\text{cb}}

Coinbase Transaction

I_2

Dandelion

Block height

Inputs	Outputs

I_1

I_2

I_3

I_4

I_5

O_{\text{cb}}

O_1

O_2

O_3

O_4

Cut-through

Block height

Inputs	Outputs

I_1

I_2

I_3

I_4

O_{\text{cb}}

O_1

O_2

O_4

I_5 = O_3!

Block added to Blockchain!

Main Idea

Block height

Inputs	Outputs

I_1^{h_3}

h_3

I_2^{h_3}

O_{\text{cb}}^{h_3}

O_1^{h_3}

O_2^{h_3}

O_3^{h_3}

Fees

f_{h_3}

Block height

Inputs	Outputs

I_1^{h_2}

h_2

O_{\text{cb}}^{h_2}

O_1^{h_2}

O_2^{h_2}

Fees

f_{h_2}

Block height

Inputs	Outputs

I_1^{h_1}

h_1

O_{\text{cb}}^{h_1}

O_1^{h_1}

Fees

f_{h_1}

I_2^{h_1}

\mathcal{A}(I_{1}^{h_2}) = \mathcal{A}(O_{cb}^{h_1}) = r+f_{h_1} \ \implies \ \mathcal{A}(O_{1}^{h_2}) + \mathcal{A}(O_{2}^{h_2}) = r+f_{h_1} - f_{h_2}

\therefore \quad \mathcal{A}(O_{j}^{h_2}) \le r+f_{h_1}-f_{h_2} \quad \forall j=1,2

\therefore \quad \mathcal{A}(I_{1}^{h_3}) + \mathcal{A}(I_{2}^{h_3}) \le 2r + f_{h_1}

\mathcal{A}(I_{1}^{h_3}) = \mathcal{A}(O_{\text{cb}}^{h_2}) = r+f_{h_2}, \quad \mathcal{A}(I_{2}^{h_3}) = \mathcal{A}(O_{2}^{h_2}) \le (r+f_{h_1}-f_{h_2})

\therefore \quad \mathcal{A}(O_{1}^{h_3}) + \mathcal{A}(O_{2}^{h_3}) + \mathcal{A}(O_{3}^{h_3}) \le 2r + f_{h_1} - f_{h_3}

\therefore \quad \mathcal{A}(O_{j}^{h_3}) \le 2r + f_{h_1} - f_{h_3} \quad \forall j=1,2,3

General strategy: Compute number of donor coinbase outputs!

\therefore \quad \mathcal{A}(O_{j}^{h_3}) \le (r+f_{h_1}) + (r+f_{h_2}) - (f_{h_2}+f_{h_3}) \quad \forall j=1,2,3

Grin Blockchain as a DiGraph

We define a directed graph $G = (V,E)$ such that

Nodes $V = V_{\text{bl}} \cup V_{\text{cb}}, $ where $ V_{\text{bl}} $ are blocks and $V_{\text{cb}}$ are coinbase outputs

Edges $E = E_1 \cup E_2$ where

$E_1 = (v_1, v_2) \in V_{\text{cb}} \times V_{\text{bl}} $ if coinbase output $v_1$ is spent in block $v_2$

$E_2 = (v_1, v_2) \in V_{\text{bl}}^2 $ if at least one RTO in block $v_1$ is spent in block $v_2$

$h_1$

$h_2$

$h_3$

Flow Upper Bounds

A vertex $c \in V_{\text{cb}}$ in $G$ is called a donor of a block $b \in V_{\text{bl}}$ if there is a directed path from $c$ to $b$ in $G$.

$1499$

$16$

$1482$

$1469$

$1458$

$1481$

$1489$

$1495$

$1493$

$18$

$1479$

$38$

$33$

$9$

$5$

$7$

Subgraph for $h=1499$, $G^{(h)} = (V^{(h)}, E^{(h)})$ where $V^{(h)} = V^{(h)}_{\text{bl}} \cup V^{(h)}_{\text{cb}}$

$$ \therefore \ \mathcal{A}(O^{h}) \le 7r + \sum_{b \in V_{\text{cb}}^{(h)}} f_b - \sum_{b \in V_{\text{bl}}^{(h)}} f_b $$

Results

Analysis for RTOs in 612,102 blocks (till March 17th, 2020)

$\text{Flow ratio of RTO (FR)} = \frac{\text{Flow upper bound of RTO}}{\text{Trivial upper bound of RTO}}$

For gauging effectiveness of flow upper bounds, we compute and plot

$\text{Block height}$

$\text{Flow ratio}$

$88\%$ blocks have $FR > 0.9$,

$6.6\%$ blocks with $h>10^5$ have $FR < 0.5$

Results

Unspent RTOs depict the current state of the Blockchain (Fig. 2)

$\text{Block height}$

$\text{Flow ratio}$

Jagged pattern in Flow ratio is observed in Fig. 1, Why?

$983$ URTOs have upper bound less that $1800$

$\text{Flow ratio}$

$ \% \text{ of URTO set}$

$95\%$ of $110,149$ URTOs have $FR > 0.9$

Figure 1

Figure 2

Conclusion

Amounts in very few RTOs found to be in a narrow range

Confidentiality of most URTOs is preserved, however...

Transaction structure could reveal some information about amounts inspite of perfectly hiding commitments

Linkability in inputs and outputs could be leveraged for tighter bounds

Would be interesting to design such analysis for Beam, Monero,...

References I

A. Poelstra, "MimbleWimble" [Online], Available:

link

T. P. Pedersen, "Non-Interactive and Information-Theoretic Secure Verifiable Secret Sharing", in Advances in Cryptology - CRYPTO '91, Springer, 1992, pp. 129-140.

M. Möser, et al. “An Empirical Analysis of Traceability in the Monero Blockchain”. Proceedings on Privacy Enhancing Technologies (2018)

"Linking 96% of Grin transactions" [Online], Available:

link

A. Kumar, C. Fischer, S. Tople and P. Saxena, "A traceability analysis of Monero’s blockchain", European Symposium on Research in Computer Security – ESORICS 2017, pp. 153-173, 2017.

References II

A. Dutta and S. Vijayakumaran, "Revelio: A MimbleWimble Proof of Peserves Protocol", in Crypto Valley Conference on Blockchain Technology (CVCBT), June 2019, pp. 7–11.

R. W. F. Lai, V. Ronge, T. Ruffing, D. Schröder, S. A. K. Thyagarajan, and J. Wang, “Omniring: Scaling private payments without trusted setup,” in Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, November 2019

"RevelioBP simulation code" [Online], Available:

link

B. Bünz, J. Bootle, D. Boneh, A. Poelstra, P. Wuille, and G. Maxwell, "Bul-
letproofs: Short proofs for confidential transactions and more", in IEEE
Symposium on Security and Privacy (SP), May 2018, pp. 315–334.

Thank

Happy to answer any questions!

you!

Appendix I

Read on to dive in deeper!

Pedersen Commitment

A cryptographic tool to hide a secret $a \in \mathbb{F}_q, $ computed as

P = \texttt{com}(a,r) = g^{r} \cdot h^{a}

where $r \in \mathbb{F}_q, g,h \in \mathbb{G}$ and DL relation between them is unknown

Homomorphic

- Given $ P_1 = \texttt{com}(a_1, r_1), \ P_2 = \texttt{com}(a_2, r_2) $

P_1 \cdot P_2 = \texttt{com}(a_1 + a_2, r_1+r_2)

Perfectly Hiding

- Given $ P = \texttt{com}(a,r) \in \mathbb{G} $, it is infeasible to find $a$ or $r$

Computationally Binding

- Given $ P = \texttt{com}(a,r) \in \mathbb{G} $, it is infeasible for a

computationally bounded adversary to find $ (a^{\prime}, r^{\prime})$ s.t. $P = \texttt{com}(a^{\prime}, r^{\prime})$

Zero Knowledge Proofs

Coke from Bottle

Coke from Can

Victor

Peter

$x$

$V$

$P$

Zero Knowledge Proofs

Guess?

Coke from Can

Bottle!

Victor

Peter

\langle P, V \rangle (x) = \begin{cases} 1 & \text{if } V \text{ accepts} \\ 0 & \text{if } V \text{ rejects} \end{cases}

Zero Knowledge Proofs

Try again!

Coke from Can

Victor

Peter

Coke from Bottle

Zero Knowledge Proofs

Victor

Peter

Coke from Bottle

Can!

If $P$ actually knows the taste, $ \Pr[ \langle P,V \rangle(x) = 1 ]$ = 1

If $P$'s claim is wrong, $ \Pr[ \langle P,V \rangle(x) = 1 ] = \left(\frac{1}{2}\right)^2 $

$\implies$ Completeness!

$\implies$ Soundness!

Appendix II

Read on to dive in deeper!

More on a Grin Block

Block height
Kernel offset

Inputs	Outputs

I_1

k_{\text{off}} \in \mathbb{F}_q

I_2

I_3

I_4

O_{\text{cb}}

O_1

O_2

O_4

Fees

f_{\text{cb}}, f_1,f_2

Kernel
Excesses

X_{\text{cb}},X_1,X_2

RTO

$$ \sum_{i=1,2,4}O_i+ \left(\sum_{i=1,2} f_i\right) H - \sum_{i=1}^{4}I_i = \sum_{i=1,2}X_i + k_{\text{off}}G$$

A block contains $n$ kernels, $n =$ #Transactions

Each kernel contains fee and a kernel excess

Coinbase fee $f_{\text{cb}} = 0$, mining reward $r = 60$ grin

Each kernel also contains a Schnorr signature proving that $X_i = x_iG$ for some $x_i \in \mathbb{F}_q$

Block validation check:

Related Work

Listening to ~600 peer nodes, transactions could be traced to their origin before they are aggregated

Ivan Bogatty claimed to have traced 96% of all Grin transactions

Image credits: https://github.com/bogatyy/grin-linkability

Related Work

A. Kumar et al. demonstrated 3 attacks on traceability of inputs in Monero transactions, showing that In $87\%$ of cases, the real output being redeemed can be identified!

Idea#1: $65\%$ transactions have 0 mix-ins as of Feb, 2017!

Idea#2: An input being spent in a ring is the one with the highest block height, where it appeared as a TXO.

Image credits: https://eprint.iacr.org/2017/338.pdf

Related Work

M$ \ddot{o} $ser et al. presented traceability analysis of Monero similar and concurrent to that of Kumar et al's work

Proposed a novel Binned Mixin Sampling strategy as a counter-measure

Characterised Monero usage based on user-behaviour

https://arxiv.org/pdf/1704.04299.pdf