HyperPlonk
Part \(1\)
Arithmetic Circuit
- A typical computational problem: find solutions to the equation (i.e. \(\textsf{stmt}\))
\(w_1^2 \cdot w_2 + w_1 + 1 = 22\)
- Witness: \(w \equiv (w_1=3, w_2=2)\), public inputs: \(\ell \equiv (c=1, z=22)\)
- I can convince you that I know a solution \(w\) to \(\{\textsf{stmt}, \ell\}\) without revealing \(w\)
- PLONK: Circuit size: \(n=4\), prover: \(\mathcal{O}(n\cdot\text{log}n)\), proof size and verifier: \(\mathcal{O}(1)\)
Gate Constraints
| Gate | Constraint |
- A gate constraint with inputs \((a, b, c)\) is written as:
- Prove that each gate identity is zero
- Convert vectors \((a, \dots, \textcolor{grey}{\textsf{q}_C})\) to polynomials:
Gate Constraints
Gate Constraints
- Plonk uses univariate polynomials to represent witness and selector vectors
- The arithmetic identity must be 0 over \(H\)
- That is: \(\forall x \in H\) we should have
Gate Constraints

- We know that \(f_{\text{arith}}(X)\) must be \(0\) on \(H\)
- Thus, the set of roots of \(f_{\text{arith}}(X)\) must be \(\supseteq H\)
- Thus, if we compute \(t_{\text{arith}(X)} = \frac{f_{\text{arith}}(X)}{Z_H(X)}\) and send it to verifier, we're done!
Copy Constraints
- Compute permutation values: \(z_1=1\) and for \(i \in \{1, 2, \dots, n-1\}\)
- In terms of polynomials, we need to prove: \(\forall x \in H\)
Drawbacks of Plonk
- Compute quotient polynomial \(t(X)\)
- In summary, we convert identities into univariate polynomial identities.
- Then, we prove that each of the polynomial identities is 0 on a subgroup \(H\).
- Computing \(t(X)\) requires the \(\textcolor{forestgreen}{4n}\)-evaluation form of polynomials.
- Thus, lots of FFTs and iFFTs needed for the \(\textcolor{forestgreen}{4n}\)-evaluation form
- Problem 1: For zkEVM circuits (\(\approx 2^{30}\)), FFTs become the bottleneck as \(\mathcal{O}(4n. \text{log}(4n))\)
- Problem 2: High-degree gates increase the FFT and MSM complexity
Alternative Polynomial Representation
Alternative Polynomial Representation
- Use \(\mu\)-variate polynomials with \(\mu=\text{log}_2n\)
- Boolean hypercube: \(B_\mu = \{0,1\}^\mu\)
- Prove that a multi-variate polynomial is 0 on \(B_\mu\)
- Use sumcheck! But how?
- Convert all of the identities to sumcheck!
Multi-variate Polynomials
- Boolean hypercube: \(B_\mu = \{0,1\}^\mu\), let \(n:=2^\mu\)
- \(\mathcal{F}_\mu^{\le d}:\) Set of multi-variate polynomials \(\mathbb{F}[X_1, X_2, \dots, X_\mu]\) s.t. \(\text{deg}(X_j) \le d \ \ \forall j \in [\mu]\)
- Given \(f(X_1, X_2, X_3)\), we define its MLE \(\hat{f}\in \mathcal{F}_\mu^{\le 1}\) as:
- Merge two \(f,g\in \mathcal{F}_{\mu}\) to get \(h \in \mathcal{F}_{\mu+1}\)
HyperPlonk Buildup
- Gate constraint: \(\forall \vec{x} \in B_\mu\)
- Copy constraint: permutation function \(\sigma: B_{\mu+2} \rightarrow B_{\mu+2}\)
Gate Constraint
- Gate constraint: \(\forall \vec{x} \in B_\mu\)
- Sample a challenge vector \(\vec{r} \leftarrow \mathbb{F}^{\mu+2}\) and compute:
- ZeroCheck: Run a sum-check on \(\hat{f}_{\textsf{gate}}(\vec{X})\) with sum 0.
Copy Constraint
- The permutation check: let \(\sigma: B_\mu \rightarrow B_\mu\) and \(f, g \in \mathcal{F}_{\mu}^{\le d}\) s.t.
- Now we need to show that the sets of tuples are equal:
- ProductCheck: Run a product-check on \(\frac{f'}{g'}(\vec{X})\) with product 1.
- Define permutation selectors as:
- Define \(f'(\vec{x}) := f(\vec{x}) + \textcolor{grey}{\beta}s_{\textsf{id}}(\vec{x}) + \textcolor{grey}{\gamma}\) and \(g'(\vec{x}) := g(\vec{x}) + \textcolor{grey}{\beta}s_{\sigma}(\vec{x}) + \textcolor{grey}{\gamma}\)
- Its enough to show that
HyperPlonk PIOPs
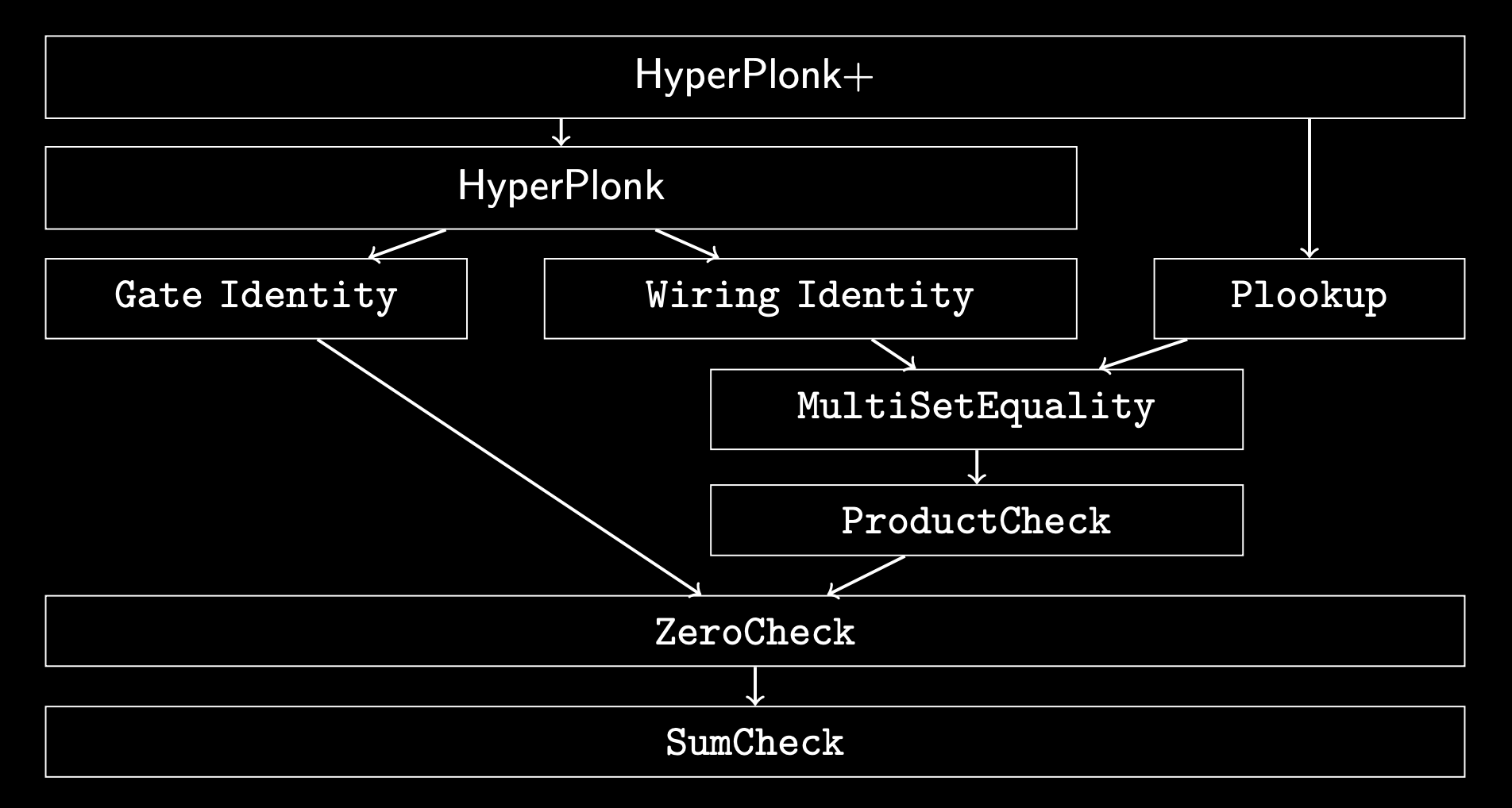
\(\texttt{Gate Constraint}\)
\(\texttt{Copy Constraint}\)



Sumcheck
- Given a polynomial \(g: \mathbb{F}^\mu \rightarrow \mathbb{F}\) and \(X = \{x_i\}_{i \in [\mu]}\) compute the sum
- Intuition: evaluation on a boolean hypercube

\(g(x,y) = \frac{-4x}{(x^2+y^2+1)}\)
- Naively, a verifier would require \(2^\mu\) evaluations of \(g(.)\)
- Sumcheck protocol requires \(\mathcal{O}(\mu + \lambda)\) verifier work
- Here \(\lambda\) is the cost to evaluate \(g(.)\) at some \(r \in \mathbb{F}^{m}\)
- Prover's work is \(\mathcal{O}(2^\mu)\), i.e. linear in no of constraints
Sumcheck
- Honest prover starts by computing \(v = \sum_{X \in \{0,1\}^\mu}g(x_1, x_2, \dots, x_\mu)\)
\(g_1(\textcolor{orange}{X_1}) := \sum_{x_2\dots}g(\textcolor{orange}{X_1},x_2, \dots, x_m)\)
\(g_2(\textcolor{orange}{X_2}) := \sum_{x_3\dots}g(\textcolor{green}{r_1}, \textcolor{orange}{X_2}, x_3, \dots, x_m)\)
\(v \stackrel{?}{=} g_1(0) + g_1(1)\)
\(g_1(\textcolor{green}{r_1}) \stackrel{?}{=} g_2(0) + g_2(1)\)
\(g_3(\textcolor{orange}{X_3}) := \sum_{x_4\dots}g(\textcolor{green}{r_1}, \textcolor{green}{r_2}, \textcolor{orange}{X_3}, x_4, \dots, x_m)\)
\(g_\mu(\textcolor{orange}{X_\mu}) := g(\textcolor{green}{r_1}, \textcolor{green}{r_2}, \dots, \textcolor{green}{r_{\mu-1}}, \textcolor{orange}{X_\mu})\)
\(g_2(\textcolor{green}{r_2}) \stackrel{?}{=} g_3(0) + g_3(1)\)
\(g_{\mu-1}(\textcolor{green}{r_{\mu-1}}) \stackrel{?}{=} g_\mu(0) + g_\mu(1)\)
\(g_{\mu}(\textcolor{green}{r_{\mu}}) \stackrel{?}{=} g(\textcolor{green}{r_1}, \textcolor{green}{r_2}, \dots, \textcolor{green}{r_\mu})\)
Prover \(\mathcal{P}\)
Verifier \(\mathcal{V}\)
\(g_1\)
\(r_1\)
\(g_2\)
\(g_3\)
\(g_\mu\)
\(r_{\mu-1}\)
\(r_2\)
\(\vdots\)
\(\vdots\)
\(\vdots\)
Sumcheck Costs

-
Prover costs:
- In round \(i\in[\mu]\), evaluate \(g_i(\vec{x})\):
- \(g_i(\textcolor{orange}{X}) := \sum_{\vec{x}\in B_{\mu-i}}g(\textcolor{green}{r_1, \dots, r_{i-1}}, \textcolor{orange}{X}, \vec{x})\)
- \(\text{deg}_X(g_i) := \text{deg}_{x_i}(g)\)
- No of evaluations: \(|B_{\mu-i}| = 2^{\mu-i}\)
- Total evaluations: \(\sum_{i}\text{deg}_{x_i}(g) \cdot 2^{\mu-i}\)
- Thus, total evaluations \(O(2^\mu)\) if degree of each variable is \(O(1)\)
-
Verifier costs:
- In round \(i\), evaluate \(g_i(0), g_i(1), g_{i-1}(r_{i-1}) \implies O(\mu)\)
- Cost of evaluating \(g(\vec{x})\) on \(\vec{x} = (r_1, \dots, r_\mu)\)
-
Proof size:
- \(\sum_{i} (\text{deg}_{x_i}(g) + 1) \equiv O(\mu)\) if degree of each variable is \(O(1)\)
Non-Interactive Sumcheck
- Proof size: \(\#\mathbb{G} = 2\mu+2\) and \(\# \mathbb{F} = 3\mu\)
-
Prover computation with KZG:
- \(2\mu+2\) MSMs of size \((d+1),\)
- Evaluations: \(d\times 2^{\mu}\)
- Verifier: 1 MSM of \(O(\mu)\) and 1 pairing
-
Prover computation with Shplonk:
- \(\mu+2\) MSMs of size \((d+1),\)
- Evaluations: \(d\times 2^{\mu}\)
Non-Interactive Sumcheck 🚀
- Proof size: \(\mathbb{G} \rightarrow 2\mu+1, \mathbb{F} \rightarrow 2\mu\)
- Prover computation improvement: \(\mu+2\) MSMs of size \(d\)
- The verifier can compute the other two evaluations using \(\textcolor{lightgreen}{g_i(0), g'(r_i)}\)
- This would require prover to open \(g'_i(X)\) only at \(r_i\):