Price Modelling of Stablecoins
Recall - GBM & More
- Stock prices in traditional finance are modeled using GBM
\begin{aligned}
\frac{\Delta S_t}{S_t} = \mu \Delta t + \sigma \sqrt{\Delta t} \varepsilon
\end{aligned}
\begin{aligned}
\text{log}\left(\frac{ S_t}{S_0}\right) \sim \mathcal{N}\left(\left(\mu - \frac{\sigma^2}{2}\right)t , \sigma \sqrt{t}\right)
\end{aligned}
\implies
- When \(p > 0.5\), the expected growth rate of the price of the asset is
\begin{aligned}
G_{\text{HODL}} = \mu - \frac{\sigma^2}{2}
\end{aligned}
- Here the term \(-\frac{\sigma^2}{2}\) is known as the volatility drag.
- In the same case of \(p > 0.5\), if we have \(\frac{2\sqrt{\mu}}{\sqrt{3}} < \sigma < 2\sqrt{\mu},\) we have
\begin{aligned}
G_{\text{LP}} = \frac{1}{2}\left(\mu - \frac{\sigma^2}{4}\right) > G_{\text{HODL}}
\end{aligned}
Volatility
Random process
Markov process
Drift
Basis Cash
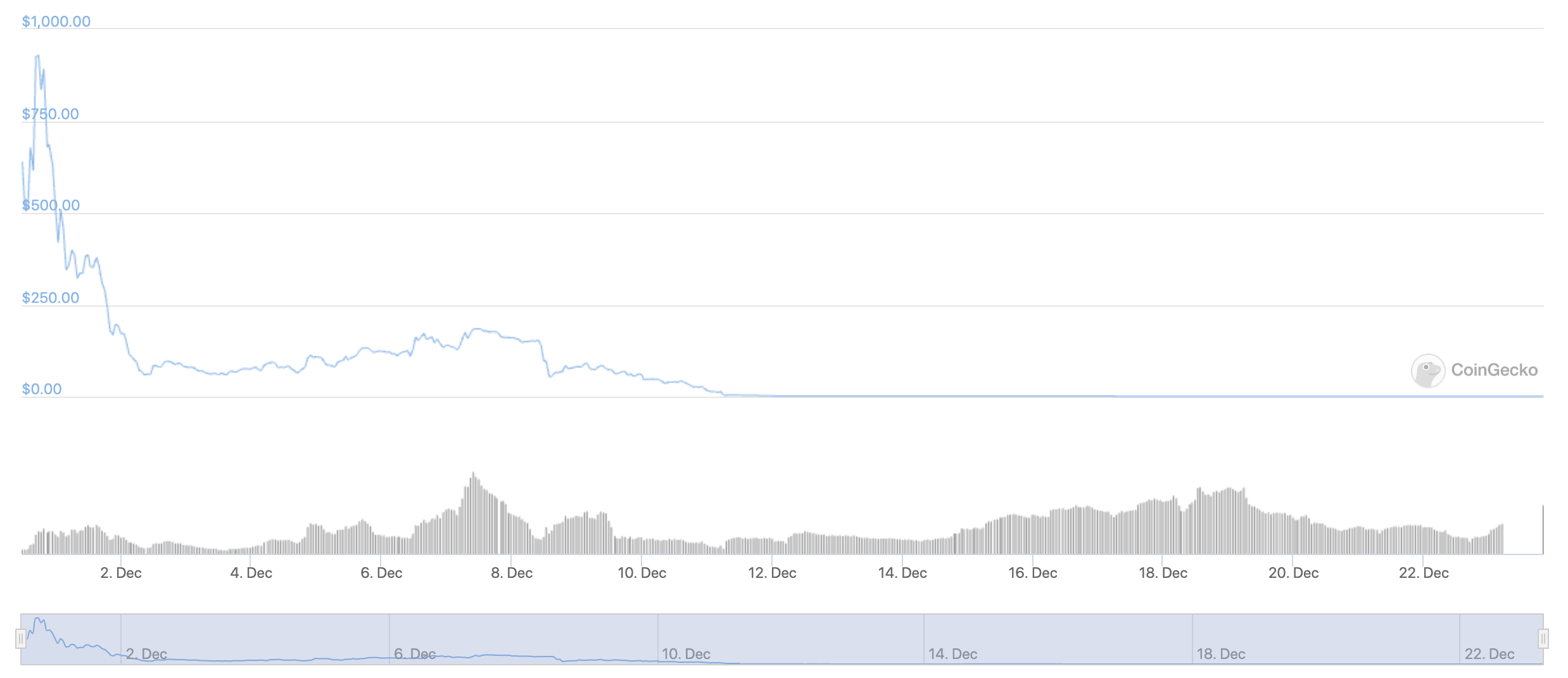
Price Profile (BAC/USD)
Stability starts
Basis Cash
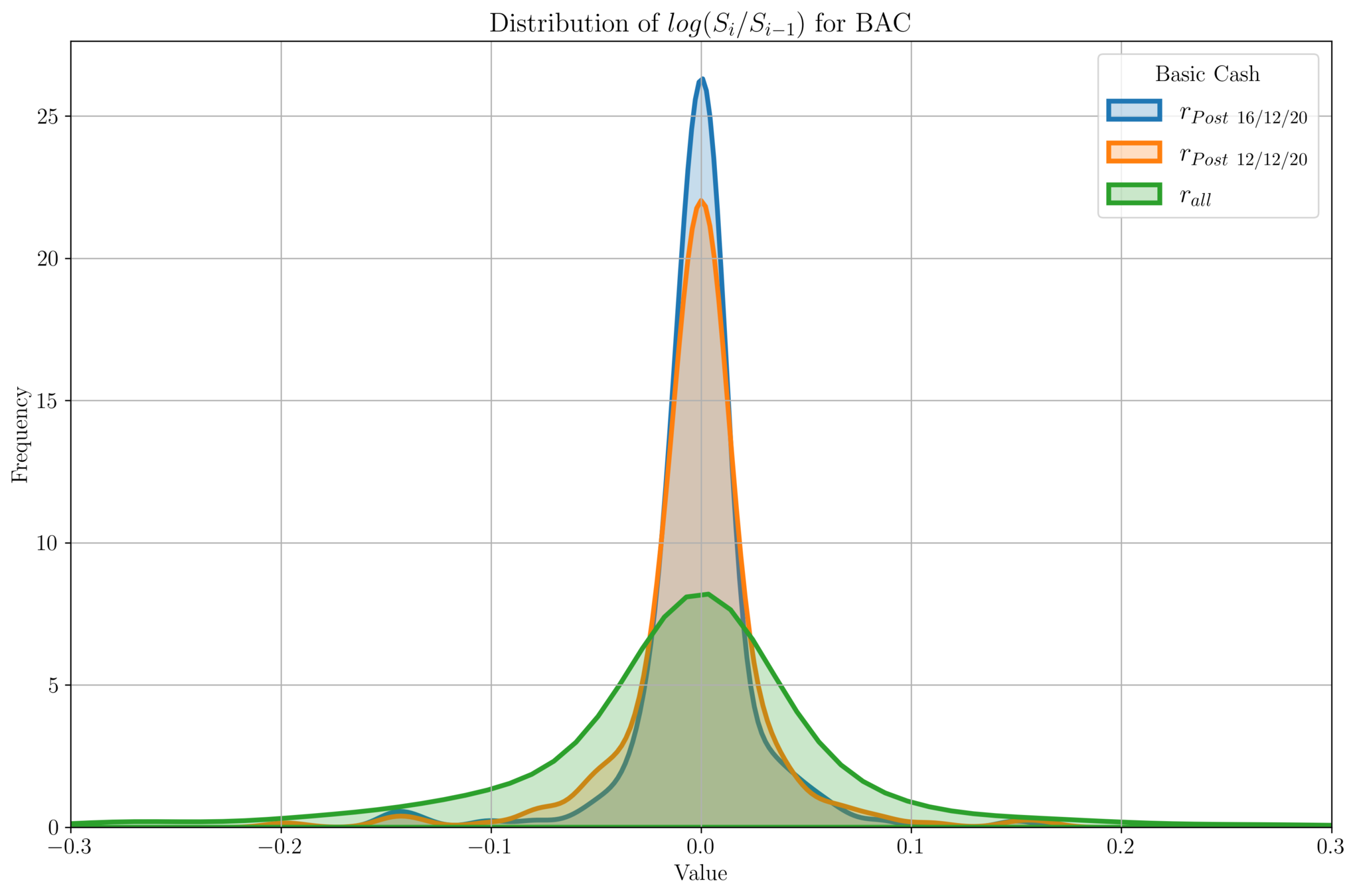
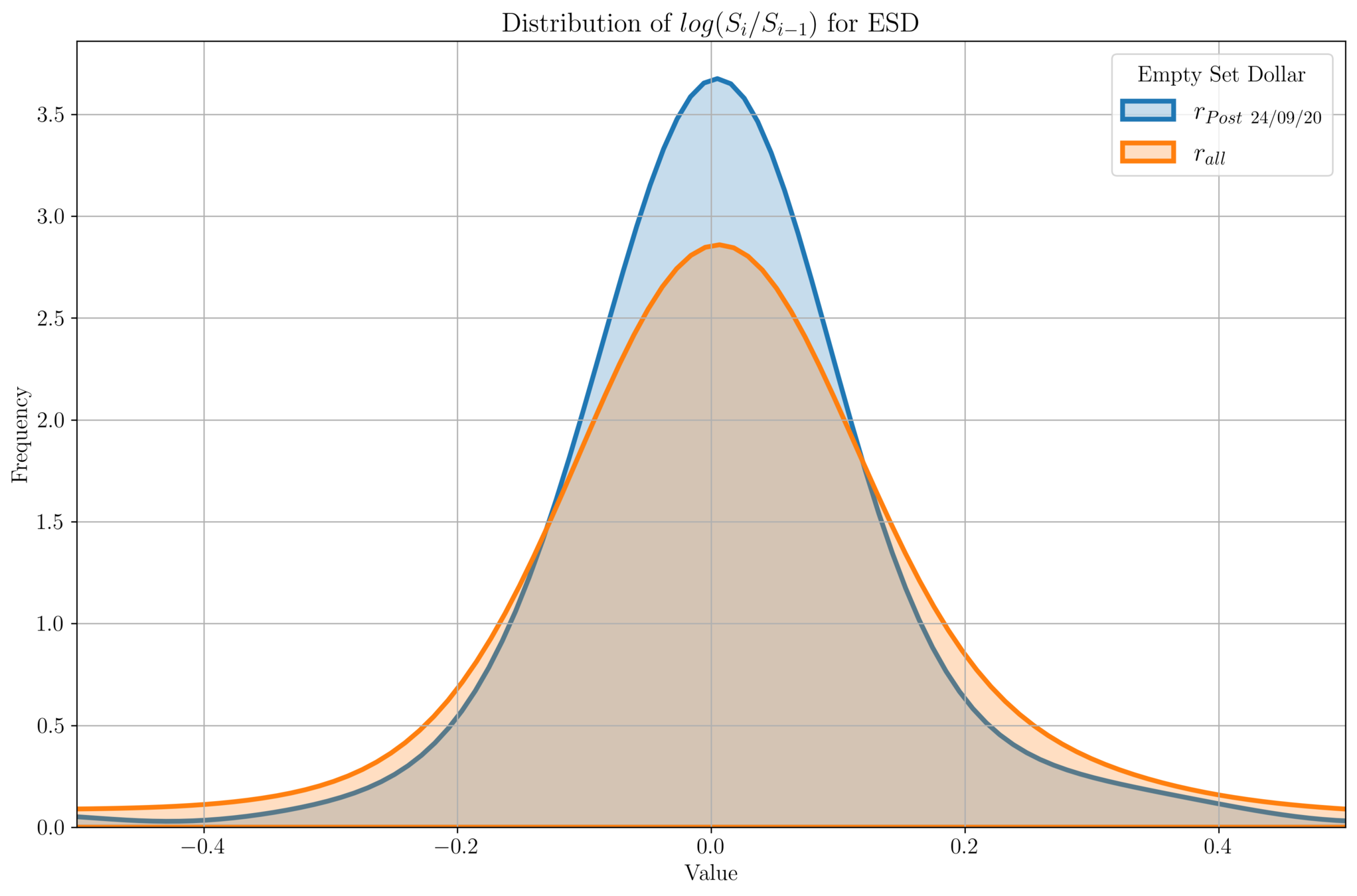
- We plot the distribution of \(\text{log}\left(\frac{S_i}{S_{i-1}}\right)\) for price data \(\{S_i\}\).
- Ideally for stablecoins, we should have a delta function at \(X = 0\).
- For all the price data, we see a Gaussian distribution centered at 0.
- For all-time price data, we see a spread around \([-0.2, 0.2]\).
- For more recent price data (which is stabilized around \(\$1\), we see the variance gets smaller.
Ampleforth
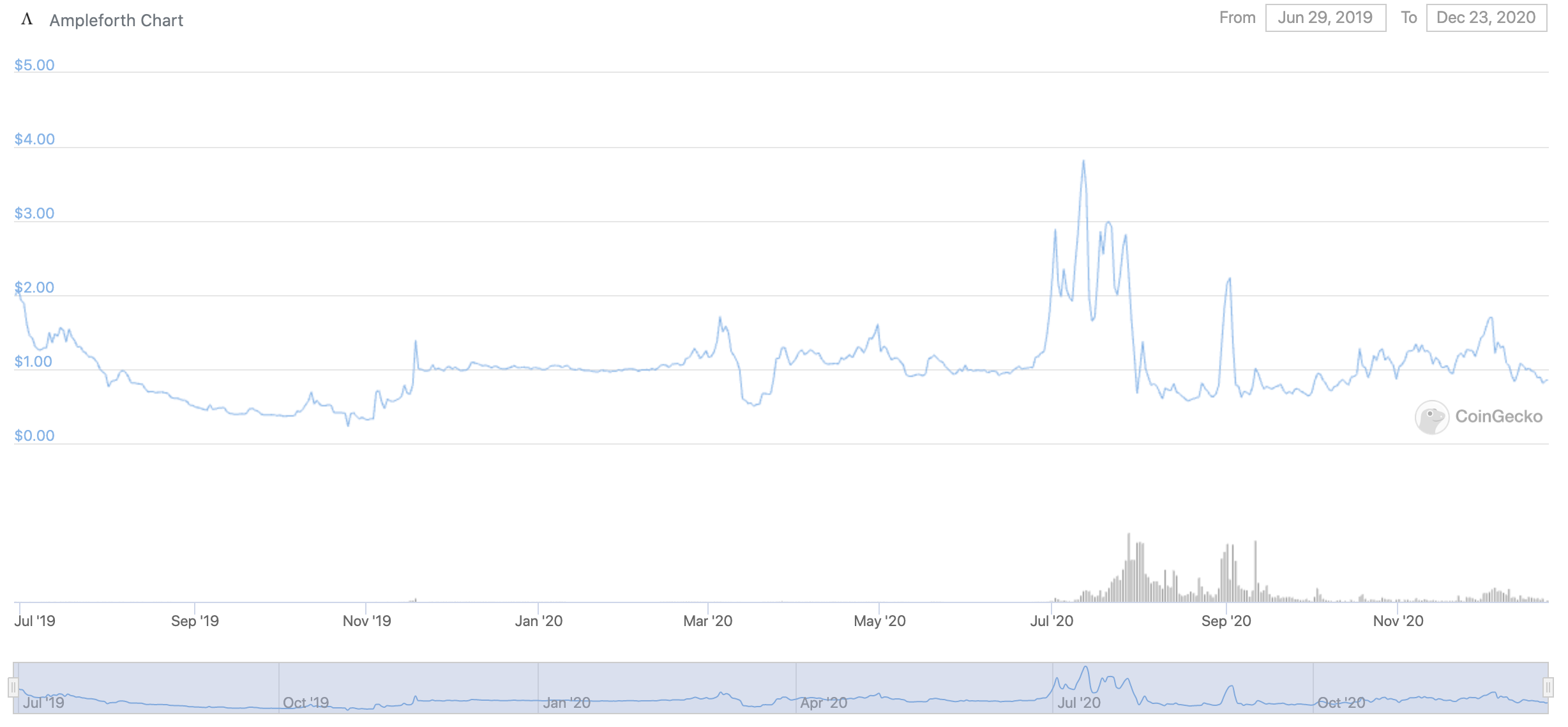

- Prices before June 26th are more stable (\(\sim \$1\)).
- Volume trade increase led to price fluctuations.
- Here too, we expect the distribution of prices to be Gaussian.
Ampleforth
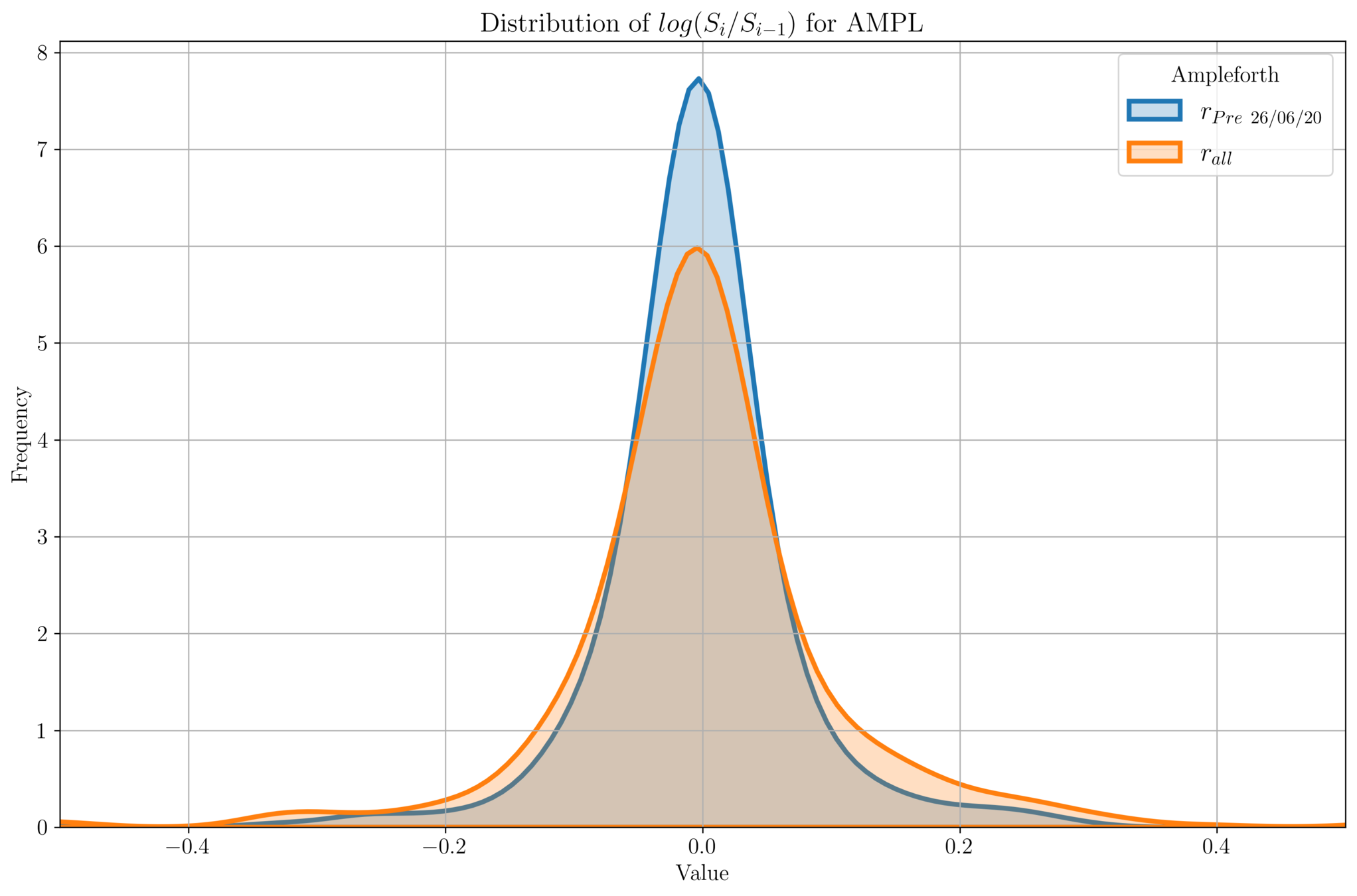
Empty Set D\(\phi\)llar
Empty Set D\(\phi\)llar
Drift & Volatility Analysis
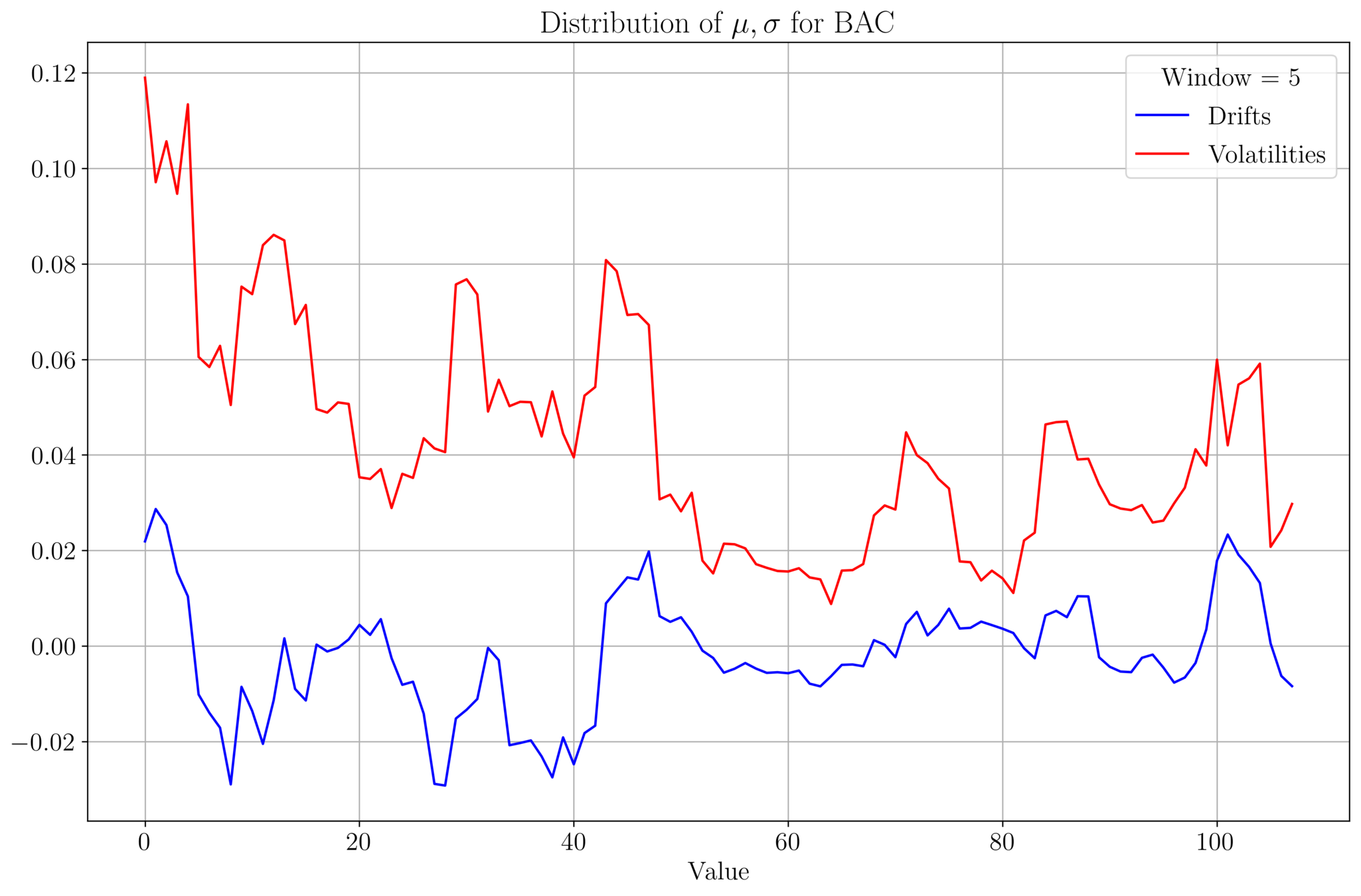
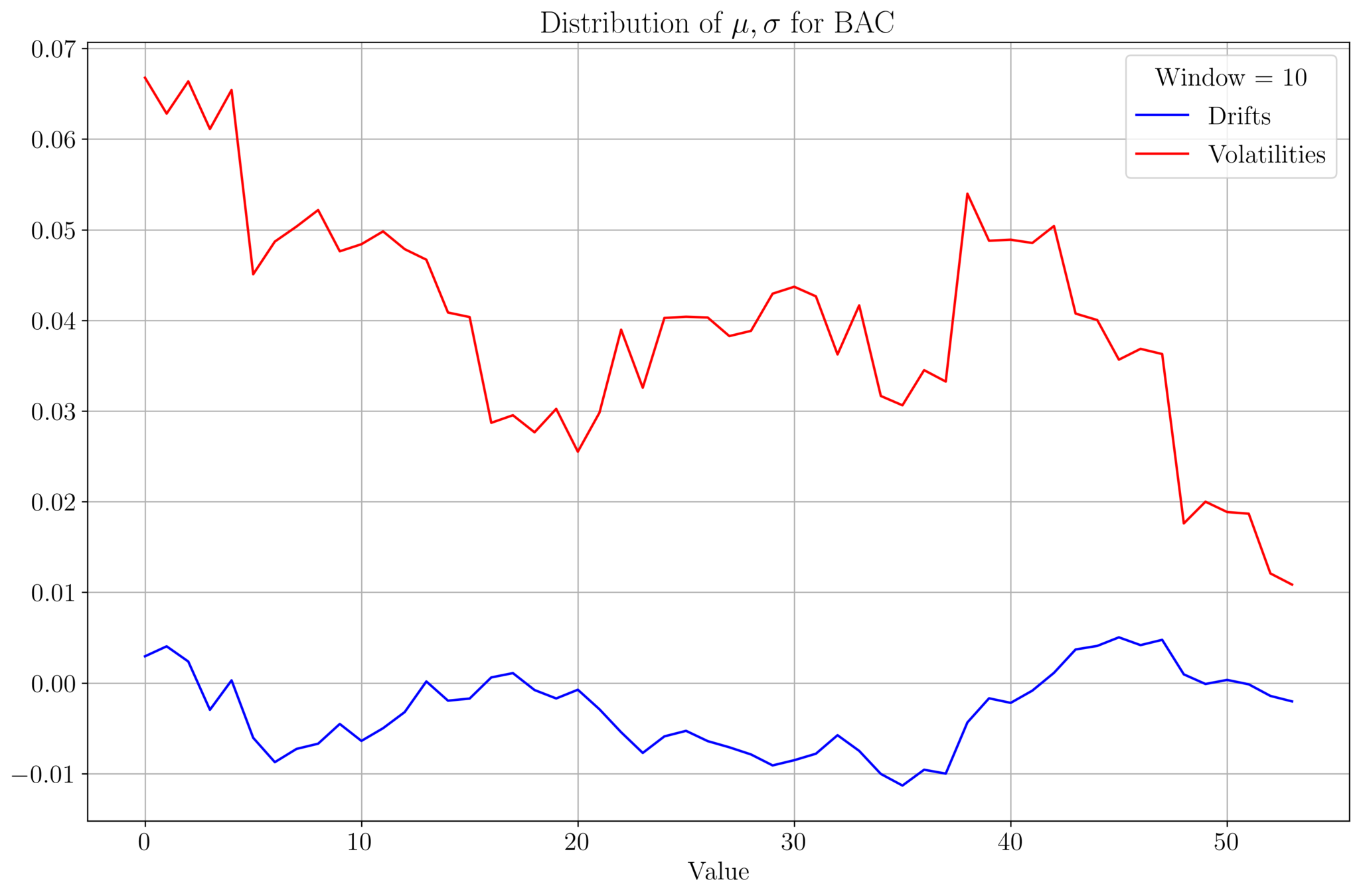
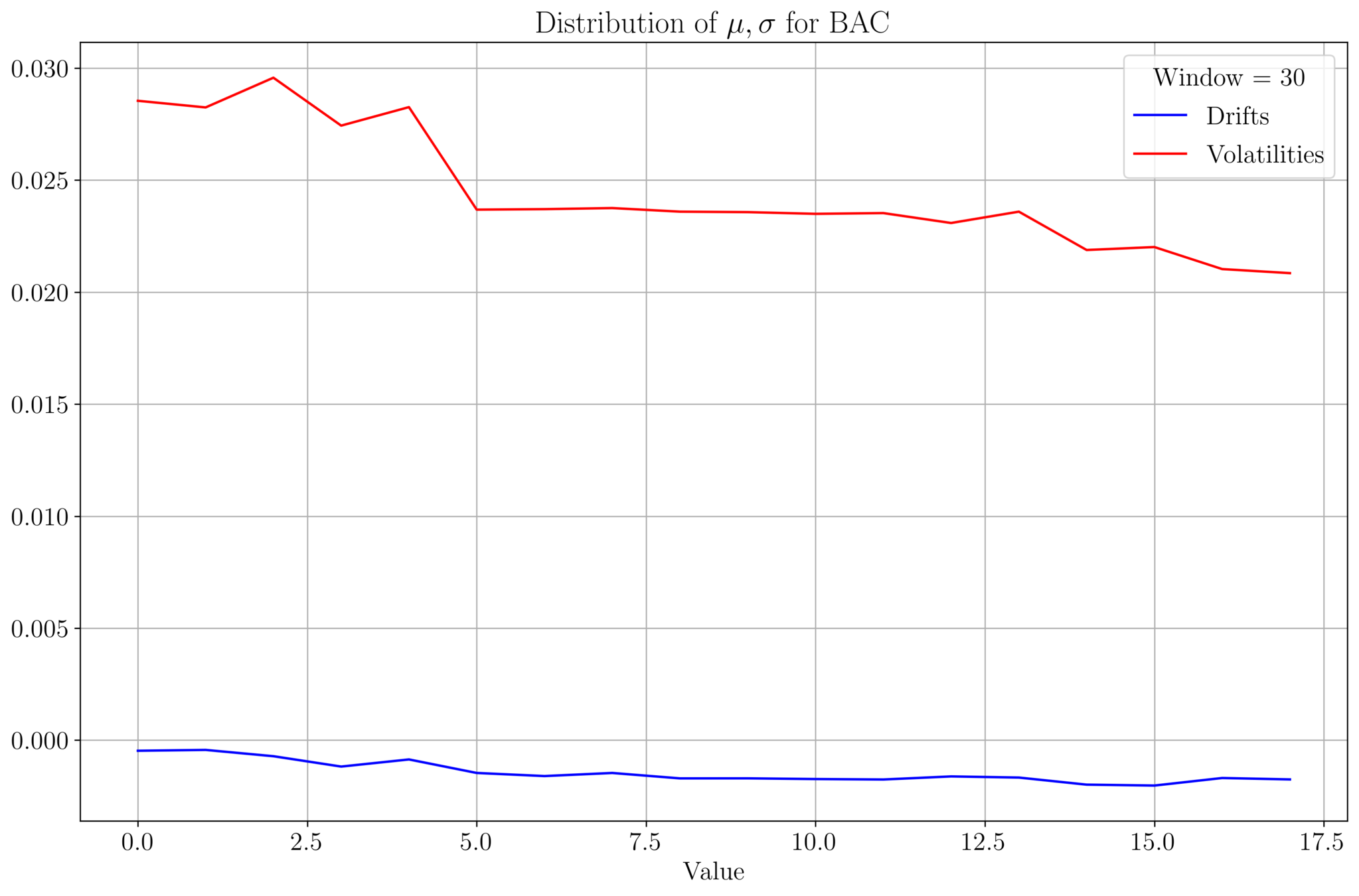
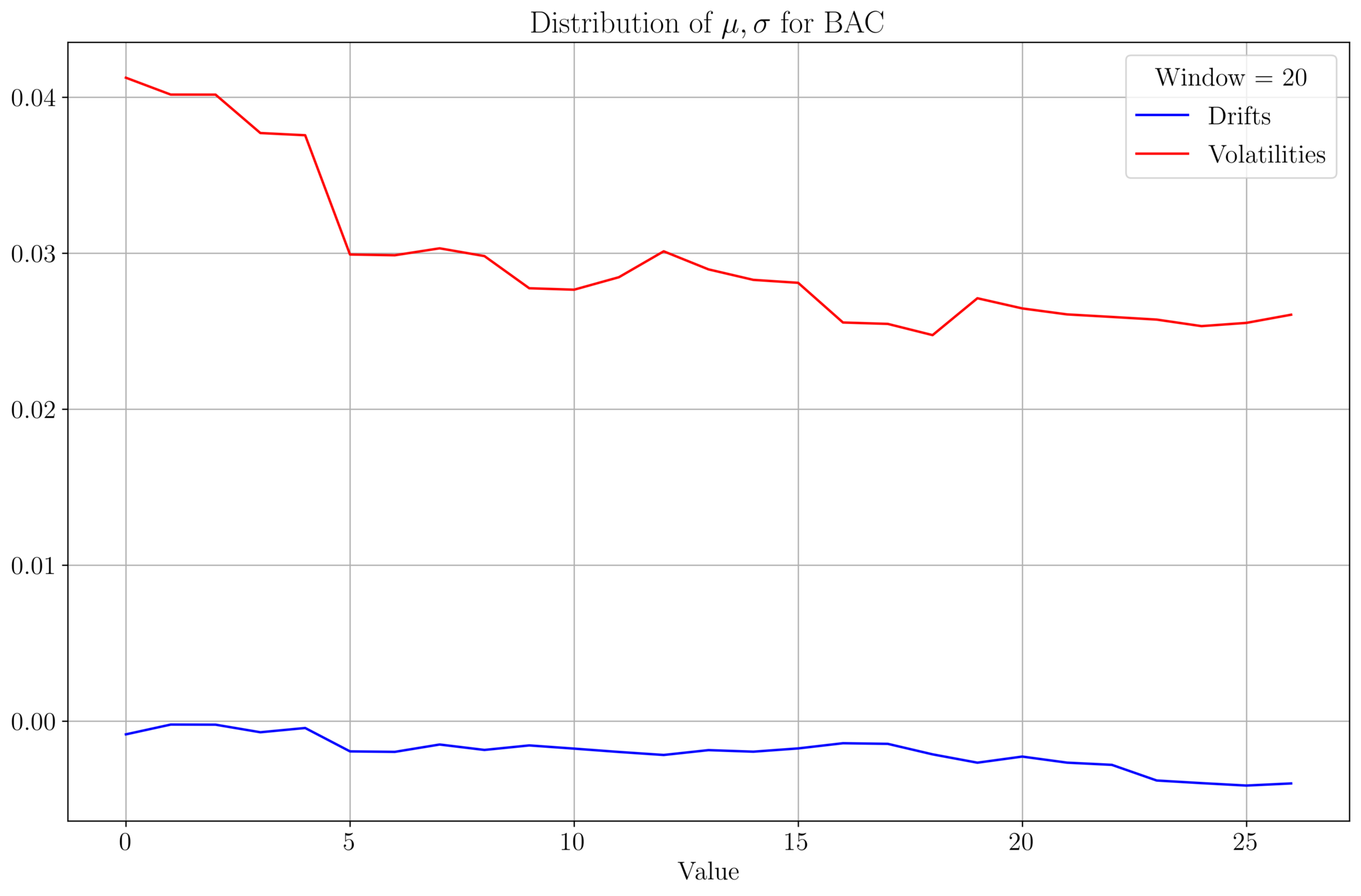
- We analyse \(\mu, \sigma\) of BAC prices for a data set of size 542.
- Plot of \((\mu, \sigma)\) values for a given window size:
Drift & Volatility Analysis




- As the window size increases, \(\mu, \sigma\) tends to stabilize
- \(\mu\) and \(\sigma\) roughly follow a similar profile
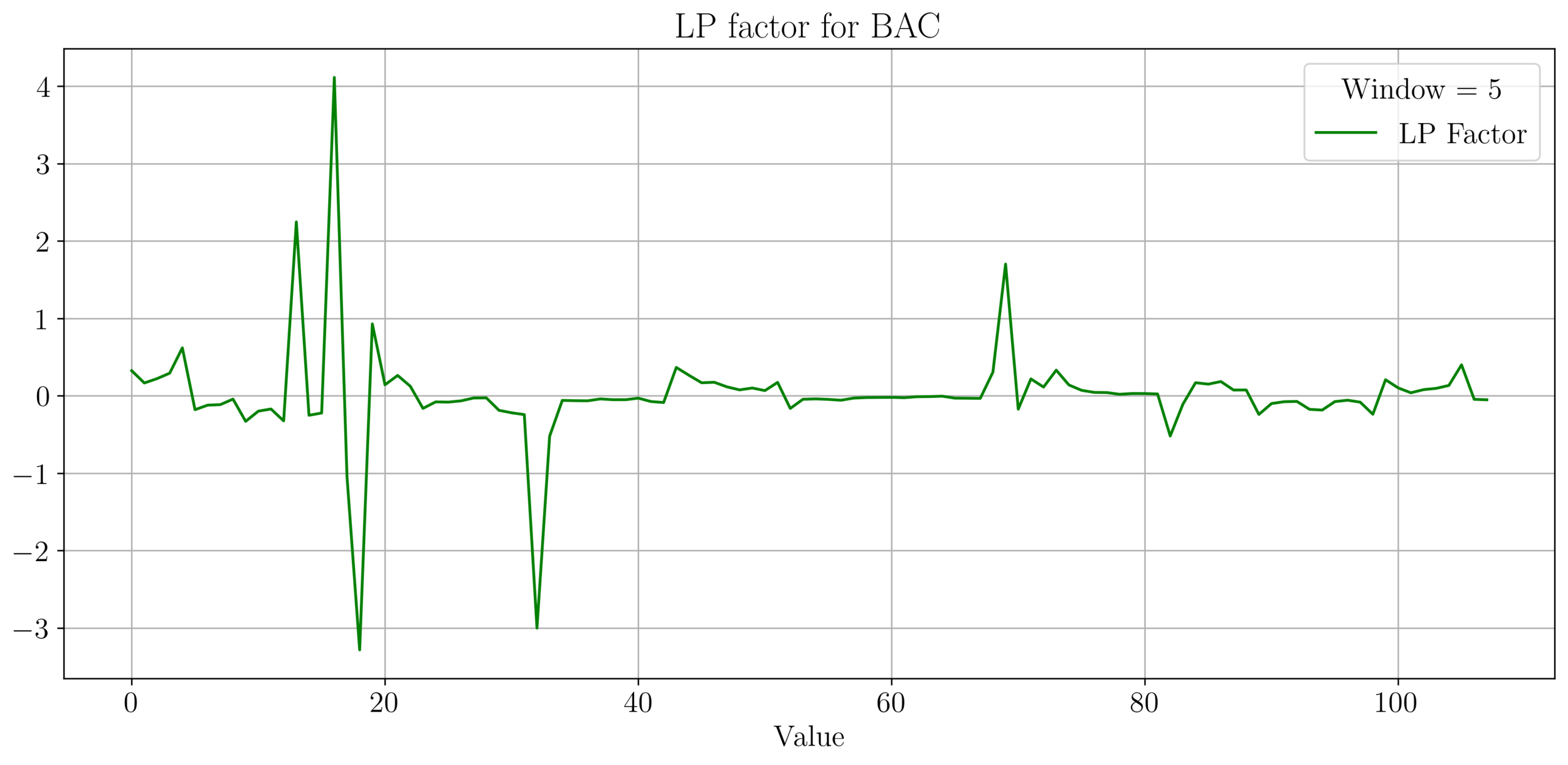
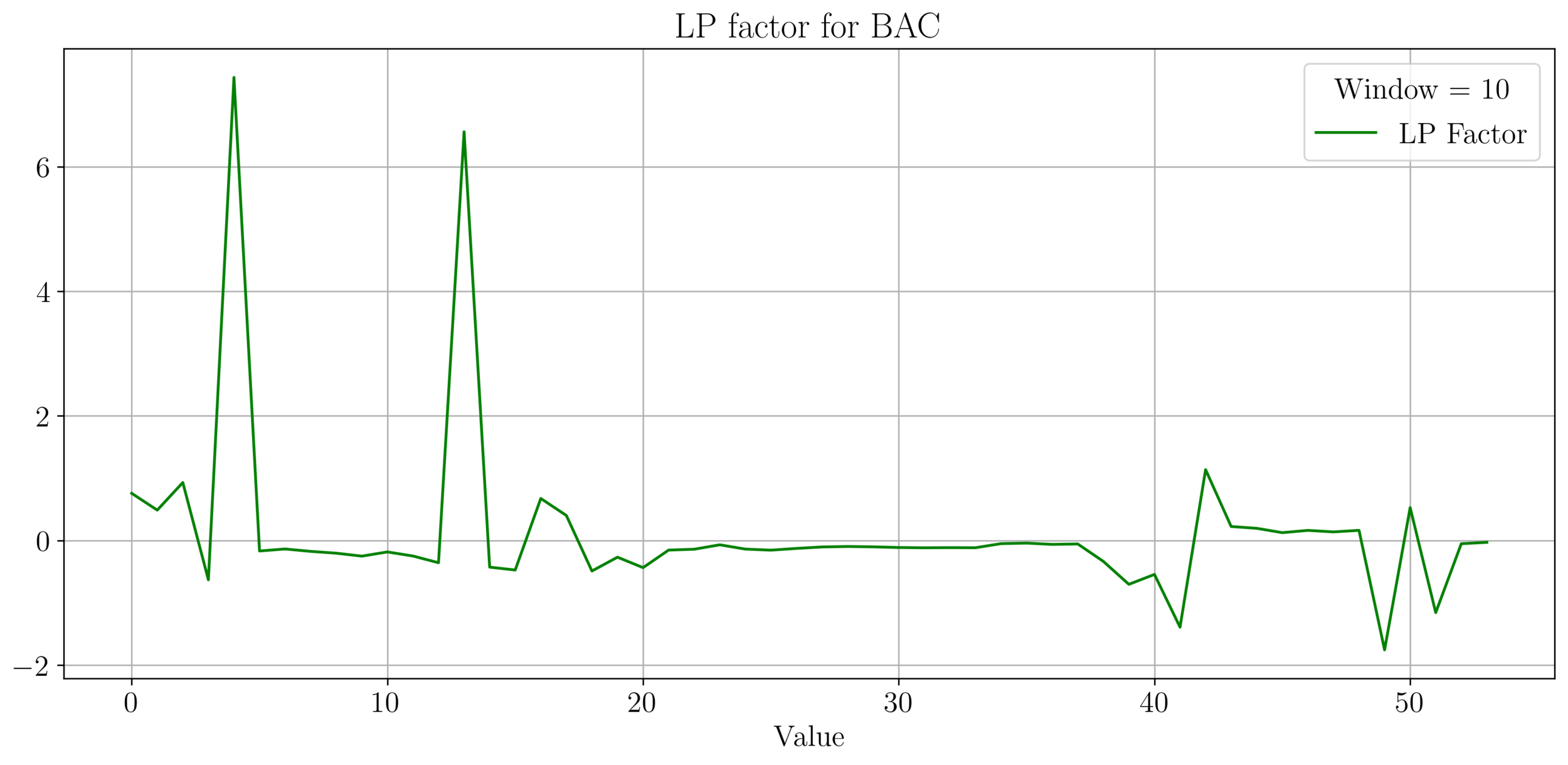
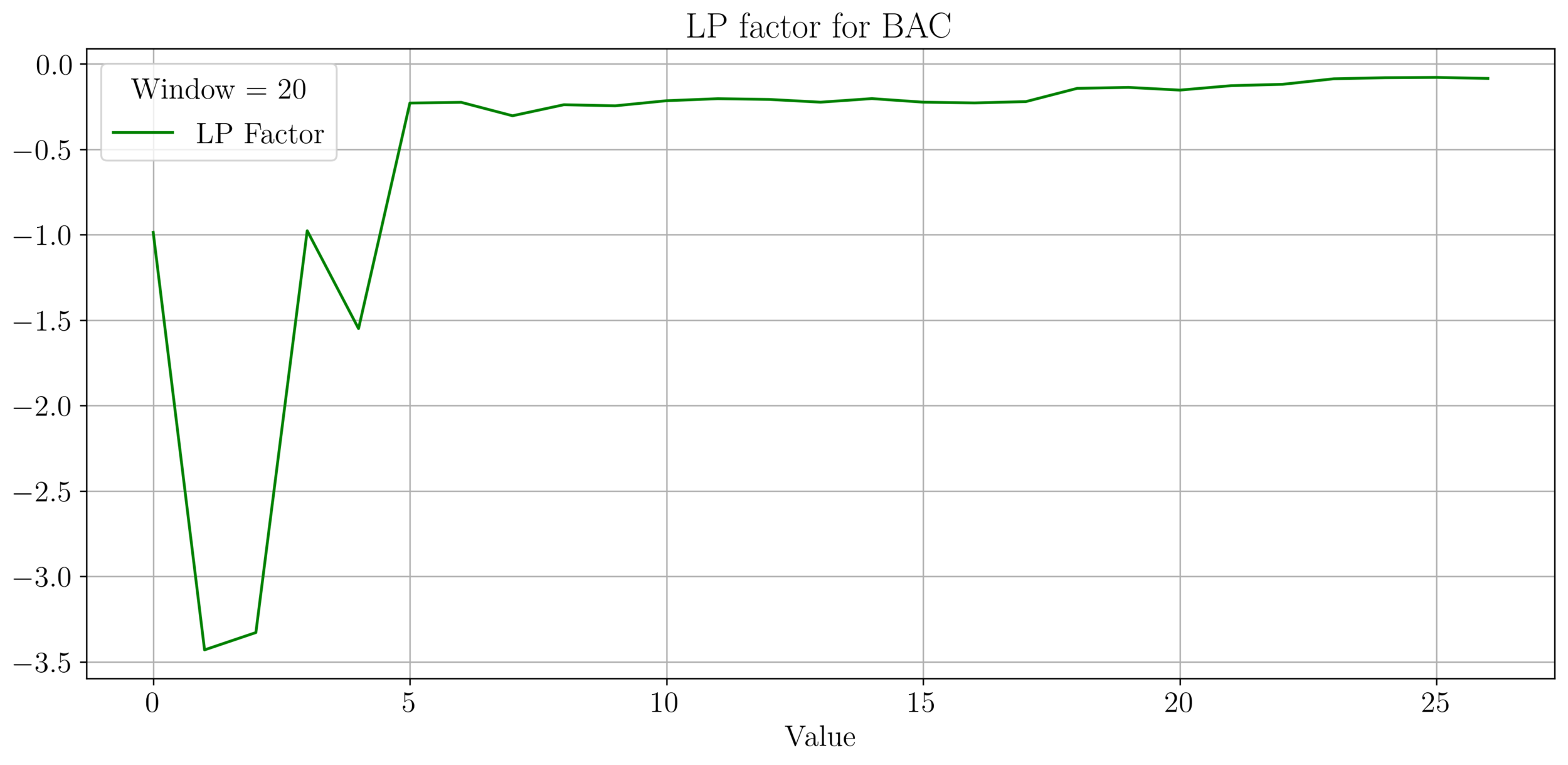
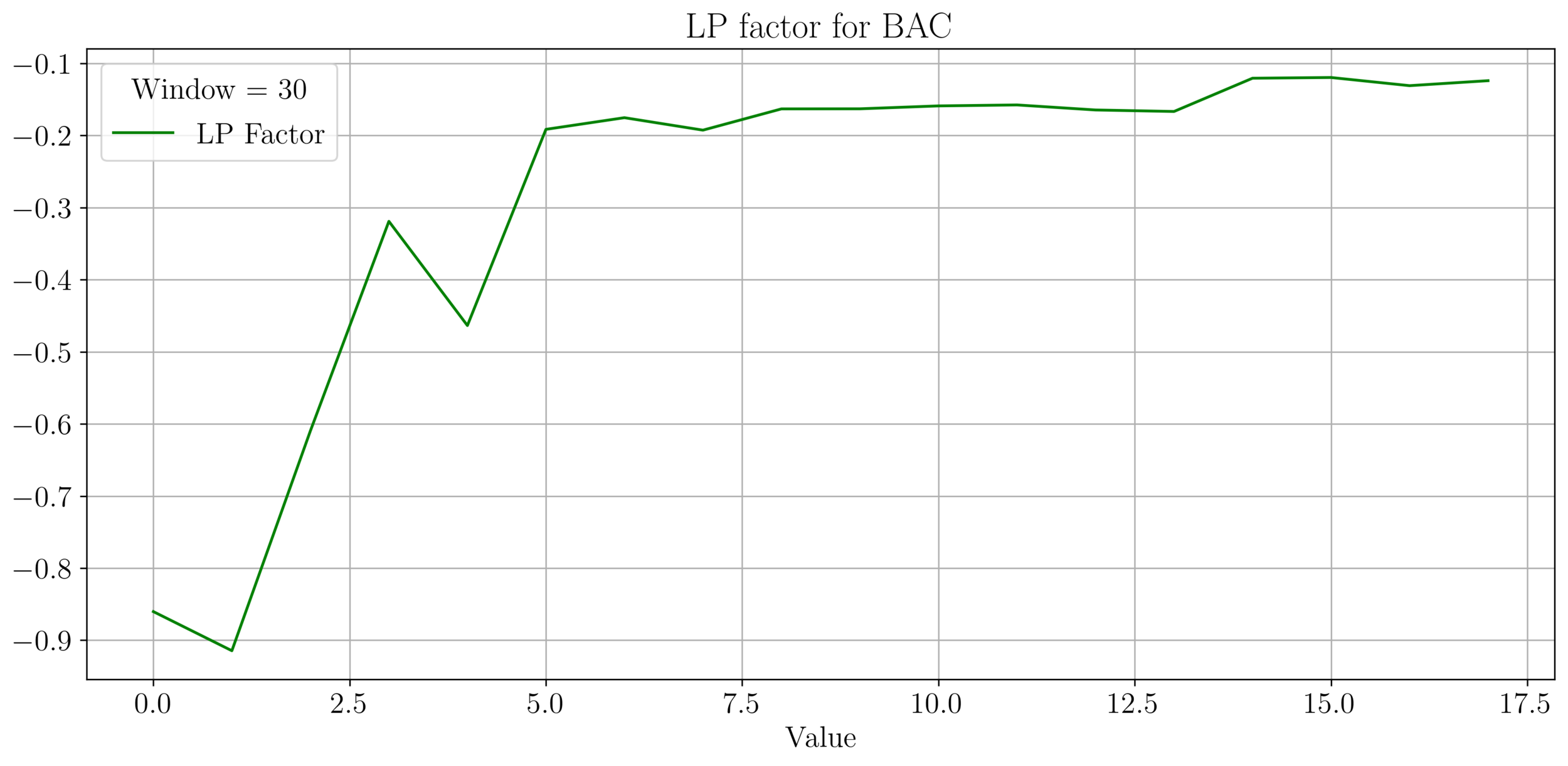
LP Wealth Factor
- We plot the factor \(f = \frac{\sigma^2}{2\mu}\), for max LP wealth growth, we want \(f \in (0.66, 2)\).
- We observe an irregular pattern here, need more investigation on this.