LP Wealth Growth in Uniswap

Preliminaries

\(X_t, Y_t \) are the quantities of numeraire and asset held by the LPs in the AMM
The price process of the asset is defined as \(S_0 = 1, S_t = S_{t-1}e^{\delta U_t}\)
\(\{U_i\}_{i \in \mathbb{N}}\) are i.i.d random variables s.t. \(\mathbb{P}[U_i = 1] = p, \ \mathbb{P}[U_i = -1] = 1-p\)
The implicit price given by the curve at time \(t\) is given by \(S_t^{\ast} = \frac{X_t}{Y_t}\)
Percentage fee: \((1 - \gamma)\), we constrain \(\gamma\) to be of the form \(e^{- k_{\gamma} \delta}, k_{\gamma} \in \mathbb{Z}\)
Trading equation \((X_t + \Delta X_t)^{\gamma} (Y_t - \Delta Y_t) = X_t^{\gamma} Y_t\)
Note that this is equivalent to \((X_t + \gamma\Delta X_t) (Y_t - \Delta Y_t) = X_t Y_t\)

\begin{aligned} \therefore \left(1 + \frac{\Delta X_t}{X_t}\right)^{\gamma} \left(1 - \frac{\Delta Y_t}{Y_t}\right) = 1 \quad &\implies \left(1 + \gamma\frac{\Delta X_t}{X_t}\right) \left(1 - \frac{\Delta Y_t}{Y_t}\right) = 1 \end{aligned}

\begin{aligned} \therefore (X_t + \gamma\Delta X_t) (Y_t - \Delta Y_t) &= X_t Y_t \end{aligned}

\begin{aligned} (X_t + \Delta X_t)^{\gamma} (Y_t - \Delta Y_t) &= X_t^{\gamma} Y_t \end{aligned}

Markov Chains

A stochastic model describing a sequence of possible events in which the probability of each event depends only on the current system state.
A discrete-time Markov chain is a sequence of random variables \(X_1, X_2, X_3, \ldots \) s.t.

\mathbb{P}\left(X_{n+1} = x \ | \ X_1 = x_1, X_2 = x_2, \dots, X_{n} = x_n\right) = \mathbb{P}\left(X_{n+1} = x \ | \ X_{n} = x_n\right)

Credits: https://setosa.io/ev/markov-chains/

Markov Chains

State space: \(S = \{A, B\}\), Transition matrix \(P \in \mathbb{R}_{[0, 1]}^{|S| \times |S|}\)
Stationary distribution: A probability distribution \(\pi = (p_A, p_B)\) that remains unchanged in the Markov chain as time progresses.

\pi P = \pi

Clearly, \(\pi\) is the left eigenvector of P for the eigenvalue \(\lambda = 1\).
For the above \(P\), we would have \(\pi = \left(\frac{5}{8}, \frac{3}{8}\right)\)

Implicit Price Manipulation

Suppose at time \(t\), we have \(S_t = \gamma^{-1}\left(\frac{X_t}{Y_t}\right) e^{\delta} = \gamma S_t^{\ast} e^{\delta}\)
We wish to bring the implicit price to \(S_{t+1}^{\ast} = \left(\frac{X_t}{Y_t}\right) e^{\delta}\) by trading \(\Delta Y_t\) for \(\Delta X_t\)
Thus, we have

\begin{aligned} \left(\frac{X_t + \Delta X_t}{Y_t - \Delta Y_t}\right) &= \left(\frac{X_t}{Y_t}\right) e^{\delta}\\[15pt] \quad (X_t + \Delta X_t)^{\gamma} (Y_t - \Delta Y_t) &= X_t^{\gamma} Y_t \end{aligned}

\begin{aligned} \implies \ \left(1 + \frac{\Delta X_t}{X_t}\right) = \left(1 - \frac{\Delta Y_t}{Y_t}\right) e^{\delta} \end{aligned}

\begin{aligned} \implies \ \left(1 + \frac{\Delta X_t}{X_t}\right)^{\gamma} \left(1 - \frac{\Delta Y_t}{Y_t}\right) = 1 \end{aligned}

\begin{aligned} \therefore \quad \Delta X_t = X_t\left(e^{\frac{\delta}{\gamma + 1}} - 1\right), \ \Delta Y_t = Y_t\left(1 - e^{\frac{-\gamma\delta}{\gamma + 1}}\right) \end{aligned}

Similarly, if \(S_t = \gamma \left(\frac{X_t}{Y_t}\right) e^{-\delta}\) and we pull the implicit price to \(S_{t+1}^{\ast} = \left(\frac{X_t}{Y_t}\right) e^{-\delta}\)

\begin{aligned} \therefore \quad \Delta X_t = X_t\left(1 - e^{\frac{-\gamma\delta}{\gamma + 1}}\right), \ \Delta Y_t = Y_t\left(e^{\frac{\delta}{\gamma + 1}} - 1\right) \end{aligned}

Price as Markov Process

Recall, we traded \(\Delta Y_t\) for \(\Delta X_t\) when \(S_t = \gamma^{-1} S_t^{\ast} e^{\delta} \implies S_t > \gamma^{-1} S_t^{\ast} \)
Similarly, we traded \(\Delta X_t\) for \(\Delta Y_t\) when \(S_t = \gamma S_t^{\ast} e^{-\delta} \implies S_t < \gamma S_t^{\ast} \)

Not profitable

Get \(\Delta Y_t\) for \(\Delta X_t\)

Get \(\Delta X_t\) for \(\Delta Y_t\)

\(0\)

\(\delta\)

\(-\delta\)

\(k_{\gamma}\delta\)

\(-k_{\gamma}\delta\)

\(\dots\)

\(k_{\gamma}\delta+\delta\)

\(-k_{\gamma}\delta-\delta\)

\text{log}\left(\frac{S_t}{S_t^{\ast}}\right)

Thus, \(M_t = \text{log}\left(\frac{S_t}{S_t^{\ast}}\right)\) is a Markov process with \(S = \{-k_{\gamma}\delta, \dots, -1, 0, 1, \dots, k_{\gamma}\delta\}\).
A trade occurs when \(M_t\) stays on one of the two end states.
Let's construct the transition matrix \(P\) and find a stationary distribution \(\pi\)

Price as Markov Process

Let's construct the transition matrix \(P\) and find a stationary distribution \(\pi\)

\(-k_{\gamma}\delta\)

\(-k_{\gamma}\delta + \delta\)

\(-k_{\gamma}\delta\)

\(\ldots\)

\(k_{\gamma}\delta\)

\(\ldots\)

\(-k_{\gamma}\delta + 2\delta\)

\(1-p\)

\(p\)

\(0\)

\(1-p\)

\(p\)

\(1-p\)

\(p\)

\(0\)

\(p\)

\(0\)

\text{log}\left(\frac{S_t}{S_t^{\ast}}\right)

\pi = \begin{cases} \left[ (2k_{\gamma} + 1)^{-1}, \dots, (2k_{\gamma} + 1)^{-1} \right] & \text{if } p = 0.5 \\[5pt] \left[ \frac{(1 - c)}{c^{-(2k_{\gamma}+1)} - 1}, \frac{(1 - c)c^{-1}}{c^{-(2k_{\gamma}+1)} - 1}, \frac{(1 - c)c^{-(2k_{\gamma} + 1)}}{c^{-(2k_{\gamma}+1)} - 1} \right] & \text{if } p \in (0.5,1], \ c = \frac{1-p}{p} \end{cases}

Constant Growth of Invariant

\begin{aligned} K_{\gamma} &= \frac{(X + \Delta X_t)(Y - \Delta Y_t)}{X_t Y_t} \\[5pt] &= \left(\frac{X + \Delta X_t}{X_t}\right)^{1 - \gamma} \frac{(X + \Delta X_t)^{\gamma}(Y - \Delta Y_t)}{X_t^{\gamma} Y_t} \\[5pt] &= \left(1 + \frac{\Delta X_t}{X_t}\right)^{1 - \gamma} = e^{\delta \frac{1 - \gamma}{1 + \gamma}} \end{aligned}

After each trade the product \(C_t = X_tY_t\) is increased by the same factor \(K_{\gamma}\)

If \(N_t\) trades occur until time \(t\), the wealth in the AMM at time \(t\) in the absence of fees is

\begin{aligned} K_{\gamma}^{-\frac{N_t}{2}} (Y_t S_t^{\ast} + X_t) &= (X_t Y_t)^{-\frac{1}{2}} (Y_t S_t^{\ast} + X_t) = 2 (X_t Y_t)^{-\frac{1}{2}} Y_t = 2 (S_t^{\ast})^{\frac{1}{2}} \end{aligned}

Expected Geometric Return for LPs

\begin{aligned} \mathbb{E}(\text{log} \ W_t) &= \mathbb{E}(\text{log} (Y_tS_t + X_t)) \\ &= \mathbb{E}(\text{log} (Y_tS^{\ast}_t + X_t)) + \mathbb{E}\left(\text{log} \left(\frac{Y_tS_t + X_t}{Y_tS^{\ast}_t + X_t}\right)\right) \end{aligned}

The wealth of LPs at time \(t\) is given as \(W_t = Y_t S_t + X_t\). Expected wealth is

\begin{aligned} \gamma \le \frac{S_t}{S^{\ast}_t} \le \gamma^{-1} \implies \gamma \le \left(\frac{Y_tS_t + X_t}{Y_tS^{\ast}_t + X_t}\right) \le \gamma^{-1} \end{aligned}

But we have,

\(m\) (constant)

\begin{aligned} \therefore \ \mathbb{E}(\text{log} \ W_t) &= \mathbb{E}(\text{log} (Y_tS^{\ast}_t + X_t)) + m \end{aligned}

\(\because \ K_{\gamma}^{-\frac{N_t}{2}}(Y_t S_t^{\ast} + X_t) = 2(S_t^{\ast})^{\frac{1}{2}} \)

\begin{aligned} = \mathbb{E}\left( \text{log} K_{\gamma}^{\frac{N_t}{2}} + \frac{1}{2}\text{log} S_t^{\ast}\right) + m \end{aligned}

\begin{aligned} = \left(\frac{\text{log} K_{\gamma}}{2}\right) \mathbb{E}(N_t) + \frac{1}{2} \mathbb{E}(\text{log} S_t^{\ast}) + m \end{aligned}

Asymptotic Geometric Return for LPs

\begin{aligned} \therefore \ \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} \ W_t)}{t} \end{aligned}

\begin{aligned} = \left(\frac{\text{log} K_{\gamma}}{2}\right) \lim_{t\to\infty} \frac{\mathbb{E}(N_t)}{t} + \frac{1}{2} \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} S_t^{\ast})}{t} \end{aligned}

\begin{aligned} (1 - p)(-\delta) + p\delta = \delta(2p-1) \end{aligned}

Average number of trades during an interval of time while in the stationary distribution of the Markov chain.

Let \(\pi = \left[\pi(-k_{\gamma}\delta), \dots, \pi(-k_{\gamma}\delta) \right]\)

\(\mathbb{E}(N_t) = nt [(1 - p)\pi(-k_{\gamma}\delta) + p\pi(k_{\gamma}\delta)]\), \(\frac{1}{n}\) is the time interval

\begin{aligned} \therefore \ \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} \ W_t)}{t} \end{aligned}

\begin{aligned} = \left(\frac{\text{log} K_{\gamma}}{2}\right) n[(1 - p)\pi(-k_{\gamma}\delta) + p\pi(k_{\gamma}\delta)] + \frac{n\delta(2p-1)}{2} \end{aligned}

Therefore, we finally have a closed form expression for the wealth growth of LPs!

Understanding Volatility Drag

Suyash Bagad

Geometric Brownian Motion

Stock prices in traditional finance are modeled using GBM

\begin{aligned} \frac{\Delta S_t}{S_t} = \mu \Delta t + \sigma \sqrt{\Delta t} \varepsilon \end{aligned}

\(\mu \Delta t\) - the expected returns of the stock
\(\sigma \sqrt{\Delta t} \varepsilon\) - models the random fluctuations of the stock price
On solving the above SDE, we note that \(S_t\) is log-normally distributed

\begin{aligned} \text{log}\left(\frac{ S_t}{S_0}\right) \sim \mathcal{N}\left(\left(\mu - \frac{\sigma^2}{2}\right)t , \sigma \sqrt{t}\right) \end{aligned}

Volatility

Random process

Markov process

Drift

Price Process as a GBM

For the price process \(S_t\) of the asset \(Y_t\), we have

Mean: \(\mathbb{E}(\text{log}(S_t)) = \delta p + (-\delta)(1 - p) = \delta(2p-1)\)
Variance: \(\mathbb{V}(\text{log}(S_t)) = \mathbb{E}((\text{log}(S_t))^2) - (\mathbb{E}(\text{log}(S_t)))^2 = \delta^2 - \delta^2(2p-1)^2 = 4\delta^2 p(1-p)\)
Let us assume that \(\delta\) depends on \(\Delta t = \frac{1}{n}\). For \(S_t\) to be GBM, we must have

S_t = \begin{cases} S_{t-1}e^{\delta} & \text{with probability } p \\ S_{t-1}e^{-\delta} & \text{with probability } (1-p) \end{cases}

\begin{aligned} \delta_n (2p_n - 1) &= \left(\mu - \frac{\sigma^2}{2} \right)\frac{1}{n} \\ 2\delta_n \sqrt{p(1-p)} &= \frac{\sigma}{\sqrt{n}} \end{aligned}

Thus, we get \(\delta_n \approx \frac{\sigma}{\sqrt{n}}\) and \(p_n \approx \frac{1}{2} + \frac{d}{2\sigma \sqrt{n}} \) where \(d = \left(\mu - \frac{\sigma^2}{2} \right)\).

LP Wealth Growth

For a time interval \(\Delta_t = \frac{1}{n}\) and let \(a = \frac{1-p}{p}\), the growth rate of LP wealth is

\begin{aligned} \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} \ W_t)}{t} = \begin{cases} \frac{n\delta}{2} \frac{1}{1 - 2 \frac{\text{log}\gamma}{\delta}} \left(\frac{1 - \gamma}{1 + \gamma}\right) & p = \frac{1}{2} \\[10pt] \frac{n\delta(2p-1)}{2} \left(\frac{1 \ - \ a \gamma^{-\frac{2}{\delta}\text{log}(a)}}{1 \ + \ a \gamma^{-\frac{2}{\delta}\text{log}(a)}} \left(\frac{1 - \gamma}{1 + \gamma}\right) + 1\right) & p > \frac{1}{2} \end{cases} \end{aligned}

The wealth of LP at time \(t\), given by \(W_t = X_t + S_t Y_t\)
The factor by which the price \(S_t\) can change
Fee percentage \(1 - \gamma\), note that \(\gamma \rightarrow 1\)
Substituting \((p_n, \delta_n)\) from previous slide, we can obtain LP wealth growth for a continuous case.

Case I: \(p = \frac{1}{2} \implies d = 0\). Substituting \(\delta_n = \frac{\sigma}{\sqrt{n}}\) for \(n \rightarrow \infty\)

Convergence to Continuity

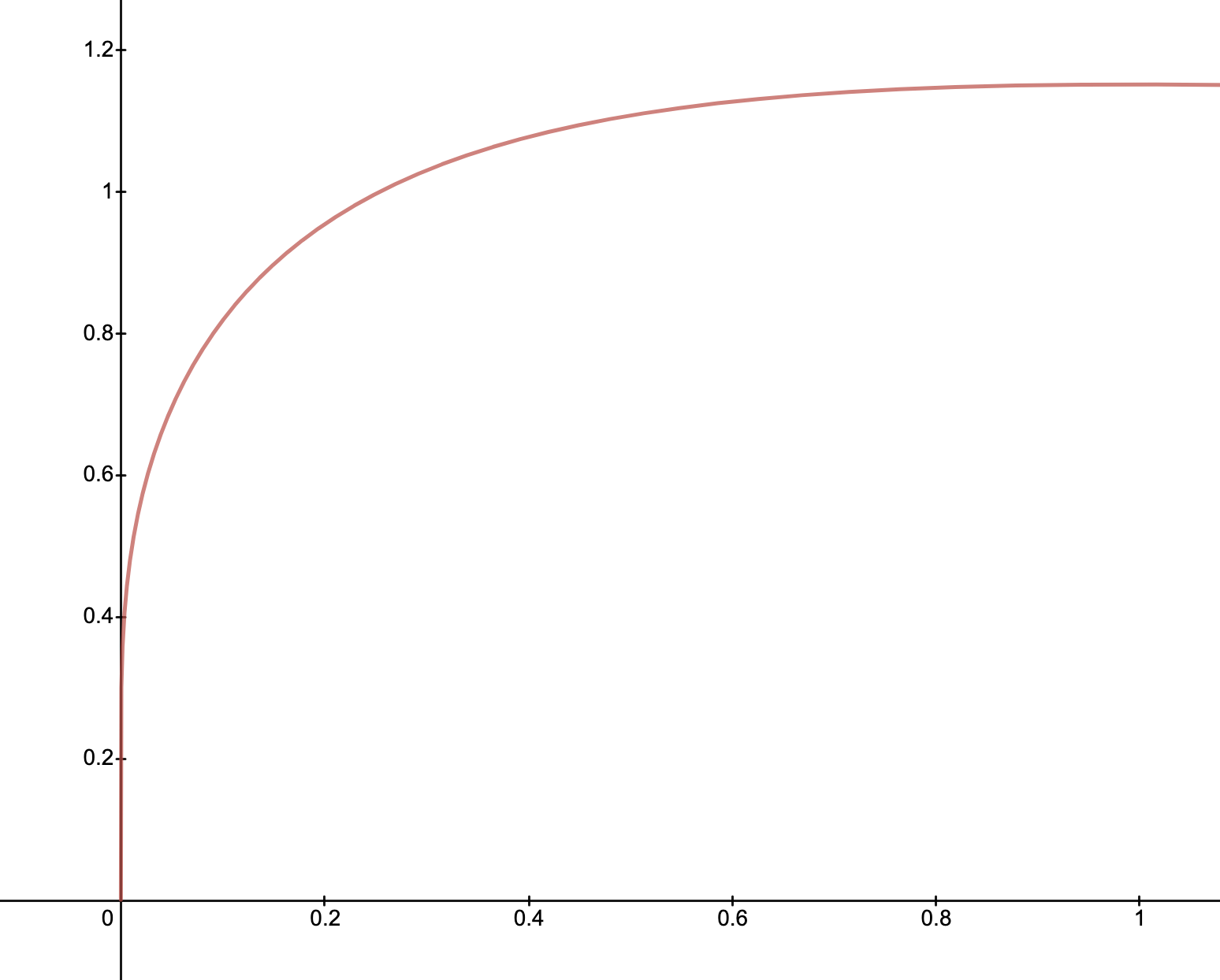
\begin{aligned} \lim_{n\to\infty} \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} \ W_t)}{t} &= \lim_{n\to\infty} \frac{\sigma\sqrt{n}}{2} \frac{1}{1 - 2 \sqrt{n} \frac{\text{log}\gamma}{\sigma}} \left(\frac{1 - \gamma}{1 + \gamma}\right) = -\frac{\sigma^2}{4\text{log}(\gamma)} \left(\frac{1 - \gamma}{1 + \gamma}\right) \end{aligned}

-\frac{1}{\text{log}(\gamma)} \left(\frac{1 - \gamma}{1 + \gamma}\right)

The LP wealth increases in \(\gamma \in [0,1]\)
For \(\gamma \rightarrow 1\), the return is

\begin{aligned} \lim_{\gamma\to1} -\frac{\sigma^2}{4\text{log}(\gamma)} \left(\frac{1 - \gamma}{1 + \gamma}\right) = \frac{\sigma^2}{8} \end{aligned}

The un-rebalanced portfolio is zero!

Convergence to Continuity

\begin{aligned} \lim_{n\to\infty} \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} \ W_t)}{t} &= \frac{d}{2} \left( \left( \frac{1 + \gamma^{\frac{4d}{\sigma^2}}}{1 - \gamma^{\frac{4d}{\sigma^2}}} \right) \left(\frac{1 - \gamma}{1 + \gamma}\right) + 1 \right) \end{aligned}

Case II: \(p > \frac{1}{2}\). Substituting \(p_n\) and \(\delta_n\)

The LP wealth decreases in \(\gamma \in [0,1]\) if \(4d > \sigma^2\). \(\gamma \rightarrow 0\) gives best possible growth \(d\).
The wealth increases in \(\gamma \in [0,1]\) if \(4d < \sigma^2\). \(\gamma \rightarrow 1\) gives best growth \(\frac{d}{2} + \frac{\sigma^2}{8}\).

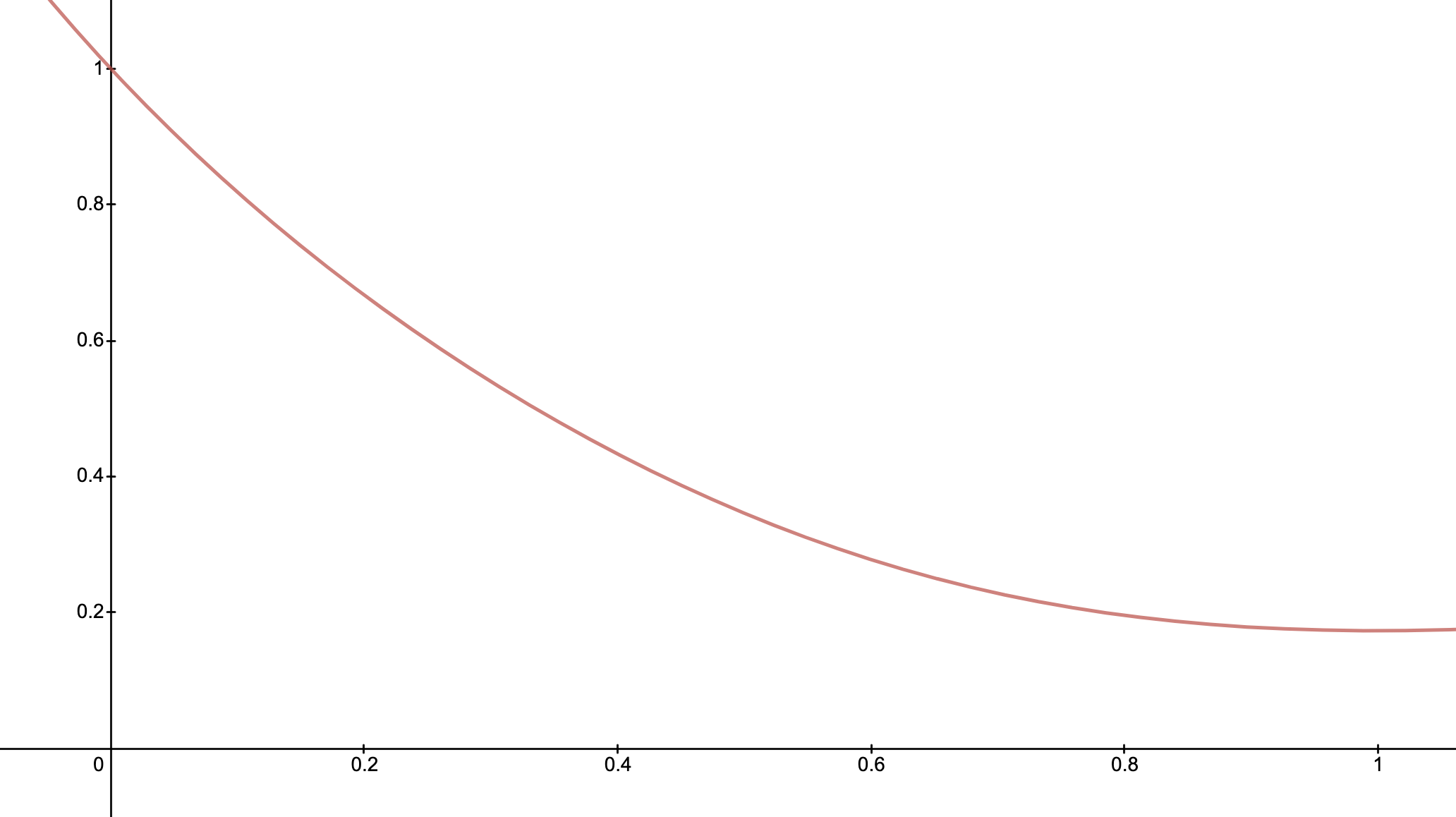
\begin{aligned} \left( \frac{1 + \gamma^{\frac{4d}{\sigma^2}}}{1 - \gamma^{\frac{4d}{\sigma^2}}} \right) \left(\frac{1 - \gamma}{1 + \gamma}\right) \end{aligned}

\(\frac{4d}{\sigma^2} > 1\)

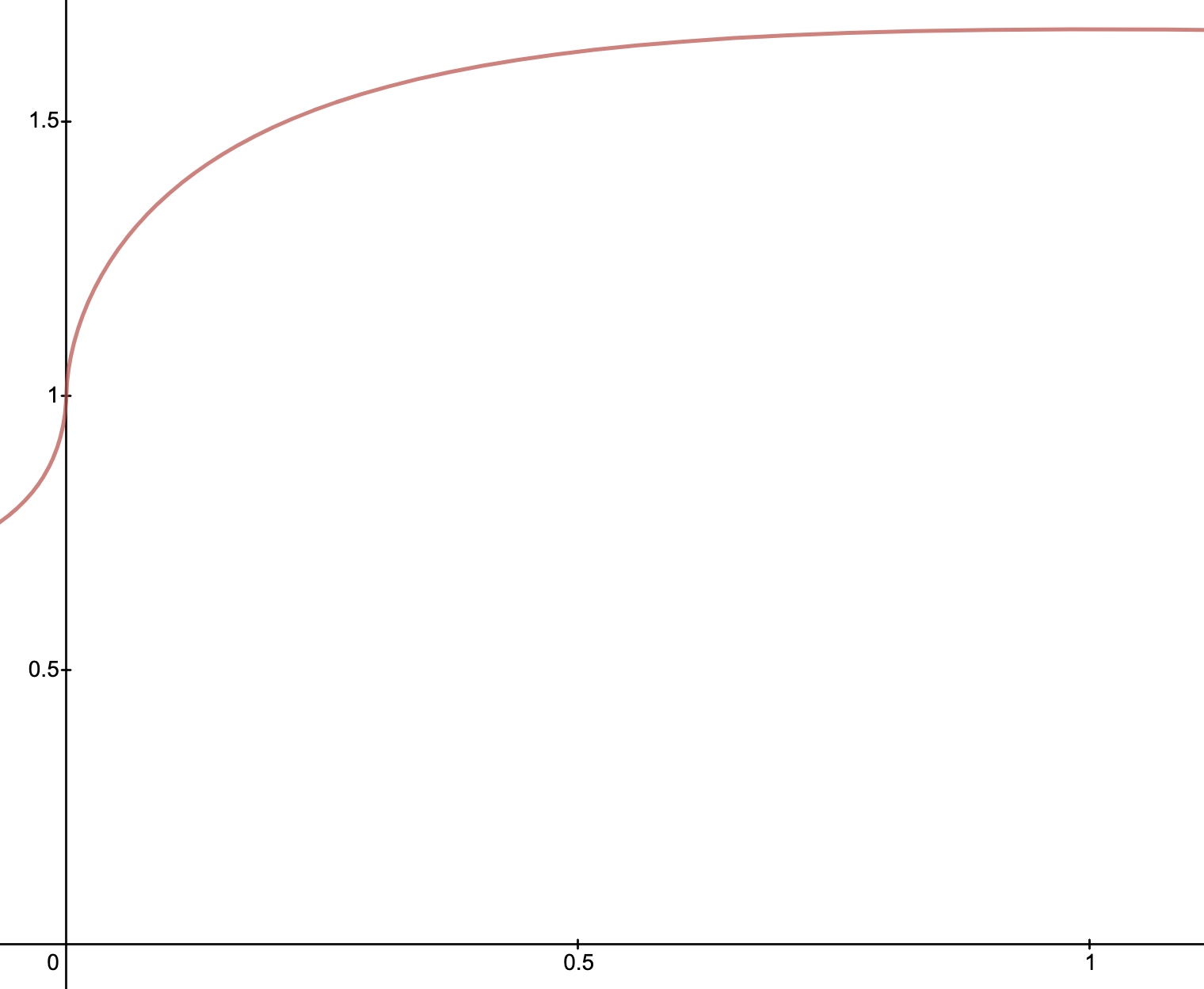
\(\frac{4d}{\sigma^2} < 1\)

Summary

\(p = \frac{1}{2}\)

\(p > \frac{1}{2}\)

HOLDers

LPs

\(0\)

\(\mu - \frac{\sigma^2}{2}\)

\(3\sigma^{2}> 4\mu\)

\(3\sigma^{2} < 4\mu\)

\(\frac{\sigma^2}{8}\)

\(\frac{1}{2}\left(\mu - \frac{\sigma^2}{4}\right)\)

\(3\sigma^{2}= 4\mu\)

\(\mu - \frac{\sigma^2}{2}\)

Therefore, LPs always do either equal or better than HODLers!
For LPs to always do better, we must that: \(3\sigma^2 > 4\mu\) and \(\mu > \frac{\sigma^2}{4}\). Thus,

\begin{aligned} \frac{4\mu}{3} < \sigma^2 < 4\mu \ \implies \ \frac{2}{3} < \frac{\sigma^2/2}{\mu} < 2 \end{aligned}

Volatility Drag

When \(p > 0.5\), the expected growth rate of the price of the asset is

\begin{aligned} G_{\text{HODL}} = \mu - \frac{\sigma^2}{2} \end{aligned}

Here the term \(-\frac{\sigma^2}{2}\) is known as the volatility drag.
In the same case of \(p > 0.5\), if we have \(\frac{2\sqrt{\mu}}{\sqrt{3}} < \sigma < 2\sqrt{\mu},\) we have

\begin{aligned} G_{\text{LP}} = \frac{1}{2}\left(\mu - \frac{\sigma^2}{4}\right) > G_{\text{HODL}} \end{aligned}

Within that range, being a Uniswap LP will eventually make you rich, and in fact richer than you could become by holding any unrebalanced portfolio consisting of cash and the asset.

- LP Wealth paper Authors