Basic Graph
什麼是圖論?
千里之行始於足下
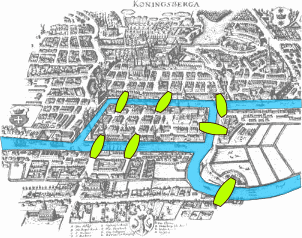
七橋問題:
如果上圖每一座橋都只能經過一次,
是否存在一種方法走遍這 7 座橋
圖的定義
- 一個圖 Graph 由
- 一些頂點 Vertices
- 連接兩頂點的邊 Edges
構成
-
邊可能有方向
-
如果所有邊都沒有標記方向
則稱之為 無向圖
-
如果有方向規定,則為有向圖
- 無向圖相當於所有邊都雙向通行的有向圖
-
如果所有邊都沒有標記方向

B
C
A
D
A
B
A
B
圖論:討論點邊關係的學問
圖的定義
- 一個圖 Graph 由
- 一些頂點 Vertices
- 連接兩頂點的邊 Edges
構成
- 邊可能有方向
- 如果所有邊都沒有標記方向
則稱之為 無向圖
- 如果有方向規定,則為有向圖
- 無向圖相當於所有邊都雙向通行的有向圖
- 如果所有邊都沒有標記方向

B
C
A
D
A
B
A
B
圖的定義

B
C
A
D
點的 度數 (degree)
一個點 \(v\) 被幾條邊連接
左圖中
\(\deg(A) = 3\)
\(\deg(B) = 5\)
圖的定義

B
C
A
D
點的 有向度數 (directed degree)
出度 Out degree 是一個點 \(v\) 伸出幾條邊
入度 In degree 是一個點 \(v\) 有多少邊指向他
A
B
\(\deg_{in}(A)=0\)
\(\deg_{out}(A)=1\)
\(\deg_{in}(B)=1\)
\(\deg_{out}(B)=0\)
一筆畫問題

B
C
A
D
給定義一張連通無向圖,從一個頂點開始行走,是否存在一種方法
使得每條邊只經過一次的狀況下,
經過每一條邊
A
B
C
D
E
連通:任兩點都能透過邊互相抵達
一筆畫問題
A
B
C
D
E
- 把頂點分成兩類:
- 起點 / 終點
- 其他
如果頂點 \(v_x\) 不是起點也不是終點
若要能一筆畫
那 \(\deg(v_x)\) 一定要是偶數 (why?)
\(\Rightarrow\) 最多只有兩個點的 degree 是奇數,分別為起點與終點
\(\Rightarrow\) 如果沒有頂點 degree 是奇數,每個點都能當起點 (起點與終點是同一個點)
note. 不存在 只有 \(1\) 個點的 degree 是奇數的圖 (why?)
練習
zerojudge
b924: kevin 愛畫畫
Hint
- 圖論題目,要檢查
- 邊有沒有方向
- 圖是不是連通的
極大部分的圖論題目輸入都長這樣
V E // 幾個點, 幾個邊
// 接下來有 E 行
v1 v2 // v1 v2 之間有邊
...
...
...
vn vm輸入通常很大,要注意 IO 時間
#include <bits/stdc++.h>
using namespace std;
int deg[10001];
int main() {
int N, M;
scanf("%d%d", &N, &M);
while (M--) {
int a, b;
scanf("%d%d", &a, &b);
deg[a]++;
deg[b]++;
}
int odds = 0;
for(int i=1;i<=N;++i)
if (deg[i]%2==1)
odds ++;
if (odds > 2) cout <<"NO\n";
else cout <<"YES\n";
}
圖的走訪
連通性 (Connectivity)
- 一張圖中,如果一個點 \(a\) 可以透過一些邊走到 \(b\),就說
存在路徑 (walk) \(a\) 到 \(b\)
A
B
C
D
E
無向圖中,如果 \(a\) 能到 \(b\),那 \(b\) 也能到 \(a\)
有向圖則不一定
連通圖
- 如果一個無向圖任兩點之間都有路徑相連,那這一張圖就是連通圖
A
B
C
D
A
B
C
D
連通
不連通
連通圖判定
- 給定一個無向圖,請輸出他是不是連通圖
A
B
C
D
A
B
C
D
連通
不連通
連通的性質
對於一個無向圖
- 如果 \(a\) 與 \(b\) 連通,那 \(b\) 與 \(a\) 也連通
- 如果 \(a\) 與 \(b\) 連通, \(a\) 與 \(c\) 連通,那 \(b\) 與 \(c\) 也連通
A
B
C
D
連通
因此檢查一張圖是否連通
只需要選擇隨意的一個起點
看看能不能由起點走到其他所有的頂點就行了
圖的紀錄方法
- 為了讓演算法能夠方便運作,需要選擇適當的方法來記錄點與邊
- 常見有三種方法
- 鄰接矩陣
- 鄰接串列
- 邊陣列
最常使用的為第二種 - 鄰接串列
每種都有不同的使用情境,會在遇到時介紹
使用情境出現位置 : 鄰接矩陣 : 全點對最短路徑、圖論的數學計算 / 邊陣列 : 最小生成樹、網路流
鄰接串列
對於每一個點 \(v\),用一個 vector 紀錄他的鄰居有誰
A
B
C
D
vec[A] = {B, C}
vec[B] = {A, C}
vec[C] = {A, B, D}
vec[D] = {C}vector : C++ 內建可以自動長大的陣列 @
vector<int> V[100];
// 輸入一條邊
cin >> s >> e;
// s 的鄰居們加入 e
V[s].empalce_back(e);
// 無向圖中要記得反過來的路也要蓋!
V[e].empalce_back(s);圖的走訪 - 迴圈版
- 從一個起點出發,找到所有可以透過邊走到的所有點 !
Key point : 用一個陣列紀錄有哪一些點我們可以用
vector<int> todo; // 紀錄有那一些點等待我們去走
todo.emplace_back(S); // 一開始只知道起點 !圖的走訪 - 迴圈版 (有bug)
vector<int> todo; // 紀錄有那一些點等待我們去走
todo.emplace_back(S); // 一開始只知道起點 !
while (!todo.empty()) // 如果還有點沒有去看他
{
int v = todo.back(); // 挑一個的資料出來
todo.pop_back(); // 拿出來的記得刪掉!
for(int u:V[v]) // 找 v 的所有鄰居
todo.emplace_back(u); // 放到清單中
}透過一個點的鄰居,可以讓我們知道還有哪一些點沒有被走過!
A
B
C
A->B->C->A->B->C...
無窮迴圈 !?
圖的走訪 - 迴圈版
vector<int> todo;
vector<bool> used(V); // 紀錄一個點有沒有被走過
todo.emplace_back(S);
used[S] = true;
while (!todo.empty())
{
int v = todo.back();
todo.pop_back();
for(int u:V[v])
if (!used[u]) { // 如果 u 還沒看過
todo.emplace_back(u);
used[u] = true; // 紀錄為已看過
}
}一個點只要被看過一次,要再用一個陣列紀錄有沒有看過
不然會有無窮迴圈的問題 !
A
B
C
D
起點 : A
todo = {A}
A
B
C
D
起點 : A
todo = {}
拿出 A
A
B
C
D
起點 : A
todo = {B,C}
拿出 A
把 A 的鄰居放到 todo
A
B
C
D
起點 : A
todo = {B}
拿出 A
把 A 的鄰居放到 todo
拿出 C
Question : 第三步可以改拿 B 嗎 ?
A
B
C
D
起點 : A
todo = {B,D}
拿出 A
把 A 的鄰居放到 todo
拿出 C
把 C 的鄰居放到 todo
A
B
C
D
起點 : A
todo = {B}
拿出 A
把 A 的鄰居放到 todo
拿出 C
把 C 的鄰居放到 todo
拿出 D
A
B
C
D
起點 : A
todo = {B}
拿出 A
把 A 的鄰居放到 todo
拿出 C
把 C 的鄰居放到 todo
拿出 D
把 D 的鄰居放到 todo
A
B
C
D
起點 : A
todo = {}
拿出 A
把 A 的鄰居放到 todo
拿出 C
把 C 的鄰居放到 todo
拿出 D
把 D 的鄰居放到 todo
拿出 B
A
B
C
D
起點 : A
todo = {}
拿出 A
把 A 的鄰居放到 todo
拿出 C
把 C 的鄰居放到 todo
拿出 D
把 D 的鄰居放到 todo
拿出 B
把 B 的鄰居放到 todo
A
B
C
D
起點 : A
todo = {}
拿出 A
把 A 的鄰居放到 todo
拿出 C
把 C 的鄰居放到 todo
拿出 D
把 D 的鄰居放到 todo
拿出 B
把 B 的鄰居放到 todo
todo 沒東西了,演算法結束
我們找出了所有從起點 A 出發能到達的點!
練習題
- ZJ a290 新手訓練系列 ~ 圖論
#include <bits/stdc++.h>
using namespace std;
vector<int> V[801];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int N, M;
while (~scanf("%d%d", &N, &M))
{
for(int i=1;i<=N;++i)
V[i].clear();
while (M--)
{
int a, b;
scanf("%d%d", &a, &b);
V[a].emplace_back(b);
}
int S, E;
scanf("%d%d", &S, &E);
vector<int> todo;
vector<int> used(N+1);
todo.emplace_back(S);
used[S] = true;
while (!todo.empty()) {
int v = todo.back();
todo.pop_back();
for(int u:V[v])
if (!used[u]) {
used[u] = true;
todo.emplace_back(u);
}
}
if (used[E]) cout << "Yes!!!\n";
else cout << "No!!!\n";
}
}
圖的走訪 - 遞迴版
透過遞迴不斷的往前行走,來找到所有可以到達的點 !
void dfs(int v) { // 現在走到 v 號點
used[v] = true; // 走過了一樣要標記!
}圖的走訪 - 遞迴版
透過遞迴不斷的往前行走,來找到所有可以到達的點 !
void dfs(int v) { // 現在走到 v 號點
used[v] = true; // 走過了一樣要標記!
for (int u:V[v]) // 看 v 的所有鄰居
if (!used[u]) // 如果沒走過
dfs(u); // 去看看他
}試著改寫前面的程式碼~
#include <bits/stdc++.h>
using namespace std;
vector<int> V[801];
bool used[801];
void dfs(int v) {
used[v] = true;
for (int u:V[v])
if (!used[u])
dfs(u);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int N, M;
while (~scanf("%d%d", &N, &M))
{
for(int i=1;i<=N;++i) {
V[i].clear();
used[i] = false;
}
while (M--)
{
int a, b;
scanf("%d%d", &a, &b);
V[a].emplace_back(b);
}
int S, E;
scanf("%d%d", &S, &E);
dfs(S);
if (used[E]) cout << "Yes!!!\n";
else cout << "No!!!\n";
}
}
迴圈 vs 遞迴
- 迴圈寫起來程式碼比較長
- 迴圈容易改寫成不同形式的搜尋
- 遞迴程式碼精簡
- 搜尋方法較單純
實務上兩種方法都會用到,都要學
練習題
UVa 10004 Bicoloring
給一張圖,問可不可以剛好用兩種顏色圖滿整張圖,使得相鄰不同色
網格圖的走訪技巧
練習題
ZJ b689: 2. 棕櫚迷宮
根據題目的變化,圖不一定要是普通的點線
也可能是用陣列 "畫出來" 的

練習題
ZJ b689: 2. 棕櫚迷宮
根據題目的變化,圖不一定要是普通的點線
也可能是用陣列 "畫出來" 的

網格圖
我們通常把這種座標轉換的圖稱之為網格圖
網格圖通常可以利用座標當作點的編號,來做圖論的處理
不需要轉換為一般圖的形式

網格圖走訪 - 迴圈

把之前得程式碼做一點修改 ! 使用座標當作點的編號
char map[50][50]; // 把地圖存在 char 陣列裡面
int H, W; // 地圖長寬
int x, y;
// x,y = 找到的入口座標
vector<tuple<int,int>> todo;
todo.emplace_back(x, y);Tuple : 合併資料儲存 @
網格圖走訪 - 迴圈
一個座標 (x,y) 的鄰居有誰 ?
vector<tuple<int,int>> todo;
bool used[100][100]; // 直接用二維陣列紀錄有沒有用過
todo.emplace_back(x, y);
used[x][y] = true;
while (!todo.empty()) {
tie(x, y) = todo.back();
todo.pop_back();
// 找 (x, y) 的鄰居
}(x+1,y) (x-1,y) (x,y+1) (x,y-1)
要怎麼快速地列出鄰居 ?
列舉 4 / 8 方向
- 把座標的差用陣列儲存起來
- 就能用迴圈枚舉了 !
int dx[] = {1,-1,0,0};
int dy[] = {0,0,1,-1};
{
for(int i=0;i<4;++i) {
int nx = x + dx[i];
int ny = y + dy[i];
}
}(x+1,y) (x-1,y) (x,y+1) (x,y-1)
千萬不要幹把程式碼複製 * n 的行為
程式碼越多越容易錯!
int dx[] = {-1, 0, 1,
-1, 1,
-1, 0, 1};
int dy[] ={-1,-1,-1,
0, 0,
1, 1, 1};while (!todo.empty()) {
tie(x, y) = todo.back();
todo.pop_back();
for (int i=0;i<4;++i) {
int nx = x+dx[i];
int ny = y+dy[i];
}
}
不是每一個格子上下左右都是鄰居!
有些是牆壁
有些超出地圖範圍
=> 判斷跳過
檢查是不是牆壁
檢查在不再地圖內
if (nx < 0 || H <= nx ||
ny < 0 || W <= ny)if (mp[nx][ny] == '#')哪一個要先判斷 ?
還是都可以 ?
陣列 :
永遠先檢查
要放到中括號裡的資料
檢查是不是牆壁
檢查在不在地圖內
for (int i=0;i<4;++i) {
int nx = x+dx[i];
int ny = y+dy[i];
if (nx < 0 || H <= nx ||
ny < 0 || W <= ny)
/* 這裡放什麼 */
if (mp[nx][ny] == '#')
/* 這裡放什麼 */
}if 的下面要放什麼 ?
提示 : 如果座標錯了,"跳過" 他
(A). break
(B). continue
(C). return
while (!todo.empty()) {
tie(x, y) = todo.back();
todo.pop_back();
for (int i=0;i<4;++i) {
int nx = x+dx[i];
int ny = y+dy[i];
if (nx < 0 || H <= nx ||
ny < 0 || W <= ny)
continue;
if (mp[nx][ny] == '#')
continue;
if (!used[nx][ny]) {
todo.emplace_back(nx, ny);
used[nx][ny] = true;
}
}
}
// x,y 永遠記錄著最後從 todo 拿出的資料
// 題目座標從 1 開始的
cout << x+1 << ' ' << y+1 << '\n';
幾乎快完成了 !
題目要求 "最深" 的點
那大概就是最後放到 todo 的點吧
7 9
#########
##.....##
##.###.##
##.#...##
##.#.##..
#..#....#
#########
7 9
######.##
##.....##
##.####.#
##.#....#
##.#.##.#
#..#....#
#########
10 10
##########
#....#####
#.##.....#
#...####.#
#######..#
##....#.##
##.##.#..#
##.##.##.#
##..#....#
###.######
Testcases
幫你打好了
#include <bits/stdc++.h>
using namespace std;
int H, W;
char mp[50][50];
bool used[50][50];
tuple<int, int> findEntry(int h, int w) {
for (int i=0;i<h;++i) {
if (mp[i][0] == '.') return make_tuple(i,0);
if (mp[i][w-1] == '.') return make_tuple(i,w-1);
}
for (int i=0;i<w;++i) {
if (mp[0][i] == '.') return make_tuple(0,i);
if (mp[h-1][i] == '.') return make_tuple(h-1, i);
}
assert(false && "testcase error!");
}
int dx[] = {1,-1,0,0};
int dy[] = {0,0,1,-1};
int main()
{
cin >> H >> W;
for(int i=0;i<H;++i)
cin >> mp[i];
int x, y;
tie(x, y) = findEntry(H, W);
vector<tuple<int,int>> todo;
todo.emplace_back(x, y);
used[x][y] = true;
while (!todo.empty()) {
tie(x, y) = todo.back();
todo.pop_back();
for (int i=0;i<4;++i) {
int nx = x+dx[i];
int ny = y+dy[i];
if (nx < 0 || H <= nx ||
ny < 0 || W <= ny)
continue;
if (mp[nx][ny] == '#')
continue;
if (!used[nx][ny]) {
todo.emplace_back(nx, ny);
used[nx][ny] = true;
}
}
}
cout << x+1 << ' ' << y+1 << '\n';
}
試著改成遞迴版 !
- 跟迴圈幾乎一樣,不過沒有使用到 tuple
- 對於 tuple / vector 不熟的話,遞迴寫法較簡單
int ax, ay;
void dfs(int x, int y) {
used[x][y] = true;
// 暫存答案
ax = x;
ay = y;
for (int i=0;i<4;++i) {
int nx = x+dx[i];
int ny = y+dy[i];
if (nx < 0 || H <= nx ||
ny < 0 || W <= ny)
continue;
if (mp[nx][ny] == '#')
continue;
if (!used[nx][ny])
dfs(nx, ny);
}
}#include <bits/stdc++.h>
using namespace std;
int H, W;
char mp[50][50];
bool used[50][50];
tuple<int, int> findEntry(int h, int w) {
for (int i=0;i<h;++i) {
if (mp[i][0] == '.') return make_tuple(i,0);
if (mp[i][w-1] == '.') return make_tuple(i,w-1);
}
for (int i=0;i<w;++i) {
if (mp[0][i] == '.') return make_tuple(0,i);
if (mp[h-1][i] == '.') return make_tuple(h-1, i);
}
assert(false && "testcase error!");
}
int dx[] = {1,-1,0,0};
int dy[] = {0,0,1,-1};
int ax, ay;
void dfs(int x, int y) {
used[x][y] = true;
// 暫存答案
ax = x;
ay = y;
for (int i=0;i<4;++i) {
int nx = x+dx[i];
int ny = y+dy[i];
if (nx < 0 || H <= nx ||
ny < 0 || W <= ny)
continue;
if (mp[nx][ny] == '#')
continue;
if (!used[nx][ny])
dfs(nx, ny);
}
}
int main()
{
cin >> H >> W;
for(int i=0;i<H;++i)
cin >> mp[i];
int x, y;
tie(x, y) = findEntry(H, W);
dfs(x, y);
cout << ax+1 << ' ' << ay+1 << '\n';
}
深度優先搜尋
Depth-First-Search
總是拿 "最新發現的鄰居" 來考慮
是一切搜尋最基本的方法
void dfs(int v) {
used[v] = true;
for (int u: V[v]) {
if (!used[u]) {
// 一發現新鄰居,立刻走上去
dfs(u);
}
}
}while (!todo.empty()) {
v = todo.back(); // 拿最後的東西
for (int u: V[v]) {
if (!used[u]) {
// 一發現新鄰居,放到 todo 最後面
dfs(u);
used[u] = true;
}
}
}額外練習
c129: 00572 - Oil Deposits (簡單網格圖)
d768: 10004 - Bicoloring (hint: 邊走路邊圖顏色)
b517 : 是否為樹-商競103 (hint : 一個圖為樹 => 連通 且 沒有環)
A
B
C
D
樹
A
B
C
D
不是樹
(ABC形成循環)
A
B
C
D
不是樹
(不連通)
b517 參考輸入範例
這一題雖然簡單,但細節有點多
輸入也對初學者不太友善
可以複製左邊程式碼來繼續寫
程式碼已經寫到把圖建立好的程度了
#include <bits/stdc++.h>
using namespace std;
vector<int> V[81];
int used[81];
bool appeared[81];
int main() {
int T;
cin >> T; cin.get();
while (T--) {
string buf;
getline(cin, buf);
// 初始化放這裡
memset(used, 0, sizeof(used));
memset(appeared, 0, sizeof(appeared));
for(int i=0;i<81;++i) V[i].clear();
int x, y;
stringstream ss(buf);
while (ss >> buf) {
sscanf(buf.c_str(), "%d,%d", &x, &y);
// 讀取一條邊 x<=>y
appeared[x] = appeared[y] = true;
V[x].emplace_back(y);
V[y].emplace_back(x);
}
// 繼續做你想做的事情
}
}邊最短距離
邊最短距離
- DFS 是依照有路就先走的方法來找到資料的
- 但有的時候,我們會希望按照與起點距離,近到遠找資料
- 能求出每一個點距離起點幾條邊!
A
B
C
D
距離 0 : A
距離 1 : B, C
距離 2 : D
邊最短距離
- 之前的方法,我們總是拿最新發現的資料,這樣會讓搜尋的路優先往遠的方向走
- 其實,只要把原來的方法,改成用 "最舊" 的資料,就能由近到遠搜尋了
// 要把 vector<> todo 改成 deque<> todo
// deque 才能操作 front
while (!todo.empty()) {
v = todo.front(); // 拿前面的東西
todo.pop_front();
for (int u: V[v]) {
if (!used[u]) {
// 一發現新鄰居,放到 todo 最後面
todo.emplace_back(u);
used[u] = true;
}
}
}A
B
C
D
起點 : A
todo = {A}
0
A
B
C
D
起點 : A
todo = {}
拿出 A
0
A
B
C
D
起點 : A
todo = {}
拿出 A
把 A 的鄰居距離設定為自己+1
0
1
1
A
B
C
D
起點 : A
todo = {B,C}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
0
1
1
A
B
C
D
起點 : A
todo = {C}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
拿出 B
0
1
1
A
B
C
D
起點 : A
todo = {C}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
拿出 B
把 B 的鄰居距離設定為自己+1
0
1
1
A
B
C
D
起點 : A
todo = {C}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
拿出 B
把 B 的鄰居距離設定為自己+1
把 B 的鄰居放入 todo
0
1
1
A
B
C
D
起點 : A
todo = {}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
拿出 B
把 B 的鄰居距離設定為自己+1
把 B 的鄰居放入 todo
拿出 C
0
1
1
A
B
C
D
起點 : A
todo = {}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
拿出 B
把 B 的鄰居距離設定為自己+1
把 B 的鄰居放入 todo
拿出 C
把 C 的鄰居距離設定為自己+1
0
1
1
2
A
B
C
D
起點 : A
todo = {D}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
拿出 B
把 B 的鄰居距離設定為自己+1
把 B 的鄰居放入 todo
拿出 C
把 C 的鄰居距離設定為自己+1
把 C 的鄰居放入 todo
0
1
1
2
A
B
C
D
起點 : A
todo = {}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
拿出 B
把 B 的鄰居距離設定為自己+1
把 B 的鄰居放入 todo
拿出 C
把 C 的鄰居距離設定為自己+1
把 C 的鄰居放入 todo
拿出 D
0
1
1
2
A
B
C
D
起點 : A
todo = {}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
拿出 B
把 B 的鄰居距離設定為自己+1
把 B 的鄰居放入 todo
拿出 C
把 C 的鄰居距離設定為自己+1
把 C 的鄰居放入 todo
拿出 D
把 D 的鄰居距離設定為自己+1
0
1
1
2
A
B
C
D
起點 : A
todo = {}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
拿出 B
把 B 的鄰居距離設定為自己+1
把 B 的鄰居放入 todo
拿出 C
把 C 的鄰居距離設定為自己+1
把 C 的鄰居放入 todo
拿出 D
把 D 的鄰居距離設定為自己+1
把 D 的鄰居放入 todo
0
1
1
2
A
B
C
D
起點 : A
todo = {}
拿出 A
把 A 的鄰居距離設定為自己+1
把 A 的鄰居放入 todo
拿出 B
把 B 的鄰居距離設定為自己+1
把 B 的鄰居放入 todo
拿出 C
把 C 的鄰居距離設定為自己+1
把 C 的鄰居放入 todo
拿出 D
把 D 的鄰居距離設定為自己+1
把 D 的鄰居放入 todo
0
1
1
2
todo 沒有資料了
搜尋完成
把每一個連通的點都標上了與起點間的距離!
// 要把 vector<> todo 改成 deque<> todo
// deque 才能操作 front
dist[s] = 0; // 起點距離為 0
while (!todo.empty()) {
v = todo.front(); // 拿前面的東西
todo.pop_front();
for (int u: V[v]) {
if (!used[u]) {
// 一發現新鄰居,放到 todo 最後面
todo.emplace_back(u);
dist[u] = v + 1; // 鄰居距離 = 自己 + 1
used[u] = true;
}
}
}廣度優先搜尋
按照與起點的距離由近到遠搜尋資料!
可以算出每一個點與起點的距離!
練習題
- ZJ d406: 倒水時間
進階練習
- e585: 12797 - Letters (Hint : 暴力枚舉字母排列)
- ZJ e699: 11624 - Fire! (Hint : 多次的 BFS)
- TIOJ 1008 . 量杯問題 (遊戲的最快獲勝法,實作較難)
有向無環圖
Directed Acyclic Graph
有向無環圖
顧名思義,一種有向圖,而且沒有環
這種圖是圖論的特例,在有向無環圖上,問題通常會比較容易解決

拓譜排序
把一個頂點當作一個工作,一份工作要開始之前,他的前置作業必須完成
是否能給出一個順序,使得每個工作開始前,他的前置作業都完成了

如果有一條路 \(a\) 到 \(b\) ,那 \(a\) 就要排在 \(b\) 前面
拓譜排序
拓譜排序的概念與前面的走訪類似

e
我們只在一個點,他的前置工作都完成時,
才把這一個點放到 todo 中
左圖中,如果要把 e 放到 todo 中
那就要先把 a,c,d 放到 todo
為什麼不用考慮 b ?
拓譜排序

e
如何算出每一個點的前置工作有幾個 ?
左圖中,如果要把 e 放到 todo 中
那就要先把 a,c,d 放到 todo
前置工作的數量,就是有幾根箭頭指向自己
就是入度 ( In degree )
| a | b | c | d | e | |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 3 | 3 |
拓譜排序

e
如何算出每一個點的前置工作有幾個 ?
前置工作的數量,就是有幾根箭頭指向自己
就是入度 ( In degree )
| a | b | c | d | e | |
|---|---|---|---|---|---|
| tasks | 0 | 1 | 1 | 3 | 3 |
如果一個點一開始就沒有前置作業 (a)
就把他丟到 todo 中!
while (M--) {
int a, b;
cin >> a >> b; // 有向邊 a->b
V[a].emplace_back(b);
tasks[b]++;
}
vector<int> todo;
for(int i=0;i<N;++i)
if (tasks[i]==0)
todo.emplace_back(i);拓譜排序

e
todo 每次拿出來的一個點
他的鄰居能直接放到 todo 嗎 ?
要檢查這個鄰居,他的前置作業都完成了,
才能放入
如何設計一個簡單快速的檢查方法呢?
每拿出一個點,就把他的鄰居 tasks - 1
表示完成了一個工作
如果鄰居變成 0 ,表示完成所有工作 !
vector<int> solution;
while (!todo.empty()) {
int v = todo.back(); // 任意拿一個出來
todo.pop_back();
solution.emplace_back(v);
for (int u:V[v])
{
tasks[u] = tasks[u] - 1;
if (tasks[u] == 0)
todo.emplace_back(u);
}
}todo 拿出來的資料,依序就是拓譜排序的結果
可以用另一個陣列存起來,或是做題目要求的事情

e
步驟1. 計算所有點的 tasks
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 1 | 1 | 3 | 3 |
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 1 | 1 | 3 | 3 |
| a |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 1 | 1 | 3 | 3 |
| a |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 1 | 1 | 3 | 3 |
| a |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 2 | 2 |
| a |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 2 | 2 |
| b | c |
|---|
| a |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 2 | 2 |
| c |
|---|
| a | b |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 2 |
| c |
|---|
| a | b |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 2 |
| c |
|---|
| a | b |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 2 |
| a | b | c |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| a | b | c |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| d |
|---|
| a | b | c |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| a | b | c | d |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| a | b | c | d |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| e |
|---|
| a | b | c | d |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| a | b | c | d | e |
|---|
Kahn's algorithm

e
步驟1. 計算所有點的 tasks
步驟2. 把 tasks 為 0 的點放入 todo
while todo 非空
從 todo 拿出一個點 p
檢查 p 的所有鄰居 v
將 v 的 tasks - 1
如果 v 的 tasks 變成 0
就把 v 放到 todo
| a | b | c | d | e |
|---|
拓譜排序的答案不為一
可能有很多種結果,都滿足拓譜排序
| a | c | b | d | e |
|---|
Kahn's algorithm

e
如果演算法結束後,如果有點沒走過
代表 圖不是有向無環圖
拓譜排序
A
B
C
D
練習題
ZJ f167: m4a1-社團 Club
#include <bits/stdc++.h>
using namespace std;
vector<int> V[1001];
int main() {
int N, M;
cin >> N >> M;
vector<int> tasks(N+1);
while (M--) {
int a, b;
cin >> a >> b; // 有向邊 a->b
V[a].emplace_back(b);
tasks[b]++;
}
vector<int> todo;
for(int i=1;i<=N;++i)
if (tasks[i]==0)
todo.emplace_back(i);
vector<int> solution;
while (!todo.empty()) {
int v = todo.back(); // 任意拿一個出來
todo.pop_back();
solution.emplace_back(v);
for (int u:V[v])
{
tasks[u] = tasks[u] - 1;
if (tasks[u] == 0)
todo.emplace_back(u);
}
}
if (solution.size() == N) {
cout << "YES\n";
for (int i:solution)
cout << i << '\n';
} else {
cout << "NO\n";
}
}
e
除此方法之外
也能用一次 DFS 找出拓譜序 (的逆序)
方法也十分簡單
拓譜排序
// 如果圖不是DAG,直接這樣用會爛掉
void dfs(int v){
used[v] = true;
for (int u:V[v])
if (!used[u])
dfs(u);
solution.emplace_back(v);
}
Q. 上面的程式碼怎麼判斷是不是 DAG ?
bool OnStack[2000];
bool used[2000];
void dfs(int v){
OnStack[v] = true;
used[v] = true;
for (int u:V[v]) {
if (!used[v]) // 沒看過
dfs(u);
else if (OnStack[u])
return ; // 不是 dag!
}
OnStack[v] = false;
solution.emplace_back(v);
}記得這個 solution 與前面演算法的剛好前後顛倒阿
進階練習
2021 全國賽 D. 汽車不再繞圈圈 (car)
ZJ a454: TOI2010 第二題:專案時程
TIOJ 1226. H遊戲
TIOJ 1092. 跳格子遊戲
2021 全國賽 D. 汽車不再繞圈圈
- 給一張有向圖,每個邊都有權重
- 請試圖反轉某些邊,使得圖沒有環
- 問要反轉的最大權重至少要是多少
跳格子遊戲 TIOJ 1092
- 有兩個人 Alice, Bob 在一張 DAG 上玩遊戲
- 一開始 Alice 站在起點,接著 Bob 選擇一個與起點相鄰的點,然後再換 Alice 選下一個相鄰點,如此交替著,直到有人到達終點為止。
- 假設一定有路到達終點,如果兩人都用最佳策略玩遊戲,請問誰必勝?
跳格子遊戲 TIOJ 1092

跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
因為沒則選擇,只能選擇移動到 "先手必敗" 的狀況 (下一回合先後手交換GG)
Note : 這一個題目是 "後手做移動",如果是 "先手做移動" 結論會有點不一'樣
跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
如果只有終點 : 先手必勝
跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
只有通向必勝的路,因此必敗
跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
終點前兩步 : 有路通向必敗,因此必勝
跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
以此推出所有點是必勝還是必敗
跳格子遊戲 TIOJ 1092

按照拓譜排序的逆序進行
單源點最短路徑
Single Source Shortest Path
單源點最短路徑
- 在前兩章,示範了 "邊最短路徑" ,解決網格圖、最少方法數的問題
- 但現實上,我們通常不會把 "邊" 都當成是一樣長的,不同的邊會有不同的邊長
- 本章要來講解 當 "邊" 不一樣長時的最短路徑解法。
A
B
C
5
10
邊權的儲存
- 在前幾章的資料結構中,都只記錄鄰居有誰
- 本章開始會有邊權,實作通常以 struct 把鄰居的編號以及邊長包裹紀錄
vector<tuple<int,int>> V; // (neighbor, length)
int s, t, w;
cin >> s >> t >> w;
V[s].emplace_back(t, w);
// V[t].emplace_back(s, w); // 雙向邊
for(auto [u, w] : V[v]) {
// do something
}從邊最短路徑 到 有權重最短路徑
- 我們已經知道了邊最短路徑是離起點近到遠的存取
- 我們假設邊長是整數,那我們可以把邊 "切割" 程單位長度
- 那麼我們就能用 "BFS" 解出有權重的最短路徑長度 !
A
B
C
3
2
A
B
C
1
1
1
1
1
從邊最短路徑 到 有權重最短路徑
- 這種 "切割" 的做法,遇到很長的邊效率很糟糕
- 而且我們根本不在意中間經過的點 !
- 因此,我們要怎麼樣很快地知道 BFS 下一個會遇到的頂點是哪一個 ?
A
C
1
1
1
1
1
2
B
1
1
1
1
1
1
頂點 A :
現在 B 距離我 9
現在 C 距離我 2
從邊最短路徑 到 有權重最短路徑
- 從已遍歷的點中,找 從 "起點" 到 "自己" 再到 "鄰居"的方法中,答案最小的,就是下一個 BFS遇到的點 !
A
C
1
1
1
1
1
2
B
1
1
1
1
1
1
頂點 A :
現在 B 距離我 9
現在 C 距離我 2
<= 下一個遇到的是 C
從一群東西找最小 : Priority Queue !
實作要點
- 使用一個陣列紀錄答案是否被求出
- 另外使用一個陣列紀錄答案。預設初始化為 無限大
- 由於計算過程中可能會把兩個無限大相加,無限大要比最大值一半還要小
- 按實作方法、演算法而定,但建議都要這樣做
int Dijkstra(int s, int e, int N) {
const int INF = INT_MAX / 2;
vector<int> dist(N, INF);
vector<bool> used(N, false);
dist[s] = 0;
}實作要點
- 另一種使用 memset 設定無限大的做法
-
0x3f3f 大概比最大正整數 0x7fff 一半 0x3fff 小一點
int dist[2000];
int Dijkstra(int s, int e, int N) {
memset(dist, 0x3f, sizeof(dist));
const int INF = dist[0];//0x3f3f3f3f
dist[s] = 0;
}也可以用 for loop / fill / fill_n 之類的來設定陣列數值
Priority_Queue 拿最小
- C++ 預設的 priority queue 拿的是最大值,若要最大需要改寫 !
方法 1. 改符號方向
C++ 預設用 小於 (less) 比較,我們換成 大於(greater)
using T = tuple<int,int>;
priority_queue<T, vector<T>, greater<T>> pq;Priority_Queue 拿最小
- C++ 預設的 priority queue 拿的是最大值,若要最大需要改寫 !
方法 2. 自訂比較函數 (函數物件)
struct cmp {
bool operator()(int a, int b) {
return a > b;
}
};
priority_queue<T, vector<T>, cmp> pq;Priority_Queue 拿最小
- C++ 預設的 priority queue 拿的是最大值,若要最大需要改寫 !
方法 3. 自訂比較函數 (一般函數)
個人較不建議這樣寫
bool cmp(int a, int b) {
return a > b;
}
priority_queue<T, vector<T>, decltype(&cmp)> pq(cmp);
// priority_queue<T, vector<T>, function<bool(int, int)>> pq(cmp);
int Dijkstra(int s, int e, int N) {
const int INF = INT_MAX / 2;
std::vector<int> dist(N, INF);
using T = tuple<int,int>;
priority_queue<T, vector<T>, greater<T>> pq;
dist[s] = 0;
pq.emplace(0, s); // (w, e) 讓 pq 優先用 w 來比較
}實作細節
- 其餘部分與 BFS 差不多,我們對於更好的答案,直接放到 priority queue 裡面
- 因此一個點可能會出現很多次,我們只關心每一個點 "第一次" 出現的時候。
while (!pq.empty()) {
tie(std::ignore, s) = pq.top();
pq.pop();
if ( used[s] ) continue;
used[s] = true; // 每一個點都只看一次
for (auto [e, w] : V[s]) {
if (dist[e] > dist[s] + w) {
dist[e] = dist[s] + w;
pq.emplace(dist[e], e);
}
}
}存在更好的實作,可以更新 heap 裡的資料,而不是塞垃圾到 heap 裡面,然後再篩選資料
int Dijkstra(int s, int e, int N) {
const int INF = INT_MAX / 2;
vector<int> dist(N, INF);
vector<bool> used(N, false);
using T = tuple<int,int>;
priority_queue<T, vector<T>, greater<T>> pq;
dist[s] = 0;
pq.emplace(0, s); // (w, e) 讓 pq 優先用 w 來比較
while (!pq.empty()) {
tie(std::ignore, s) = pq.top();
pq.pop();
if ( used[s] ) continue;
used[s] = true; // 每一個點都只看一次
for (auto [e, w] : V[s]) {
if (dist[e] > dist[s] + w) {
dist[e] = dist[s] + w;
pq.emplace(dist[e], e);
}
}
}
return dist[e];
}Dijkstra 演算法
- 經典的圖論演算法,該演算法假設所有的邊都大於等於 0 ,以便把模型轉程 BFS 來解決
- 由於前述限制,如果邊長有負數,此方法無法得出正確答案
A
B
C
2
3
-6
A 到 B 的最短路徑是 A->C->B ,答案為 -3 ,但是 dijkstra 會把最先出現的 A->B = 2 當作答案。
時間複雜度
- Dijkstra 的複雜度與找最大值的方法有關
大致等於:
找最大值的複雜度 x 次數 + 把資料放入資料結構複雜度 x 次數
- 範例實作使用內建的 priority queue
- 每一條邊都可能進入 pq ,複雜度為 \(O(E\log E)\)
- 每一條邊都可能進入 pq ,複雜度為 \(O(E\log E)\)
- 實作可更新資料的 priority queue
- 最多只有 \(V\) 個點在 pq ,複雜度為 \(O(E\log V)\)
- 最多只有 \(V\) 個點在 pq ,複雜度為 \(O(E\log V)\)
- 最低可到 \(O(E+V\log V)\) 比賽用不到,常數過大
- fibonacci heap : 更新平攤 \(O(1)\)
| 找最大值 | 次數 | 更新資料 | 次數 | 總複雜度 | |
|---|---|---|---|---|---|
| 內建的 priority queue | 1 | E | log E | E | E log E |
| 用陣列暴力做 | V | V | 1 | E | V^2+E |
| 實作可更新資料的 priority queue | 1 | E | log V | E | E log V |
| Fibonacci Heap | log V | V | 1 | E | E+Vlog V |
練習題
- uva 10986 Sending email
負邊處理
- 由於 dijkstra 的模型缺陷,我們無法用它來處理有負邊的邊長
- 因此我們要來介紹另一個能夠處理負邊的演算法
負環偵測
- 如果一個圖存在一個環,其路徑總和為負數,便會讓部分答案變成無限小
- 目前已知 在有負環的圖 找最短路徑,是 NP-Hard 的問題,一般演算法無法正常處理,因此要在發生負環錯誤時,要能偵測出該錯誤
A
B
C
-5
-3
-6
D
8
Relax
- 定義 \(d(x)\) 表示當前已知由起點到 \(x\) 的最短路徑
對於每一條邊 \(s\stackrel{w}\to e\) ,如果有
$$d(e) > d(s) + w$$
那我們就需要 relax
也就是把 \(d(e)\) 更新成更好的答案 \(d(s)+w\)
Bellman Ford Algorithm
- 如果不存在任意一條邊要 relax ,那 \(d(x)\) 收斂於最短路徑
- 對每條邊拼命 relax 到不能為止 !
- 對每條邊拼命 relax 到不能為止 !
- 對於要 "看過每一條邊" 的演算法,使用 "邊陣列" 來儲存比較方便
vector<tuple<int,int,int>> Edges; // (s, t, w)Bellman Ford
- 非常簡單暴力的演算法
vector<tuple<int,int,int>> Edges;
int BellmanFord(int s, int e, int N) {
const int INF = INT_MAX / 2;
vector<int> dist(N, INF);
dist[s] = 0;
bool update;
while (true) {
update = false;
for(auto [v, u, w] : Edges)
{
if (dist[u] > dist[v] + w)
{
dist[u] = dist[v] + w;
update = true;
}
}
if (!update)
break;
}
return dist[e];
}
時間複雜度
- 執行 \(n\) 次的 Bellman Ford 可以求出經過邊數小於等於 \(n\) 的最短路徑
- 如果圖沒有負環,最短路徑最多只會用 \(V-1\) 條邊,因此複雜度為 \(O(VE)\)
- 如果迴圈執行到第 \(V\) 次仍有 update ,表示有使用超過 \(V-1\) 條邊的最短路,也就是有負環,可以用此來判斷 !
- 如果不判斷會進入無窮迴圈 ! 除非題目保證沒有負環,不然要記得判斷
- 如果迴圈執行到第 \(V\) 次仍有 update ,表示有使用超過 \(V-1\) 條邊的最短路,也就是有負環,可以用此來判斷 !
vector<tuple<int,int,int>> Edges;
int BellmanFord(int s, int e, int N) {
const int INF = INT_MAX / 2;
vector<int> dist(N, INF);
dist[s] = 0;
bool update;
for(int i=1;i<=N;++i) {
update = false;
for(auto [v, u, w] : Edges)
{
if (dist[u] > dist[v] + w)
{
dist[u] = dist[v] + w;
update = true;
}
}
if (!update)
break;
if (i == N) // && update
return -1; // gg !
}
return dist[e];
}練習題
- uva 558 (負環!)
All pair shortest path
- Bellman Ford 的概念可以加以延伸,用來快速求任兩點間的最短路
- 設 \(d(a,b)\) 表示 \(a\) 到 \(b\) 已知的最短距離
對於任三點 \(a, b, c\) ,如果有
$$d(a, c) > d(a,b) + d(b,c)$$
那我們就需要 relax
也就是把 \(d(a,c)\) 更新程更好的答案 \(d(a,b)+d(b,c)\)
Floyd warshall
- 使用鄰接矩陣儲存任兩點間距離,然後瘋狂 relax
- 一開始 \(d[i][j]\) 表示 \(i\) 到 \(j\) 最短的邊長距離
- 小心重複的邊 !
- \(i\) 到 \(j\) 沒有邊的話設無限大
- 自己到自己 \(d[i][i] = 0\)
- 一開始 \(d[i][j]\) 表示 \(i\) 到 \(j\) 最短的邊長距離
int d[MAXN][MAXN];Floyd warshall
- 實作極簡單 \(O(V^3)\)
- 裡面兩個迴圈 \(i,j\) 是枚舉所有邊
- 最外面 \(k\) 是枚舉中間點
int d[100][100];
void FloydWarshall(int N){
for(int k=0;k<N;++k)
for(int i=0;i<N;++i)
for(int j=0;j<N;++j)
if(d[i][j] > d[i][k] + d[k][j])
d[i][j] = d[i][k] + d[k][j];
}練習題
UVa 11463
整理
| 功能 | 複雜度 | 缺點 | |
|---|---|---|---|
| Dijkstra | 求單一起點最短路 | O(E log E) | 不能有負邊 |
| BellmanFord | 求單一起點最短路 負邊處理 |
O(EV) | 複雜度高 |
| SPFA | 求單一起點最短路 負邊處理 |
O(Ek) | 比賽容易被卡,會跟 Bellman Ford 一樣爛 |
| FloydWarshall | 任兩點最短路 | O(V^3) | 專解任兩點最短路 |
0
3
1
2
4
5
6
7
8
4
4
2
4
9
4
3
8
1
3
3
10
1
最小生成樹
Mininum Spanning Tree
Tree
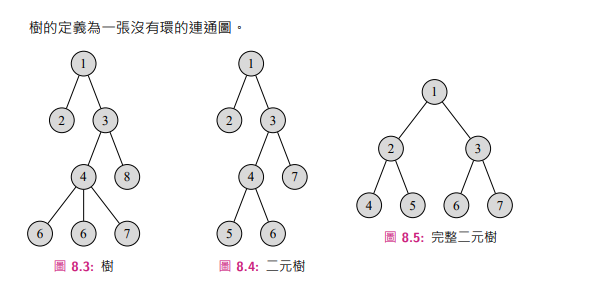
Tree
= 由 \(n\) 個點 \(n-1\) 條邊構成的聯通圖
= 在任兩點加上邊就會有環的無環圖
生成樹
- 一個圖的生成樹,是圖的子集,為包含所有頂點的樹
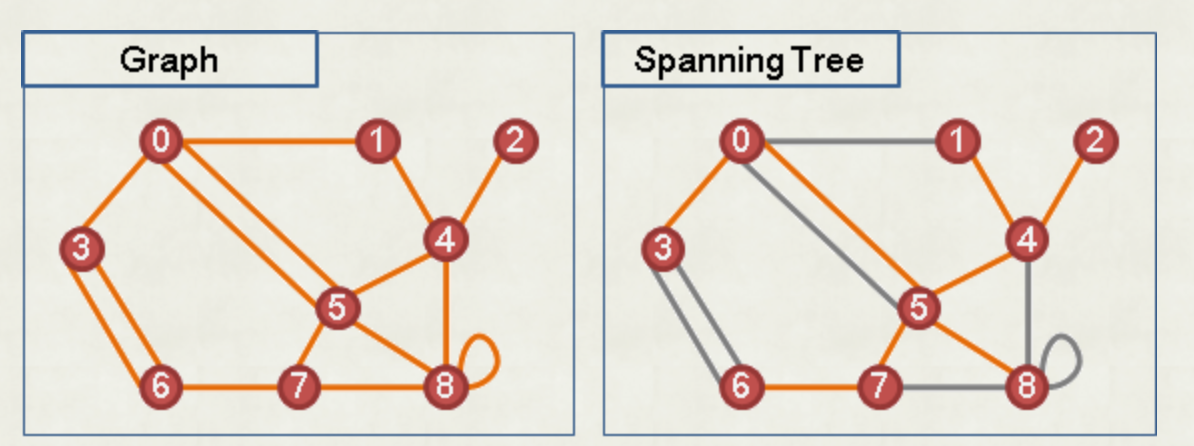
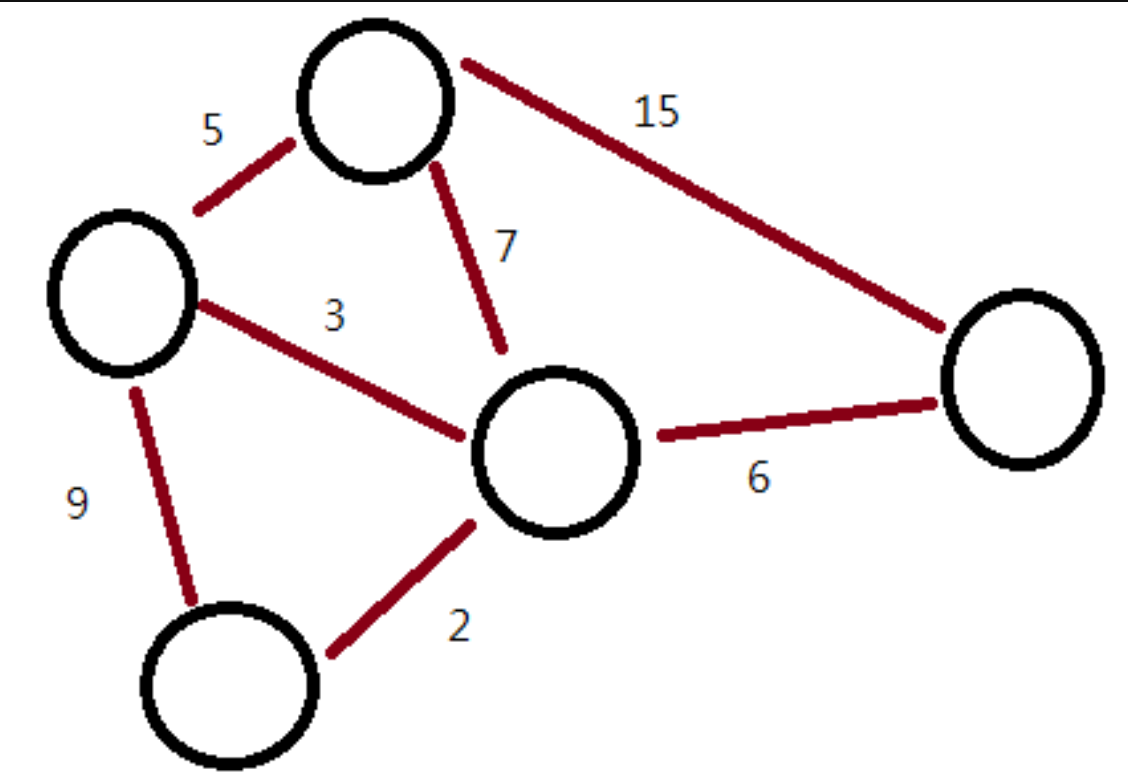
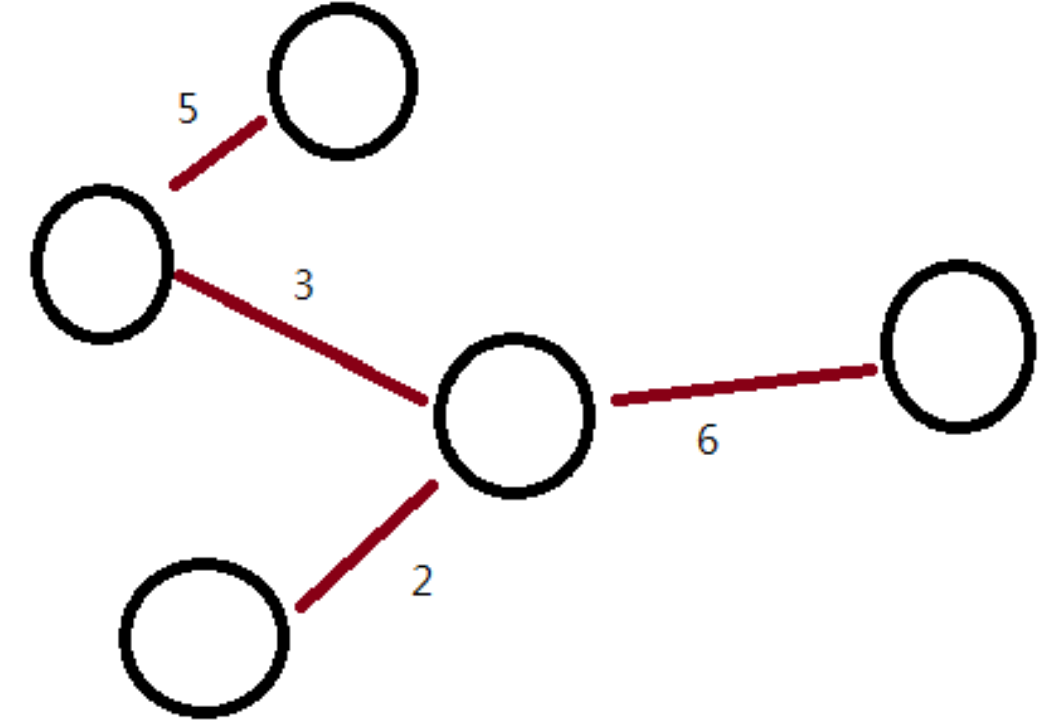
最小生成樹
- 最小生成樹為一張圖的生成樹中,邊權總和最小的樹
最小生成樹
- 最小生成樹為一張圖的生成樹中,邊權總和最小的樹
Kruskal's algorithm
- 競賽中,常使用 kruskal 演算法來求最小生成樹
- 該演算法需要使用 disjoint set @
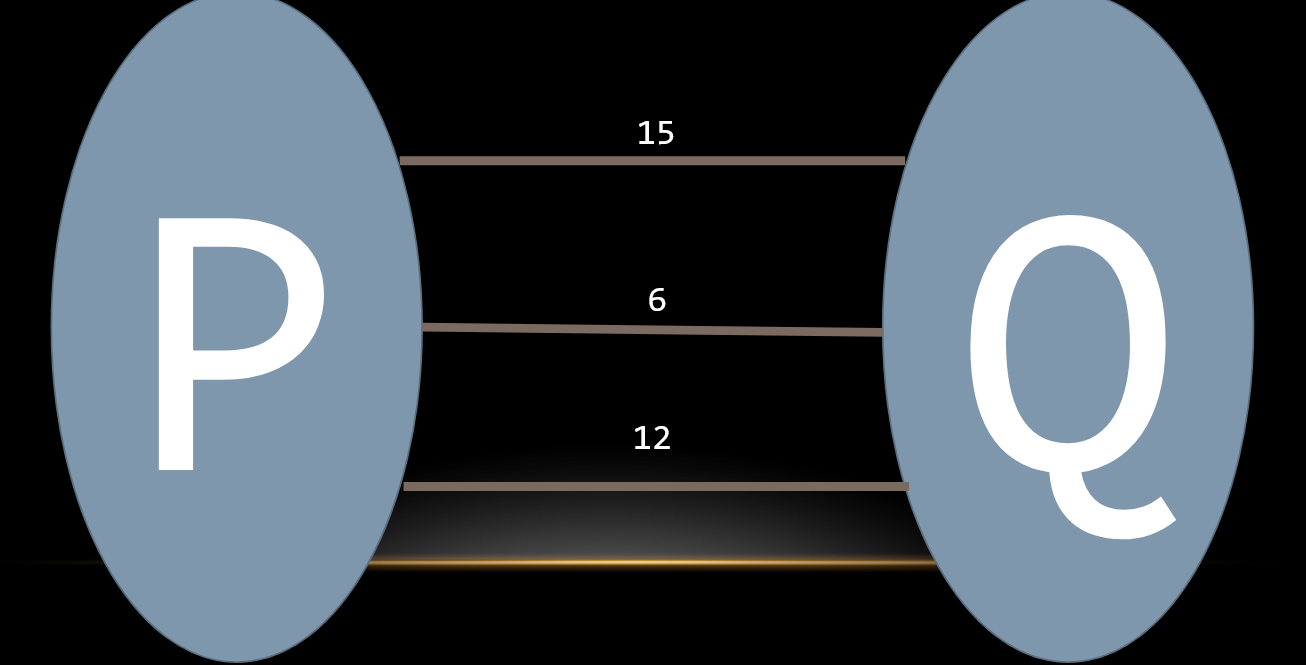
最小生成樹定理
- \(P,Q\) 分別為最小生成樹的集合,欲使用一些邊將 \(P,Q\) 合併
- 使用最小權重的邊將 \(P\)、\(Q\) 連接,合併後的樹依然是最小生成樹
Kruskal 's algorithm
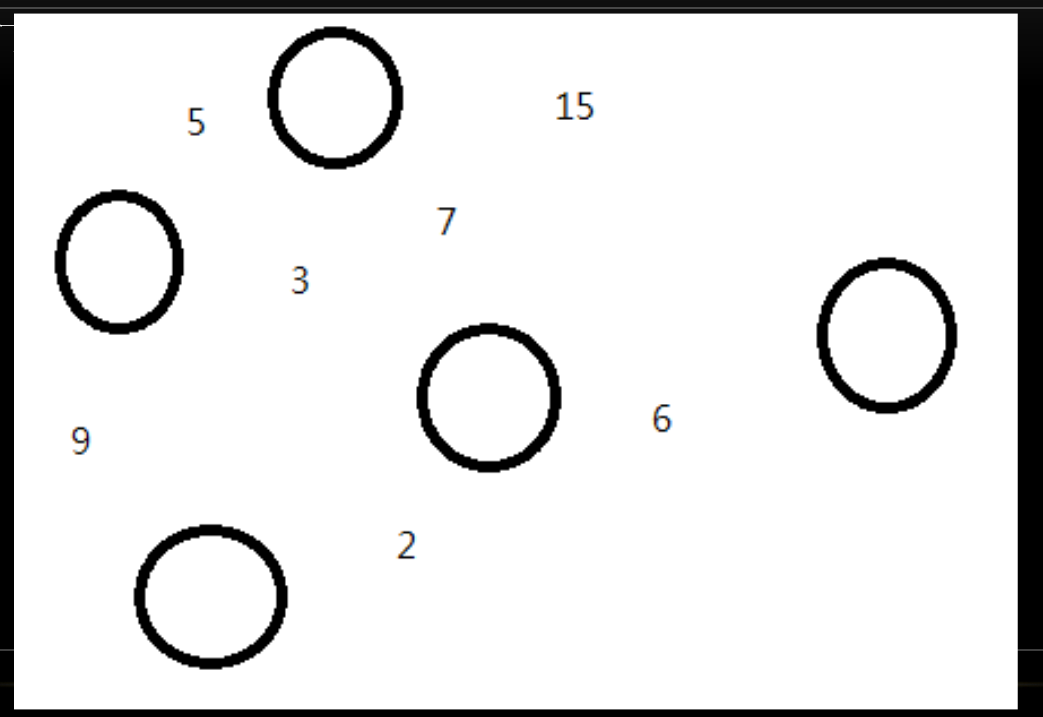
- 透過前定理,我們可以使用貪心法來作出最小生成樹
- 先將所有邊由小到大排序
- 依序考慮每條邊,如果這條邊的兩端沒有在同一個子樹上就加入這條邊
- 完成!
vector<tuple<int,int,int>> Edges;
int kruskal(int N) {
int cost = 0;
sort(Edges.begin(), Edges.end());
DisjointSet ds(N);
sort(Edges.begin(), Edges.end());
for(auto [w, s, t] : Edges) {
if (!ds.same(s, t)) {
cost += w;
ds.unit(s, t);
}
}
return cost;
}
時間複雜度 : \(O(E\log E)\)
練習題
uva 10034-Freckles
ZJ e509: Conscription
uva 10048 - Audiophobia
uva 534 - Frogger
兩點間最小瓶頸
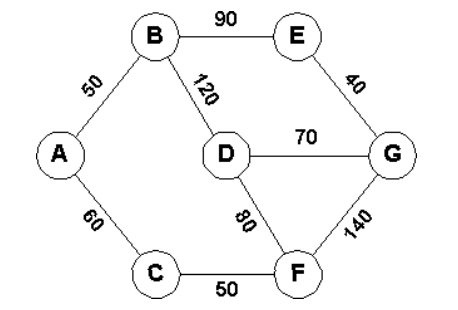
基本解法 : 二分搜、或構造成 MST,最短路問題