Graph\(^+\)
By LFsWang
DFS Tree
DFS Tree
- 由一個點做 DFS 之後構成的樹
- 根據邊的在遍歷的過程中連接狀態有不同性質
DFS Tree

DFS Tree
定義 \(P(v)\) 表示點 \(v\) 在 DFS Tree 的父節點
而 \(P(\text{root})\) 是空節點
DFS Tree
Tree edge : DFS 過程中行走的邊
(下一個點是沒走過的)
void dfs(int v, int fa) {
used[v] = true;
for (auto u:V[v]) {
if (!used[u]) {
dfs(u, v); // tree edge (v->u)
}
}
}DFS Tree
Back edge : 接觸到目前祖先的邊
(因此這條邊與 Tree edge 會形成環)
Root
DFS Tree
如果 \(G\) 是 連通無向圖,則
\(G\) 的 DFS Tree 只由下兩種邊構成
- Tree edge
- Back edge
Root
DFS Tree
\(p\)
Proof.
\(v\) 是 \(p\) 的子節點
設 \(p\) 有一條邊走到了 \(a\),而 \(a\) 已被標記已走過,而且 \(a\) 不是 \(v\) 的祖先
根據 DFS 的演算法,表示 \(a\) 為根的子樹已經被遍歷
考慮點 \(v\)
因為有路徑 \(a\to v\),故 \(v\) 也被遍歷了
故 \(v\) 不再參與走訪
因此透過 \(v\) 走訪 \(a\) ,與目前狀態矛盾
\(a\)
\(v\)
DFS Tree
Root
Forward edge : 會到目前點先繼點的邊
(這條邊會到目前點的更深處)
Forward edge
DFS Tree
Root
Cross edge : 會到目前點無相關子樹的邊
(這條邊必不與 Tree edge 產生迴圈)
Cross edge
DFS Tree
- 圖論題目絕大多數演算法都跟 DFS / BFS 有關
- 而 DFS Tree 是一種有條理整理 case 的方法
- 將行走的邊分類,思考對應的決策
| 無向圖 | 有向圖 |
|---|---|
| Tree edge | Tree edge |
| Back edge | Back edge |
| Cross edge | |
| Forward edge |
Forward edge (實作限制)
Connected Component
連通分量
設集合 \(C\) 為無向圖 \(G\) 的一個連通分量
若點 \(x,y\in G\)
\(x,y \in C\Leftrightarrow x,y\) 之間有一條路徑
連通分量
連通分量
鄰點:若存在邊 \(e(v,w)\),則 \(v\), \(w\) 互為鄰點
因此 \(v\) 的鄰居 \(N(v)\) 是 \(v\) 的邊可以到達的所有點集合。
路徑:若 \(a,b\) 在同一個連通塊
\(\operatorname{path}(a,b)\) 表示 a 到 b 的任意一種路徑。
連通分量
- 每一個點都位在一個連通分量
- 若有路徑 \(\operatorname{path}(x,y)\),就有 \(\operatorname{path}(y,x)\)
- 若存在 \(\operatorname{path}(x,y),\operatorname{path}(y,z)\),就存在 \(\operatorname{path}(x,z)\)
看起來就像disjoint set
連通分量
連通分量測試
定義函數 \(C(g)\) 表示圖 \(g\) 的連通分量數量,給定一張無向圖 \(G\)
- 求\(C(G)=?\)
DFS
根據連通分量的特性,DFS 任意一個點會走遍該點的連通分量
因此就看用了幾次 DFS 就能知道答案
AP & Bridge
關節點與橋
Articulation Points
有一張無向連通圖\(G\)
若點 \(v\) 是關節點 (AP) \(\Leftrightarrow\) \(G\) 刪除 \(v\) 後,\(C(G)>1\)
Bridge
有一張無向連通圖
若邊 \(e\) 是橋 \(\Leftrightarrow\) 從 \(G\) 刪除 \(e\) 後,\(C(G)>1\)
關節點與橋
給一張無向圖,請找出圖裡面所有的關節點 (與橋)。
DFS 爆搜
枚舉所有的點當關節點,模擬刪掉後,是否依然能遍歷所有的節點
橋亦同
DFS:\(O(E+V)\)
總複雜度:\(O((E+V)^2)\)
Tarjan's algo for AP
圖論大師 Tarjan 在1973年提出了在 \(O(n)\) 時間找出AP的演算法
實際上同方法也可以用來找 Bridge
note. \(O(n)\) 在圖論表示 \(O(E+V)\)
定義 \(T\) 是 \(G\) 的 DFS Tree
對於點 \(v \in G\),定義函數如下
Depth \(D(v)\):表示點 \(v\) 在 \(T\) 的深度
$$D=1$$
$$D=2$$
$$D=3$$
$$D=4$$
定義 \(T\) 是 \(G\) 的 DFS 搜索樹
對於點 \(v \in G\),定義函數如下
Lowpoint \(L(v)\) :
在不通過往 parent 的 tree edge 路徑上,
自己、
所有能透過 tree edge 走到的點,
以及前述所有點透過 back edge 連接的點中,
\(D(x)\) 的最小值
parent
X
Quick Hint : 只有 "自己"、或 "Back edge" 連接點會是 L(x) 的答案
Low point
✔
✔
✔
自己
子樹
子樹的臨點
(紅色勾勾的鄰居)
\(L(x)\) 是打勾部分 \(D(x)\) 的最小值
✔
臨點
X
\(D(x)\) 小 <--------------------------------> 大
Low point
可以利用子樹的答案來推出自己的 Lowpoint
a 是 v 的臨點,不包含 parent
b 是 v 子樹的根結點
$$L(v) = \min( D(v),D(a),L(b) )$$
Tarjan's algo for AP
定理1. 根節點 \(r\) 是 AP \(\Leftrightarrow \deg(r) > 1\)
Proof
若移除 \(r\) 會使原圖產生 \(\deg(r)\) 個連通分量
根據AP的定義得證
DFS tree 中 根root 通常是特例 !!
Tarjan's algo for AP
定理2. \(v\) 是非 root 的點,w 是 \(v\) 的鄰點。
若 \(v\) 是 AP \(\Leftrightarrow \exists w :L(w)\geq D(v)\)
\(v\)
\(w\)
\(L(w)\)
因為 w 無法走到比v 還要前面的點
移除 v 必然會至少分成 w 與 r 的兩個連通分量
\(r\)
Tarjan's algo for Bridge
定理3. \(v\) 是非 root 的點,\(w\) 是 \(v\) 的鄰點。
若 \(e(v,w)\) 是 Bridge \(\Leftrightarrow \exists w :L(w) > D(v)\)
\(v\)
\(w\)
\(L(w)\)
因為 w 無法走到比w 還要前面的點
移除 e 必然會至少分成 w 與 r 的兩個連通分量
\(r\)
\(e(v,w)\)
Tarjan's algo for AP
在 Tarjan 的原始論文中,D(x) 是定義為 DFS 遍歷順序的時間戳,也是較為常見的實作方法
實際上只需要保證 DFS 時每一條向下的通路 D(x) 遞增就行
Tarjan's algo for AP
void DFS(int v, int fa) //call DFS(v,v) at first
{
D[v] = L[v] = timestamp++; //timestamp > 0
int childCount = 0; //定理1 for root
bool isAP = false;
for (int w:adj[v])
{
if( w==fa ) continue;
if ( !D[w] ) // D[w] = 0 if not visited
{
DFS(w,v);
childCount++;
if (D[v]<=L[w]) isAP = true; //定理2
if (D[v]< L[w]) edgeBridge.emplace_back(v, w);//定理3
L[v] = min(L[v], L[w]);
}
L[v] = min(L[v], D[w]);
}
if ( v == fa && childCount < 2 ) isAP = false; //定理1, v==fa只是確認root
if ( isAP ) nodeAP.push_back(v);
return ;
}練習題
給圖找Cutting Point
UVa 315
有重邊版本 (注意Lowpoint定義)
hdu4612
Bridge &
Bridge-connected Component
橋與橋連通分量
橋連通分量
- 如果把一張圖所有的橋去除,我們稱這樣的區塊分割方法為橋連通分量
橋
橋連通分量
橋連通分量
橋連通分量
橋
橋連通分量
橋
橋連通分量的縮點
如果將一張圖同一個 BCC 所有點合併成一個點,會構成一棵樹
(顯然的,這樹上的每一條邊都是橋)
可以利用此性質將圖的問題轉換為樹的問題加以思考!

橋連通分量
- 要如何求橋連通分量 ?
- 方法1. 先求出橋,把橋砍掉,剩下的點再慢慢編號
- 方法2. 在 Tarjan 中順便做
橋連通分量
- hint : 如果發現 \(L[v] = D[v]\) ,表示發現了一個橋的端點
- 那顯然的這裡應該是橋連通分量的分界,這一個點只會與他的子樹形成橋連通分量
橋
\(L[v]=D[v]\)
橋連通分量
- 利用前序走訪把點放入 Stack ,就能知道自己的子樹有什麼點
void dfs (int v, int fa) {
st.push(v);
/* 繼續 dfs v 的子樹 */
if (想看子樹有誰) {
int x;
do {
x = st.pop(); // 彈出子樹節點
} while (x!=v);
}
}橋連通分量
- 如果發現了一座橋,就把這個橋連接到的所有點砍掉
- 被砍掉的點會在同一個橋連通分量
橋
\(D[v]=L[v]\)
橋連通分量
- 如果發現了一座橋,就把這個橋連接到的所有點砍掉
- 被砍掉的點會在同一個橋連通分量
砍掉
stack 彈出來
橋連通分量
- 如果發現了一座橋,就把這個橋連接到的所有點砍掉
- 被砍掉的點會在同一個橋連通分量
橋
\(D[v]=L[v]\)
橋連通分量
- 如果發現了一座橋,就把這個橋連接到的所有點砍掉
- 被砍掉的點會在同一個橋連通分量
砍掉
stack 彈出來
橋連通分量
- 如果發現了一座橋,就把這個橋連接到的所有點砍掉
- 被砍掉的點會在同一個橋連通分量
橋
\(D[v]=L[v]\)
橋連通分量
- 如果發現了一座橋,就把這個橋連接到的所有點砍掉
- 被砍掉的點會在同一個橋連通分量
砍掉
stack 彈出來
橋連通分量
void DFS(int v, int fa) { //call DFS(v,v) at first
D[v] = L[v] = timestamp++; //timestamp > 0
st.emplace(v);
for (int w:adj[v]) {
if( w==fa ) continue;
if ( !D[w] ) { // D[w] = 0 if not visited
DFS(w,v);
L[v] = min(L[v], L[w]);
}
L[v] = min(L[v], D[w]);
}
if (L[v]==D[v]) {
bccid++;
int x;
do {
x = st.top(); st.pop();
bcc[x] = bccid;
} while (x!=v);
}
return ;
}剩下的部分與橋相同
橋連通分量
練習題
POJ 3177 = POJ 3352
給一個連通無向圖,問至少加入幾條邊使得無向圖中沒有橋
(點)雙連通分量
Biconnected Component (BCC)
BCC
- 如果一個連通分量沒有割點 (表示也沒有橋)
- 則該分量為雙連通分量

BCC
- 一個圖的雙連通分量分塊是將圖中同一個雙連通分量的點標記起來
- 與橋連通分量相似的地方是,雙連通分量以割點為分界
- 不一樣的地方是,相鄰的雙連通分量共用頂點 (割點)
割點
割點
橋
割點
BCC
- 要如何求雙連通分量 ?
- 方法1. 先求出割點,把割點標記,從割點邊界 dfs 找出來
- 方法2. 在 Tarjan 中順便做
割點
割點
橋
割點
BCC
- 方法與邊連通分量很像,但是收縮時不是把整個子樹砍掉,要留下自己 (割點)!
- 很明顯的,這方法最後會留下一個 root (多測資輸入小心)
割點
\(L[u]\geq D[v]\)
割點
BCC
stack<tuple<int,int>> st; // 以紀錄邊為主的堆疊 !!
void DFS(int v, int fa) { // call DFS(v,v) at first
D[v] = L[v] = timestamp++; //timestamp > 0
for (int w:adj[v]) {
if( w==fa ) continue;
if ( !D[w] ) { // D[w] = 0 if not visited
st.emplace(v, w); // 堆疊上壓入的是邊 !
DFS(w,v);
L[v] = min(L[v], L[w]);
if (L[w] >= D[v]) { // 找到割點!
// 收縮
}
}
L[v] = min(L[v], D[w]);
}
return ;
} // 用完我 stack 要記得清乾淨!!
stack<tuple<int,int>> st;
void DFS(int v, int fa) { //call DFS(v,v) at first
D[v] = L[v] = timestamp++; //timestamp > 0
for (int w:adj[v]) {
if( w==fa ) continue;
if ( !D[w] ) { // D[w] = 0 if not visited
st.emplace(v, w);
DFS(w,v);
L[v] = min(L[v], L[w]);
if (L[w] >= D[v]) { // 找到割點!
int x, y;
bcc.push_back({});
do {
tie(x, y) = st.top(); st.pop();
bcc.back().emplace_back(y);
} while (tie(x, y) != tie(v, w));
bcc.back().emplace_back(v);
}
}
L[v] = min(L[v], D[w]);
}
return ;
} // 用完我 stack 要記得清乾淨!!BCC 的縮點
- 雙連通分量同樣也可以縮點變成一個 Tree
- 縮點時,把圖轉成 BCC 與割點的連接關係,產生的 Tree 稱之為 Block-cut tree
割點
割點
橋
割點
BCC 的縮點
- 雙連通分量同樣也可以縮點變成一個 Tree
- 縮點時,把圖轉成 BCC 與割點的連接關係,產生的 Tree 稱之為 Block-cut tree
割點
割點
割點
Block Cut Tree 是區塊-割點交錯組成的
BCC
練習題
HDU 3749 Financial Crisis
- 問任兩個點之間有幾條互斥通路 (0/1/2+)
BCC
補充 雙連通分量的一些性質
1. 雙連通分量如果是 2 - connnect 的,至少要三個點
特例!
BCC
補充 雙連通分量的一些性質
2. 雙連通分量如果是 2 - connnect 的
表示任兩點間存在兩條互斥路徑 (環)
且
任兩邊可以找到一個環,包含該兩邊
BCC
補充 雙連通分量的一些性質
3. 雙連通分量如果是 2 - connnect 的
如果該連通分量有一個奇環
雙連通分量的任一點都被至少一個奇環覆蓋
Strongly Connected Component
強連通分量
SCC定義
令 G 是有向圖,\(v,w\) 是 G 上的兩點,\(S\) 是 G 的一個 SCC,
$$v,w \in S \Leftrightarrow \exists \operatorname{path}(v,w),\operatorname{path}(w,v)$$
SCC 由數個有向環構成!
SCC與縮點
縮點操作
將同一個強連通分量內的所有節點合併為一個點,構成一張新圖。

SCC與縮點
定理4.設 \(G'\) 是 \(G\) 經由縮點操作生成的圖
\(G'\) 是有向無環圖 (DAG)
SCC與縮點
Proof.
若 \(G'\) 有環,那這一個環構成一個 SCC,根據縮點操作,這個環必須合併成一個點,故 \(G'\) 不存在環
SCC
有兩個線性方法可以求 SCC
- Tarjan's SCC Algorithm
- Kosaraju's Algorithm
Tarjan's SCC Algorithm
圖論大師 Tarjan 在連通分量有許多著作,這也是其中一個
方法沿用了前一個演算法的 \(L(x),D(x)\) 函數
Tarjan's SCC Algorithm
定理5. 若點 \(v\) 有 \(L(v)=D(v)\),\(v\) 子樹所有未縮點的點構成 SCC
Tarjan's SCC Algorithm
定理5. 若點 \(v\) 有 \(L(v)=D(v)\),\(v\) 子樹所有未縮點的點構成 SCC
小心再有向圖上算 Low point 時,會有 Cross edge !
Tarjan's SCC Algorithm
void DFS(int v, int fa) { //call DFS(v,v) at first
D[v] = L[v] = timestamp++; //timestamp > 0
st.push(v);
inSt[v] = true;
for (int w:adj[v]) {
if ( !D[w] ) { // D[w] = 0 if not visited
DFS(w,v);
L[v] = min(L[v], L[w]);
} else if (inSt[w]) { // it is different!
L[v] = min(L[v], D[w]);
}
}
if( D[v] == L[v] ) {
int x;
do {
x = st.top();
st.pop();
scc[x] = SCCID;
inSt[x] = false;
} while( x != v );
SCCID++;
}
}Kosaraju's Algorithm
兩次 DFS 的方法
用後序走訪走過整張圖放入 stack
由 stack 一個一個拿出來在反圖 DFS,走到的都是該點的 SCC
Kosaraju's Algorithm
void DFS(vector<int> *dG, int v, int k=-1){
visited[v] = true;
scc[v] = k;
for (int w:dG[v])
if (!visited[w])
DFS(dG,w,k);
if(dG==G) st.push(v);
}
int Kosaraju(int N){
memset(visited,0,sizeof(visited));
for(int i=0; i<N; ++i) if(!visited[i]) DFS(G,i);
memset(visited,0,sizeof(visited));
while(!st.empty()){
if (!visited[st.top()]) DFS(GT, st.top(), sccID++);
st.pop();
}
return sccID;
}練習題
給定一些骨牌,且已知推倒每張骨牌會連動哪一些骨牌,問至少需推倒幾張骨牌才能使所有骨牌都倒下。
UVa 11504
https://codeforces.com/contest/1547/problem/G
CF #731 (Div. 3) G. How Many Paths?
CF #545 (Div. 1) C. Museums Tour
2-SAT
滿足性問題
SAT問題
以 AND 運算將許多 OR 運算式合併成的算式
$$(a \lor b \lor c )\land (c \lor \neg b \lor d )\land (e)=1?$$
如果在最多 OR 的子運算式中,最多只有 \(K\) 個變數,
那麼我們稱這一個問題為 K-SAT 問題。
SAT問題
定理 7. 所有 SAT 問題都能轉換成 3-SAT 問題
定理 6. 所有 NPC 問題都能轉換成 SAT 問題
定理 8. 3-SAT 問題是 NPC 問題
2-SAT
如果 3-SAT 問題可以被進一步化簡為 2-SAT 問題
定理 9. 2-SAT 問題是 P 問題
Krom's Algorithm
可以在 \(O(n)\) 的時間判定 2-SAT 問題
$$(a \lor b)\land (c \lor \neg b )\land (e)=1?$$
運用 SSC 的概念
依賴關係
考慮布林式 \(a \lor b\),若要讓此式子為 true
若 a 選擇 false,b 一定要選 true
若 b 選擇 false,a 一定要選 true
依賴關係
將 2SAT 依賴關係表示成一張圖 \(G_r\)
有向邊 (A,B) 表示若選擇 A,就要選擇 B
$$B'$$
$$A'$$
$$A$$
$$B$$
\(X'\)表示X使用false的狀態
依賴關係
怎麼連 ?
( not a or b )
( a )
( not a )
( a xor b )
Krom's Algorithm
定理10. 若 2-SAT 問題無解,則存在 X 使
\(X,X'\)位在同一個 SCC
反之,可以構造一組可行的解
( 對於每一個變數選擇拓譜排序後順位較後者 )
X = true
X = false
練習題
hdu 3062
Tree
樹
定根
- 除了資料結構的二元樹之外,更多的狀況下會以圖的方式表示樹。
- 沒有根的樹不好討論,選一個點當作 \(\text{root}\) 來轉成有根樹。
- 除了用 0 或 1 來當作根之外,還有沒有一些特別的點 ?
- 一個樹,至少存在一個重心 \(c\)
- 重心的 最大子樹大小 是最小的
- 所有子樹大小 \(\leq n/2\)
樹重心
最多可能有兩個重心

樹重心的特點
- 樹重心到所有點距離總和最短 (歸納法證明)
- 最大最大子樹大小 \(\leq n/2\)
- 每次遞迴資料量減半
- 因此遞迴處理資料只要 \(O(\log n)\) 層就會結束
- 這個性質保證利用這個點分割複雜度通常不錯,因此有了樹分治的解題策略
- 若合併資料的複雜度不超過 \(O(n)\),總複雜度通常為 \(O(n\log n)\)
- 若合併資料的複雜度不超過 \(O(n\log n)\),總複雜度通常為 \(O(n\log^2 n)\)
int sz[100001];
int center, csize; // csize = INT_MAX; for init
int _N; // ensure _N is how many node of the tree
void dfs(int v, int fa) {
int maxsub = 0;
sz[v] = 1;
for (int u:E[v]) {
if (u==fa) continue;
dfs(u, v);
maxsub = max(maxsub, sz[u]);
sz[v] += sz[u];
}
maxsub = max(maxsub, _N-sz[v]);
if (maxsub<csize) {
center = v;
csize = maxsub;
}
}
_N-size[v]
v
注意 !
- 記得初始化
- 樹的總點數 _N 要小心,樹重心題目經常會嘗試把樹拆開或拼起來,很多時候都要重算!
- sz 陣列可以視題目需要來決定是否使用,否則可以改成使用迴傳值
練習題
- hdu6567 Cotree
- 類似 TOJ 256 (有點破梗)
給兩個樹,然後在這兩個樹中間加一條邊變成一棵樹 \(T\)
請找出怎麼加邊,會使樹 \(T\) 的點距離總和最小


樹點距離總和
定義樹 \(T\) 兩點 \(u,v\) 的距離為 \(d(u,v)\)
樹距離總和 \(S\) 為
$$S=\frac{1}{2}\sum\limits_{u,v\in T}d(u,v)$$
要怎麼計算這東西 ?

樹點距離總和
Hint : 計算每一條邊會被經過幾次
對於每一條邊 = 左邊有多少點 x 右邊有多少點
樹點距離總和
定義 \(s_r(v)\) 為以 \(r\) 為根時, \(v\) 子樹的大小
樹距離總和 \(S\) 有
$$S=\frac{1}{2}\sum\limits_{u,v\in T}d(u,v)=\sum\limits_{v \in T} s_r(v) \times (n-s_r(v))$$
long long ans = 0;
long long sol(int v, int fa) {
long long sum = 1;
for (int u:E[v])
if (u!=fa)
sum += sol(u, v);
ans += sum * (N-sum);
return sum;
}回到題目
- 加一條邊連接兩樹,這一個新的樹距離總和怎麼算
總和 = 原來樹裡面的兩兩總和 + 跨過連接線的兩兩總和
\(S\)
\(T\)
(左邊所有點-S) - 連接線 - (T-右邊所有點)
每條新的配對新增
起點到 S 的距離 + \(1\) + 終點到 T 的距離
\(S\)
\(T\)
\(S\)
\(T\)
總距離 = 左樹到S的總距離 x 右樹到T的總距離 + 左樹大小 x 右樹大小
重心到所有點距離總和最短 !
\(S,T\) 是(在原來樹上的)重心時,答案最小 !
#include <bits/stdc++.h>
using namespace std;
int N;
vector<int> E[100001];
int count(int v, int fa) {
int sum = 1;
for(int u:E[v])
if (u!=fa)
sum += count(u, v);
return sum;
}
int sz[100001];
int center, csize; // csize = INT_MAX; for init
// ensure _N is how many node of the tree
void dfs(int v, int fa, int _N) {
int maxsub = 0;
sz[v] = 1;
for (int u:E[v]) {
if (u==fa) continue;
dfs(u, v, _N);
maxsub = max(maxsub, sz[u]);
sz[v] += sz[u];
}
maxsub = max(maxsub, _N-sz[v]);
if (maxsub<csize) {
center = v;
csize = maxsub;
}
}
long long ans = 0;
long long sol(int v, int fa) {
long long sum = 1;
for (int u:E[v])
if (u!=fa)
sum += sol(u, v);
ans += sum * (N-sum);
return sum;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> N;
for(int i=0;i<N-2;++i) {
int x, y;
cin >> x >> y;
E[x].emplace_back(y);
E[y].emplace_back(x);
}
vector<int> centers;
memset(sz, -1, sizeof(sz));
for(int i=1;i<=N;++i) {
if (sz[i] == -1) {
csize = INT_MAX;
dfs(i,i, count(i,i));
centers.emplace_back(center);
}
}
assert(centers.size() == 2);
E[centers[0]].emplace_back(centers[1]);
E[centers[1]].emplace_back(centers[0]);
ans = 0;
sol(1,1);
cout << ans << '\n';
return 0;
}Centroid Decomposition
(樹)重心分解

樹重心分解 - 將一個樹重新組裝 !
重心分解樹 \(T_{CD}\) 定義如下
- 樹根是原來樹的重心
- 兒子是子樹的重心分解樹樹根

樹重心分解 - 性質 1
重心分解樹 \(T_{CD}\) 樹高為 \(O(\log n)\)

樹重心分解 - 性質 2
重心分解樹 \(T_{CD}\) 如果移除樹根
子樹的組成成員與原樹一樣

樹重心分解 - 性質 3
如果 \(c\) 是 \(a,b\) 在 \(T_{CD}\) 的最近共同祖先 (LCA) ,則
在原樹上 \(a\) 到 \(b\) 必通過 \(c\)
CF 342E. Xenia and Tree
給一個藍色的樹,有兩個操作
-
update(a) 把 a 塗成紅色
-
query(a) 問離 a 最近的紅色點距離是多少
重心分解樹
- 解決 一對全 的樹問題
- 根據 性質 3 ,一個點 \(a\) 到任意點 \(b\) 必經過
\(c=\operatorname{lca}_{T_{CD}}(a,b)\)
如果 \(c\) 是 \(a,b\) 在 \(T_{CD}\) 的最近共同祖先 (LCA) ,則
在原樹上 \(a\) 到 \(b\) 必通過 \(c\)

我們可以把問題變成
\(a\) 到 \(c\) 再到 \(c\) 子樹其他點
重心分解樹

把 \(a\) 到所有點變成
\(a\) 到 \(c\) 再到 \(c\) 子樹其他點
對於 \(T_{CD}\) 上的每個點,紀錄他到到他子樹的答案是多少
對於每一個查詢枚舉中繼點 \(c\) 組合答案
因為 \(T_{CD}\) 的高度只有 \(O(\log n)\)
因此只需要檢查\(O(\log n)\) 個中繼點 !
Try it !
- 別搞錯你現在再使用什麼樹 ! 是原來的,還是分解完的
Tree Diameter
樹直徑
直徑
圖的直徑,為圖上最長的最短距離
因為樹的最短距離唯一
因此樹的直徑就是最遠兩個點的距離
\(\operatorname{diam}(G)=\max\limits_{u, v \in G} \operatorname{dist}(u, v)\)
樹直徑演算法
- 如果邊長皆為正數:構造法 (兩次 DFS)
- 如果邊長沒有限制正負:動態規劃
構造法
定理
若樹邊權皆非負整數,
從任意點出發,所能到達的最遠點為直徑的某一端點。
證明 - 反證法
- 設出發點為 \(x\),最遠點為 \(r\),直徑端點是 \(d, d'\)
- 當中 \(\operatorname{dist}(x,r)>\operatorname{dist}(x,d)\geq \operatorname{dist}(x,d')\)
Case 1. x 交於 d-d' 連線
x
r
d
d'
很明顯的, \(r\) 比 \(d'\) 更適合當直徑端點
\(\operatorname{dist}(d,d') < \operatorname{dist}(r,d') \)
或
\(\operatorname{dist}(d,d') < \operatorname{dist}(r,d) \)
x
r
d
d'
Case 2-1. x,r 不交於 d-d' 連線
x
r
d
d'
\(r\) 比 \(d'\) 更適合當直徑端點
\(\operatorname{dist}(d,d') < \operatorname{dist}(r,d') \)
\(\operatorname{dist}(x,d) < \operatorname{dist}(x,r) \)
\(\because\) 綠 > 紅 + 黃
\(\therefore\) 綠 + 紅 > 黃
Case 2-2. x 不交於 d-d' 連線
x
r
d
d'
\(r\) 比 \(d'\) 更適合當直徑端點
\(\operatorname{dist}(d,d') < \operatorname{dist}(r,d') \)
\(\operatorname{dist}(x,d) < \operatorname{dist}(x,r) \)
\(\because\) 綠 > 紅 + 黃
\(\therefore\) 綠 + 紅 > 紅 + 黃
樹直徑構造法
- 根據定理,從任意點出法找最遠點即為直徑端點 \(d\)
- 再從找到的端點 \(d\) 找最遠點,經過的路徑即為直徑。
int fv, fd;
void dfs(int v, int pa, int d) {
if (d > fd) {
fd = d;
fv = v;
}
for (int u:V[v])
if (u!=pa)
dfs(u, v, d+1);
}
int diam() {
fd = -1;
dfs(0, 0, 0);
fd = -1;
dfs(fv, fv, 0);
return fd;
}動態規劃法
- 構造法的缺陷是邊長需為非負整數,否則證明是錯的
- 紅色線長度要大於 0
- 紅色線長度要大於 0
- 使用動態規劃可以直接求無限制條件下的解
設 \(d[x]\) 表示以 \(x\) 為根子樹的最深深度
\(d[x] = \max\limits_{u \in \text{child of } x} 1 + d[u]\)
動態規劃法
設 \(d[x]\) 表示以 \(x\) 為根子樹的最深深度
\(d[x] = \max\limits_{u \in \text{child of } x} 1 + d[u]\)
一個樹的直徑長就是枚舉 \(x\) ,取最長深度 + 次長深度 (若存在) 的最大值
x
d
d'
int dp[100000][2]; // dp 維護前兩大的深度
void push(int *a, int v) { // 單純的插入排序
if (v > a[1]) a[1] = v;
if (a[1] > a[0]) swap(a[1], a[0]);
}
int ans;
void dfs(int v, int pa) {
dp[v][0] = dp[v][1] = 0;
for (int u:V[v]) {
if (u == pa) continue;
dfs(u, v);
push(dp[v], 1 + dp[u][0]);
}
ans = max(ans, dp[v][0] + dp[v][1]);
}
int diam() {
ans = 0;
dfs(0, 0);
return ans;
}直徑的性質
- 以直徑中點為根的樹,樹高最小
- 以重心為根的樹,最大子樹最小
- 以重心為根的樹,最大子樹最小
-
所有直徑共用中點
- 反證法
- 否則就可以透過新交點構造比直徑更長的路
一般而言,直徑常用於在樹上構造路徑
練習題
- ZJ b967: 第 4 題 血緣關係 (裸題)
練習題
URAL 1752 Tree 2
給一個大小為 \(n\) 的樹 ,有 \(Q\) 次詢問
每次詢問點 \(v\) ,輸出任意一個與 \(v\) 距離為 \(d\) 的點。
Hint : \(v\) 能到的最遠點為樹直徑的端點
練習題
URAL 1752 Tree 2
給一個大小為 \(n\) 的樹 ,有 \(Q\) 次詢問
每次詢問點 \(v\) ,輸出任意一個與 \(v\) 距離為 \(d\) 的點。
Hint : \(v\) 能到的最遠點為樹直徑的端點
答案比然出現在 \(v\) 往樹直徑端點的路上,
因此求往樹直徑端點恰 \(d\) 步的點是什麼就好
紅字作法於 LCA 篇章提到
練習題
Problem : 101 - 捷運路線


Hint
- 圖 (樹) 上任兩最長路徑,必交一點 / 邊
- 反證法,否則就能構造更長的路徑
x
d
d'
y
d
d'
捷運路線 - 題解
- 很顯然的,\(L=1\) 時,答案就是樹直徑。
- 透過前面性質,構造 \(L=2\) 的答案,第二條線穿越直徑達案不會比較差
- 把直線拆解成兩段到達樹直徑的線段。
- 把直線拆解成兩段到達樹直徑的線段。
- 以次類推,把樹按深度剖分,選擇較長的鏈使用即可。
一般的樹鏈剖分是按子樹大小剖分
Lowest Common Ancestor
最近共同祖先
定根
給一個隨便的無根樹很麻煩,所以我們隨便挑一個點當作根
最近共同祖先 LCA
定義:在有根樹上,點 \(x,y\) 往 root 的最短路徑上,第一個相遇的點
\(\operatorname{lca}(x,y)\)
\(x\)
\(y\)
樹上兩點間詢問
如果詢問的答案可以透過扣除來調整,可以考慮用 LCA
ex 兩點間最短路徑長
$$\operatorname{dist}(x,y) = \operatorname{dist}(r,x)+\operatorname{dist}(r,y)-2\times \operatorname{dist}(r,\operatorname{lca}(x,y))$$
倍增法
求一個點的\(2^k\)祖先是哪一點,使用DP來完成
定義dp[i][j]表示點i的第\(2^j\)個祖先節點是誰
$$dp[i][j]=\begin{cases}-1 & \text{not exist} \\ fa(i)&j=0\\dp[dp[i][j-1]][j-1]&dp[i][j-1]\neq -1\end{cases}$$
LCA DP
for (int i=0; i<lgN; ++i)
for (int x=0; x<n; ++x)
{
if (P[x][i]==-1) P[x][i+1] = -1;
else P[x][i+1] = P[P[x][i]][i];
}
要先用 dfs 求 dp[i][0] 的答案
Jump
使用動態規劃,可以在 \(O(\log |V|)\) 的時間求出 \(v\) 的任意遠祖先
把移動距離二進位分解
再移動即可
int jump(int x,int d)
{
for(int i=0;i<lgN;++i)
if( (d>>i)&1 )
x=dp[x][i];
return x;
}LCA
使用 DP 表格 + Jump 求 LCA
int find_lca(int a,int b){
if(dep[a]>dep[b])
swap(a,b);
b=jump(b,dep[b]-dep[a]);
if(a==b)
return a;
}Step 1. 調整深度
把a,b移動到相同深度的位置去
如果移動完a=b就完成
LCA
使用 DP 表格 + Jump 求 LCA
int find_lca(int a,int b){
if(dep[a]>dep[b])
swap(a,b);
b=jump(b,dep[b]-dep[a]);
if(a==b)
return a;
for(int i=MAX_LOG;i>=0;--i)
{
if(dp[a][i]!=dp[b][i])
{
a=dp[a][i];
b=dp[b][i];
}
}
}Step 2. 二分搜
k 由大到小跳 \(2^k\) 步
如果是同樣的點,就不動,不然就跳上去
LCA
使用 DP 表格 + Jump 求 LCA
int find_lca(int a,int b){
if(dep[a]>dep[b])
swap(a,b);
b=jump(b,dep[b]-dep[a]);
if(a==b)
return a;
for(int i=MAX_LOG;i>=0;--i)
{
if(dp[a][i]!=dp[b][i])
{
a=dp[a][i];
b=dp[b][i];
}
}
return dp[a][0];
}Step 3.完成
最後會停再 LCA 下方
丟回 dp 的答案即可
練習題
- ZJ c495: 四、次小生成樹(SBMST)
一些定理 @
倍增法的優點
- 可以簡單的在樹上往 root 移動任意步
- 可以順便做 dp
樹上詢問
你得到了一棵 N 個節點的樹!! (頂點編號 1~N)
你選定了一個起點 S 跟一個終點 T,
現在你從 S 走到 T,請求出走第 K 步時走到的點。
( K=0 表示還待在 S )。
TIOJ 1687
Tarjan 的離線 LCA 演算法
\(O(n+Q)\) 一次算完
預備工具:路徑壓縮的 disjoint set
Tarjan 的離線 LCA 演算法
- 把詢問放在節點上,在 DFS 的過程中,維護可能的 LCA 找出答案
int x, y, N, Q;
vector<tuple<int,int>> query[100]; // (另一點, 答案放置位置)
vector<int> V[100];
int ans[100];
cin >> N >> Q;
for (int i = 0; i < N; ++i) {
cin >> x >> y;
V[x].emplace_back(y);
V[y].emplace_back(x);
}
for (int i = 0; i < Q; ++i) {
cin >> x >> y;
query[x].emplace_back(y, i);
query[y].emplace_back(x, i);
}Tarjan 的離線 LCA 演算法
- 如果 \(r\) 是點 \(a,b\) 的 lca,則此樹的中序走訪會依序走過 \(a, r, b\)
- 當然的 \(a, b\) 順序未知,設 \(a\) 先走
r
a
b
Tarjan 的離線 LCA 演算法
r
a
b
採用前序走訪 (進入就先標記該點)
Tarjan 的離線 LCA 演算法
r
a
b
採用前序走訪 (進入就先標記該點)
dfs 某一子樹 \(a\),把該子樹合併到 \(r\)
Tarjan 的離線 LCA 演算法
r
a
b
採用前序走訪 (進入就先標記該點)
dfs 某一子樹 \(a\),把該子樹合併到 \(r\)
如果要查詢的另一點沒被看過,就不做事
Tarjan 的離線 LCA 演算法
r
a
b
採用前序走訪 (進入就先標記該點)
dfs 某一子樹 \(a\),把該子樹合併到 \(r\)
如果要查詢的另一點沒被看過,就不做事
dfs 某一子樹 \(b\),把該子樹合併到 \(r\)
Tarjan 的離線 LCA 演算法
r
a
b
採用前序走訪 (進入就先標記該點)
dfs 某一子樹 \(a\),把該子樹合併到 \(r\)
如果要查詢的另一點沒被看過,就不做事
dfs 某一子樹 \(b\),把該子樹合併到 \(r\)
如果要查詢的另一點看過了,LCA 就是他的 disjoint set 的頭
void dfs(int v, int pa) {
used[v] = true;
for (int u : V[v]) {
if (u == pa)
continue;
dfs(u, v);
// 這裡的合併要保證 head 就是 lca
head[find(u)] = v;
}
for (auto [u, i] : query[v])
if (used[u])
ans[i] = find(u);
}r
a
b
void dfs(int v, int pa) {
used[v] = true;
for (int u : V[v]) {
if (u == pa)
continue;
dfs(u, v);
// 這裡的合併要保證 head 就是 lca
head[find(u)] = v;
}
for (auto [u, i] : query[v])
if (used[u])
ans[i] = find(u);
}int head[100]; // disjoint set
int find(int x) {
if (head[x] == x)
return x;
return head[x] = find(head[x]);
}這裡的 find 因合併較特殊
分析後是平攤 \(O(1)\)
整體複雜度 \(O(n+Q)\)
樹序列化
樹序列化
- 又稱作樹壓平
- 在進階資料結構中,有提到很多處理一維序列的方法
- 如果不知道Tree的問題怎麼解,是否有辦法把樹轉成一維序列?
歐拉走訪
- 沿著樹的邊緣走一圈
- DFS進去與出來都看一次

- 走訪結果

\(\{1,2,5,2,6,2,7,2,1,3,1,4,1\}\)
- 重要性質
一個點進去與出來構成的區間,包含子樹的所有點
能把問題轉換成 RMQ 問題!
歐拉走訪
Lowest Common Ancestor
最近共同祖先
更神奇的作法
- 可以做到\(O(n)\)預處裡,\(O(1)\)查詢
Method of Four Russians
4個俄羅斯人法(!?),把\(O(\log n)\)壓到\(O(1)\)的技巧
LCA與樹序列化

| 點 | 1 | 2 | 5 | 2 | 6 | 2 | 7 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 深度 | 0 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 0 |
LCA與樹序列化

| 點 | 1 | 2 | 5 | 2 | 6 | 2 | 7 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 深度 | 0 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 0 |
A與B的LCA是:
第一個A與最後一個B構成的區間中,深度最小的點
區間最小值
| 點 | 1 | 2 | 5 | 2 | 6 | 2 | 7 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 深度 | 0 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 0 |
觀察到剛剛的特性後,就能把LCA問題變成RMQ問題
不過有學過\(O(n)\)預處裡\(O(1)\)查詢的資料結構嗎?
Sparse Table
- 可以在\(O(n\log n)\)預處理,\(O(1)\)查詢的資料結構
st[x][y] = \(a_x\)到\(a_{x+2^y-1}\)的答案(共\(2^y\)個元素)
查詢任意範圍a~b,只要查詢
$$\min\begin{cases} st[a][c] \\ st[b-2^c][c]\end{cases} ,c=\lfloor\log_2(b-a+1)\rfloor$$
c=std::__lg(b-a+1);
騙我!
- 這方法沒有\(O(n)\)預處裡阿!
- 別急,還有其他方法
建表法
- 因為數列相鄰的數字只有\(+1,-1\)兩種可能
- 可以考慮數列的差分序列
| 點 | 1 | 2 | 5 | 2 | 6 | 2 | 7 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 深度 | 0 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 0 |
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 |
建表法
- 對於一個差分序列還原出來的原始數列,最小值的位置是固定的!結果與原數列無關
若\(a,b,c,d,e\)的差分序列是
\(<1,-1,-1,-1,>\)
最小值一定是\(e\)
建表法
- 預先把所有可能的差分序列最小值的位置建表
- 因為差分序列只有兩種數字,可以用二進位表示
\(O(n2^n)預處裡\)
\(O(1)查詢\)
看起來超級爛?

分塊大法
- 如果把數列每\(K\)個資料切一塊,預先算出每一塊的最小值
\(O(\frac{n}{K}+K)\)找出最小值
\(O(n)\)預處裡
| 點 | 1 | 2 | 5 | 2 | 6 | 2 | 7 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 深度 | 0 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
|---|

分塊大法+Sparse Table
- 把大塊的資料做Sparse Table,就能在\(O(1)\)時間算大塊最小值
\(O(1+K)\)找出最小值
\(O(\frac{K}{n}\log \frac{K}{n} +n)\)預處裡
| 0 | 1 | 1 | 1 | 0 |
|---|
分塊大法+Sparse Table+建表法
- 把小塊的資料做建表法,就能在\(O(1)\)時間算小塊最小值
\(O(1+1)\)找出最小值
\(O(\frac{K}{n}\log \frac{K}{n} + K2^K+ n)\)預處裡
| 點 | 1 | 2 | 5 | 2 | 6 | 2 | 7 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 深度 | 0 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 0 |
數學的時間
\(O(\frac{K}{n}\log \frac{K}{n} + K2^K+ n)\)
K要怎麼設才能讓複雜度變好?
數學的時間
\(O(\frac{K}{n}\log \frac{K}{n} + K2^K+ n)\)
\(K=c\log n\)
數學的時間
\(O(\frac{K}{n}\log \frac{K}{n} + K2^K+ n)\)
\(K=c\log n\)
\(\frac{K}{n}\log \frac{K}{n}\\=\frac{c\log n}{n}\log \frac{c\log n}{n}\\=\frac{c\log n}{n}(\log{c\log n}-\log{n})=o(n)\)
\(O\)表示小於等於的話,\(o\)就表示小於
數學的時間
\(O(\frac{K}{n}\log \frac{K}{n} + K2^K+ n)\)
\(K=c\log n\)
\(K2^K\\=c\log{n}2^{c\log{n}}=c\log{n}2^{\log{n^c}}\\=c\log{n}\times n^c\)
數學的時間
\(O(\frac{K}{n}\log \frac{K}{n} + K2^K+ n)\)
\(K=c\log n\)
\(c\log{n}\times n^c\)
設\(c=0.5\)
\(0.5\log{n}\sqrt{n}\leq 0.5\sqrt{n}\sqrt{n}\in O(n)\)
LCS
分塊大法+Sparse Table+建表法
- 把K設為\(0.5\log{n}\)
\(O(1)\)找出最小值
\(O(n)\)預處裡
樹鏈剖分
樹鏈剖分
- 利用尤拉路徑做序列化,能解決子樹有關的問題
- 但是樹上任意路徑詢問的問題就比較麻煩了
- 樹鏈剖分是另一種把樹轉換成序列操作的方法

樹序列化-樹鏈剖分
把樹分解成許多線段,查詢時把幾個線段上的答案合併
要怎麼切線段?
Robert Tarjan's
Heavy Light Decomposition
- 將非葉節點的點,選擇重邊連結
- 其餘的邊為輕邊,會被分解掉
輕重邊
- 重邊:最多子節點子樹的邊
- 輕邊:不是重邊的邊

輕重邊

- 重邊:最多子節點子樹的邊
- 輕邊:不是重邊的邊
樹鏈剖分
- 有了輕重鏈分解之後,將重邊連接的所有連續的點放到資料結構上,就完成了!

How to coding
- 樹鏈剖分是一個用說的比較簡單的方法
- 但是實作細節繁複,因此考驗選手 coding
debug能力 - 合理的切分步驟有助於降低實作複雜度
- 準備資料結構:要把問題轉成哪種一維資料結構
- 蒐集資訊:利用 dfs 計算樹鏈剖分需要的資訊
- 重新編號 : 利用第一步的資訊,把點重新邊號,放到資料結構上
- 開始爬樹 !
預備工作
準備你會的資料結構
BIT / 線段樹 / Treep
不會的話先回去學資料結構...
樹練剖分 step 1
利用 dfs 計算出必要資訊
- 每一個點的子樹大小
- 最大的子樹是哪一個方向
- 深度
- 父節點是誰
後面步驟忘了什麼東西幾乎都加在這一步
struct info{
int w;
int dep;
int pa;
int size;
int next;
int id;
int root;
} inf[100001];
樹鏈剖分 step 1
int prepare(int v, int pa, int d=0)
{
int maxsub = 0;
inf[v].pa = pa;
inf[v].dep = d;
inf[v].size = 1;
inf[v].next = -1;
for(int u:E[v])
{
if (u==pa) continue;
int sub = prepare(u, v, d+1);
inf[v].size += sub;
if ( sub > maxsub ) {
maxsub = sub;
inf[v].next = u;
}
}
return inf[v].size;
}樹鏈剖分 step 2
- 透過前步驟的資訊找到重鏈,把點重新邊號到資料結構上
- 同一條重鏈邊號連續

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
樹鏈剖分 step 3
int mid = 1;
void mapTo(int v, int pa, int root)
{
inf[v].id = mid++;
inf[v].root = root;
seg.update(inf[v].id, inf[v].w);
if (inf[v].next!=-1)
mapTo(inf[v].next, v, root);
for(int u:E[v])
{
if (u==pa) continue;
if (u==inf[v].next) continue;
mapTo(u, v, u);
}
}對於每一個點
紀錄他所在的重鏈頭是誰
樹鏈剖分 step 4
- 爬樹 ! 單點修改
要記得要改在 新邊號 的位置上!
void update(int s, int w)
{
inf[s].w = w;
seg.update(inf[s].id, inf[s].w);
}
樹鏈剖分 step 4
- 爬樹 ! 區間修改 / 詢問
有兩種 case
- 頭尾剛好在同一個重鏈上
直接算!
-
頭尾在不同重鏈上
慢慢爬樹,直到變 case 1
樹鏈剖分 step 4
- 爬樹 ! 區間修改 / 詢問
頭尾在不同重鏈上
S
T
樹鏈剖分 step 4
- 爬樹 ! 區間修改 / 詢問
頭尾在不同重鏈上
S
T
如果不同鏈,先算 root 最深的鏈
樹鏈剖分 step 4
- 爬樹 ! 區間修改 / 詢問
頭尾在不同重鏈上
S
T
如果不同鏈,先算 root 最深的鏈
樹鏈剖分 step 4
- 爬樹 ! 區間修改 / 詢問
頭尾在不同重鏈上
S
T
算完,把點移動到鏈 root 的 parent
樹鏈剖分 step 4
- 爬樹 ! 區間修改 / 詢問
頭尾在不同重鏈上
S
T
如果不同鏈,先算 root 最深的鏈
樹鏈剖分 step 4
- 爬樹 ! 區間修改 / 詢問
頭尾在不同重鏈上
S
T
如果不同鏈,先算 root 最深的鏈
樹鏈剖分 step 4
- 爬樹 ! 區間修改 / 詢問
頭尾在不同重鏈上
S
T
算完,把點移動到鏈 root 的 parent
樹鏈剖分 step 4
- 爬樹 ! 區間修改 / 詢問
頭尾在不同重鍊上
S
T
在同一條鏈,直接算!
樹鏈剖分 step 4
重點
- 因為重鏈上編號連續,可以用 RMQ 來處理
- 往上爬行時,深的重鏈先處理,直到頭尾在同一重鏈
- 如果資料在邊上面,可以轉換為在點上面處理
每個點記錄 自己到 parent 的邊
u
e
v : 紀錄 e 的資料
int query(int s, int t)
{
int ans = 0;
while( inf[s].root != inf[t].root )
{
if (inf[inf[s].root].dep < inf[inf[t].root].dep)
swap(s, t);
ans = margeans(ans, seg.query(inf[s].id, inf[inf[s].root].id));
s = inf[s].root;
s = inf[s].pa;
}
ans = margeans(ans, seg.query(inf[s].id, inf[t].id) );
return ans;
}樹鏈剖分
- 每一個點到 root 最多只會經過 \(\log n\) 條重鏈
- 因此任兩點間查詢最多只會做 \(O(\log n)\) 次的 RMQ
- 若單次 RMQ 需要 \(O(\log n)\) 的時間
樹鏈剖分提供了 \(O(\log^2 n)\) 的方法來計算樹路徑的問題
樹鏈剖分
- 子樹修改:因為編號按照 DFS 的順序編號
子樹的編號範圍有連續性 ! 因此可以直接區間修改
樹鏈...剖分...
- 大部分..RMQ..問題...都能..搬到...樹上...再出...一次...
- 常數...肥大...慎用...
Directed Acyclic Graph
有向無環圖
DAG
DAG 有向無環圖,它的性質與他的名子一樣
- 是一張有向圖
- 沒有環

討論圖論最重要的兩個特例
Tree
DAG
DAG
DAG 也有與 Tree 深度類似的特性
因為沒有環,從一個點出發後必定不會回到自己
如果一個問題計算的步驟先後順序恰好是 DAG,就容易規劃計算順序

Topological Ordering
如果對於每一個事件 x 要進行前,要先做 a,b,c...
是否能規畫一個合理的執行順序 ?
b 之前要先做 a
c 之前要先做 a
d 之前要先做 a b c
e 之前要先做 a c d

e

完成拓譜排序後
所有邊都只會由前面的點指向後面的點
Topological Sort
DAG 的拓譜排序相當的簡單

e
使用一個 Queue 來記錄那些點的條件已經滿足了
為了方便,用一個陣列 indeg
紀錄一個點還有多少條件未達成
Topological Sort

e
步驟1. 計算所有點的 indeg
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 1 | 1 | 3 | 3 |
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 1 | 1 | 3 | 3 |
| a |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 1 | 1 | 3 | 3 |
| a |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 1 | 1 | 3 | 3 |
| a |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 2 | 2 |
| a |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 2 | 2 |
| b | c |
|---|
| a |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 2 | 2 |
| c |
|---|
| a | b |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 2 |
| c |
|---|
| a | b |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 2 |
| c |
|---|
| a | b |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 2 |
| a | b | c |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| a | b | c |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| d |
|---|
| a | b | c |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| a | b | c | d |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| a | b | c | d |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| e |
|---|
| a | b | c | d |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| a | b | c | d | e |
|---|
Topological Sort

e
步驟1. 計算所有點的 indeg
步驟2. 把 indeg 為 0 的點放入 Queue
while Queue 非空
p = Q.front(); 輸出 p
檢查 p 的所有鄰居 v
將 v 的 indeg - 1
如果 v 的 indeg 變成 0
就把 v 放到Queue
| a | b | c | d | e |
|---|
Topological Sort

e
如果演算法結束後,沒有輸出所有點的點
有可能代表 圖不是 DAG 或 圖不連通
Topological Sort

e
除此方法之外
也能用一次 DFS 找出拓譜序 (的逆序)
方法也十分簡單
hint : 後序走訪
跳格子遊戲 TIOJ 1092
- 有兩個人 Alice, Bob 在一張 DAG 上玩遊戲
- 一開始 Alice 站在起點,接著 Bob 選擇一個與起點相鄰的點,然後再換 Alice 選下一個相鄰點,如此交替著,直到有人到達終點為止。
- 假設一定有路到達終點,如果兩人都用最佳策略玩遊戲,請問誰必勝?
跳格子遊戲 TIOJ 1092

跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
因為沒則選擇,只能選擇移動到 "先手必敗" 的狀況 (下一回合先後手交換GG)
Note : 這一個題目是 "後手做移動",如果是 "先手做移動" 結論會有點不一'樣
跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
如果只有終點 : 先手必勝
跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
只有通向必勝的路,因此必敗
跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
終點前兩步 : 有路通向必敗,因此必勝
跳格子遊戲 TIOJ 1092
KEY : 如果目前這一步是 "先手必勝"
表示不論如何移動,都會使得 "先手必敗"
以此推出所有點是必勝還是必敗
跳格子遊戲 TIOJ 1092

按照拓譜排序的逆序進行
分層圖
分層圖
- 再有全局狀態的問題下,將圖分解成數個層級,透過進入一個層級來完成狀態的改變
狀態A
狀態B
Faulty Robot (kattis)
- 有一個GG人,平時只會由 1 號點出發,沿著紅色的邊行走,直到沒有路可以走為止。
- 但是有時GG人會有Bug,會讓他最多走一次黑色的邊,給你一張圖與邊的關係,GG人可能會在那些點停下來?

建立分層圖
常見方法有
- 真的蓋好幾層,可能會MLE,方法簡單
- 類似DP,打狀態標記,要維護的東西多,容易疏忽
Faulty Robot (kattis)
沒Bug的世界
已經發生Bug的世界
黑色邊
Faulty Robot (kattis)
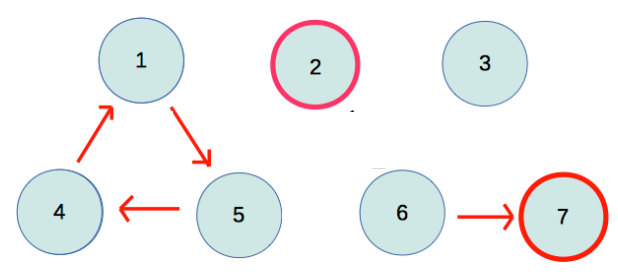

Faulty Robot (kattis)


More practice : uva 816
Full Tank? (kattis)
- 給定義一張有向帶權圖,有一台車要從起點開到終點
- 車子的油箱有 \(P\) 單位,每單位距離都要花費 \(1\) 單位油
- 每個點都有加油站,每單位油賣 \(c_i\) 元
- 問從起點到終點,金錢花費最小為何?
CF 786B Legacy
- 給一張神奇的有向帶權圖,這一個圖的邊描述如下
- 1 u v w : u 到 v 有一條 w 的邊
- 2 u l r w:u 到 [l,r] 有一條 w 的邊
-
3 u l r w:[l,r] 到 u 有一條 w 的邊
給定起點,問這一個點到所有點的最短路
雙向搜尋
- 有時,因為分層圖或是其他方法建圖過大,會導致可能的狀態過多,可以利用從起點、終點同時搜尋的方法,尋找中間點的位置來優化
I Puzzle You UVa 12618
- 轉魔術方塊
Flow
網路流
送貨問題
今天老師請了一些同學幫忙從 302 搬運電腦硬碟到一間儲藏室存放,每位同學一次只能拿取一顆硬碟。
因為走廊通道較狹窄小,每條走廊都有通行人數的限制。
請問每單位時間最多可以運送幾顆硬碟到倉庫 ?
求取兩點間的最大運輸量
教室
倉庫
7
6
8
3
4
3
倉庫
7
3/6
8
3/3
4
3
答案 \(=3+\)
教室
倉庫
3/7
3/6
3/8
3/3
4
3/3
答案 \(=3+3\)
教室
倉庫
3/7
6/6
6/8
3/3
3/4
3/3
答案 \(=3+3+3\)
教室
Flow 網路流
- 一張圖中兩點間的最大運輸量的問題,稱為網路流問題。
- 網路流可以結合線性代數等領域,產生不同的變化。
定義
- 網路:一張有向圖\(G=(V,E)\)
- 起點、匯點:流的起點與終點
- 容量\(C(x,y)\):邊 \(\overline{xy}\) 的最大流量
- 流量\(F(x,y)\):邊 \(\overline{xy}\) 的已使用流量
-
剩餘容量\(C_f(x,y)\):\(C(x,y)-F(x,y)\)
Flow
3/8
在圖中,使用 \(x/y\)
代表這條邊的容量 Capacity 與流量 Flow
Flow 的性質
3/8
流量不能夠超過一條邊的容量
\(C(x,y) \geq F(x,y)\)
除了起點終點,進去的流量要等於出來的流量
\(\sum_{v\in x_{in}} F(v,x) = \sum_{w\in x_{out}} F(x,w)\)
所有到 \(x\) 的邊
所有離開 \(x\) 的邊
Flow 的性質
任兩點間流量
$$F(x,y)+F(y,x)=0$$
$$F(y,x)=-F(x,y)$$
Flow 的性質
反向流 視為 正向流取負數
可行流
- 滿足前三個基本條件的流稱為可行流
- 最大流問題,即求所有可行中,最大的流量
Ford–Fulkerson Algorithm
- 簡稱 FF,於 1956 年提出解決最大流問題的演算法
不飽和邊
- 如果一條邊的流量尚未到達極限,就是不飽和邊
- 反之稱為飽和邊
5 / 6
不飽和邊,還有一單位的流量可以用
- 若從起點到匯點,存在一條由不飽和邊構成的路徑,那目前流量就不是最大流
5 / 6
1 / 3
2 / 4
但這能構成最大流嗎?
不飽和邊
因此,我們可以不斷的尋找不飽和邊的路徑,將其填充流量。
直到找不到不飽和邊路徑
3/7
6
8
3/3
3/3
3/3
不存在起點到終點的不飽和邊路徑,但不是最大流
隨意的流動可能會阻塞更多能流動的路徑
增廣路徑
- 如果隨意地找流動方向,可能會讓一些錯誤的水流堵塞道路,因此需要一個修正的機制。
- 因此可以流動的邊,不單純只是找不飽和邊而已
2/6
2
4
反向弧
- 如果有一條水流由 X 流向 Y 的流量是 2,容量是 6
- 轉換成 X 流向 Y 容量是 4,Y 往 X 流的容量是 2
6/2
0+2=2
6-2=4
反向弧
能夠把流錯的水,沿反方向推回去
1/1
0
1
反向弧
能夠把流錯的水,沿反方向推回去
反向弧
能夠把流錯的水,沿反方向推回去
0
1
反向弧
能夠把流錯的水,沿反方向推回去
0
1
反向弧
能夠把流錯的水,沿反方向推回去
1
0
對於下方的點,維持 進入 = 出來 的流量 !
反向弧
能夠把流錯的水,沿反方向推回去
1
0
對於上方的點,維持 進入 = 出來 的流量 !
1
0
1
1
1
反向弧
透過反向邊,維護最大能改變的量
在不破壞可行流的狀況下,修正答案
增廣路徑
定義能使可行流擴張的路徑,是由下兩種邊構成的路
- 不飽和邊 \(F(x,y)<C(x,y)\)
- 非 \(0\) 的反向邊 \(F(y,x)>0\)
增廣路徑最大流定理
如果圖有可行流 \(F\) 之後,找不到由起點到匯點的增廣路徑
\(\iff\)
\(F\) 是最大流
假設圖是簡單的,且所有容量皆是非負整數
Ford–Fulkerson Algorithm
int flow = 0;
while( true )
{
if( 找到增廣路 )
{
把增廣路上的流量都+1
}
else
break;
}利用 DFS 找增廣路
如果邊容量都是整數,每次答案至少會增加 \(1\)
如果邊長為小數,則無法保證答案必然可以收斂到最大流上
Ford–Fulkerson Algorithm

Wiki 的構造,FF 演算法會往 \(3+2r\) 收斂,而非最大流 \(2M+1\)
\(e_1=e_3=1\)
\(e_2=r\)
其中 \(r^2=1-r\)
其餘為 \(M\geq 2\)
Internet Bandwidth
UVA 820
求無向圖的最大流。
實作方法
- 若使用二維矩陣直接紀錄任兩點的 F/C 值是很簡單的,但空間複雜度高
- 因此範例使用相鄰串列實作
Add edge
建立邊的時候,要把反向邊一起蓋出來
方法一、用 vector 全部存在一起
方法二、存邊陣列
Vector
vector<tuple<int,int,int>> V[101];
// x=>y 可以流 C
void add_edge(int x, int y,int c)
{
V[x].emplace_back(y, c, V[y].size());
V[y].emplace_back(x, 0, V[x].size()-1);
}
多用一個參數紀錄反向邊的位置
如果 \(x\to y\) 是單向邊,反向容量是 \(0\)
如果 \(x\to y\) 是雙向邊,反向容量是 \(c\)
雙向邊如果要蓋成4條邊其實也不是不行...
Why?
邊陣列
vector<int> V[101];
vector<tuple<int,int>> E;
// x=>y 可以流 C
void add_edge(int x, int y, int c)
{
V[x].emplace_back( E.size() );
E.emplace_back(y,c);
V[y].emplace_back( E.size() );
E.emplace_back(x,0);
}反向邊的編號只要把自己的編號 xor 1 就能取得
網路演算法框架
- 網路流演算法大致上只差再怎麼找增廣路
int ffa(int s,int e)
{
int ans = 0, f;
End = e;
while(true)
{
memset(used, 0, sizeof(used));
f = dfs(s, INT_MAX); // 不同演算法找法不一樣
if( f<=0 ) break;
ans += f;
}
return ans;
}
使用 DFS 尋找增廣路
- 紀錄從起點到終點增廣路的最小值
int dfs(int v, int f)
{
if( v==End ) return f;
used[v] = true;
int e, w, rev;
for( int eid : V[v] )
{
tie(e,w) = E[eid];
if( used[e] || w==0 ) continue;
w = dfs(e, min(w,f));
if( w>0 )
{
更新流量
return w;
}
}
return 0;// Fail!
}更新流量
- \(x\to y\) 要流 \(w\):
- \(C(x,y)-=w\)
- \(C(y,x)+=w\)
if( w>0 )
{
get<1>(E[eid ]) -= w;
get<1>(E[eid^1]) += w;
return w;
}if( w>0 )
{
get<1>(t) -= w;
get<1>(V[e][rev]) += w;
return w;
}在這一個步驟要對反向邊修改
Match
Bipartite Matching
婚姻問題
- 今天有一些女生,每位女生都對一些男生有好感,今天有個好奇的戶政人員想問一些事情...
- \(A=\{a,b,d\}\)
- \(B=\{b,c\}\)
- \(C=\{a,d\}\)
- \(D=\{c,d\}\)
假設一個男生只能配一個女生,且假設一個女生只能配一個男生
婚姻問題
- 有沒有可能讓每一個女生都配對到不同的男生?
- \(A=\{a,b,d\}\)
- \(B=\{b,c\}\)
- \(C=\{a,d\}\)
- \(D=\{c,d\}\)
婚姻問題
- 最多可以產生多少配對?
- \(A=\{a,b,d\}\)
- \(B=\{b,c\}\)
- \(C=\{a,d\}\)
- \(D=\{c,d\}\)
婚姻問題
- 如果把兩人配對可以拿到紅包,怎樣配對拿到的錢最多?
- \(A=\{a,b,d\}\)
- \(B=\{b,c\}\)
- \(C=\{a,d\}\)
- \(D=\{c,d\}\)
婚姻問題
- 怎樣配對才會讓配對最幸福美滿?
- 如果配對有優先級,不會有兩人交換後有更好的答案
- \(A=\{a,b,d\}\)
- \(B=\{b,c\}\)
- \(C=\{a,d\}\)
- \(D=\{c,d\}\)
婚姻問題
- 如果沒有性別差異呢?
- \(A=\{a,b,C\}\)
- \(B=\{A,b,c\}\)
- \(C=\{a,B,d\}\)
- \(D=\{c,d\}\)
Match
- 一個圖中,選擇一些邊,使得這些邊沒有共用頂點
這樣的邊集合稱為匹配 \(M\)
紅色的邊集合是一個匹配
藍色的邊則不是
Perfect Match
- 如果所有的頂點都有被選入匹配中,該匹配是完美匹配
完美匹配不一定存在
Maximun Match
- 所有匹配中,選到的邊 (點) 數量最多的方法
交錯路徑
- 一條路,起點是匹配邊,沿著該路經過的邊匹配/非匹配交錯
OXOXO
擴張路徑
- 一條路,起點終點是非匹配邊,沿著該路經過的邊匹配/非匹配交錯
XOXOX
擴張路徑
- 跟網路流一樣
如果匹配中存在擴張路徑,就不是最大匹配
反過來說呢?
Berge’s Lemma
- 如果匹配M沒有擴張路徑\(\iff\)M是最大匹配
二分圖
- 如果可以把一張圖的點分成兩集合\(A,B\),使得所有的邊都是\(A,B\)相連,同集合內的點沒有邊的話,就是一張二分圖
Graph Coloring
UVA 193
判斷一張圖是不是二分圖
二分圖匹配問題
- 在二分圖上的匹配是容易的,可以透過較簡單的觀念來完成。
- 不是二分圖的匹配問題稱之為一般圖匹配。需要較複雜的方法。
婚姻問題
- 最多可以產生多少配對?
- \(A=\{a,b,d\}\)
- \(B=\{b,c\}\)
- \(C=\{a,d\}\)
- \(D=\{c,d\}\)
婚姻問題
- 如果把男生女生分成兩個集合,這個問題就是在求二分圖的最大匹配
- \(A=\{a,b,d\}\)
- \(B=\{b,c\}\)
- \(C=\{a,d\}\)
- \(D=\{c,d\}\)
Kőnig's theorem
- 有時稱為匈牙利演算法(比較簡單的那個)
不斷找出增廣路徑,改成交錯路徑,直到找不到為止
Kőnig's theorem
int konig()
{
memset(match,-1,sizeof(match));
int ans=0;
for(int i=1;i<=n;++i)
{
memset(used, 0, sizeof(used));
if( dfs(i) )
ans++;
}
return ans;
}Koning 透過逐一地把點加入集合中,檢查加入的新點是否構成增廣路徑
V[i] 記錄左半邊可以選擇右邊的哪些點
match[i] 記錄右半邊以配對到左半邊的哪個點
vector<int> V[205];
int match[205]; // A<=B
bool dfs(int v)
{
for(int e:V[v])
{
if( used[e] ) continue;
used[e] = true;
if( match[e]==-1 || dfs( match[e] ) )
{
match[e] = v;
return true;
}
}
return false;
}
Kőnig's theorem
Kőnig's theorem
總共要做 \(V\) 次DFS
總複雜度為 \(O(V(E+V))\)
Gopher II
UVA 10080
逃竄的地鼠問題
基於網路流的二分圖匹配
網路流可以很輕易的把二分圖問題轉換為一般的網路流問題來完成。
基於網路流的二分圖匹配
Key : 利用邊容量來限制點的度數
如果一個點要被匹配的話,只能選擇使用一條邊
基於網路流的二分圖匹配
Key : 利用邊容量來限制點的度數
超級起點
超級終點
基於網路流的二分圖匹配
Key : 利用邊容量來限制點的度數
超級起點
超級終點
1
1
1
控制左半邊deg = 1
基於網路流的二分圖匹配
Key : 利用邊容量來限制點的度數
超級起點
超級終點
1
1
1
控制左半邊deg = 1
1
1
1
控制右半邊deg = 1
基於網路流的二分圖匹配
從超級起點流到超級終點,形成的最大流就是最大匹配
超級起點
超級終點
1
1
1
1
1
1
基於網路流的二分圖匹配
網路流的二分途匹配,可以透過容量,自由地控制點能配對到的點數,甚至可以有三四層以上的關係,較前方法更活用
超級起點
超級終點
1
1
1
1
1
1
複雜度為 \(O((E+V)F)\),通常 \(F=O(V)\)
使用更好的網路流演算法 (Dinic) 可以到達 \(O(E\sqrt V)\)
經典問題
有一個 \(N\times N\) 的西洋棋盤,想在上面放一些城堡
任兩個城堡不能在同一個直排或橫排上,而且有一些格子不能放城堡,問這一個西洋棋盤最多能放幾個城堡
簡化 hdu 1045





經典問題
有一個 \(N\times N\) 的西洋棋盤,想在上面放一些城堡
任兩個城堡不能在同一個直排或橫排上,而且有一些格子不能放城堡,問這一個西洋棋盤最多能放幾個城堡
簡化 hdu 1045





如果一格城堡放在 \((a,b)\) 上,其他棋子的 \(x\) 座標就不能是 \(a\),\(y\) 座標座標就不能是 \(b\)
把座標數字當一個點
把合法座標當作邊
選擇最多邊不共用頂點
二分圖
最大匹配!
UVa 11419





有一個 \(N\times M\) 的棋盤,上面放了 \(P\) 個棋子,每一次可以選擇一個直排或是一個橫排,把選擇到的那整排上面的棋子都拿走,問最少要幾次才能拿完所有棋子
把座標數字當一個點
把合法座標當作邊
選擇最少點
使得所有邊都至少有一個端點被選中
最小點覆蓋
最小點覆蓋數 = 2 (綠色點)
最小點覆蓋數 = 2 (綠色點)
定理 1. Kőnig's theorem 二分圖上
最小點覆蓋數 \(c\) = 最大匹配數 \(M\)
Prove
顯然的 \(c\geq M\)
因為匹配的每一個邊都不共用頂點
所以至少要 \(M\) 個點
如果能找到一個構造方法
恰好用 \(M\) 個點覆蓋全部邊
就證明完畢了
Hint: 利用匈牙利演算法
定理 1. Kőnig's theorem 二分圖上
最小點覆蓋數 \(c\) = 最大匹配數 \(M\)
TOPC 2020 G
給一個 \(n\times m\) 的格子花園,一些格子太溼不能種仙人掌,其他格子可以種仙人掌,但任兩個仙人掌不能相鄰。
求最多可以種幾棵仙人掌,並且把種植的方法輸出。





Hint : 相鄰的格子黑白交錯塗色
=> 二分圖 !
TOPC 2020 G
給一個 \(n\times m\) 的格子花園,一些格子太溼不能種仙人掌,其他格子可以種仙人掌,但任兩個仙人掌不能相鄰。
求最多可以種幾棵仙人掌,並且把種植的方法輸出。





Hint : 相鄰的格子黑白交錯塗色
=> 二分圖 !
選最多的點
使得點都不相臨
(一個邊只有一端點被選到)
最大點獨立集
最大點獨立集數 = 4 (橘色點)
定理 2. 二分圖上
最大點獨立集 \(P\) = 總點數 \(n-\) 最大匹配數 \(M\)
定理 3. (補充) 二分圖上
最大團 \(C\) = 補圖最大獨立集 \(M\)
最大獨立集 : 任兩點兩兩不相臨
最大團 : 任兩點兩兩相臨
補圖 :
有邊變成沒邊
沒邊變成有邊
DAG 的最小邊覆蓋問題
今天有一個有向無環圖 (DAG)
有一些人要在 DAG 上跑步
任兩人跑步路徑不能相交
如果要讓 DAG 所有的頂點都被經過一遍,最少要幾人
hint 對每一個點 \(v\) 建立 \(v_{in}, v_{out}\)
=> 二分圖
HW
Flow
FF的優化
Ford–Fulkerson Algorithm
- 複雜度為\(O(E|F|)\)
- 在解決二分圖匹配時,因為 \(F\) 最多是 \(V/2\),在簡單的題目複雜度通常是好的
- 大學比賽不適用
- 大學比賽不適用
- 在其他狀況呢?
1000000000
1000000000
1000000000
1000000000
1
1000000000
1000000000
1000000000
1000000000
1
\(F=1\)
1000000000
1000000000
1000000000
1000000000
1
\(F=2\)
1000000000
1000000000
1000000000
1000000000
1
\(F=3\)
經過很久以後
1000000000
1000000000
1000000000
1000000000
1
\(F=2000000000\)
Ford–Fulkerson Algorithm
FFA隨意地亂找道路,不一定每次都挑到適合的道路
要如何改進?
Edmonds–Karp algorithm
用BFS找增廣路徑
int flow = 0;
while( true )
{
if( BFS 找到增廣路 )
{
擴充增廣路上的流量
}
else
break;
}Edmonds–Karp algorithm
用 BFS 找增廣路徑,每次的增廣路路徑長都是最短的
如果找到長度是 P 的路,那就不存在比 P 更短的增廣路
每一次更新,至少讓一個點 BFS 距離變遠
\(O((E+V)EV)=O(E^2V)\)
Edmonds–Karp algorithm
- \(O(E^2V)\)覺得還是不妙,還可以近一步優化嗎?
Dinic's algorithm
- 先對增廣路徑做 BFS 標距離
- 利用 BFS 找出來的距離,由近到遠找增廣路徑
int flow = 0;
while( 做出 BFS 層次圖 )
{
while( 在 BFS 層次圖 找到增廣路 )
{
擴充增廣路上的流量
}
}7
6
8
3
4
3
7
6
8
3
4
3
做BFS層次圖
深度0
深度1
深度2
6
8
3
3
層次圖由淺到深找Flow
深度0
深度1
深度2
7
3/6
8
3/3
4
3
7
3/6
8
3/3
4
3
做BFS層次圖
深度0
深度1
深度2
深度3
3/7
3/6
3/8
3/3
4
3/3
層次圖由淺到深找Flow
深度0
深度1
深度2
深度3
3/7
6/6
6/8
3/3
3/4
3/3
層次圖由淺到深找Flow
深度0
深度1
深度2
深度3
3/7
6/6
6/8
3/3
3/4
3/3
已經沒有到終點的路,結束
Dinic's algorithm
- BFS 層次圖到終點的短路徑是嚴格遞增的,因此最多做 \(V\) 次 BFS
- 在層次圖中,如果一個點找不到流,這個點就不會再被用到
- 對於每個層次圖可以在 \(O(VE)\) 的時間找完所有的增廣路
- 對於每個層次圖可以在 \(O(VE)\) 的時間找完所有的增廣路
- 總複雜度為\(O(V^2E)\)
Dinic's algorithm
- 如果圖是一張單位容量網路 (每條邊容量一樣) Dinic的複雜度是
$$O(\operatorname{min}(V^{2/3},E^{1/2})\times E)$$
故使用Dinic解二分圖最大匹配複雜度是\(O(E\sqrt{V})\)
比 Kőnig 或一般 Flow \(O(EV)\)快
特例
Dinic
- Dinic主體
int dinic(int s,int e)
{
int ans = 0, f;
End = e;
while(bfs(s))
{
while( f = dfs(s, INT_MAX) )
ans += f;
}
return ans;
}Dinic
- BFS打標記
int End, dist[101];
bool bfs(int s) {
memset(dist, -1, sizeof(dist));
queue<int> qu;
qu.emplace(s);
dist[s]=0;
while( !qu.empty() ) {
int S = qu.front(); qu.pop();
for(auto &p : V[S]) {
int E, C;
tie(E, C, ignore) = p;
if( dist[E]==-1 && C!=0 ) {
dist[E]=dist[S]+1;
qu.emplace(E);
}
}
}
return dist[End] != -1;
}Dinic
- DFS找路徑
int dfs(int v, int f) {
int e,w,rev;
if( v==End || f==0 ) return f;
for( auto &t : V[v] )
{
tie(e,w,rev) = t;
if( dist[e]!=dist[v]+1 || w==0 )
continue;
w = dfs(e, min(w,f));
if( w>0 )
{
get<1>(t) -= w;
get<1>(V[e][rev]) += w;
return w;
}
}
dist[v] = -1; //優化,這個點沒用了
return 0;// Fail!
}費用流
- 如果每一條邊流過 1 單位都要收一點錢
- 那請問達成最大流時,花費最小是多少 ?
網路流原來是單純用 dfs / bfs 找通路
改成用 最短路徑 找通路就是最小費用流!
邊的長度 = 費用
因為有負邊問題,只能使用 SPFA 等來找最短路
二分圖的最大權匹配
- 全國賽好像出現過幾次的防破台題
- 普遍的解法有兩種
- Kuhn–Munkres Algorithm (匈牙利演算法)
- 轉成費用流
一般圖的最大匹配
Match for general graph
一般圖與二分圖的差異
一般圖存在奇環,二分圖全為偶環
奇環使反轉操作受到限制
在二分圖中,如果遇到可以匹配的新點,就會把路徑反轉
奇環使反轉操作受到限制
在一般圖中,配對兩點不保證可以二分,會產生矛盾
GG
交錯樹
- 將DFS深度為奇數標記為奇點,偶數標記為偶點形成的樹
- 二分圖上的 Match 必然是 偶點-奇點 的配對


定義Root是偶點
交錯樹
- 將DFS深度為奇數標記為奇點,偶數標記為偶點形成的樹
- 一般圖上的 Match 必然是可能會有偶點 - 偶點配對
定義Root是偶點
Edmonds's Blossom algorithm
花被演算法
Blossom algorithm
因為花被的英文 Perianth 生澀
所以 Edmonds 使用 Blossom 來借代
花被算法提供了一個解決奇環的方法
假定所有的Match都是由偶點出發的
大陸奇怪翻譯:帶花樹算法!?
縮花定理
- 考慮一個有奇環的交錯樹
Root
縮花法
- 考慮一個有奇環的交錯樹
Root

縮花法
Root
找完奇環的Match後,收縮奇環到Root成為新圖
Root
縮花法性質
- 收縮完的Root是偶點,即整個環都是偶點
- 即所有點都可以當配對起點的意思
