String
大綱
- Implementation
- Regex
- Trie
- Match Algorithm
- KMP 演算法
- Z algorithm
- Rolling hash
- 字串術語定義
- 前綴:包含開頭的連續子字串
- abc 的前綴有
- a, ab, abc
- abc 的前綴有
-
後綴:包含結尾的連續子字串
-
abc 的後綴有
- c, bc, abc
-
abc 的後綴有
- 前綴:包含開頭的連續子字串
Ad Hoc
格式化輸入問題
實作能力
字串的基本問題,大部分都是實作問題
熟悉自己使用的語言工具以及技巧相當重要
不同程式語言的解法可以相差很多...
string s = "abcd";
// 反轉 "dcba"
reverse(s.begin(), s.end());
// 修改 "dcca"
s[2] = 'c'; s = "abcd"
# 反轉 "dcba"
s = s[::-1]
# 修改 "dcca"
s = s[:2]+'c'+s[3:]
# 常用方法
x = list(s)
x[2] = 'c'
s = ''.join(x)正規(Regular)形式輸入
- 給定的輸入是一種正規 (Regular) 形式
- 一般現代的程式語言都有內建函數能快速處理這類型的資料
Example
時間 02:23 = 兩個數字 + 冒號 + 兩個數字
日期 2/3 = 一或兩個數字 + 斜線 + 一或兩個數字
note : 這部分等於 "Formal Language" 這門選修課教的正規語言
正規 (Regular) 形式
- 不是所有規則都能被稱為 正規(regular) 的,正規的規則只能由以下組成
- 空字串 \(\lambda\) 是正規的
- 單一一個字母是正規的
Example
兩個數字 + 冒號 + 兩個數字
一或兩個數字 + 斜線 + 一或兩個數字
正規 (Regular) 形式
- 不是所有規則都能被稱為 正規(regular) 的,正規的規則只能由以下組成
- 空字串 \(\lambda\) 是正規的
- 單一一個字母是正規的
- (正規 或 正規) 是 正規的
Example
數字 = 0 或 1 或 2 或 3 ... 或 9
正規 (Regular) 形式
- 不是所有規則都能被稱為 正規(regular) 的,正規的規則只能由以下組成
- 空字串 \(\lambda\) 是正規的
- 單一一個字母是正規的
- (正規 或 正規) 是 正規的
- 正規 + 正規 是 正規的
Example
兩位數字 = 數字 + 數字
正規 (Regular) 形式
- 不是所有規則都能被稱為 正規(regular) 的,正規的規則只能由以下組成
- 空字串 \(\lambda\) 是正規的
- 單一一個字母是正規的
- (正規 或 正規) 是 正規的
- 正規 + 正規 是 正規的
- 正規 的 Kleene * 是 正規的 (0 ~ 無限多次相加)
Example
\(\{a\}^*=\{\lambda, a, aa, aaa, \cdots\}\)
一些數字 = 數字* = \(\{0\sim 9\}^*\) = \(\{0,1,\cdots ,9, 00,01, \cdots\}\)
正規語言的讀取
- 整理出規則之後,基本上有兩種處理方法
1. 寫對應的自動機 (根據規則,暴力解析)
2. 利用正規表達式,套函數處理 ( regex )
自動機
- 自動機 相當於 根據讀入的字是什麼,就做什麼事情的程式

(有點有邊 : 可以出成圖論問題)
自動機
- 考看你寫 code 功力好不好...
讀一個整數
讀一個字元
讀一個整數
#include <bits/stdc++.h>
using namespace std;
char buf[256];
int idx;
int getInt() {
int res = 0;
while (isdigit(buf[idx])) {
res = res * 10 + (buf[idx] - '0');
idx++;
}
return res;
}
int getChar() {
return buf[idx++];
}
int main() {
while (cin.getline(buf, 256)) {
idx = 0;
int hh = getInt();
int c = getChar();
int mm = getInt();
cout << "now : " << hh << ' ' << mm << endl;
}
}
一些實作要點
- 絕大多數的字串分切都要根據 "下一個字是什麼" 才能決定
- ex. 讀入數字要遇到 "不是數字" 的東西才知道數字結束了
- ex. 讀入數字要遇到 "不是數字" 的東西才知道數字結束了
- 雖然 C/C++ 都有把讀取來的資料還回去的方法,但常數很大 ,建議不要用
- ungetc()
- cin.unget()
- 因此強烈建議要用 getline 全部讀入字串後再慢慢處理
| 1 | 2 | + |
|---|
scanf
- scanf 能作 "有限的" 的正規語言讀取
- 實務上夠應付常見狀況了
#include <bits/stdc++.h>
using namespace std;
int main() {
int hh, mm;
while (~scanf("%d:%d", &hh, &mm)) {
cout << "now : " << hh << ' ' << mm << endl;
}
}
sscanf
char str[] = "12:30";
int hh, mm;
// 用法與 scanf 一樣
sscanf(str, "%d:%d", &hh, &mm);Wonderful sscnaf Down the Rabbit-Hole
int main() {
char str[] = "123 456 789";
char *ptr = str;
int val;
while ( sscanf(ptr, "%d", &val) == 1) {
cout << val << '\n';
// move ptr to next integer
ptr++; // space
while (isdigit(ptr[0])) ptr++;
}
}
輸出 :
123 456 789
一個討厭 strtok 的人,寫的字串分割
該程式的運行時間複雜度為何
Wonderful sscnaf Down the Rabbit-Hole
int main() {
char str[] = "123 456 789";
char *ptr = str;
int val;
while (sscanf(ptr, "%d", &val) == 1) {
cout << val << '\n';
// move ptr to next integer
ptr++; // space
while (isdigit(ptr[0])) ptr++;
}
}
一個討厭 strtok 的人,寫的字串分割
該程式的運行時間複雜度為何
因為紅色部分,最多只會執行 str 那麼多的長度,所以整體下來是 \(O(n)\)
Time Limit Exceeded

int main() {
char str[] = "123 456 789";
char *ptr = str;
while (sscanf(str, "%d", &val) == 1);
}
int
sscanf(const char *ibuf, const char *fmt, ...) {
// ...
ret = vsscanf(ibuf, fmt, ap);
// ...
}int
vsscanf(const char *inp, /**/) {
// ...
int inr = strlen(inp);
// ...
}
Apple 的鍋 ?
- 只是因為 GCC 的實作理解難度更高的問題...
int main() {
char str[] = "123 456 789";
char *ptr = str;
while ( sscanf(str, "%d", &val) == 1);
}
__sscanf (const char *s, const char *format, ...)
{
FILE *f = _IO_strfile_read (&sf, s);
}_IO_strfile_read (_IO_strfile *sf, const char *string)
{
_IO_str_init_static_internal (sf, (char*)string, 0, NULL);
}_IO_str_init_static_internal (_IO_strfile *sf, char *ptr /**/)
{
end = __rawmemchr (ptr, '\0');
}RAWMEMCHR (const void *s, int c) {
// ...
return (char *)s + strlen (s);
}
int main() {
char str[] = "123 456 789";
char *ptr = str;
int val;
while ( sscanf(ptr, "%d", &val) == 1) {
cout << val << '\n';
// move ptr to next integer
ptr++; // space
while (isdigit(ptr[0])) ptr++;
}
}
當你以為你漂亮均攤的時候
sscanf 再搞你
所有常用的編譯器附帶的 sscanf 都會對 ptr 做 strlen
不管有沒有用到所有字元

希望你不是最後一個踩到雷點的人...
自從去年發生 GTA 5 優化事件後,越來越多人知道這個小知識
Good Luck!
regex (C++11)
- C++11 有提供的 正規表達式 函數庫可以使用
#include <bits/stdc++.h>
#include <regex>
using namespace std;
int main() {
int hh = 0, mm = 0;
string buf;
regex rule("([0-9]*):([0-9]*)");
smatch res;
while (getline(cin, buf)) {
regex_match(buf, res, rule);
hh = stoi(res[1]);
mm = stoi(res[2]);
cout << "now : " << hh << ' ' << mm << endl;
}
}
C++ regex 語法
- 非常的攏長 @ ,這裡只挑常用的給大家
- a : 要配對一個 a
-
[expr] : 要配對一個東西
- [a-z] : 要配對一個小寫字母
- [a-zA-Z] : 要配對一個字母
- a* : 要配對 a 重複 0 ~ 無限多次
- a+ : 要配對 a 重複 1 ~ 無限多次
- a? : 要配對 a 重複 0 ~ 1次
- a|b : 要配對 a 或是 b
-
(a)
- 規則順序括號
- 有配對成功,就把括號裡的東西存起來
Example
配對時間
時間 = 整數 + : + 整數
regex rule("([0-9]*):([0-9]*)");整數是很多個 0-9 組成的東西 ,使用 [0-9]* 來表示
Example
regex rule("([0-9]*):([0-9]*)");
smatch res;
regex_match(buf, res, rule);
// res[0] = "12:30"
hh = stoi(res[1]); // 12
mm = stoi(res[2]); // 30res 是一個 smatch 的物件 (可以把它當作 vector 看)
res[0] 永遠存放被匹配的整體 (整個字串)
自訂的括號要從 1 開始拿 !
例題 UVA 494
一個文章裡面有幾個單字 ?
單字 = 連續的英文字母
用任何你喜歡的方法寫吧 !
正規形式的字串處理
| 暴力 | 正規表達式 | scanf | |
|---|---|---|---|
| 簡潔度 | 看自己能力 | 簡單,但要背很多語法 | 簡單通用,但遇到特殊格式無法處理 |
| 速度 | 看自己能力 | O(n) 常數稍大 | 跟 IO 一樣 |
後記
- 正規表達式有很多工具要記憶,使用得宜可以避免一些實作失誤的問題
- 正規語言參考練習網站
- RegexOne - Learn Regular Expressions - Lesson 1: An Introduction, and the ABCs
#include <regex>
regex rule("([0-9]*):([0-9]*)");
smatch res;
regex_match(buf, res, rule);
// res[0] = "12:30"
hh = stoi(res[1]); // 12
mm = stoi(res[2]); // 30import re
rule = re.compile(r'([0-9]*):([0-9]*)')
m = rule.match("12:30")
# m.group(0)= "12:30"
hh = int(m.group(1)); // 12
mm = int(m.group(2)); // 30其他練習題
- Parse
- UVA 1200
- UVA 620
-
不會正規表達式就有點機車的題目
- UVA 325
Trie
字典樹
String Data Search
如同一般的數字一樣,有些問題需要再一群字串中查詢特定的字串存不存在
但是不同於數字,數字默認可以 \(O(1)\) 比對資料
然而字串比較需要逐字元比對,需要花費更多的時間
因此需要設計一個更好的資料結構來加速比較的時間
Trie
- 雖然最初的發明者 Edward Fredkin 把他讀做 tree
- Trie is a tree.
- 但是 Tree (樹) 也是重要的資料結構,發音易混淆,所以後人把讀音改成 try
- 中文譯為 字典樹
\(\{"ant", "cat", "can"\}\)
a
c
a
n
t
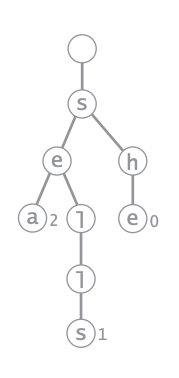
Trie
- 字典樹的邊表示一個字母,如果到該節點已經有單字組成了,則在節點做標記
\(\{"ant", "cat", "can","c"\}\)
a
c
a
n
t
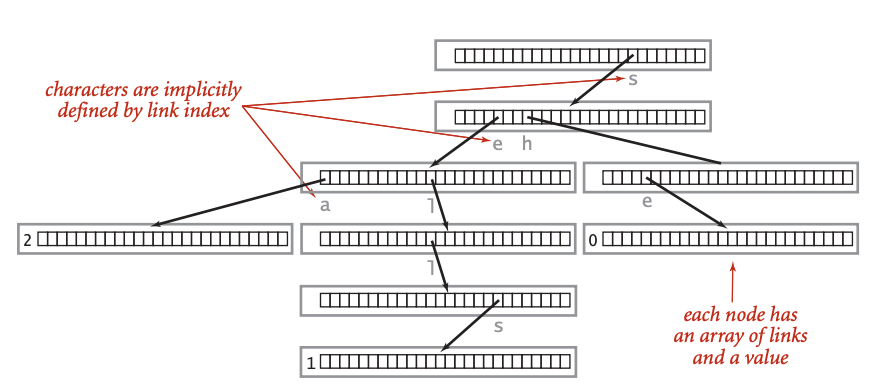
struct node {
int hit = 0;
node *next[26] = {}; // a-z
};Trie 插入 / 搜尋
- 就沿著邊走下去而已... 複雜度都是 \(O(|S|)\)
using pnode = node *;
pnode insert(const char *s, pnode root) {
if (!root)
root = new node;
if (s[0] == '\0') {
root->hit++;
} else {
root->next[*s-'a']
= insert(s+1, root->next[*s-'a']);
}
return root;
}一般而言,為了省空間,會把字母投射到 0~26 之類的位置。
前頁 Hack
-
設 s 是 const char * 的變數
-
s+1 : 取 s 去除第一個字元的後綴 (s[1:]) -
*s : 等於 s[0]
如果對二重指標熟的話,程式可以更簡單
void insert(const char *s, pnode *root) {
if (!*root)
*root = new node;
if (s[0] == '\0') {
(*root)->hit++;
} else {
insert(s+1, &(*root)->next[*s-'a']);
}
}
Trie
- 如果預先把 \(k\) 個字串 \(S_1, S_2\cdots S_k\) 建立成 Trie
- 複雜度 \(O(\sum |S|)\)
- 對於一個字串 \(T\),查詢
- 是否有 \(T=S_n\)
- 有多少 \(S_n\) 等於 \(T\) 的某一個前綴
-
T=apple, S=app
-
- 複雜度都是 \(O(T)\)
- 複雜度 \(O(\sum |S|)\)
- 此外自動機演算法大多都基於 Trie 來改造,是很重要的基本資料結構
最後...
Trie 其實很 月半... 空間用量要小心

練習題
- CSES - Word Combinations @
- 給你一個大字串跟一些小字串
- 問有幾種組合方法,可以把小字串串接成大字串
#include <bits/stdc++.h>
using namespace std;
const int mod = 1'000'000'007;
struct node {
int hit = 0;
node* next[26] = {}; // a-z
};
using pnode = node *;
pnode insert(const char *s, pnode root) {
if (!root)
root = new node;
if (s[0] == '\0') {
root->hit++;
} else {
root->next[*s-'a'] = insert(s+1, root->next[*s-'a']);
}
return root;
}
int main() {
int k;
pnode root = new node;
string base, tmp;
cin >> base;
cin >> k;
while (k--) {
cin >> tmp;
root = insert(tmp.data(), root);
}
vector<int> dp(base.size() + 1, 0);
dp[0] = 1;
for (size_t i=1 ; i<=base.size() ; ++i) {
int len = 0;
pnode ptr = root;
const char *str = base.c_str() + (i-1);
while (*str) {
ptr = ptr->next[*str-'a'];
len++;
if (!ptr) break;
if (ptr->hit) {
dp[i-1+len] += dp[i-1];
dp[i-1+len] %= mod;
}
str++;
}
}
cout << dp.back() << '\n';
}
特殊題型 01-Trie
- 通常是求一些數字跟 xor 有關的問題
- 我們可以把 數字 當作是 由 0 或 1 組成的 二進位字串,以便使用 Tire 維護
HDU4825
給一個數字集合,詢問數字 s 與集合內的哪一個數字 xor 起來最大
洛谷P4551
問一個有權重的樹,所有路徑中,權重 xor 最大值為何
常見的字串演算法
String Match
KMP Algorithm
String Match
- 檢查輸入 \(T\) 包含是否包含字串 \(S\) 。
String Match
- 檢查輸入 \(T\) 包含是否包含字串 \(S\) 。
ex. 哪一些字串包含 "apple"
pineapple
application
thisisanapplepie
懶人法
- 如果不統計出現次數,可以使用內建函數
#include <bits/stdc++.h>
using namespace std;
int main() {
string T = "This is a string with an apple.";
string S = "apple";
if (auto res = T.find(S); res != string::npos) {
cout << "found " << S << " at " << res << '\n';
}
char Tc[] = "This is C-style string with an Egg.";
char Sc[] = "Egg";
if (auto res = strstr(Tc, Sc); res != nullptr) {
cout << "found " << Sc << " at " << res - Tc << '\n';
}
}複雜度 : 規格不保證
最簡單方法 \(O(|T||S|)\)
// O(S*T)
for (int i=0;i<TSize-SSize+1 ++i)
if (strncmp(S, T, SSize) == 0)
return true;
return false;小秘密
- gcc 實作的 strstr 是 \(O(n)\) 的 @
/* Fast strstr algorithm with guaranteed linear-time performance.
Small needles up to size 3 use a dedicated linear search. Longer needles
up to size 256 use a novel modified Horspool algorithm. It hashes pairs
of characters to quickly skip past mismatches. The main search loop only
exits if the last 2 characters match, avoiding unnecessary calls to memcmp
and allowing for a larger skip if there is no match. A self-adapting
filtering check is used to quickly detect mismatches in long needles.
By limiting the needle length to 256, the shift table can be reduced to 8
bits per entry, lowering preprocessing overhead and minimizing cache effects.
The limit also implies worst-case performance is linear.
Needles larger than 256 characters use the linear-time Two-Way algorithm. */
char *
STRSTR (const char *haystack, const char *needle)
另一個小秘密
- gcc 實作的 string::find 是 \(O(n^2)\) 的 @
- 跟前面很爛的方法是同一個...
while (__len >= __n)
{
// Find the first occurrence of __elem0:
__first = traits_type::find(__first, __len - __n + 1, __elem0);
if (!__first)
return npos;
// Compare the full strings from the first occurrence of __elem0.
// We already know that __first[0] == __s[0] but compare them again
// anyway because __s is probably aligned, which helps memcmp.
if (traits_type::compare(__first, __s, __n) == 0)
return __first - __data;
__len = __last - ++__first;
}
return npos;
}// O(S*T)
for (int i=0;i<TSize-SSize+1;++i)
if (strncmp(S, T, SSize) == 0)
return true;
return false;
String Match
線性匹配演算法
Knuth–Morris–Pratt Algorithm
直接比較
A
P
P
L
E
ex. 哪一些字串包含 "apple"
pineapple
application
thisisanapplepie
The others (failed path)
\(\phi\)
bool test() {
char S[] = "apple";
char T[] = "thisisanapplepie";
int hit = 0;
int succ = strlen(S);
for (char c : T) {
if (c == S[hit]) hit++;
else hit = 0;
if (hit == succ) return true;
}
return false;
}難道 \(O(n)\) 的演算法這麼簡單?
一個 字串 直直比過去就好 ?
bool test() {
char S[] = "apple";
char T[] = "thisisanapplepie";
int hit = 0;
int succ = strlen(S);
for (char c : T) {
if (c == S[hit]) hit++;
else hit = 0;
if (hit == succ) return true;
}
return false;
}反例
P
P
A
P
\(\phi\)
PPAPMAN
PPPAPMAN (失敗 !)
| P | P | P | A | P | M |
| P | P | A | P |
原來的方法遇到失敗時,直接重頭來過
漏掉了 "存在其他位置的配對依然正確" 的可能性
for (char c : T) {
if (c == S[hit]) hit++;
else hit = 0; // 不應該總是歸 0 !!
if (hit == succ) return true;
}| P | P | A | P |
| P | P | A | P |
共同前後綴
- 在 \(T\) 中尋找 \(S\) ,兩字串已知共同前綴部分為 \(R\) (紅色部分)
abaaba
abaaba............
abaabc
S:
T:
如果 \(R\) 中,存在一個不等於 \(R\) 的前綴等於後綴
abaab
abaab
abaaba............
abaabc
S:
T:
abaabc
把 \(S\) 往後移動 \(|R|\) 的距離也有機會產生匹配
共同前後綴
abaaba............
abaabc
S:
T:
abaabc
一個字串可能有很多共同前後綴
abaaba?
abaaba
abaaba
為了要避免遺漏可能性,我們只能往前移動最少的步伐
也就是使用次長前後綴作為往前移動的根據
最接近的復原方法
在發生錯誤返回跳回之前,我們希望可以檢查
當前 "已配對的部分" 是否能 "繼續利用"。
ABCDXXXABCD?
ABCDXXXABCD?
如果已配對的字串存在一個 開頭 等於 結尾 的部分
發生配對錯誤時,應該找到 次長的 開頭 等於 結尾 的部分來重新嘗試
最長的 開頭 = 結尾 就是字串本身
ABCDXXXABCDX
次長共同前後綴 DP
- 我們可以使用動態規劃來解出每一個前綴的次長前後綴長度
定義 \(dp[n]\) 表示:
字串 \(s_0s_1\cdots s_n\) 的次長前後綴 終點位置
此外定義 \(dp[0]=-1\),表示答案不存在
次長共同前後綴 DP
- 我們可以使用動態規劃來解出每一個前綴的次長前後綴長度
定義 \(dp[n]\) 表示:
字串 \(s_0s_1\cdots s_n\) 的次長前後綴 終點位置
也就是
字串 \(s_0s_1\cdots s_n\) 的開頭 \(dp[n]+1\) 個字與結尾 \(dp[n]+1\) 個字一樣
此外定義 \(dp[0]=-1\),表示答案不存在
0123456789
ABCDXXXABC
定義 \(dp[n]\) 表示:
字串 \(s_0s_1\cdots s_n\) 的開頭 \(dp[n]+1\) 個字與結尾 \(dp[n]+1\) 個字一樣
\(dp[9]=2\)
因為紅字處是一樣的
\(dp[3]=-1\)
不存在答案
此外定義 \(dp[0]=-1\),表示答案不存在
次長共同前後綴 DP
計算 \(dp[n]\) 有 \(3\) 種可能
01234567890
ABCXXXXABZA
1. 如果 \(dp[n-1]=-1\)
\(\Rightarrow\) 直接檢查 \(s[n]\) 與 \(s[0]\) 是否一樣即可
\(dp[9] = -1\)
\(dp[10]\) 直接比較字串開頭
次長共同前後綴 DP
計算 \(dp[n]\) 有 \(3\) 種可能
01234567890
ABCDXXXABCD
2. 如果 \(s[n]\) 等於 \(s[dp[n-1]+1] \)
\(\Rightarrow dp[n]=dp[n-1]+1\)
\(dp[9] = 2\) (紅橘)
\(dp[10]=dp[9]\) + 綠色
次長共同前後綴 DP
計算 \(dp[n]\) 有 \(3\) 種可能
01234567890
ABADXXXABAB
3. 如果 \(s[n]\) 不等於 \(s[dp[n-1]+1] \)
\(\Rightarrow\) 透過 \(s[0:dp[n-1]]\) 的次長前後綴繼續檢查
\(dp[9] = 2\)
\(dp[2] = 0\)
ABCABD.....ABCABA
\(dp[n-1] = 4\)
ABCAB
\(dp[4] = 2\)
橘色 = 橘色,紅色 = 紅色
ABCABD.....ABCABA
ABCABD.....ABCABA
如果比較 \(s[dp[n-1]+1]\) 失敗了
就遞迴比較 \(s[dp[dp[n-1]]+1]\)
void build(const char *s) {
dp[0] = -1;
for (int i=1; s[i] ; ++i) {
int len = dp[i-1];
while (last != -1) {
if (s[i] == s[len+1]) break;
else len = dp[len];
}
if (s[i] == s[len+1]) dp[i] = len + 1;
else dp[i] = -1;
}
}len 表示目前已知最長的次長前後綴範圍
void build(const char *s) {
dp[0] = -1;
for (int i=1; s[i] ; ++i) {
int len = dp[i-1];
while (len != -1) {
if (s[i] == s[len+1]) break;
else len = dp[len];
}
if (s[i] == s[len+1]) dp[i] = len + 1;
else dp[i] = -1;
}
}時間複雜度
上程式的時間複雜度為和 ?
for (int i=1; s[i] ; ++i) {
int len = dp[i-1];
while (len != -1) {
if (s[i] == s[len+1]) break;
else len = dp[len];
}
if (s[i] == s[len+1]) dp[i] = len + 1;
else dp[i] = -1;
}
時間複雜度
可以發現,在第 i 次迴圈
while 的執行次數不超過 dp[i-1] 次
for (int i=1; s[i] ; ++i) {
int len = dp[i-1];
while (len != -1) {
if (s[i] == s[len+1]) break;
else len = dp[len];
}
if (s[i] == s[len+1]) dp[i] = len + 1;
else dp[i] = -1;
}
時間複雜度
可以發現,在第 i 次迴圈
while 的執行次數不超過 dp[i-1] 次
while 每執行一次,len 至少要 -1
for (int i=1; s[i] ; ++i) {
int len = dp[i-1];
while (len != -1) {
if (s[i] == s[len+1]) break;
else len = dp[len];
}
if (s[i] == s[len+1]) dp[i] = len + 1;
else dp[i] = -1;
}
時間複雜度
可以發現,在第 i 次迴圈
while 的執行次數不超過 dp[i-1] 次
while 每執行一次,len 至少要 -1
len 最小只能是 -1
for (int i=1; s[i] ; ++i) {
int len = dp[i-1];
while (len != -1) {
if (s[i] == s[len+1]) break;
else len = dp[len];
}
if (s[i] == s[len+1]) dp[i] = len + 1;
else dp[i] = -1;
}
時間複雜度
可以發現,在第 i 次迴圈
while 的執行次數不超過 dp[i-1] 次
while 每執行一次,len 至少要 -1
len 最小只能是 -1
len 只有在第 9 行會增加
for (int i=1; s[i] ; ++i) {
int len = dp[i-1];
while (len != -1) {
if (s[i] == s[len+1]) break;
else len = dp[len];
}
if (s[i] == s[len+1]) dp[i] = len + 1;
else dp[i] = -1;
}
時間複雜度
可以發現,在第 i 次迴圈
while 的執行次數不超過 dp[i-1] 次
while 每執行一次,len 至少要 -1
len 最小只能是 -1
len 只有在第 9 行會增加
len 最多只會增加 \(O(n)\) 次
for (int i=1; s[i] ; ++i) {
int len = dp[i-1];
while (len != -1) {
if (s[i] == s[len+1]) break;
else len = dp[len];
}
if (s[i] == s[len+1]) dp[i] = len + 1;
else dp[i] = -1;
}
時間複雜度
可以發現,在第 i 次迴圈
while 的執行次數不超過 dp[i-1] 次
while 每執行一次,len 至少要 -1
len 最小只能是 -1
len 只有在第 9 行會增加
len 最多只會增加 \(O(n)\) 次
因為扣除次數的不能比增加的次數多,
因此 while 的執行次數只能跟 len 增加的次數一樣多,
因此總複雜度為 \(O(n)\)
練習題
基本應用
CSES - String Matching
CSES - Finding Borders
找循環
CSES - Finding Periods
UVA 10298 - Power Strings
UVA 455 - Periodic Strings
Booth's algorithm (找 s 與 s 後綴 KMP dp 變化的關係)
CESE - Minimal Rotation
Hint
設一個字串 \(P\) 由 \(n\) 個 \(Q\) 串接
\(P=\underbrace{QQ\cdots QQ}_{n個}\)
那麼 P 的次長共同前後綴是
\(\underbrace{QQ\cdots QQ}_{n-1個}\)
KMP Algorithm
- 算完了次長共同前後綴,要怎麼找 \(T\) 裡面有沒有 \(S\) ?
KMP Algorithm
- 算完了次長共同前後綴,要怎麼找 \(T\) 裡面有沒有 \(S\) ?
把字串串接成 \(T' = S@T\),\(@\) 是不存在 S,T 中的一個字
然後做 DP ,如果過程中 DP 的值等於 \(|S|-1\) ,就找到了
ppap@pppapman
int dp[100];
void build(const char *s) {
dp[0] = -1;
for (int i=1; s[i] ; ++i) {
int last = dp[i-1];
while (last != -1) {
if (s[i] == s[last+1]) break;
else last = dp[last];
}
if (s[i] == s[last+1]) dp[i] = last + 1;
else dp[i] = -1;
}
}
bool find(const char *s, const char *t) {
int hit = -1;
for (int i=0; t[i] ; ++i) {
while (hit != -1) {
if (t[i] == s[hit+1]) break;
else hit = dp[hit];
}
if (t[i] == s[hit+1]) hit = hit + 1;
else hit = -1;
if (s[hit+1] == '\0') return true;
}
return false;
}分開寫的版本,兩邊其實一樣,但找的那邊不用記錄 dp 的結果,直接放在 hit 。
UVa 11475
- 給你一個字串,問這一個字串"結尾"要增加幾個字,才能變成回文
Hint
- 變成回文 : 字串 \(Q\) + 反過來的字串 \(Q'\)
- \(Q, Q'\), 最多能重疊的長度 ?
- 想想看 \(Q' @ Q\) 的次長共同前後綴 !
String Match
Gusfield’s algorithm
Gusfield’s algorithm
- 又稱 Z Algorithm ,拓展 KMP
- 與 KMP 很像,但是 函數 定義的不一樣
\(Z[x]\) : 表示 \(s[x:]\) 與 \(s\) 共同前綴的長度
| A | B | A | B | A | A | B |
|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 1 | 2 | 0 |
定義 \(Z[0] = 0\)
\(Z[2] = 3\) ,因為 \(s[2:] = \) ABAAB ,與整個字串 ABABAAB 開頭三個字一樣
使用 Gusfield’s algorithm 找配對
- 把字串串接成 \(S@T\),\(@\) 是不存在 S,T 中的一個字
然後做 Z algorithm ,如果過程中 Z algorithm 的值等於 \(|S|\) ,就找到了
這兩個演算法能做的事情差不多,但處理的方向不一樣,可以視需求來決定用哪一個
Z Index
- 要能使用演算法,我們必須要先求出 \(Z[x]\)
\(Z[x]\) : 表示 \(s[x:]\) 與 \(s\) 共同前綴的長度
| A | B | A | B | A | A | B |
|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 1 | 2 | 0 |
定義 \(Z[0] = 0\)
Z Index
- 要能使用演算法,我們必須要先求出 \(Z[x]\)
Z Index 的演算法關鍵是 :
透過一對 L, R 來表示\(s[L, R]\) 字串開頭相同
| A | B | A | B | A | A | B |
|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 1 | 2 | 0 |
L=2
R=4
Z Index
- 要能使用演算法,我們必須要先求出 \(Z[x]\)
Z Index 的演算法關鍵是 :
透過一對 L, R 來表示\(s[L, R]\) 字串開頭相同
那根據 \(i\) 是否在 \(L,R\) 之間,有 3 種可能
| A | B | A | B | A | A | B |
|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 0 | 1 | 2 | 0 |
L=2
R=4
Z Index
- 1. \(i\) 不在 \(L, R\) 之間
那這一個 \(L, R\) 一點用也沒有,暴力求答案 !
並且把 \(L, R\) 更新成暴力求出來的範圍
L=R=0;
for (int i=1; s[i];++i) {
if (R < i) {
while (s[z[i]] == s[i+z[i]])
z[i]++;
L = i;
R = i + z[i] - 1;
}
}Z Index
- 2. \(i\) 在 \(L, R\) 之間,且 \(i + z[i-L] - 1< R\)
那 \(z[i]=z[i-L]\)
L
R
\(i\)
Z Index
- 2. \(i\) 在 \(L, R\) 之間,且 \(i + z[i-L] -1 < R\)
L
R
根據定義,紅色等於紅色
\(i\)
\(i-L\)
所以要算 \(Z[i]\),可以參考 \(Z[i-L]\)
那 \(z[i]=z[i-L]\)
Z Index
- 2. \(i\) 在 \(L, R\) 之間,且 \(i + z[i-L] -1< R\)
L
R
根據定義,紅色等於紅色
\(i\)
\(i-L\)
所以要算 \(Z[i]\),可以參考 \(Z[i-L]\)
\(i+z[i-L]-1\)
根據 \(Z[i-L]\) 可以知道黃色的部分也相等
那 \(z[i]=z[i-L]\)
Z Index
- 2. \(i\) 在 \(L, R\) 之間,且 \(i + z[i-L] -1< R\)
L
R
根據定義,紅色等於紅色
\(i\)
\(i-L\)
所以要算 \(Z[i]\),可以參考 \(Z[i-L]\)
\(i+z[i-L]-1\)
根據 \(Z[i-L]\) 可以知道黃色的部分也相等
如果黃色的最右邊 \(i+z[i-L]-1 < R\) 答案就能直接用了!
那 \(z[i]=z[i-L]\)
Z Index
- 3. \(i\) 在 \(L, R\) 之間,且 \(i + z[i-L] -1\geq R\)
L
R
\(i\)
\(i-L\)
\(i+z[i-L]-1\)
因為黃色區塊一樣,因此前 \(R-i+1\) 個字已經判斷過了,不用重新判斷是否相等!
最後更新 L,R 的範圍 !
那暴力找 \(z[i]\) ,但是黃色區域不用檢查
void ZAlgo(const char *s) {
int L, R;
vector<int> z(strlen(s));
L=R=0;
for (int i=1; s[i]; ++i) {
if (R < i) {
z[i] = 0;
while (s[z[i]] == s[i+z[i]])
z[i]++;
L = i;
R = i + z[i] - 1;
} else if ( i + z[i-L] - 1 < R) {
z[i] = z[i-L];
} else {
z[i] = R - i + 1;
while (s[z[i]] == s[i+z[i]])
z[i]++;
L = i;
R = i + z[i] - 1;
}
}
}可以發現 case 1,3 基本上是一樣的,只有起始點不一樣,所以可以合在一起寫 (只判斷case 2 )
void ZAlgo(const char *s) {
int L, R;
vector<int> z(strlen(s));
L=R=0;
for (int i=1; s[i]; ++i) {
if ( i <= R && i + z[i-L] - 1 < R) {
z[i] = z[i-L];
} else {
z[i] = max (0, R - i + 1);
while (s[z[i]] == s[i+z[i]])
z[i]++;
L = i;
R = i + z[i] - 1;
}
}
}精簡版 Z Algorithm
此處運算有負數
R 或 i 的型態不可以是unsigned (ex. size_t)
void ZAlgo(const char *s) {
int L, R;
vector<int> z(strlen(s));
L=R=0;
for (int i=1; s[i]; ++i) {
if ( i <= R && i + z[i-L] - 1 < R) {
z[i] = z[i-L];
} else {
z[i] = max (0, R - i + 1);
while (s[z[i]] == s[i+z[i]])
z[i]++;
L = i;
R = i + z[i] - 1;
}
}
}時間複雜度分析
一樣有雙層迴圈,複雜度是多少呢 ?
void ZAlgo(const char *s) {
int L, R;
vector<int> z(strlen(s));
L=R=0;
for (int i=1; s[i]; ++i) {
if ( i <= R && i + z[i-L] - 1 < R) {
z[i] = z[i-L];
} else {
z[i] = max (0, R - i + 1);
while (s[z[i]] == s[i+z[i]])
z[i]++;
L = i;
R = i + z[i] - 1;
}
}
}時間複雜度分析
如果執行一次 while 迴圈,R 就會增加 1
R 最大只會是 \(n\)
因此 while 總共只會執行 \(O(n)\) 次
總時間複雜度是 \(O(n)\)
練習題
- 把 KMP 的題目用 Z 再寫一遍
- HDU - 6153 A Secret
- 給兩個字串 S,T ,問 S 的每一個後綴在 T 出現的次數
- 給兩個字串 S,T ,問 S 的每一個後綴在 T 出現的次數
- CSES - Longest Palindrome
- Manacher Algorithm
- 設回文長度為奇數
- 把字串的每一個字中間補上特殊自元
-
abac => #a#b#a#c#
-
- 把字串的每一個字中間補上特殊自元
- 設 \(M[x]\) 為以 \(x\) 為中心的回文長度
- 其餘部份與 Z algorithm 一樣
- 設回文長度為奇數
- Manacher Algorithm
Hash
雜湊
Hash
- 透過某種函數,為資料建立特徵的方法
- 一般而言,特徵的資料量會比原始資料小,因此能用於加速計算
Raw
HashCode
Hash
Hash
- 設雜湊函數為 \(H(x)=h\)
- 如果有 \(x\neq y\),但是\(H(x)=H(y)\) 稱為雜湊的碰撞
- 能維持雜湊的碰撞率低,且輸出資料量仍舊小的 \(H\) 越好
Raw
HashCode
Hash
比賽雜湊的應用
- C++ 內建的 unordered_set / unordered_set
- 黑魔法 (用法一樣,速度更快)
- gp_hash_table @
- Rolling Hash
unordered_set
unordered_set<int> ust;
ust.insert(71);
ust.insert(22);
if (ust.find(22) == ust.end()) // true
cout << "22 is found\n";
ust.erase(71); // delete element
if (ust.find(71) == ust.end()) // false
cout << "71 is found\n"; 可以在平均 O(1) 的時間
加入/刪除/調查元素
unordered_map
unordered_map<string, int> ump;
ump["one"] = 1;
ump["two"] = 2;
ump["three"] = 3;
//123
cout << ump["one"] << ump["two"] << ump["three"];可以在平均 O(1) 的時間
加入/刪除/調查元素
自定義雜湊
- 如果雜湊的參數已知,很容易製作使雜湊複雜度崩掉的測資 !
- 大型競程比賽常出把 預設雜湊 ,常用雜湊撞爛的測資,請盡量 "發揮點創意" 改參數 !
struct custom_hash {
size_t operator()(uint64_t x) const {
// Add a random constant
const uint64_t FIXED_RANDOM = 71222;
return x + FIXED_RANDOM;
}
};Rabin fingerprint
滾動雜湊
Rabin fingerprint
- 一般而言,雜湊常用於字串比對,以 strcmp 為例
- 單純的字串比較需要 \(O(|S_1|+|S_2|)\)
- 如果有 \(k\) 個字串要檢查,會需要 \(O(|S|\times\Sigma|S_i|)\)
如果能先將字串透過萃取成一個 int , 那只需要 \(O(1\times\Sigma{|S|})\) 的時間
Rabin fingerprint
- Rabin fingerprint 是一個很簡單的雜湊函數
- 如果字串 \(S=a_1a_2a_3a_4\dots a_n\)
- \(H(S,x)=a_1x^{n-1}+a_2x^{n-2}+a_3x^{n-3}+\dots+a_nx^0\)
- 一般而言,會取 \(H(S,x)\) 除以 \(p\) 的餘數,\(x,p\) 必須互質
Rabin fingerprint
- 如果字串 \(S=a_1a_2a_3a_4\dots a_n\)
- \(H(S,x)=a_1x^{n-1}+a_2x^{n-2}+a_3x^{n-3}+\dots+a_nx^0\)
- 如果字串 \(S'=a_1a_2a_3a_4\dots a_na_{n+1}\)
- \(H(S',x)\\=a_1x^{n}+a_2x^{n-1}+a_2x^{n-3}+\dots+a_nx^1+a_{n+1}x^0\\=xH(S,x)+a_{n+1}\)
Rabin fingerprint
#define MAXN 1000000
#define prime_mod 1073676287
/*prime_mod 必須要是質數*/
typedef long long T;
char s[MAXN+5];
T h[MAXN+5];/*hash陣列*/
T h_base[MAXN+5];/*h_base[n]=(prime^n)%prime_mod*/
inline void hash_init(int len,T prime=0xdefaced){
h_base[0]=1;
for(int i=1;i<=len;++i){
h[i]=(h[i-1]*prime+s[i-1])%prime_mod;
h_base[i]=(h_base[i-1]*prime)%prime_mod;
}
}Rabin fingerprint
Rabin fingerprint 具有滾動的性質,如果知道每一個前綴的 Hash,很容易可以推算中間任意一段的 Hash
\(S'=a_La_{L+1}a_{L+2}\dots a_R\)
求\(H(S',x)=a_Lx^{R-L}+a_{L+1}x^{R-L-1}+\dots+a_Rx^0\)
Rabin fingerprint
\(S'=a_La_{L+1}a_{L+2}\dots a_R\)
求\(H(S',x)=a_Lx^{R-L}+a_{L+1}x^{R-L-1}+\dots+a_Rx^0\)
\(S_R=a_1a_2a_3\dots a_R\)
\(H(S_R,x)=a_1x^{R-1}+a_2x^{R-2}+\dots+a_{L-1}x^{R-L+1}+a_{L}x^{R-L}+\dots+a_Rx^0\)
\(S_{L-1}=a_1a_2a_3\dots a_{L-1}\)
\(H(S_{L-1},x)=a_1x^{L-2}+a_2x^{L-3}+\dots+a_{L-1}x^{0}\)
Rabin fingerprint
\(S'=a_La_{L+1}a_{L+2}\dots a_R\)
求\(H(S',x)=a_Lx^{R-L}+a_{L+1}x^{R-L-1}+\dots+a_Rx^0\)
\(S_R=a_1a_2a_3\dots a_R\)
\(H(S_R,x)=a_1x^{R-1}+a_2x^{R-2}+\dots+a_{L-1}x^{R-L+1}+a_{L}x^{R-L}+\dots+a_Rx^0\)
\(S_{L-1}=a_1a_2a_3\dots a_{L-1}\)
\(H(S_{L-1},x)=a_1x^{L-2}+a_2x^{L-3}+\dots+a_{L-1}x^{0}\)
\(H(S',x)=H(S_R,x)-x^{R-L+1}H(S_{L-1},x)\)
inline T get_hash(int l,int r){
return (h[r+1]
-(h[l]*h_base[r-l+1])
%prime_mod+prime_mod)
%prime_mod;
}文本匹配問題
有一本書,當作是字串 S
想問一個單字 T 在這本書裡面出現幾次
文本匹配問題
KMP Algorithm \(O(|S|+|T|)\)
剛剛的那一個
文本匹配問題
Rabin–Karp Algorithm \(O(|S|+|T|)\)
唬爛法
計算 S 所有前綴的雜湊 : \(O(S)\)
計算 T 的雜湊 : \(O(T)\)
檢查 S 中所有長度為 \(|T|\) 的字串,雜湊是否與 T 相同 : \(O(S)\)
雜湊 - 唬爛法
- 很多字串問題看起來很有深度,但其實沒有好的演算法
- 或是腦袋一時卡住,想不到好方法
雜湊可以把字串比對的複雜度從 \(O(n)\) 下降到 \(O(1)\)

讓暴力演算法複雜度下降
\(O(n)\) 到 \(O(\log n)\)
看起來可以 AC

人品太差
因為雜湊碰撞導致
WA
Rabin fingerprint
若 \(H(S,x)\) 中 \(x\) 夠大,就相當於把 \(S\) 編碼程 \(x\) 進位的整數
若 \(S\) 輸入是隨機的,且 \(x,p\) 互質
那碰撞率為 \(1/p\)
換句話說只跟取的餘數有關係
如果進行 \(k\) 次比較,希望有 90 % 的正確率, \(p\) 要多大?
Rabin fingerprint
如果進行 \(k\) 次比較,希望有 90 % 的正確率, \(p\) 要多大?
\((1-1/p)^k\geq 0.9\)
\(1-1/p\geq 0.9^{1/k}\)
\(p\geq 1/(1- 0.9^{1/k})\)
int 不夠大怎麼辦? 算多個雜湊一起比較!
根據有人推的近似公式 (待補證明)
\(p\geq 5 k^2\)
練習題
- CSES - Palindrome Queries
- ZJ d518
- TIOJ 1306
- TIOJ 1321
\(p\) 請勿選擇 \(2^n-1\) 的質數,容易被構造特殊測資
最常見 : INT_MAX \(2^{31}-1\)