Reinterpretation of
the Starobinsky model
Takahiro Terada
(JSPS fellow; The University of Tokyo, DESY)
Based on arXiv:1507.04344 [hep-th] with T. Asaka, S. Iso, H. Kawai, K. Kohri, T. Noumi.
The 27th International Symposium on Lepton Photon Interactions at High Energies, Ljubljana, Slovenia, August 21, 2015
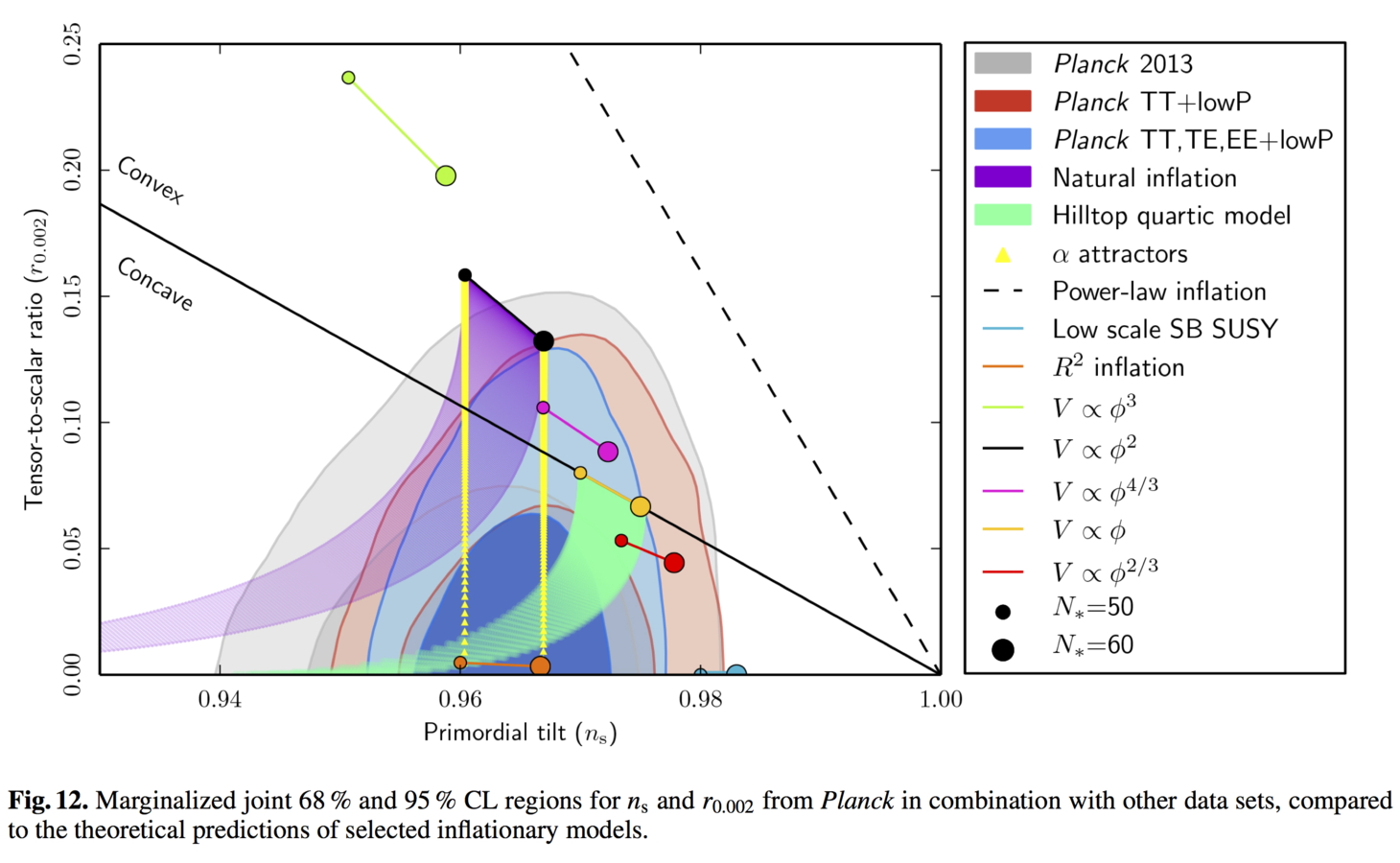
P. A. R. Ade et al. [Planck Collaboration], "Planck 2015 results. XX. Constraints on inflation", arXiv:1502.02114 [astro-ph.CO].
Peculiar Form of the Action
S= \int \text{d}^4 x \sqrt{-g} \left(-\frac{1}{2} M_{\text{P}}^2 R + \frac{M_{\text{P}}^2}{12 m^2}R^2 \right)
Approaches
1. Scale invariance
2. Extra dimensions
Higher dimensional action
S= \Lambda^{D} \int \text{d}^D x \sqrt{-g} \sum_{n=0} b_n \left( \frac{R_D}{\Lambda^{2}} \right)^n
Compactification
= c \int \text{d}^4 x \sqrt{-g} \sum_{n=0} b_n \Lambda^4 \left( \frac{R}{\Lambda^{2}} \right)^n
LARGE
c=(L \Lambda)^{D-4} \simeq 5 \times 10^8 \quad \text{for} \, \, L=30/\Lambda.
Tuning one parameter
(in addition to the cosmological constant)
L= -\frac{1}{2}M_{\text{P}}^2 R + \frac{M_{\text{P}}^2}{12m^2}\left( R^2 + \sum_{n=3}^{\infty} b_{n} \left(- \frac{6 m^2}{b_1}\right)^{2-n} R^n \right)
c b_1 \Lambda^2 =- \frac{M_{\text{P}}^2}{2}, \qquad c= \frac{M_{\text{P}}^2}{12m^2}\simeq 5 \times 10^8,
Take
then,
Take
|b_1 | \ll 1.
Modified potential
V=V_{\text{Starobinsky}}\times \left( 1-\frac{b}{2}e^{\sqrt{2/3}\phi}\left(1-e^{-\sqrt{2/3}\phi} \right) \right) + O(b^2)
V_{\text{Starobinsky}}=\frac{3}{4}m^2\left(1-e^{-\sqrt{2/3}\phi }\right)^2
where
b= b_1 b_3.
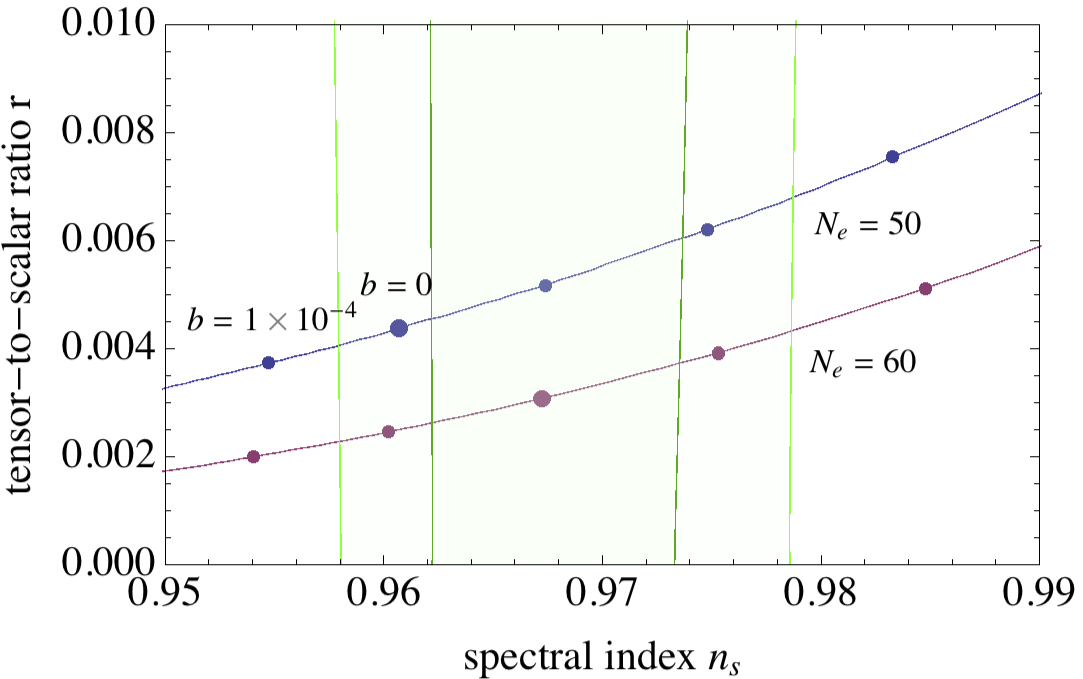
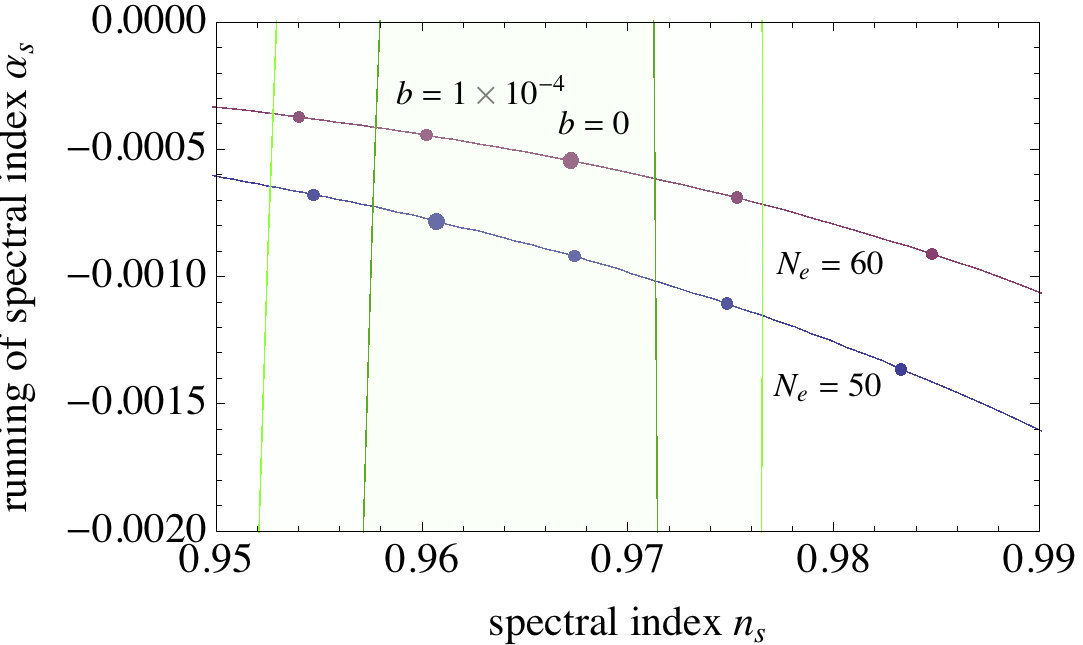
Summary
- Starobinsky model has a peculiar form of the action.
\Lambda \simeq 5 \times 10^{16} \text{GeV} \left( \frac{2\times 10^{-4}}{|b_1|} \right)^{\frac{1}{2}}.
If the deviation is observed, it implies the fundamental scale,
- It may be originated from extra dimensions.
- One tuning is needed to be consistent with data.