Dojo:

A differentiable simulator for robotics

Simon Le Cleac'h and Taylor Howell

Taylor Howell

Simon Le Cleac'h

Jan Brüdigam

Zico Kolter

Mac Schwager

Zachary Manchester

team

Dojo is a physics engine

that prioritizes

physical accuracy

and

differentiability

doesn't

MuJoCo/Drake/Bullet/Brax

already do that?

popular simulators

https://leggedrobotics.github.io/SimBenchmark/

github.com/dojo-sim

  • Julia package: Dojo.jl
  • Python wrapper: dojopy
    • gym-like environments
    • interface w/ PyTorch & JAX
  • maximal-coordinates representation
  • variational integrator
  • higher-fidelity contact model
  • custom interior-point solver
  • smooth gradients

Dojo

maximal-coordinates representation

minimal-coordinates

representation

minimal-coordinates

representation

(x,v,q,\omega) \in \mathbf{R}^{13}

minimal-coordinates

representation

(x,v,q,\omega) \in \mathbf{R}^{13}
(\theta_1, \dot{\theta}_1) \in \mathbf{R}^2

minimal-coordinates

representation

(x,v,q,\omega) \in \mathbf{R}^{13}
(\theta_1, \dot{\theta}_1) \in \mathbf{R}^2
(\theta_2, \dot{\theta}_2) \in \mathbf{R}^2

minimal-coordinates

representation

(x,v,q,\omega) \in \mathbf{R}^{13}
(\theta_1, \dot{\theta}_1) \in \mathbf{R}^2
(\theta_2, \dot{\theta}_2) \in \mathbf{R}^2
(\theta_3, \dot{\theta}_3) \in \mathbf{R}^2

minimal-coordinates

representation

(x,v,q,\omega) \in \mathbf{R}^{13}
(\theta_1, \dot{\theta}_1) \in \mathbf{R}^2
(\theta_2, \dot{\theta}_2) \in \mathbf{R}^2
(\theta_3, \dot{\theta}_3) \in \mathbf{R}^2
\mathbf{R}^{37}

maximal-coordinates

representation

maximal-coordinates

representation

(x_1,v_1,q_1,\omega_1) \in \mathbf{R}^{13}

maximal-coordinates

representation

(x_1,v_1,q_1,\omega_1) \in \mathbf{R}^{13}
(x_2,v_2,q_2,\omega_2) \in \mathbf{R}^{13}

maximal-coordinates

representation

(x_1,v_1,q_1,\omega_1) \in \mathbf{R}^{13}
(x_2,v_2,q_2,\omega_2) \in \mathbf{R}^{13}
(x_3,v_3,q_3,\omega_3) \in \mathbf{R}^{13}

maximal-coordinates

representation

(x_1,v_1,q_1,\omega_1) \in \mathbf{R}^{13}
(x_2,v_2,q_2,\omega_2) \in \mathbf{R}^{13}
(x_3,v_3,q_3,\omega_3) \in \mathbf{R}^{13}
(x_4,v_4,q_4,\omega_4) \in \mathbf{R}^{13}

maximal-coordinates

representation

(x_1,v_1,q_1,\omega_1) \in \mathbf{R}^{13}
\mathbf{R}^{169}
(x_2,v_2,q_2,\omega_2) \in \mathbf{R}^{13}
(x_3,v_3,q_3,\omega_3) \in \mathbf{R}^{13}
(x_4,v_4,q_4,\omega_4) \in \mathbf{R}^{13}

maximal-coordinates representation

Linear-Time Variational Integrators in Maximal Coordinates. J. Brudigam and Z. Manchester.
Linear-Time Contact and Friction Dynamics in Maximal Coordinates using Variational Integrators. 
J. Brudigam and Z. Manchester.

variational integrator

variational integrator

Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S = \int_{t_1}^{t_2}{\mathcal{L} dt}

variational integrator

Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S = \int_{t_1}^{t_2}{\mathcal{L} dt}

Euler-Lagrange

F = m a

variational integrator

Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S = \int_{t_1}^{t_2}{\mathcal{L} dt}

discretize

Euler-Lagrange

F = m a
p_+ = p + h (v + mg)

variational integrator

Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S = \int_{t_1}^{t_2}{\mathcal{L} dt}
S_D = h \sum_{i=1}^{N} \mathcal{L}_i

discretize

discretize

Euler-Lagrange

F = m a
p_+ = p + h (v + mg)

variational integrator

m(p_+ -2p +p_-)/h - hmg = 0
Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S = \int_{t_1}^{t_2}{\mathcal{L} dt}

discretize

discretize

Euler-Lagrange

Euler-Lagrange

F = m a
p_+ = p + h (v + mg)
S_D = h \sum_{i=1}^{N} \mathcal{L}_i

energy and momentum conservation

tennis-racket effect

astronaut

Simulation Tools for Model-Based Robotics: Comparison of Bullet, Havok, MuJoCo, ODE and PhysX. 
T. Erez, Y. Tassa, and E. Todorov.

energy and momentum conservation

variational integrator

Euler:

J\dot{\omega} + \omega \times (I \omega) = \tau

contact model

floor penetration

drift

contact model

friction

On unilateral constraints, friction and plasticity. J. J. Moreau.
\text{minimize} \quad \text{kinetic energy} \\
\text{friction forces}
\text{subject to} \\

contact model

friction

On unilateral constraints, friction and plasticity. J. J. Moreau.
\text{minimize} \quad \text{kinetic energy} \\
\text{friction forces}
\text{subject to} \\

friction cones

approximation

exact

friction cones

Subtitle

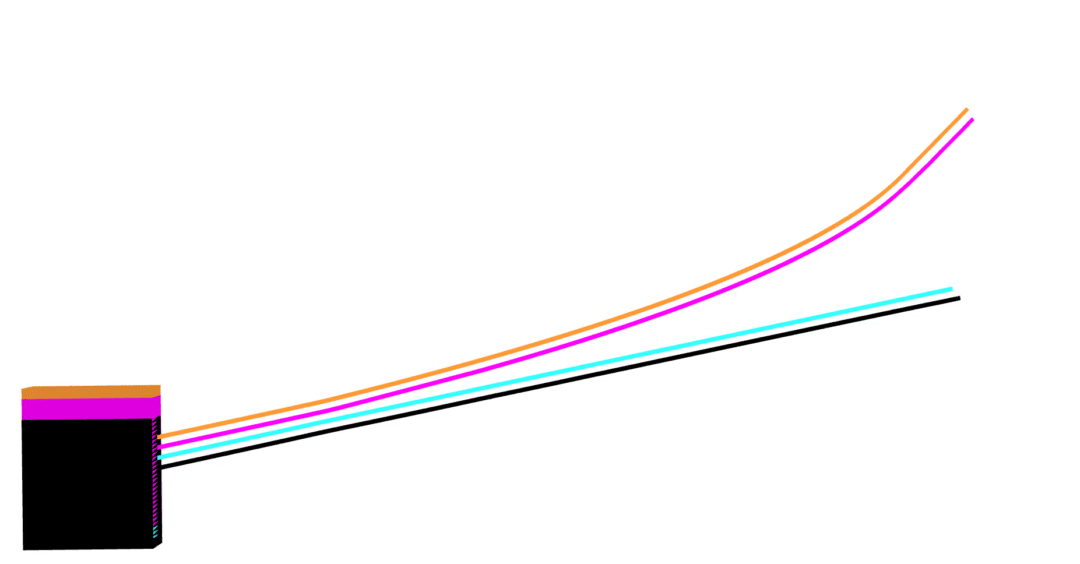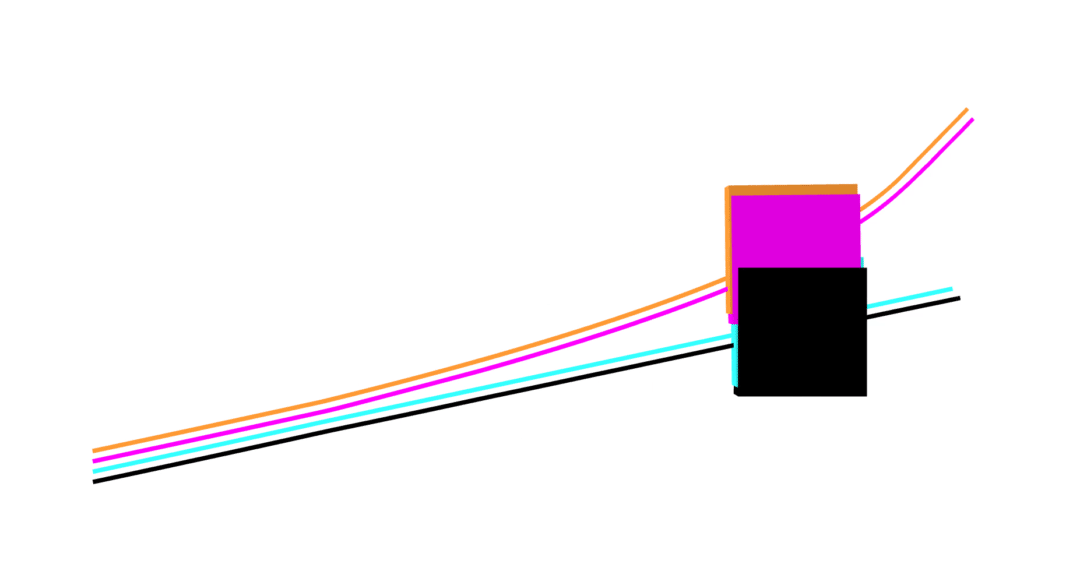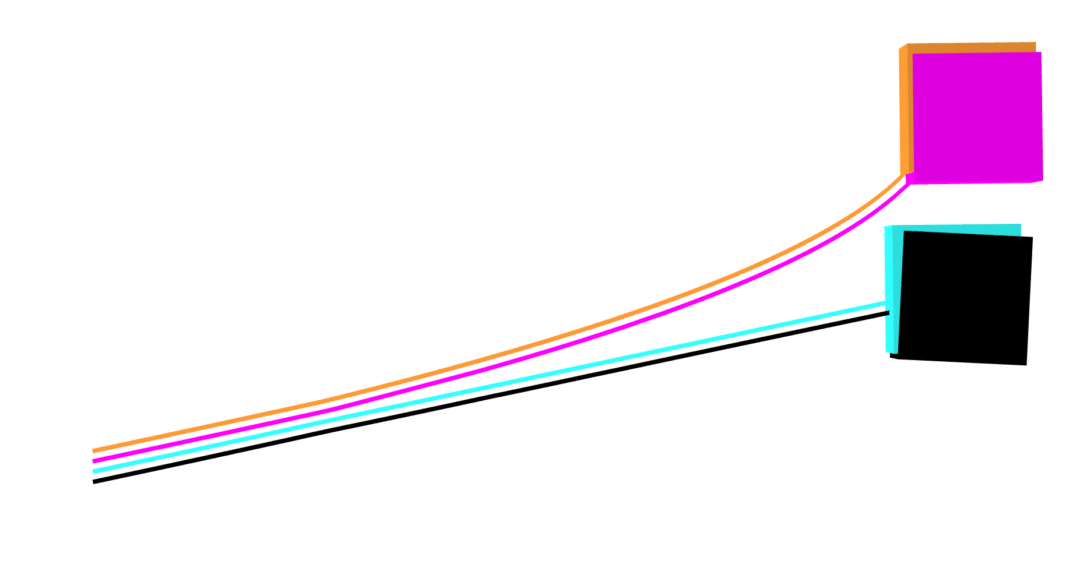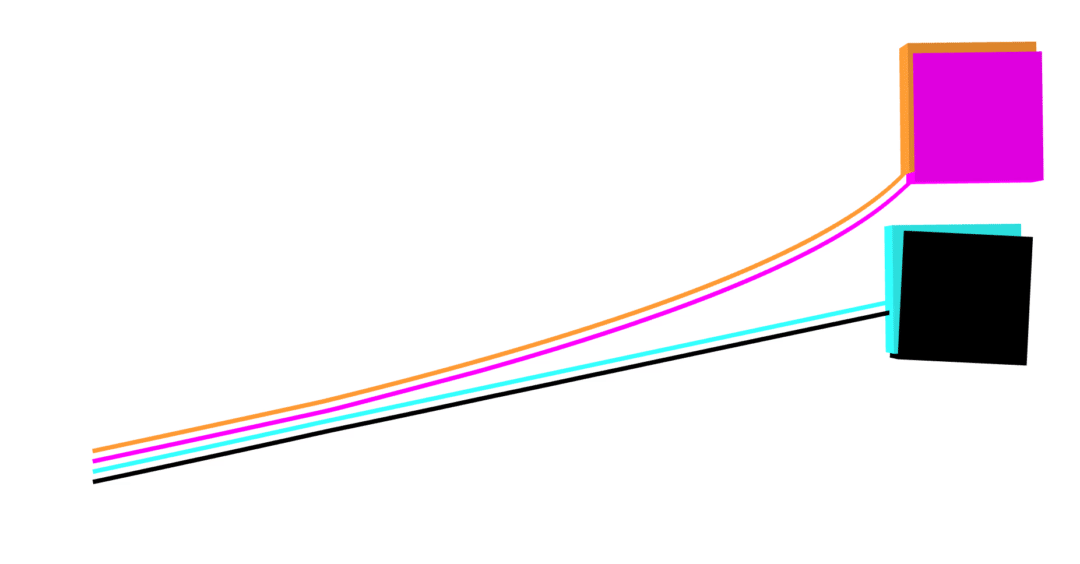
MuJoCo linear

Dojo linear

MuJoCo nonlinear

Dojo nonlinear

contact model

impact

An Implicit Time-Stepping Scheme for Rigid Body Dynamics with Inelastic Collisions and Coloumb Friction. D. E. Stewart and J. C. Trinkle.
x
p
x

contact model

impact

An Implicit Time-Stepping Scheme for Rigid Body Dynamics with Inelastic Collisions and Coloumb Friction. D. E. Stewart and J. C. Trinkle.
\phi(x) \geq 0
x
p
x

contact model

impact

An Implicit Time-Stepping Scheme for Rigid Body Dynamics with Inelastic Collisions and Coloumb Friction. D. E. Stewart and J. C. Trinkle.
\phi(x) \geq 0
x
\gamma \geq 0
p
x

contact model

impact

An Implicit Time-Stepping Scheme for Rigid Body Dynamics with Inelastic Collisions and Coloumb Friction. D. E. Stewart and J. C. Trinkle.
\phi(x) \geq 0
x
\gamma \geq 0
p
\gamma \circ \phi(x) = 0
x

impact

Dojo

MuJoCo

interior-point solver

\text{minimize} \quad f(x)
x
\text{subject to}
\phi(x) \geq 0

interior-point solver

\text{minimize} \quad f(x)
x
\text{subject to}
\phi(x) \geq 0
\text{minimize} \quad f(x) -\kappa \:\log(\phi(x))
x

interior-point solver

\text{minimize} \quad f(x)
x
\text{subject to}
\phi(x) \geq 0
\text{minimize} \quad f(x) -\kappa \:\log(\phi(x))
x
x
f(x) = x \\ \phi(x) = x

interior-point solver

\text{minimize} \quad f(x)
x
\text{subject to}
\phi(x) \geq 0
\text{minimize} \quad f(x) -\kappa \:\log(\phi(x))
x
x
f(x) = x \\ \phi(x) = x

interior-point solver

\text{minimize} \quad f(x)
x
\text{subject to}
\phi(x) \geq 0
\text{minimize} \quad f(x) -\kappa \:\log(\phi(x))
x
x
f(x) = x \\ \phi(x) = x

interior-point solver

\text{minimize} \quad f(x)
x
\text{subject to}
\phi(x) \geq 0
\text{minimize} \quad f(x) -\kappa \:\log(\phi(x))
x
x
x
f(x) -\kappa \:\log(\phi(x))
f(x) = x \\ \phi(x) = x

interior-point solver

\text{minimize} \quad f(x)
x
\text{subject to}
\phi(x) \geq 0
\kappa \rightarrow 0
\text{minimize} \quad f(x) -\kappa \:\log(\phi(x))
x
x
x
f(x) -\kappa \:\log(\phi(x))
f(x) = x \\ \phi(x) = x

interior-point solver

KKT conditions

\nabla f(x) + \nabla \phi(x)^T \gamma = 0 \\
\gamma \cdot \phi(x) = \kappa\\
\phi(x), \gamma \geq 0
\text{find} \quad x, \gamma
\text{subject to}
\phi
\gamma
p
\phi
\gamma
\gamma \cdot \phi(x) = \kappa

interior-point solver

KKT conditions

\nabla f(x) + \nabla \phi(x)^T \gamma = 0 \\
\gamma \cdot \phi(x) = \kappa \\
\phi(x), \gamma \ge 0
\text{find} \quad x, \gamma
\text{subject to}
\phi
\gamma
p
\phi
\gamma
\gamma \cdot \phi(x) = \kappa
0 \leftarrow \kappa

interior-point solver

\geq 0

interior-point solver

\geq 0

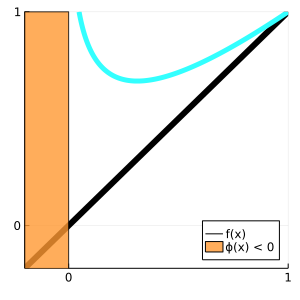
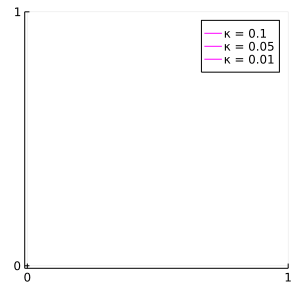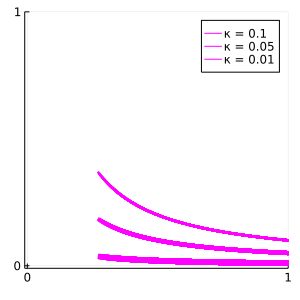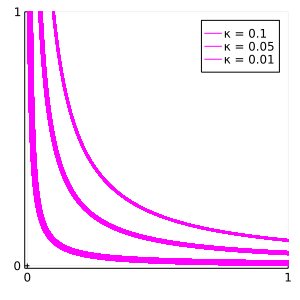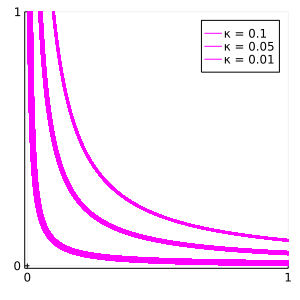
interior-point solver

using Plots
using Dojo

rectangle(w, h, x, y) = Shape(x .+ [0,w,w,0], y .+ [0,0,h,h])
light_blue = RGBA(0.4,0.4,1.0,0.8)

f(x) = x
ϕ(x) = x
L(x, ρ) = f(x) - ρ * log.(ϕ(x))
X = 0:0.0001:1
Y = -1:0.1:1
plt = plot(ylims=(-0.2,1.0), xlims=(-0.2,1.0), yticks=[0,1], xticks=[0,1], legend=:bottomright, size=(300,300))
plot!(plt, Y, f.(Y), linewidth=6.0, color=:black, label="f(x)")
plot!(rectangle(-0.2,2,0,-1), opacity=.6, color=:red, label="ϕ(x) < 0")
anim = @animate for i = 1:10
    plot!(plt, X, [1; L.(X[2:end], 10*0.5^i)], linewidth=5.0, color=light_blue, label=false)# label="ρ = 3e-1")
end
gif(anim, fps=10, "/home/simon/Downloads/anim.gif")

PHI = Vector(1:-0.005:0)
plt = plot(ylims=(-0.01,1.0), xlims=(-0.01,1.0), yticks=[0,1], xticks=[0,1], legend=:topright, size=(300,300), )
anim = @animate for i = 1:440
    # for (j,κ) ∈ enumerate([1e-1, 5e-2, 1e-2])
    for (j,κ) ∈ enumerate([5e-2,])
        PHI_i = PHI[1:min(i,length(PHI))]
        (i == 1) && plot!(plt, PHI_i, κ ./ PHI_i, color=light_blue, linewidth=1+1.5j, label="κ = $κ")
        plot!(plt, PHI_i, κ ./ PHI_i, color=light_blue, linewidth=1+1.5j, label=nothing)
    end
end

gif(anim, fps=40, "/home/simon/Downloads/force_solo.gif")

plot!(plt, PHI, 1e-2 ./ PHI, color=light_blue, linewidth=5.0, label="κ = 1e-2")
plot!(plt, PHI, 1e-3 ./ PHI, color=light_blue, linewidth=5.0, label="κ = 1e-3")

gradients

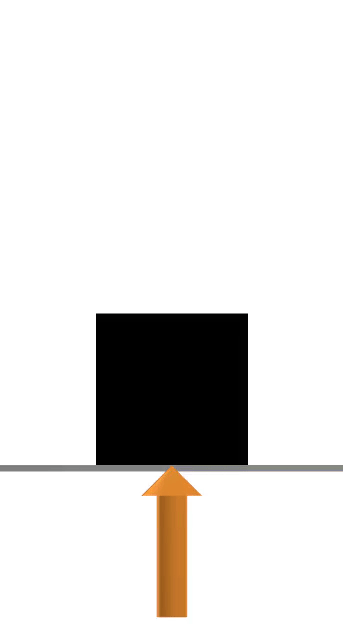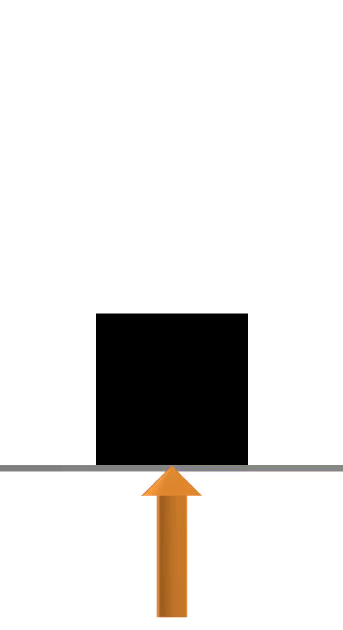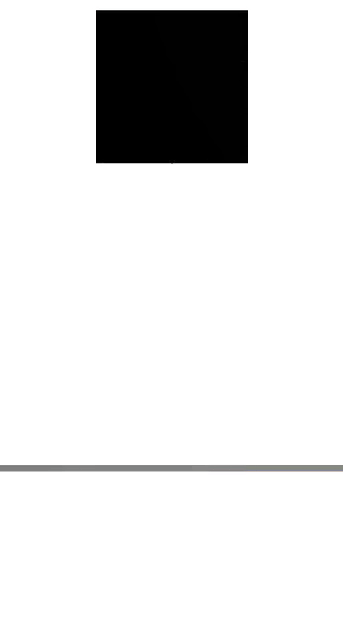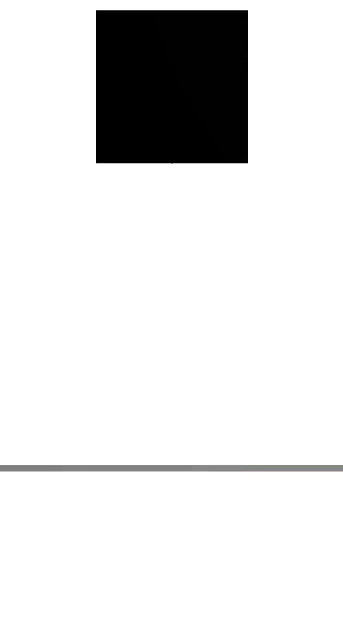
gradients

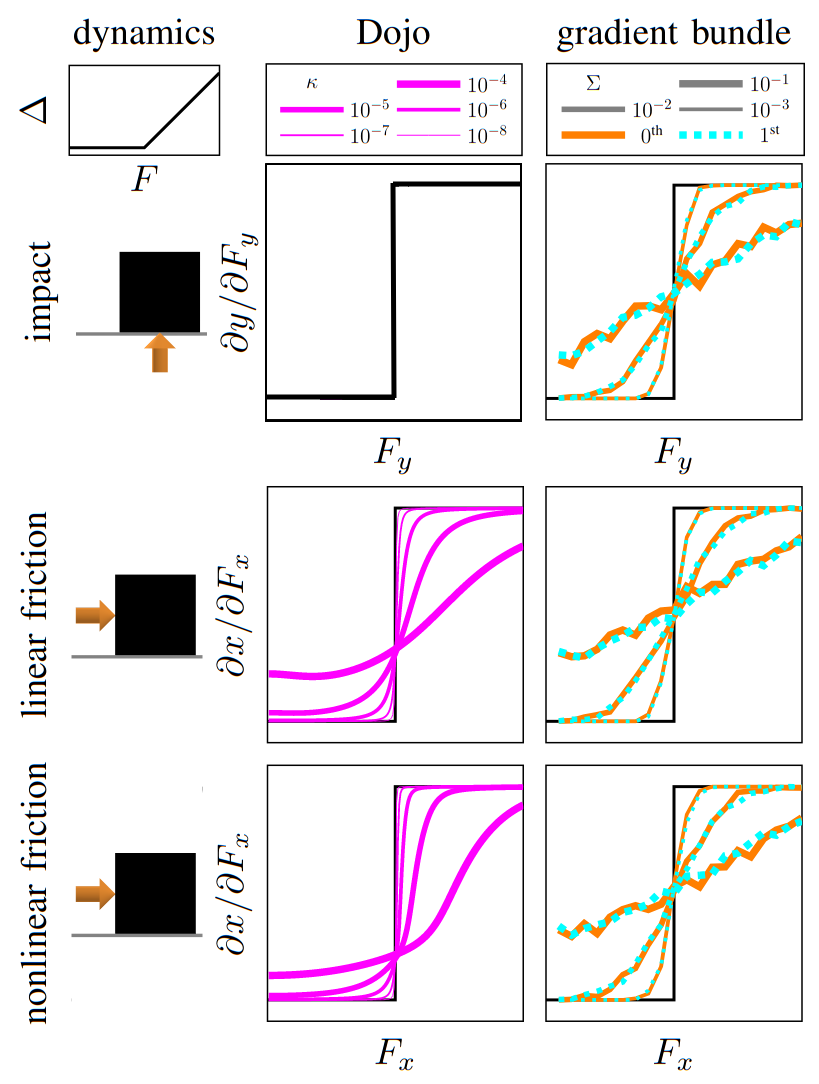
gradients

gradients

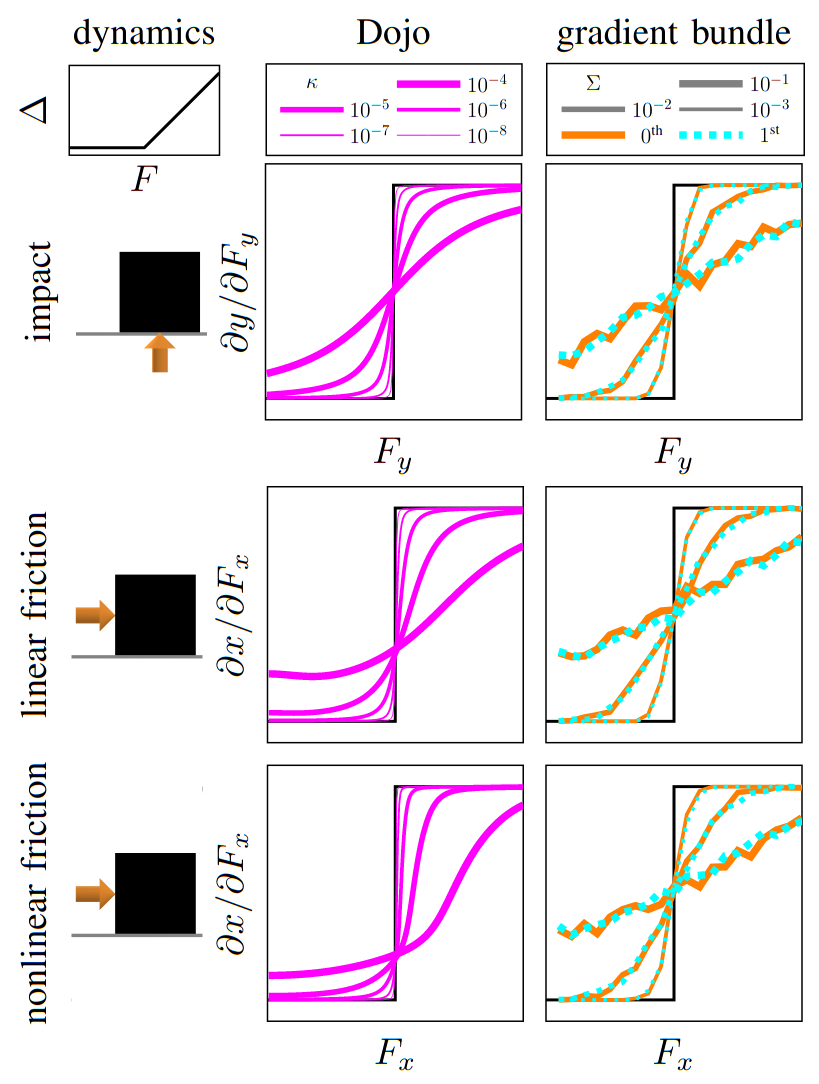
gradients

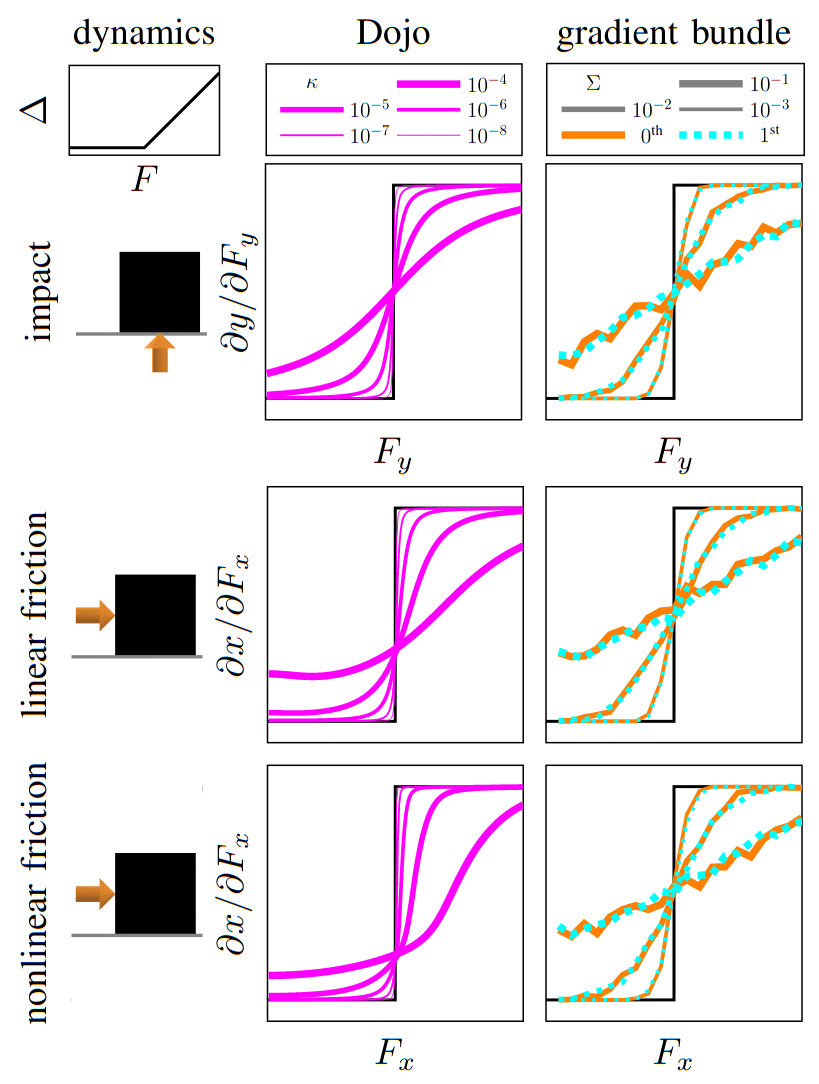
gradients

implicit-function theorem

Lezioni di analisi infinitesimale. U. Dini.
r(w^*; \theta) = 0

gradients

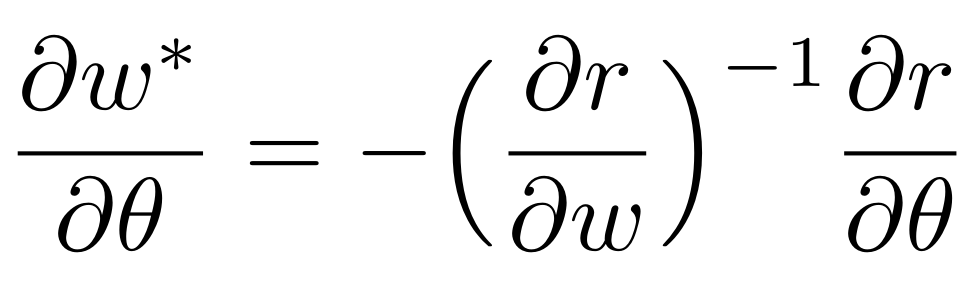
implicit-function theorem

Lezioni di analisi infinitesimale. U. Dini.

gradients

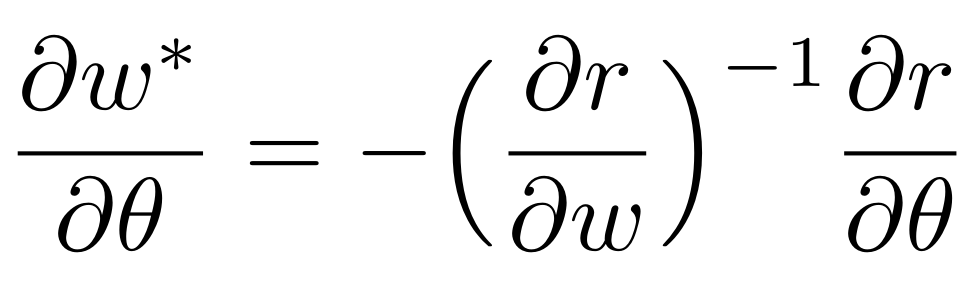
implicit-function theorem

Lezioni di analisi infinitesimale. U. Dini.

solution

gradients

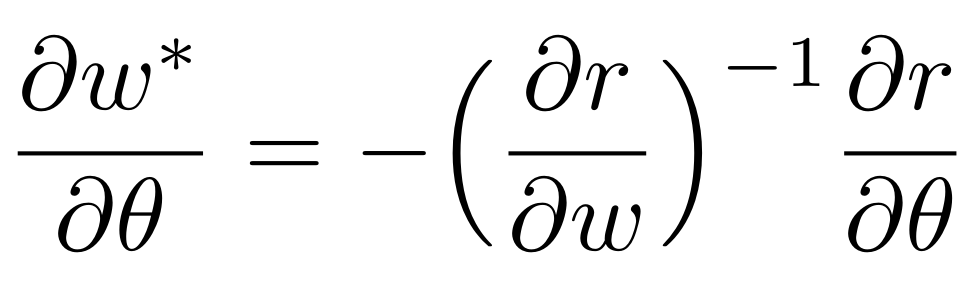
implicit-function theorem

Lezioni di analisi infinitesimale. U. Dini.

solution

residual

gradients

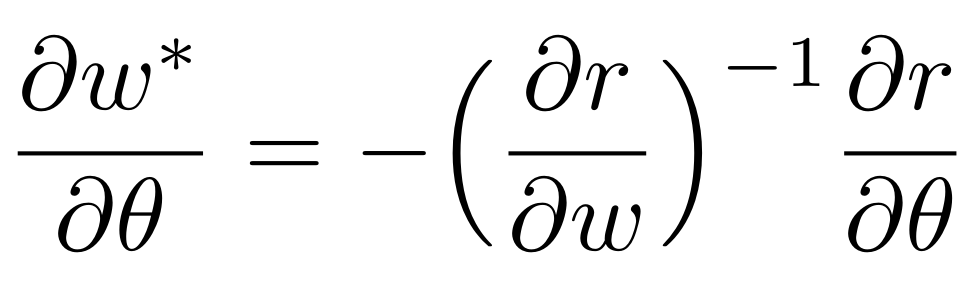
implicit-function theorem

Lezioni di analisi infinitesimale. U. Dini.

solution

data

residual

trajectory optimization

Dojo: success

MuJoCo: success

Dojo: success

MuJoCo: failure

gradients

\alpha = \frac{\text{dynamics evaluation time}}{\text{gradient evaluation time}}

examples

trajectory optimization

optimized with iterative LQR

reinforcement learning

Subtitle

augmented random search to train static linear policies

reinforcement learning

augmented random search v. augmented gradient search

system identification

ContactNets: Learning Discontinuous Contact Dynamics with Smooth, Implicit Representations. 
S. Pfrommer, M. Halm, and M. Posa.

system identification

ContactNets: Learning Discontinuous Contact Dynamics with Smooth, Implicit Representations. 
S. Pfrommer, M. Halm, and M. Posa.

learned

 

ground-truth

system identification

learning via quasi-Newton method

geometry

friction coefficient

 

ground-truth

learned

system identification

system identification

Dojo gradient

live demo

model-predictive control

model-predictive control

model-predictive control

model-predictive control

NeRF

fast policy learning

github.com/dojo-sim

Made with Slides.com