But first, some linear algebra:

Basis vectors are a set of vectors able to represent another vector in the same space as a linear combination of basis vectors

Or, more simply:

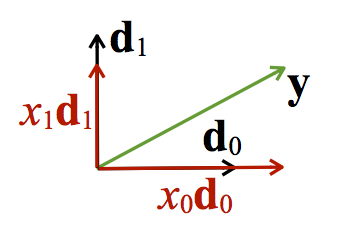
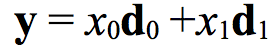
Or even more simply, as an example,

(1, 3) = (1, 0) + (0, 3)

A linear combination is a weighted sum of vectors

A set of basis vectors doesn't necessarily need to be unit length (i.e. (1, 0) and (0, 1)) or perpendicular

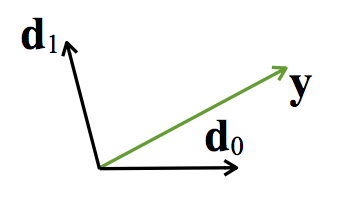
(If they are, that's called an orthonormal basis)

Signals and Sampling

Theoretical sample from something, anything: audio, color, position, rotation, etc.

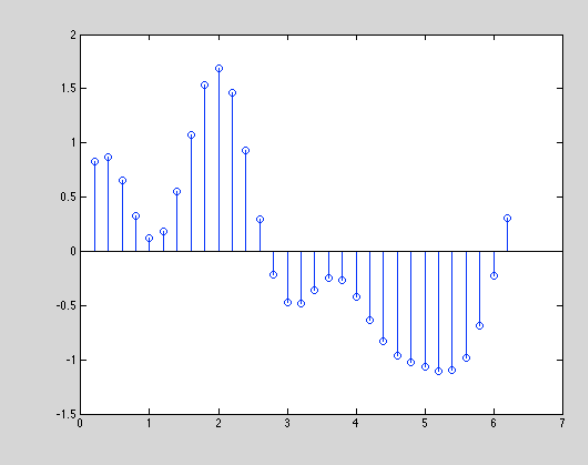
Terminology:

• Dictionary: set of signals used to represent sample
  • Could be basis vectors, as described earlier
• Atom: Element of dictionary

Example representation of earlier signal using Real Fourier series as dictionary:

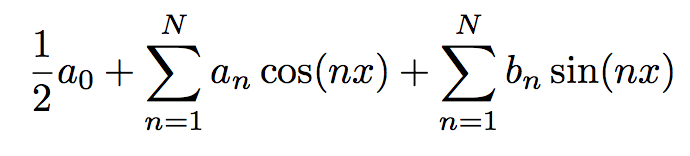
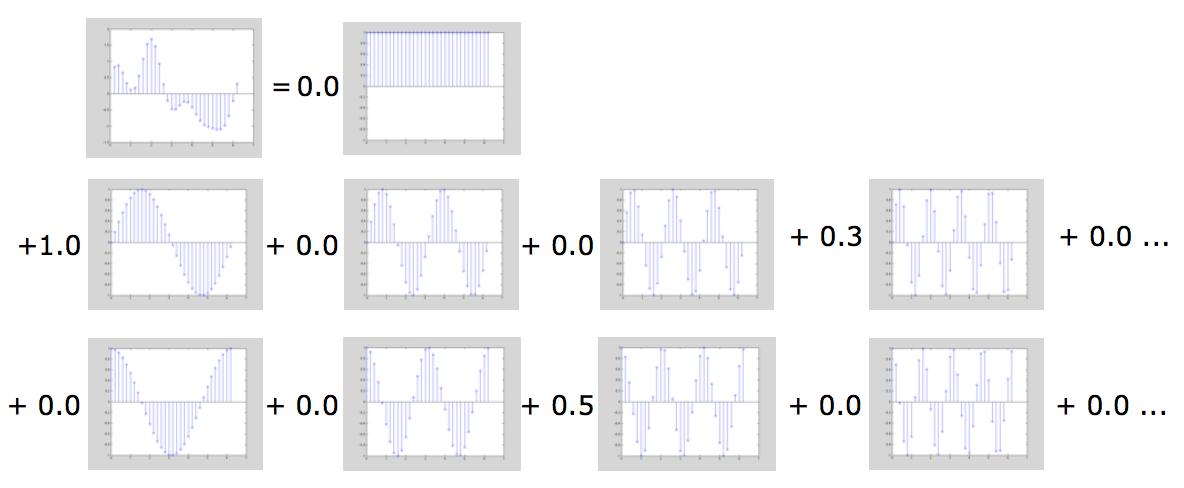
Choosing a Dictionary

• Usually the issue is finding the right dictionary to compress certain kinds of data
• Fourier Series can introduce discontinuities, for ex.
• Most dictionaries are orthonormal bases, where you need all coefficients
  • (All those 0s in Fourier example...)

Making a Dictionary

• Bottom-up approach:
  • Make dictionary based on signal
• Get best of both worlds:
  • sparsity of data size
  • accurate representation (minimal discontinuities)

Matching Pursuit

• Better than least squares (slow)
• Uses frames
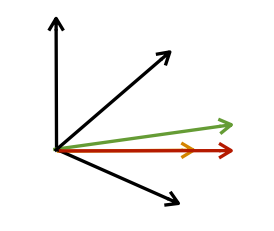
  • Frames are an overspecified basis
    • More basis vectors (nonredundant)
    • But still needs to span

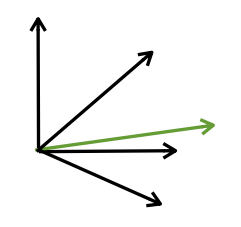
Black: vectors in dictionary

Green: sample we intend to compress

Matching Pursuit, cont.

• Iterate over dictionary
  • Project sample onto all dictionary entries
    • Find dictionary entry with largest projected magnitude

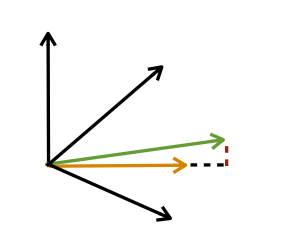
• Add it to set
• Store as pair
  • Coefficient and vector
  • e.g. 1.3, (1, 0) 

• Subtract atom from sample to get residual

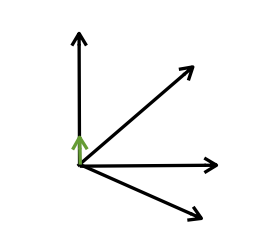
1.3, (0, 1)

0.2, (1, 0)

Even more can be done!

• Can oscillate between atoms - ways around this
• Can use method called K-SVD to even better tailor dictionary to input data

To Be Continued!