Algorithms complexity
Telerik Academy Alpha

 

DSA

 Table of contents

Algorithm complexity

 Algorithm analysis

  • Why we should analyze algorithms?
    • Predict the resources the algorithm requires
      • Computational time (CPU consumption)
      • Memory space (RAM consumption)
      • Communication bandwidth consumption
    • The running time of an algorithm is:
      • The total number of primitive operations executed (machine independent steps)
      • Also known as algorithm complexity

 

 Algorithmic complexity

  • What to measure?
    • CPU Time
    • Memory
    • Number of steps
    • Number of particular operations
      • Number of disk operations
      • Number of network packets
    • Asymptotic complexity

 

 Time Complexity

  • Worst-case
    • An upper bound on the running time for any input of given size
  • Average-case
    • Assume all inputs of a given size are equally likely
  • Best-case
    • The lower bound on the running time (the optimal case)

 Time Complexity - example

  • Sequential search in a list of size n
    • Worst-case:
      • n comparisons
    • Best-case:
      • 1 comparison
    • Average-case:
      • n/2 comparisons
  • The algorithm runs in linear time
    • Linear number of operations

 Algorithms Complexity

  • Algorithm complexity is a rough estimation of the number of steps performed by given computation depending on the size of the input data
    • Measured through asymptotic notation
      • O(g) where g is a function of the input data size
    • Examples:
      • Linear complexity O(n) – all elements are processed once (or constant number of times)
      • Quadratic complexity O(n^2) – each of the elements is processed n times

 Asymptotic Notation

  • Asymptotic upper bound
    • O-notation (Big O notation)
  • For given function g(n), we denote by O(g(n)) the set of functions that are different than g(n) by a constant
    ​

\( O(g(n)) \) = {\( f(n) \): there exist positive constants \( c \) and \( n_0 \) such that \( f(n) \leq c*g(n) \) for all \( n \geq n_0 \) } 

3*n^2 + n/2 + 12 \in O(n^2)
3∗n2+n/2+12∈O(n2)3*n^2 + n/2 + 12 \in O(n^2)
3*n*log_2(3*n+1)+2*n-1 \in O(n*log n)
3∗n∗log2(3∗n+1)+2∗n−1∈O(n∗logn)3*n*log_2(3*n+1)+2*n-1 \in O(n*log n)

 Typical Complexities

Complexity Notation Description
constant O(1) Constant number of operations, not depending on the input data size, e.g. n = 1 000 000 → 1-2 operations
logarithmic O(log n) Number of operations proportional of log2(n) where n is the size of the input data, e.g. n = 1 000 000 000 → 30 operations
linear O(n) Number of operations proportional to the input data size,
e.g. n = 10 000 → 5 000 operations
quadratic O(n^2) Number of operations proportional to the square of the size of the input data, e.g. n = 500→ 250 000 operations
cubic O(n^3) Number of operations proportional to the cube of the size of the input data, e.g. n = 200 → 8 000 000 operations
exponential O(2^n)
O(k^n)
O(n!)		 Exponential number of operations, fast growing,
e.g. n = 20 → 1 048 576 operations

 Time Complexity and Speed

Complexity 10 20 50 100 1000 10000 100000
O(1) < 1s < 1s < 1s < 1s < 1s < 1s < 1s
O(log n) < 1s < 1s < 1s < 1s < 1s < 1s < 1s
O(n) < 1s < 1s < 1s < 1s < 1s < 1s < 1s
O(n*logn) < 1s < 1s < 1s < 1s < 1s < 1s < 1s
O(n^2) < 1s < 1s < 1s < 1s < 1s 2s 3-4 min
O(n^3) < 1s < 1s < 1s < 1s 20 s 5 hours 231 days
O(2^n) < 1s < 1s 26 days hangs hangs hangs hangs
O(n!) < 1s hangs hangs hangs hangs hangs hangs
O(n^n) hangs hangs hangs hangs hangs hangs hangs

 Time and Memory Complexity

  • Complexity can be expressed as formula on multiple variables, e.g.
    • Algorithm filling a matrix of size [n x m] with the natural numbers 1, 2, … will run in O(n*m)
    • A traversal of graph with n vertices and m edges will run in O(n+m)
  • Memory consumption should also be considered, for example:
    • Running time O(n) & memory requirement O(n^2)
    • n = 50 000 → OutOfMemoryException

 The Hidden Constant

  • Sometimes a linear algorithm could be slower than quadratic algorithm
    • The hidden constant could be significant
  • Example:
    • Algorithm A makes: 100*n steps → O(n)
    • Algorithm B makes: n*n/2 steps → O(n2)
    • For n < 200 the algorithm B is faster
  • Real-world example:
    • Insertion sort is faster than quicksort for n <= 16

 Polynomial Algorithms

  • A polynomial-time algorithm is one whose worst-case time complexity is bounded above by a polynomial function of its input size \( W(n) \in O(p(n)) \)
  • Examples:
    • Polynomial-time:
      • \( log(n) \)
      • \( n^2 \)
      • \( 3n^3+ 4n \)
      • \( 2 * n*log(n) \)
    • Non polynomial-time: \( 2^n, 3^n, k^n, n! \)
    • Non-polynomial algorithms hang for large input data sets

 Computational Classes

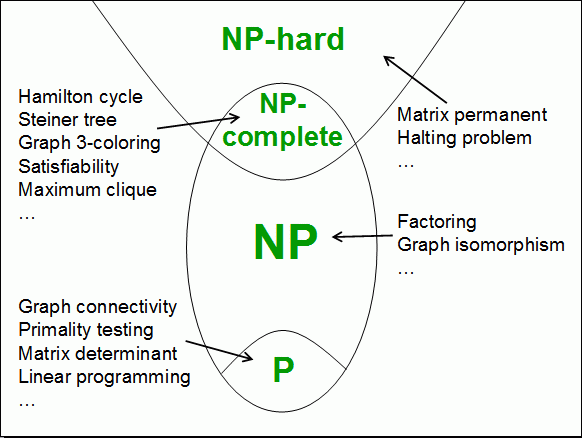
Complexity examples

 Examples

  • Runs in O(n) where n is the size of the array
    The number of elementary steps is ~n

 

int FindMaxElement(int[] array)
{
    int max = array[0];
    for (int i = 0; i < array.Length; i++)
    {
        if (array[i] > max)
        {
            max = array[i];
        }
    }
    return max;
}

 Examples

  • Runs in \( O(n^2) \) where n is the size of the array
    The number of elementary steps is ~n*(n-1)/2

 

long FindInversions(int[] array)
{
    long inversions = 0;
    for (int i = 0; i < array.Length; i++)
        for (int j = i + 1; j < array.Length; i++)
            if (array[i] > array[j])
                inversions++;
    return inversions;
}

 Examples

  • Runs in cubic time \( O(n^3) \) 
    The number of elementary steps is ~\( n^3 \)

 

decimal Sum3(int n)
{
    decimal sum = 0;
    for (int a = 0; a < n; a++)
        for (int b = 0; b < n; b++)
            for (int c = 0; c < n; c++)
                sum += a * b * c;
    return sum;
}

 Examples

  • Runs in quadratic time \( O(n*m) \)
    The number of elementary steps is ~\( n*m \)

 

long SumMN(int n, int m)
{
    long sum = 0;
    for (int x = 0; x < n; x++)
        for (int y = 0; y < m; y++)
            sum += x * y;
    return sum;
}

 Examples

  • Runs in quadratic time \( O(n*m) \)
    The number of elementary steps is ~\( n*m + min(m,n)*n \)

 

long SumMN(int n, int m)
{
    long sum = 0;
    for (int x  = 0; x < n; x++)
        for (int y = 0; y < m; y++)
            if (x == y)
                for (int i = 0; i < n; i++)
                    sum += i * x * y;
    return sum;
}

 Examples

  • Runs in exponential time \( O(2^n) \)
    The number of elementary steps is ~\(2^n \)

 

decimal Calculation(int n)
{
    decimal result = 0;
    for (int i = 0; i < (1 << n); i++)
        result += i;
    return result;
}

 Examples

  • Runs in linear time \( O(n) \)
    The number of elementary steps is ~\(n \)

 

decimal Factorial(int n)
{
    if (n == 0)
        return 1;
    else
        return n * Factorial(n-1);
}

 Examples

  • Runs in exponential time \( O(2^n) \)
    The number of elementary steps is ~\( Fib(n+1) \) where ~\( Fib(k) \) is the `k`-th Fibonacci's number

 

decimal Fibonacci(int n)
{
    if (n == 0)
        return 1;
    else if (n == 1)
        return 1;
    else
        return Fibonacci(n-1) + Fibonacci(n-2);
}

Questions?

Made with Slides.com