Graph Algorithms
Telerik Academy Alpha
DSA
Table of contents
Graphs Traversal
Algorithms
Graph Traversal Algorithms
-
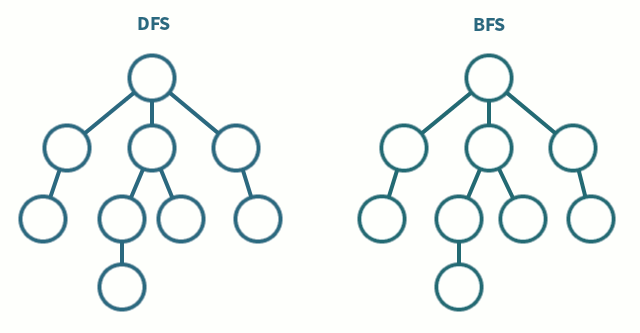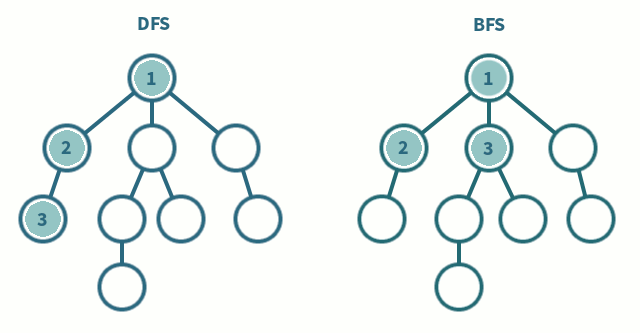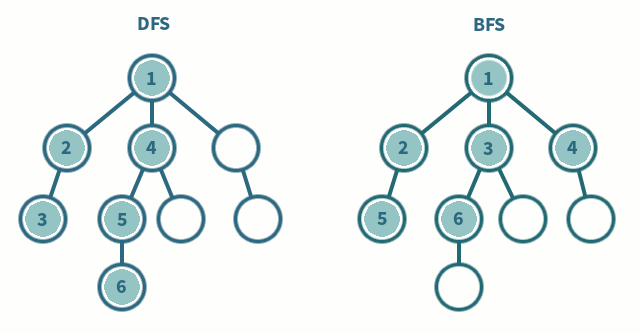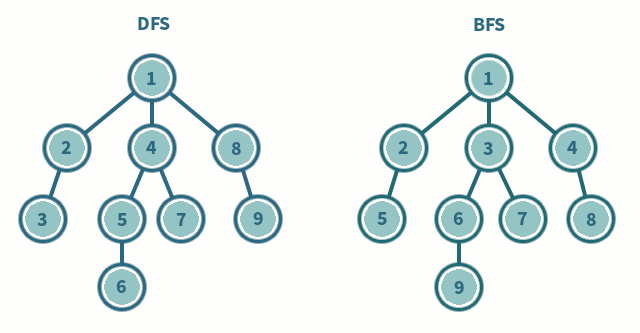
Depth-First Search (DFS) and Breadth-First Search (BFS) can traverse graphs
- Each vertex should be visited at most once
BFS(node)
{
queue ← node
visited[node] = true
while queue not empty
v ← queue
print v
for each child c of v
if not visited[c]
queue ← c
visited[c] = true
}DFS(node)
{
stack ← node
visited[node] = true
while stack not empty
v ← stack
print v
for each child c of v
if not visited[c]
stack ← c
visited[c] = true
}
Recursive DFS Graph Traversal
void TraverseDFSRecursive(node)
{
if (not visited[node])
{
visited[node] = true;
print node;
foreach child node c of node
{
TraverseDFSRecursive(c);
}
}
}
void Main()
{
TraverseDFS(firstNode);
}
Connectivity
Connectivity
-
Connected component of undirected graph
- A sub-graph in which any two nodes are connected to each other by paths

Connectivity
- A simple way to find number of connected components
- A loop through all nodes and start a DFS or BFS traversing from any unvisited node
- Each time you start a new traversing
- You find a new connected component!
- You find a new connected component!
foreach node from graph G
{
if node is unvisited
{
DFS(node);
countOfComponents++;
}
}Connectivity
-
Connected graph
- A graph with only one connected component
- Checking whether a graph is connected
- If DFS / BFS passes through all vertices → graph is connected!

Topological Sorting
Topological sorting
-
Topological sorting is just sorting a directed graph that has no cycles.
-
So you move through the nodes of the graph till you get to the end
-
Then on your way back from the recursion, you push them into the stack.
-
Because of the way the stack orders things (reverses the order), you’ll always get the first node, then the second, and so on all the way to the last
-
Topological sorting
-
Topological sorting of a directed graph
- Linear ordering of its vertices
- For every directed edge (U, V), U comes before V in the ordering
- Example:
- 7, 5, 3, 11, 8, 2, 9, 10
- 3, 5, 7, 8, 11, 2, 9, 10
- 5, 7, 3, 8, 11, 10, 9, 2

Topological sorting rules
- Sorting is not unique
- Undirected graph cannot be sorted
- Directed graphs with cycles cannot be sorted
- Various sorting algorithms exists and they give different results

Topological sorting
- Source removal algorithm
- Create an Empty List
- Find a Node without incoming Edges
- Add this Node to the end of the List
- Remove the Edge from the Graph
- Repeat until the Graph is empty
Topological sorting
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
remove a node n from S
insert n into L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least one cycle)
else
return L (a topologically sorted order)Dijkstra's Algorithm
Dijkstra's Algorithm
-
We maintain two sets, one set contains vertices included in shortest path tree, other set includes vertices not yet included in shortest path tree. At every step of the algorithm, we find a vertex which is in the other set (set of not yet included) and has minimum distance from source.
- Complexity
- \( O((|V| + |E|).log(|V|)) \)
- Complexity
- Applications – GPS, Networks, Air travels, etc.
Dijkstra's Algorithm
- Find the shortest path from vertex A to all other vertices
- The path is a directed path between them such that no other path has a lower weight.
- Assumptions
- Edges can be directed or not
- Weight does not have to be distance
- Weights are positive or zero
- Shortest path is not necessary unique
- Not all edges need to be reachable

Dijkstra's Algorithm
- In non-weighted graphs or edges with same weight finding shortest path can be done with BFS

- Note: Path from A to B does not matter - triangle inequiality
Dijkstra's Algorithm
- In weighted graphs – simple solution can be done with breaking the edges in sub-vertexes
- Note: Too much memory usage even for smaller graphs!

Dijkstra's Algorithm
-
Solution to this problem:
- Priority queue instead of queue
- Keeping information about the shortest distance so far
- Steps:
- Enqueue all distances from S
- Get the lowest in priority - B
- If edge (B, A) exists, check (S, B) + (B, A) and save the lower one
- Overcome the triangle inequality miss
Dijkstra's Algorithm
- Set the distance to every node to Infinity except the Source
- Mark every node as unprocessed
- Choose the first unprocessed node with smallest non-infinity distance as current. If there is none, the algorithm has finished
- At first we set the current node our Source
- Calculate the distance for all unprocessed neighbors by adding the current distance to the already calculated one
- Set a new value if the new distance is smaller
- Mark the current node as processed
- Repeat step 3.
Dijkstra's Algorithm
set all nodes DIST = INFINITY;
set current node the source and distance = 0;
Q -> all nodes from graph, ordered by distance;
while (Q is not empty)
a = dequeue the smallest element (first in PriorityQueue);
if (distance of a == INFINITY) break
foreach neighbour v of a
potDistance = distance of a + distance of (a-v)
if (potDistance < distance of v)
distance of v = potDistance;
reorder Q;