Binary Search Trees
Objectives:
- Define Binary Search Trees (BST)
- Describe Binary Search Algorithm
- Explain an in-order traversal of a BST
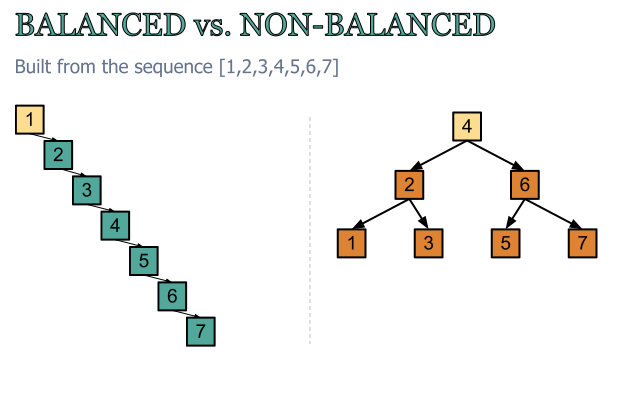
- Describe an unbalanced BST
- Describe how to balance a BST
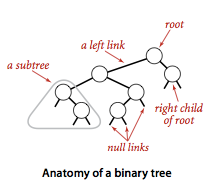
Binary Search Tree:
A binary search tree (BST) is a binary tree where each node has a Comparable key (and an associated value) and satisfies the restriction that the key in any node is larger than the keys in all nodes in that node's left subtree and smaller than the keys in all nodes in that node's right subtree
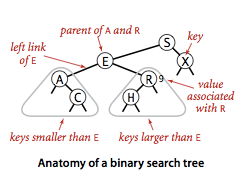
Binary Search Tree:
A binary search tree (BST) is a binary tree where...
smaller nodes go on the left and larger nodes go on the right.
Question:
What is the maximum number of links a node in a BST can have?
Answer
What is the maximum number of links a node in a BST can have?
2
It has at maximum a left and right node NOT an indefinite number of children
Why use a BST?


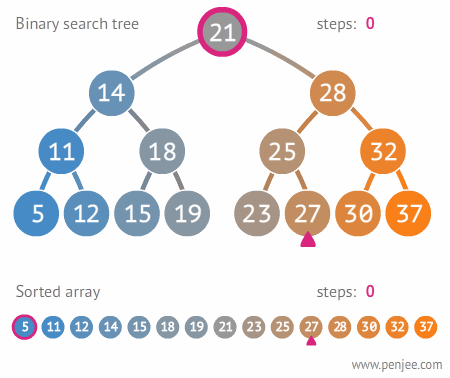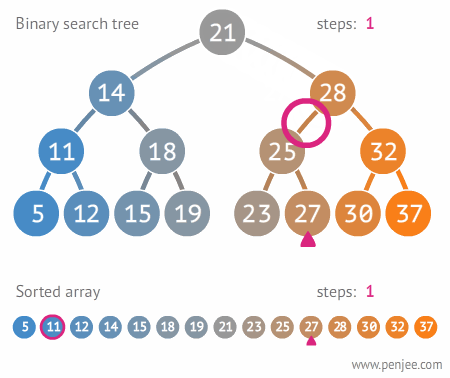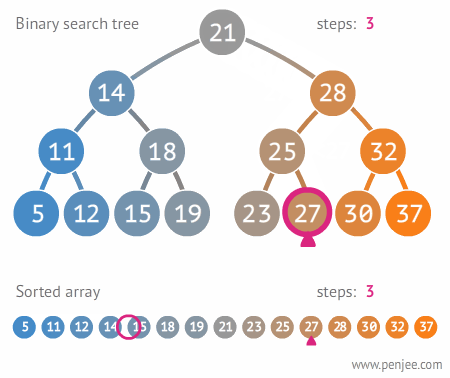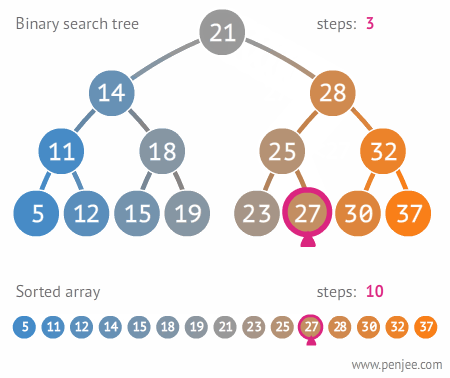
Remember...
Each comparison allows the operations to skip about half of the tree
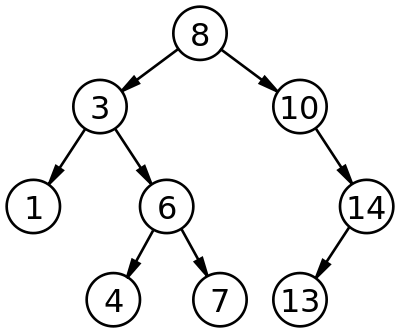
Question
What is the big O to Search, Insert, or Delete in a BST?

Answer
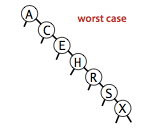
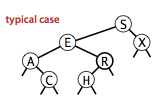
Worst case is O(n)
Typical case is closer to O(log n)
Search...
- Check to see if current node is searched node
- If not, if value is bigger go right
- If not, if value is smaller go left
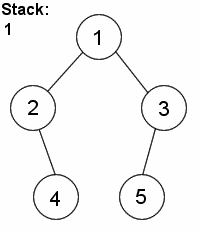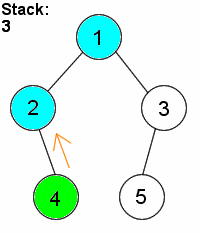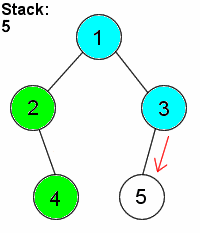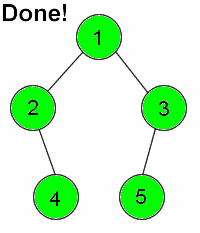
Insert...
- Check to see if current node is bigger or smaller than pushed value, move down the tree accordingly
- Continue the same process until there is no node in the next position
- Insert node at that new position
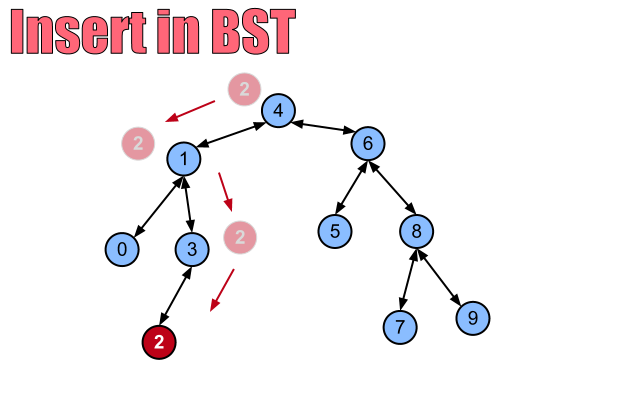
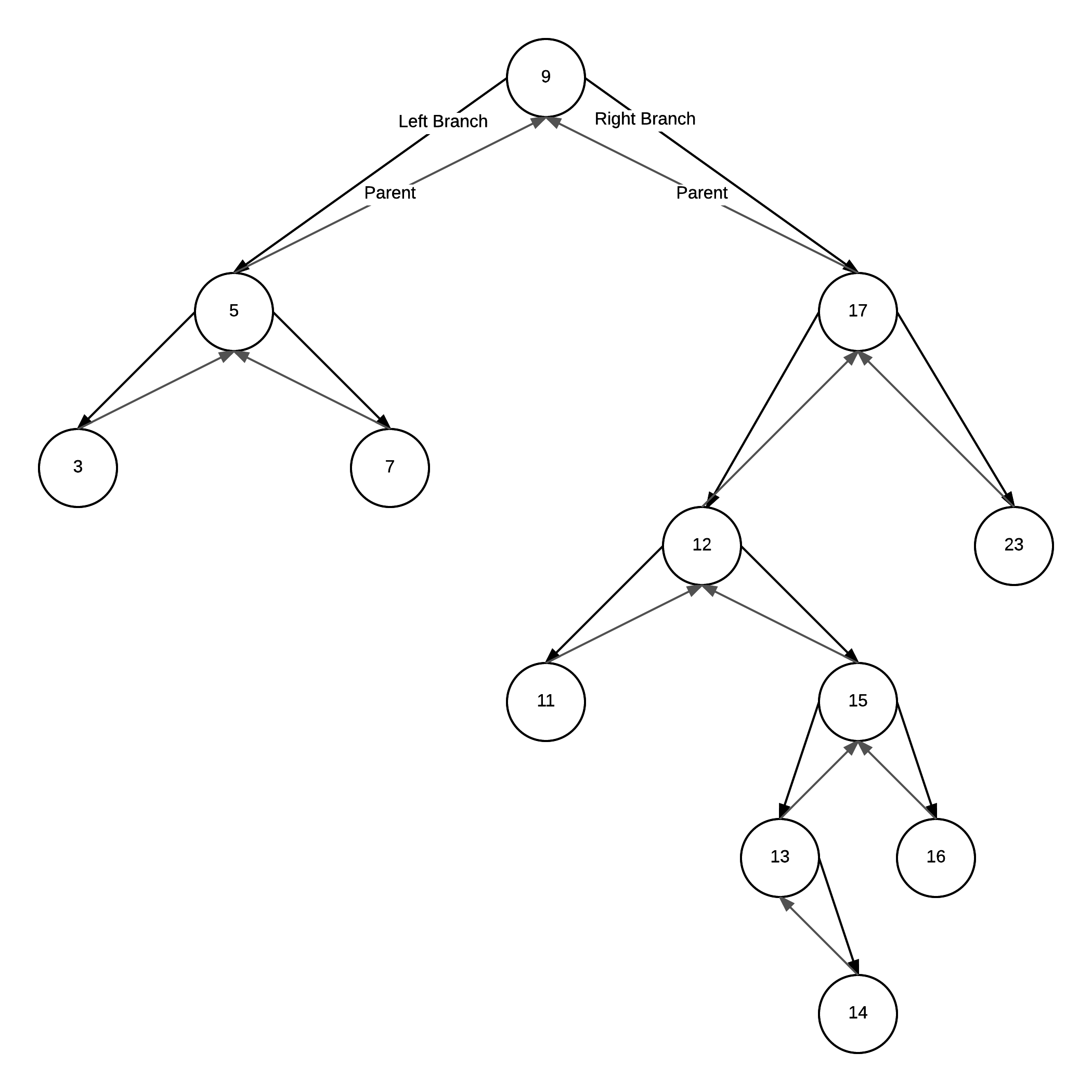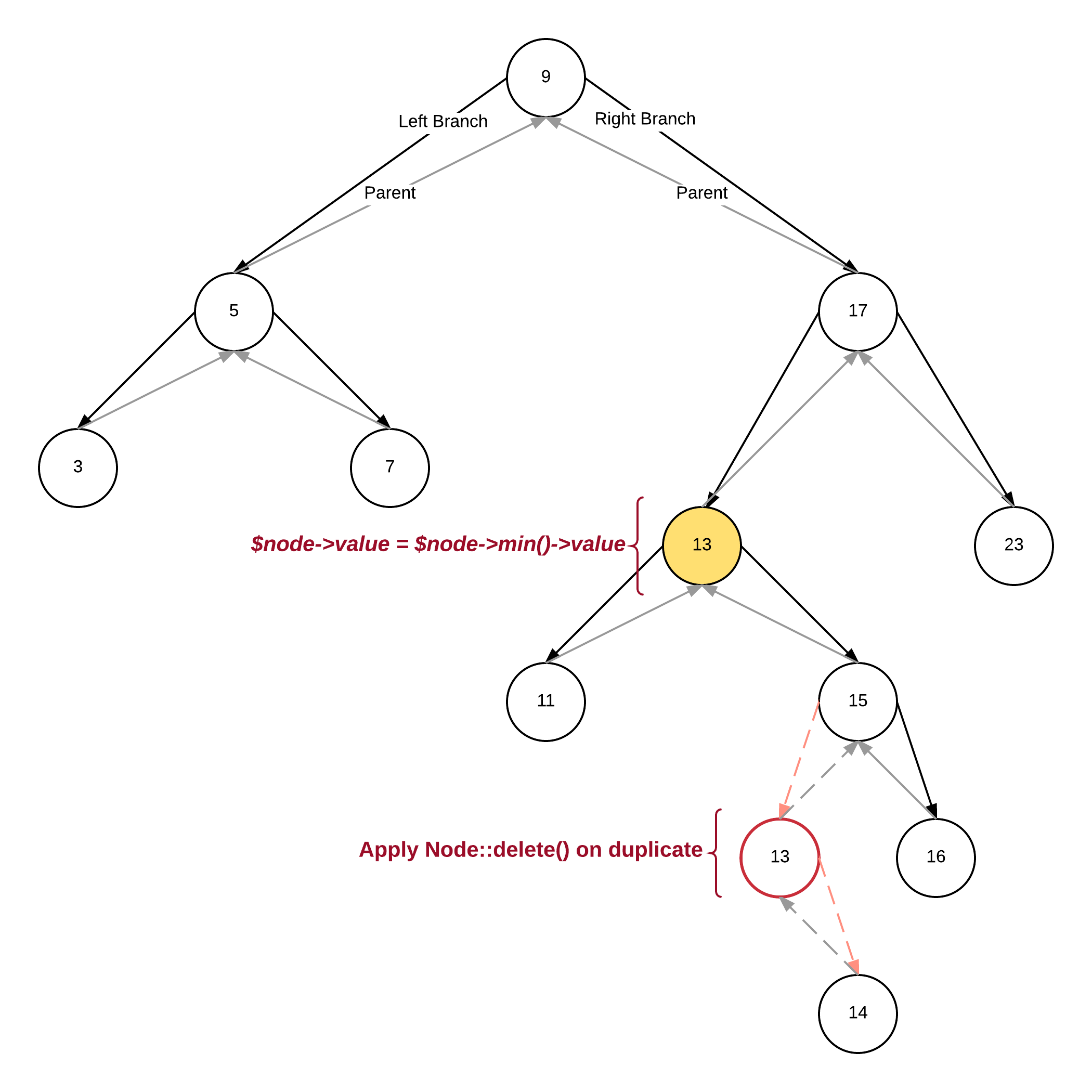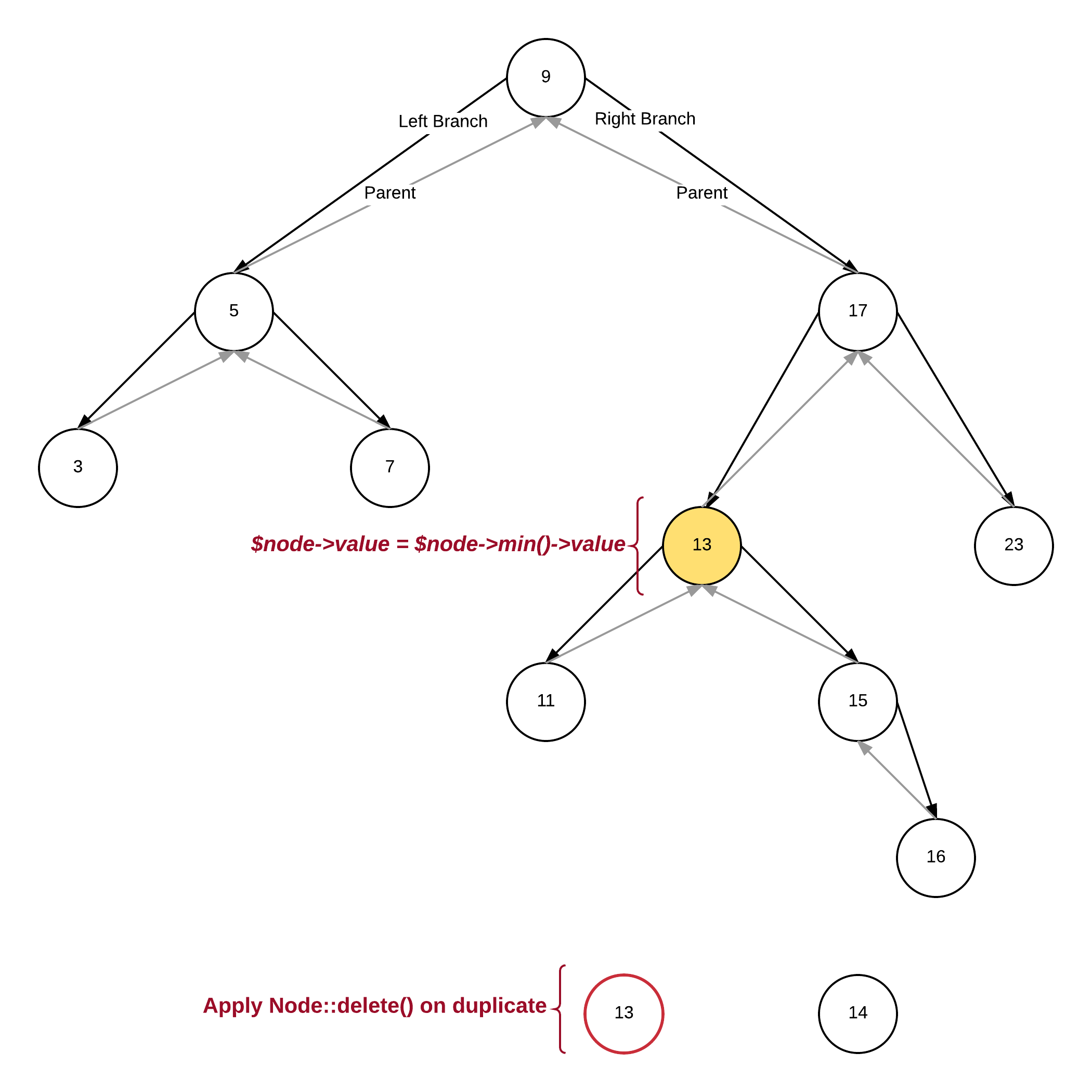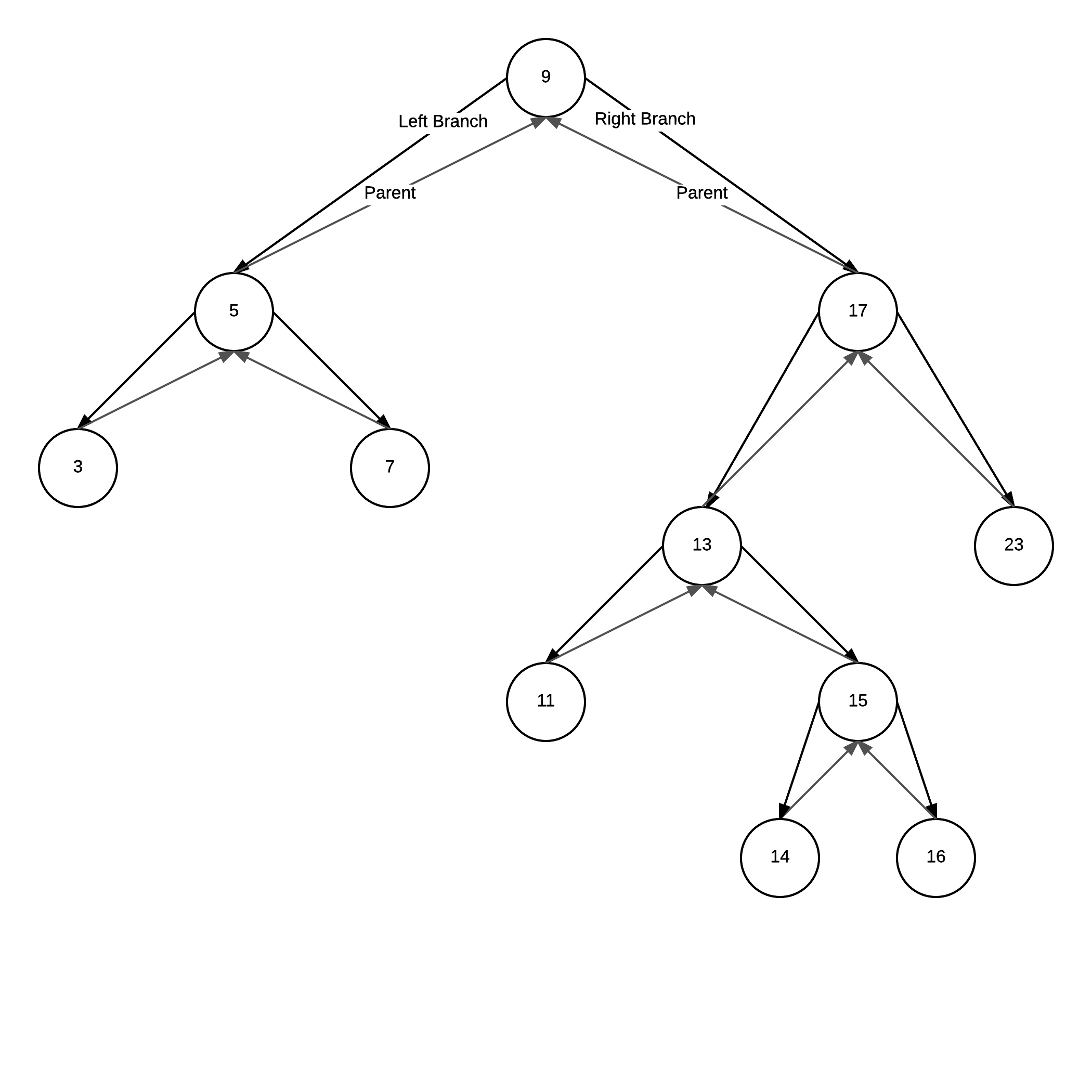
Delete...
3 possible cases:
-
No Children
- Remove the node from the tree
-
1 Child
- Remove the node and replace it with it's child
-
2 Children
- choose either the in-order successor (right sub-trees left most child),
- or the in-order predecessor (left sub-tree's right most child)
- copy that element into the position being removed
The 2 children case is the complex case
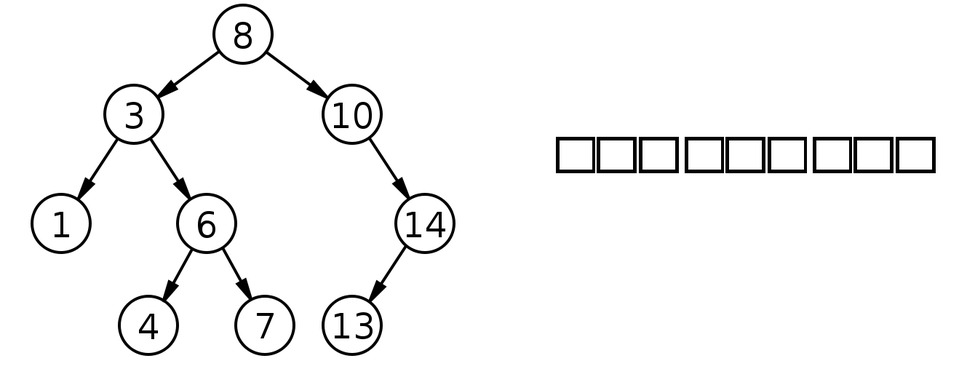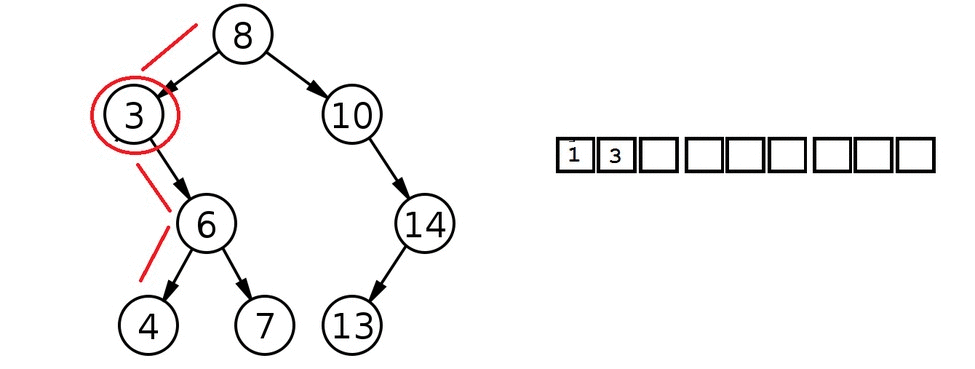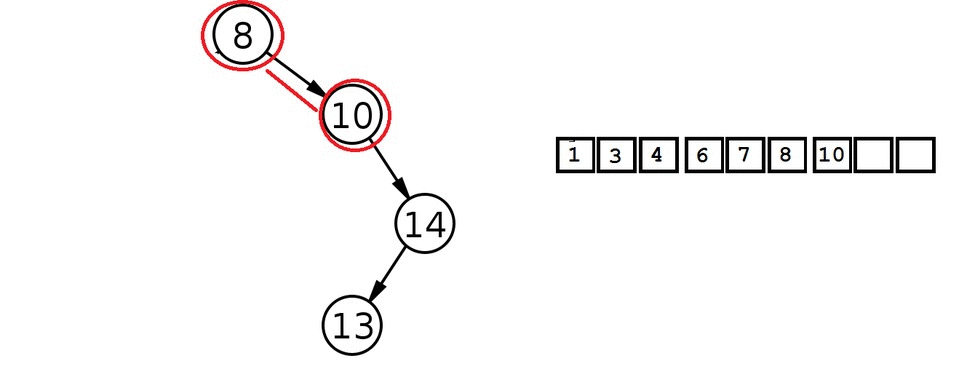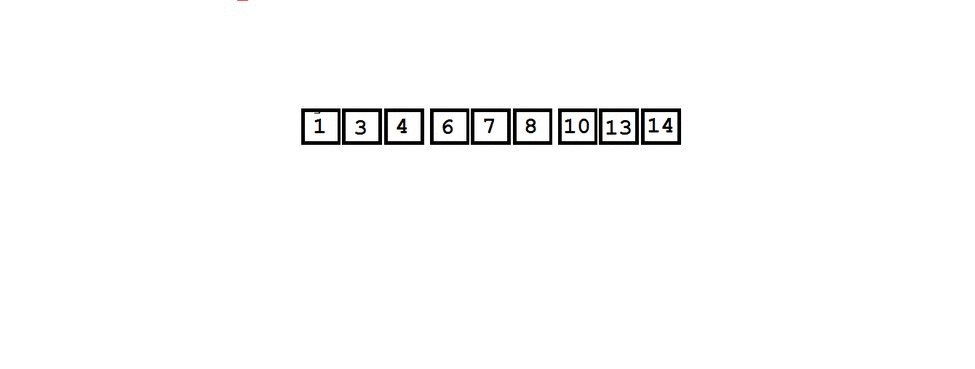
BST In-order Traversal
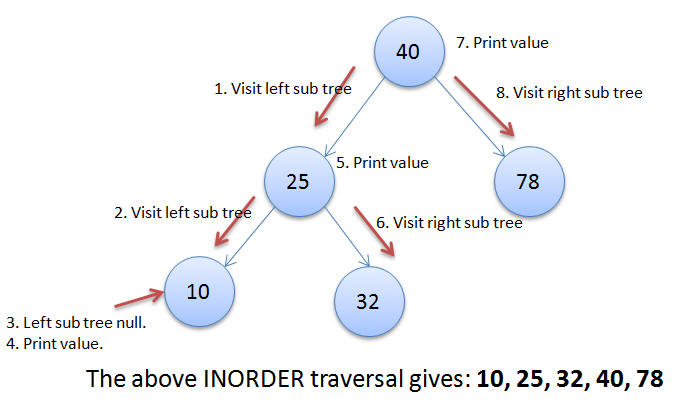
- Traverse left until sub-tree is null
- Print value
- Go right if no left available
Balancing BST
- Grab the middle node, call it the root, and balance from there
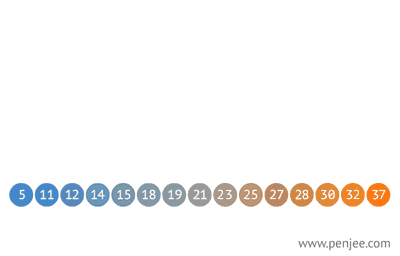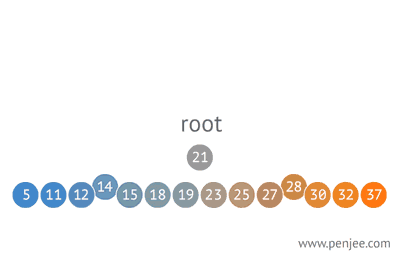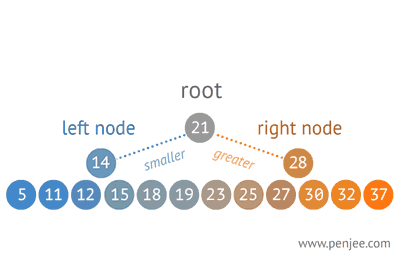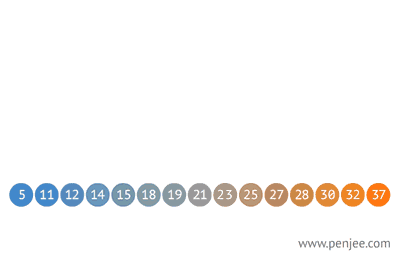
Binary Search Trees
Objectives:
- Define Binary Search Trees (BST)
- Describe Binary Search Algorithm
- Explain an in-order traversal of a BST
- Describe an unbalanced BST
- Describe how to balance a BST