Introduction to Dependent Types
Thomas Dietert
September 26th, 2019
Haskell Hackers Meetup
whoami
- Bay area newbie
- Haskell Enthusiast
- Software Engineer
- Avid Reader
- Aspiring polymath
- Tennis Player
- Rock Climber

- Hiring Haskell Engineers
- Compilers + Custom Hardware + ML
- Email r at groq dot com if interested
The λ-calculus
- Calculus - a particular method or system of calculation or reasoning
- "Invented" by Alonso Church in the 1930s
- expresses computation based on function abstraction and application using variable binding and substitution
The λ-calculus
Syntax
Free Variables
Variables in an expression that are not bound by any lambda abstraction
Bound Variables
Variables in the body of an expression that are bound (captured) by a variable binding in an outer lambda abstraction
α-equivalence
- Terms are structurally equivalent, but not nominally equivalent
- α-conversion replaces all bound variables with fresh variable names
\( \lambda x \rightarrow \lambda y \rightarrow x \quad =_{\alpha} \quad \lambda a \rightarrow \lambda b \rightarrow a \)
\( \lambda x \rightarrow \lambda y \rightarrow x \quad \not =_{\alpha} \quad \lambda a \rightarrow \lambda b \rightarrow b \)
Dynamic Semantics
(evaluation)
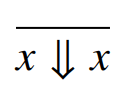
* call by value
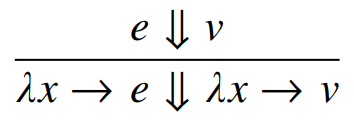
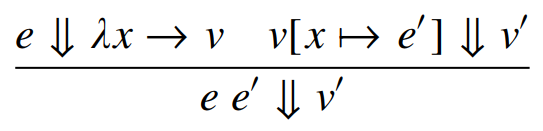
(Capture Avoiding) Substitution
- Happens during \(\beta\)-reduction
- Allows for argument substitution without altering the semantics of the expression
- Uses \(\alpha\)-conversion to avoid free and bound variable naming conflicts
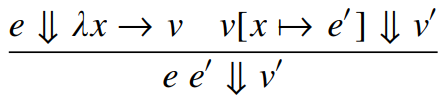
Static Semantics
(type-checking)
???
The Simply Typed
λ-calculus
(STLC)
- Extension of the untyped λ-calculus
- Expressions can have their type annotated
- λ terms must have their types checked
- More static guarantees but still strongly normalizing
STLC Abstract Syntax
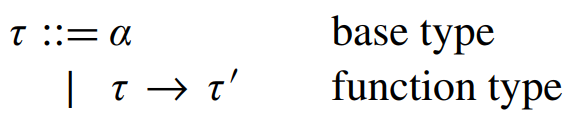

STLC
Dynamic Semantics
(evaluation)
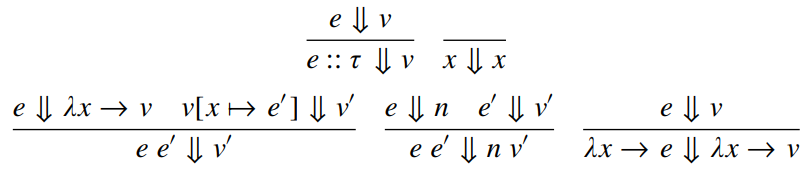
Type Contexts (\(\Gamma\))

STLC
Static Semantics
(type-checking)
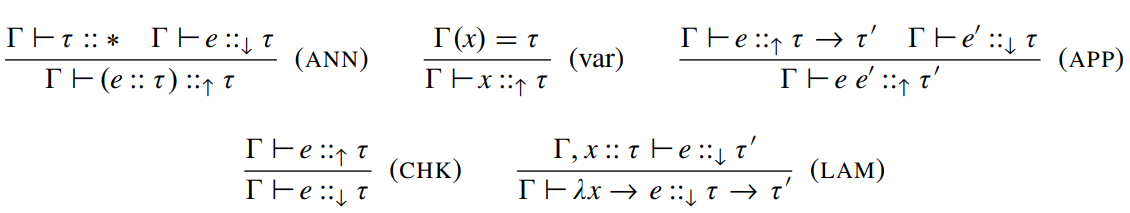
STLC Implementation
(syntax + typechecker)
The
Polymorphic λ-calculus
(System-F)
- Formalizes the notion of parametric polymorphism
- Function types can now be parameterized by type variables
- Type inference becomes undecideable
- Basis upon which GHC's core IR is founded*
"Types indexed by Types"
\( \tau \Coloneqq \dots \mid \Lambda \alpha \rightarrow \tau \mid \alpha \)
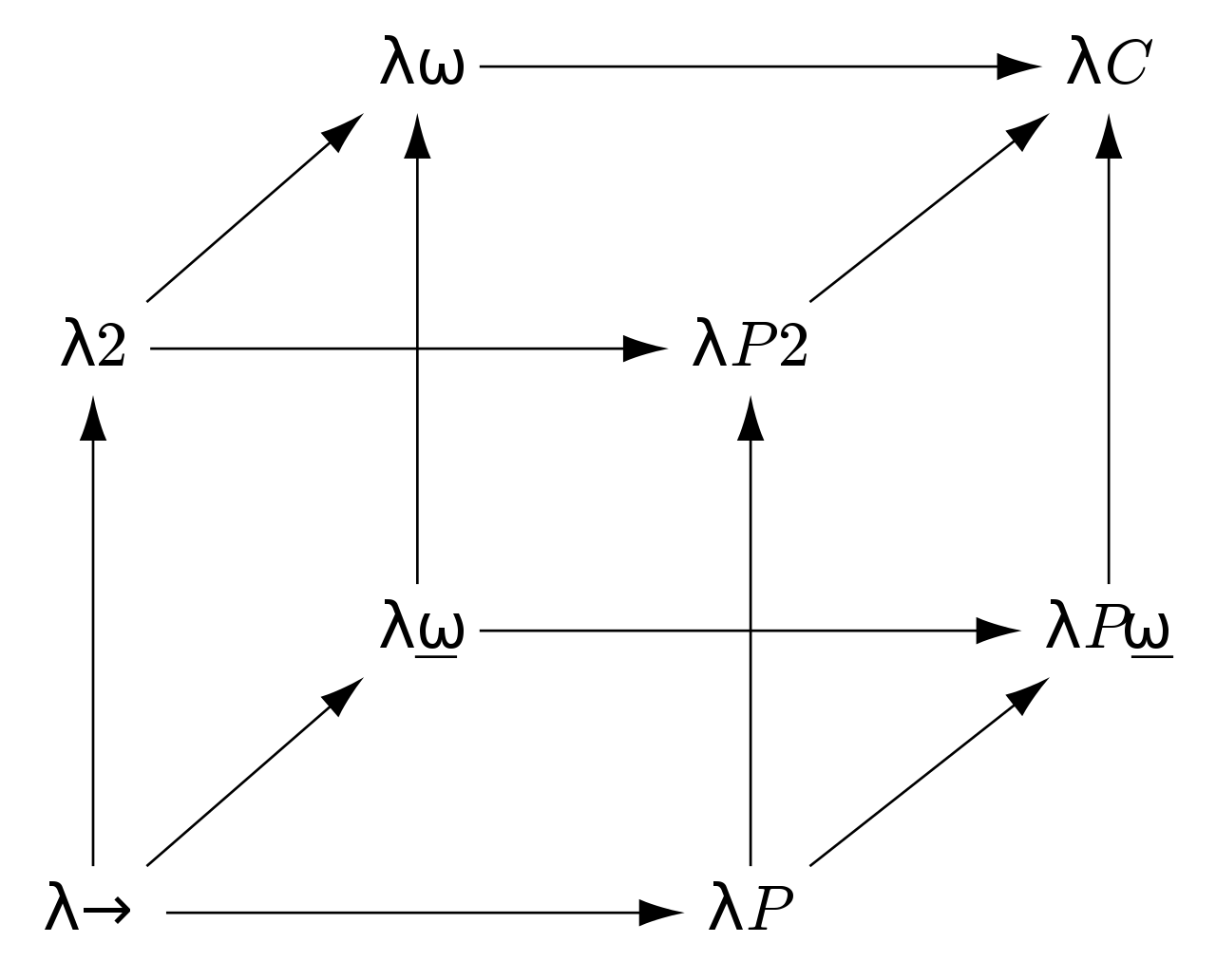
The
Parametric, Polymorphic
λ-calculus
(System-\(F_\omega\))
- Like System-F, but with > 1 kind of types
- Base types can now be parameterized by other types (called "type operators")
- Actual basis upon which GHC's core IR is founded
The
Dependently Typed
λ-calculus
(\( \lambda_{\Pi} \), \( \lambda P \))
- Types can depend on values
- Some computation happens at compile time
- Also formalizes the notion of parametric polymorphism... (types are values)*
"Types indexed by Values"
\( \lambda_{\Pi} \)
Abstract Syntax

\(\lambda_{\Pi} \)
Dynamic Semantics
(evaluation)
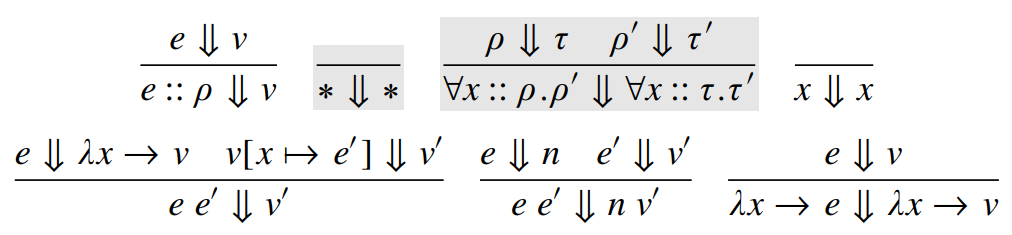
\(\lambda_{\Pi} \)
Dynamic Semantics
(Rule \( \text{VStar} \))
\( \text{VStar} \)
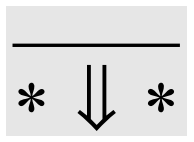
\(\lambda_{\Pi} \)
Dynamic Semantics
(Rule \( \text{VPi} \))
\( \text{VPi} \)
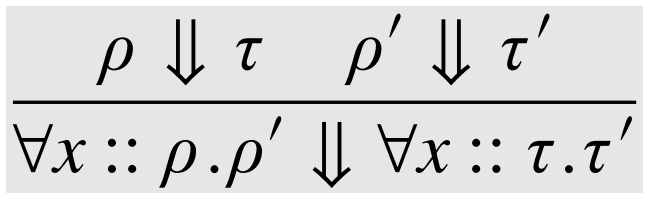
\(\lambda_{\Pi} \)
Contexts
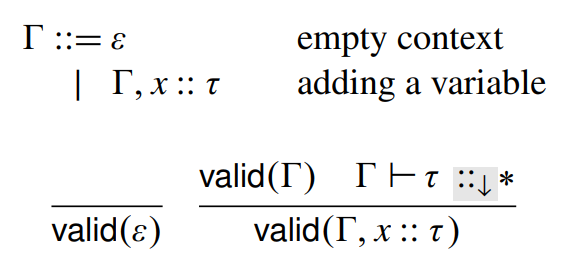
\(\lambda_{\Pi} \)
Static Sematics
(type-checking)

\(\lambda_{\Pi} \)
Static Sematics
(cont.)
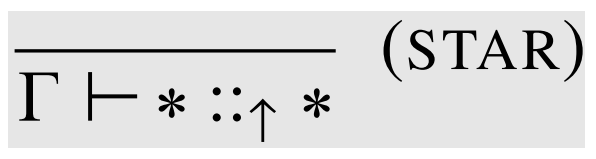
\(\lambda_{\Pi} \)
Static Sematics
(cont.)
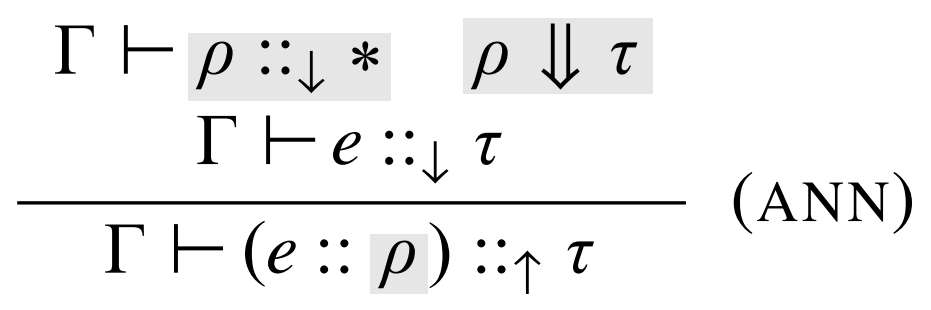
\(\lambda_{\Pi} \)
Static Sematics
(cont.)
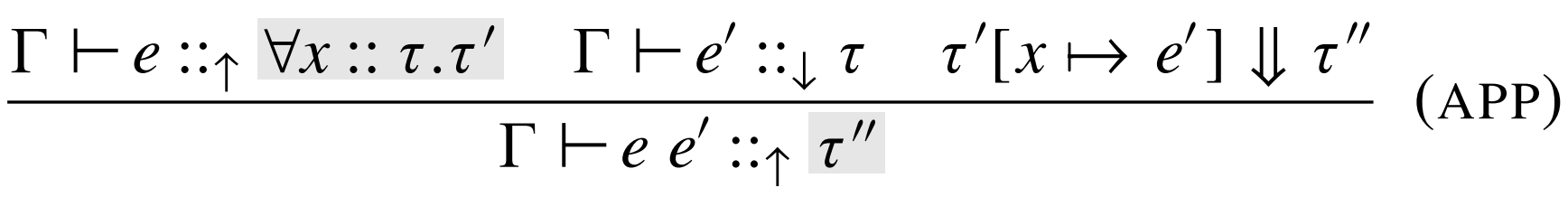
\(\lambda_{\Pi} \)
Static Sematics
(cont.)
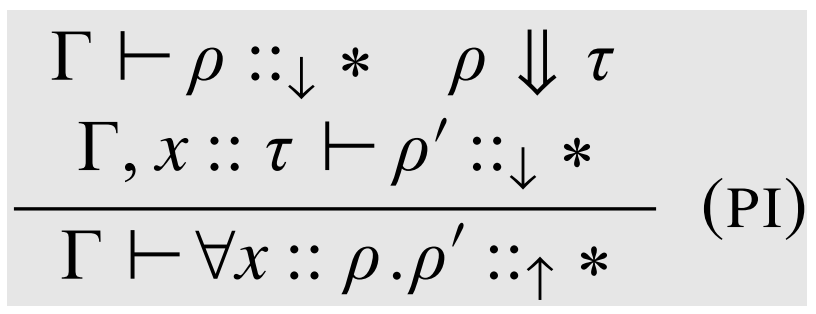
\(\lambda_{\Pi} \)
Static Sematics
(cont.)
\( id = \lambda \alpha \rightarrow \lambda x \rightarrow x \\ :: \forall (\alpha :: *) . \forall (x :: \alpha) . \alpha \)
\(\lambda_{\Pi} \) Implementation
(syntax + typechecker + evaluator)