A Survey of
Dynamic Traffic Assignment
B10902028 王勻
Introduction
Dynamic Traffic Assignment
- Dynamically adjust routes for all vehicles based on traffic condition
- Input: origin-destination pairs
- Output: best route for each O-D pair
Why Dynamic Traffic Assignment?
- Advanced application of connected vehicle
- Mitigate traffic congestion
- Improve traffic & energy efficiency
Preliminary
Wardrop equilibrium
- Based on Nash equilibrium
-
Wardrop's first principle (User Equilibrium)
- \(cost(\text{used route}) \leq cost(\text{unused route})\) for every O-D pair
- No one can lower his cost through unilateral action
-
Wardrop's second principle
- At equilibrium state, average travel time is at a minimum
solving User Equilibrium \(\iff\) optimizing Traffic Assignment
Heuristic Approach
Gawron, C. (1998). An iterative algorithm to determine the dynamic user equilibrium in a traffic simulation model. International Journal of Modern Physics C, 9(03), 393-407.
Traffic Flow Model
- Traditional: NaSc
- Proposed: Queuing Model
- Model network as directed graph \(G(E, V)\)
- Each \(e \in E\) has capacity \(q\), length \(l\) and number of lanes \(\lambda\)
- Vehicles queue when ingoing traffic exceeds the constraints of \(\lambda\) or \(q\)
- Faster simulation of traffic condition with Queuing Model
- \(O((\sum |r|)\log N)\) ?
to simulate real-world traffic
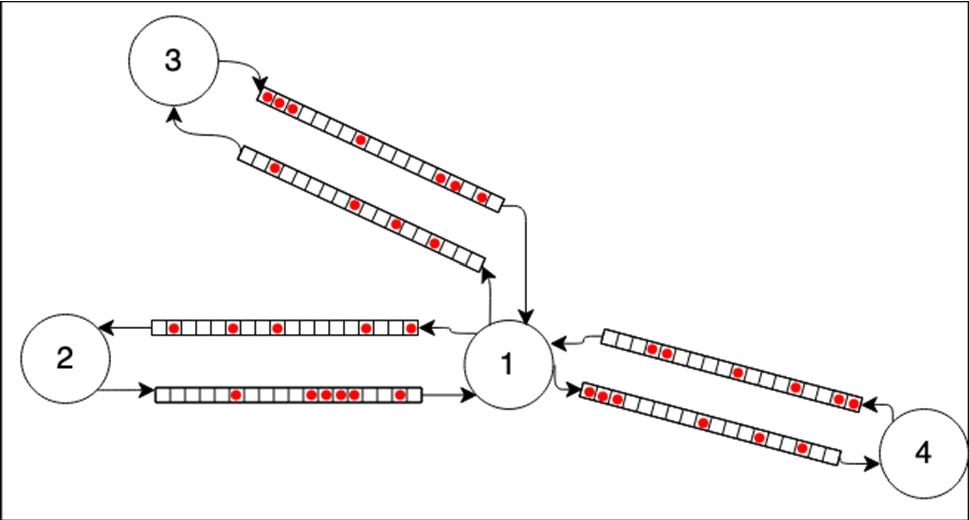
NaSc
Queuing Model
Naive
- Initially assign shortest path to each O-D pair
- Simulate and update traffic condition
- Update shortest path based on last simulation
- Repeat 2~4
Issues
- Route choice may oscillate (convergence is not guaranteed)
Probability-based
- Each driver \(d\) has:
- Departure time \(t_d\), origin \(O_d\), destination \(D_d\)
- A set of candidate routes \(R_d\) (\(=k\) shortest paths)
- Probability distribution \(p_d\) on route set \(R_d\), i.e., \(\sum\limits_{r \in R_d}p_d(r) = 1\)
- Cost function \(c_d\) on route set \(R_d\) (regarding travel time)
Probability-based
- Simulate (based on \(p_d\))
- Each driver \(d\) choose its route based on \(p_d\)
- Update \(p_d\) and \(c_d\)
- Update cost function: (\(c_s(r)\) is based on simulation)
- \(c_d'(r) = c_s(r)\) if \(r\) is chosen by \(d\)
- \(c_d'(r) = \mu c_s(r) + (1 - \mu)c_d(r)\) if \(r\) is not chosen by \(d\)
- Update probability distribution \(p_d\)
- Update cost function: (\(c_s(r)\) is based on simulation)
- Take smallest \(c_d\) route
-
Every user choose his best route
-
Better approach to Wardrop equilibrium
Advantages
Mathematical formulation
- \(v_a\): traffic volume of link \(a\)
- \(S_a(x)\): link \(a\)'s average travel time at traffic volume \(x\)
- \(\alpha_{ij}^{ar}\): (binary) whether link \(a\) is on route \(r\) from \(i\) to \(j\)
- \(x_{ij}^r\): traffic of route \(r\) from \(i\) to \(j\)
- \(T_{ij}\): traffic demand from \(i\) to \(j\)
Definition
Minimize
- total travel time
- \(\sum\limits_a\int^{v_a}_0S_a(x)dx\)
Subject to
- link volume = total route traffic containing the link
- \(v_a = \sum\limits_i\sum\limits_j\sum\limits_r\alpha_{ij}^{ar}x_{ij}^r\)
-
O-D pair traffic = total traffic of all O-D route
- \(T_{ij} = \sum\limits_rx^r_{ij}\)
-
basics
- \(v_a \geq 0,\ x^r_{ij} \geq 0\)
Nonlinear Programming
- \(v_a\): traffic volume of link \(a\)
- \(S_a(x)\): link \(a\)'s average travel time at traffic volume \(x\)
- \(\alpha_{ij}^{ar}\): (binary) whether link \(a\) is on route \(r\) from \(i\) to \(j\)
- \(x_{ij}^r\): traffic of route \(r\) from \(i\) to \(j\)
- \(T_{ij}\): traffic demand from \(i\) to \(j\)
-
Frank-Wolfe algorithm (constrained convex optimization)
Nonlinear Programming
-
Low convergence rate
-
For static traffic assignment only
Issues
Future work
-
Study state-of-the-art algorithm
-
Comparison between different approaches
-
Implementation & Evaulation ?