Κρυπτογραφία

03t 與他的肝

| |

小提醒

不要摔電腦 QQ

不要中暑 QQ

可能學到的東西

0

1. 密碼與它的歷史雜碎唸

* 以史為鏡，可以知興替。密碼學歷史簡介！

2. 加密與編碼系統淺淺談

* 你知道密碼、編碼、雜湊差在哪裡嗎？就讓我們一探究竟。

3. 深埋於土裡的智慧結晶

* 凱薩老兄啊，你這加密也太好破解了吧，換一個啦！

4. 迅速確實的對稱式加密

* 電腦時代，我們需要學習電腦訊號的加密方式！

5. 無堅不摧的公鑰加密法

* 哇，毀了。我們被竊聽了，怎麼辦？

6. 電腦世界的防偽與防盜

* 什麼是電子簽名？與密碼學何干？

7. 量子物理學將何去何從

* 暴力破解法與它的剋星！淺談後量子加密與它的神秘。

預告

今天這堂課一定會講不完

所以來投票吧！

我想要 ...

https://forms.gle/c8zqiUJbA6cqYB4u8

那就快開始吧！

希望不會太難 QQ

https://ppt.cc/foOZAx

密碼與它的

歷史雜碎唸

1 讓我們坐上時光機

上古時代

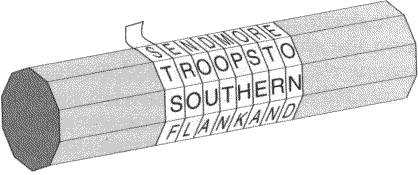
古希臘密碼棒棒

上古時代

卡爾達諾漏格板板

上古時代

密碼盤盤

傑弗遜圓盤

上古時代

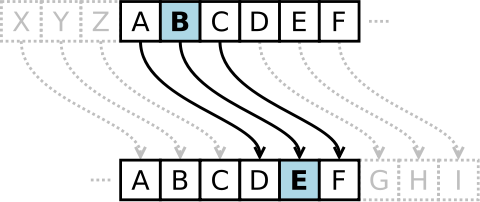
凱薩加密

中世紀

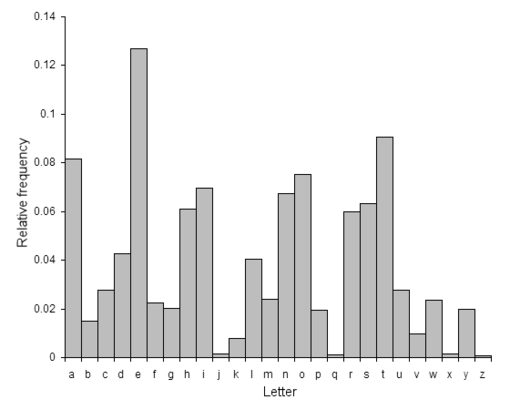
替換式加密 vs 頻率分析方法

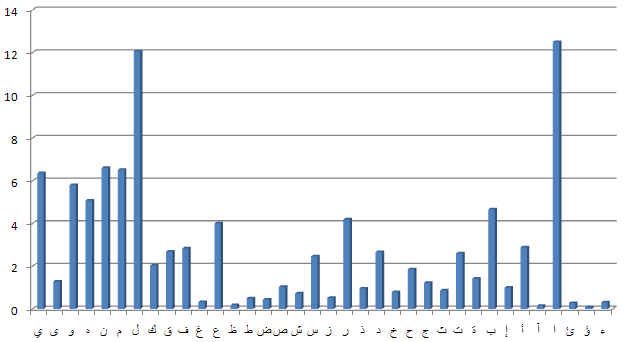
Risalah fi Istikhraj al-Mu'amma

中世紀

漏字文

中世紀

多表替換加密 & 一次性密碼本

近代與現代

恩尼格瑪密碼機

這裡有詳細原理

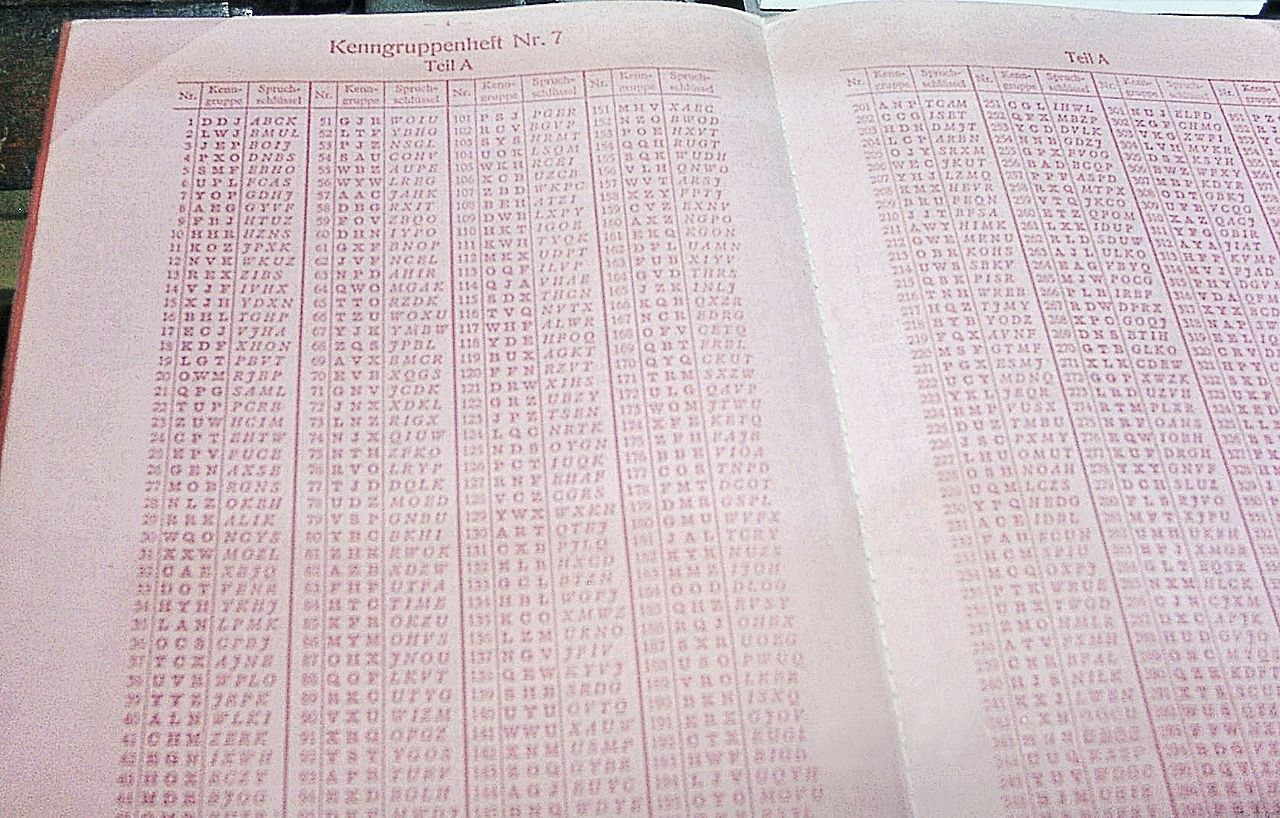
近代與現代

DES & AES

近代與現代

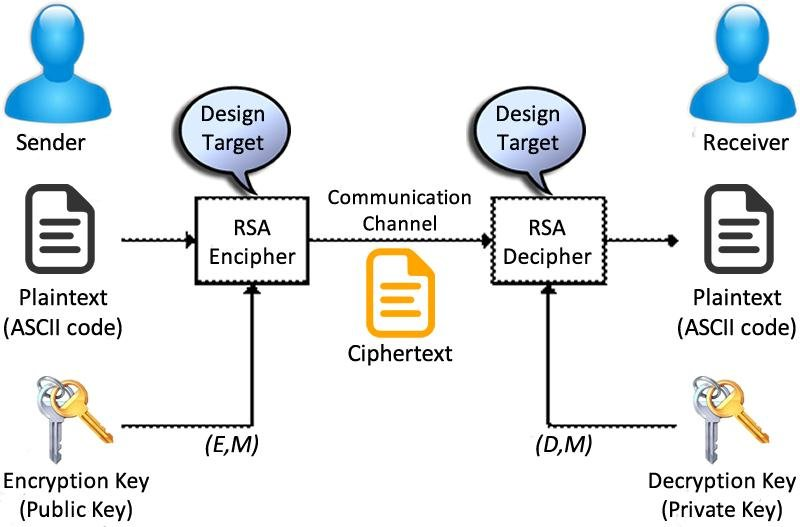
RSA 演算法

未來

量子加密

下一個等你發明吧！

加密與編碼

系統淺淺談

2 密碼學是什麼

- 不是研究怎麼設安全的密碼
- 不是教你怎麼破解別人Facebook

- 你不會因為知道密碼學在幹嘛而成為天才駭客

- 一堆數學

. ~~可是我不會數學，所以今天講的不多 QQ~~

- 如果已經沒興趣了

. 可以找隊輔聊天或做你的成發 XD

密碼學的分類

- 古典密碼學

* 資料保密、傳遞

* 密碼破譯

- 現代密碼學

* 古典密碼學所有東西

* 資料完整性驗證 (data integrity)

* 資料的不可否認性 (non-repudiation)

* 雜湊、亂數、隱寫術

常用詞彙解釋

- 加密 . 解密 (encrypt / decrypt)

* 雙向變換

* 需要金鑰，不知道金鑰即無法加解密

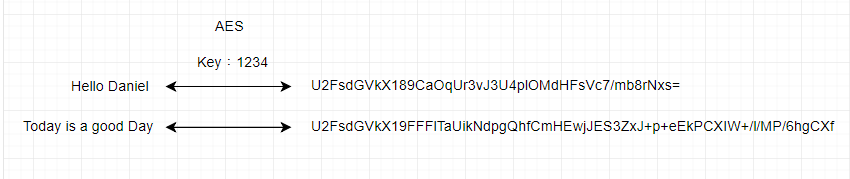
常用詞彙介紹

- 明文 (plain text)

* 未經過加密的文字

- 密文 (cipher text)

* 加密後產生的文字

- 金鑰 (key)

* 加解密所需要的東西

- 演算法 (algorithm)

* 解決複雜問題的一連串步驟

易混詞彙解釋

- 編碼 . 解碼 (encode / decode)

* 雙向轉換

* 不需金鑰，演算法公開

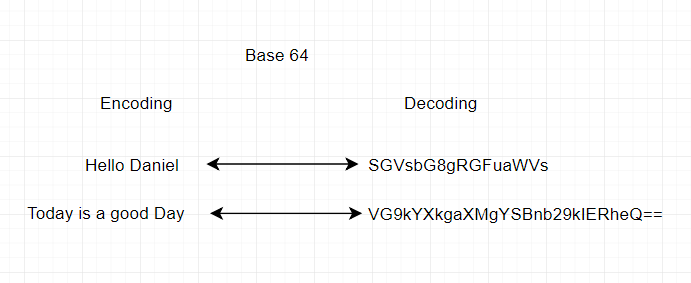
試試看！

- 編碼 . 解碼 (encode / decode)

1. Unicode：\u9019\u662f\u842c\u570b\u300c\u7de8\u78bc\u300d

2. UTF-8：\xe9\x80\x99\xe6\x98\xaf\x55\x54\x46\x2d\x38\xe7\xb7\xa8\xe7\xa2\xbc

3. Base64：

6YCZ5pivQmFzZTY057eo56K8

易混詞彙解釋

- 雜湊 (hash)

* 單向轉換

* 相同字串的雜湊必相同

* 相同雜湊有極低機率是不同字串

試試看！

- 雜湊 (hash)

1. SHA256：

fb5e724552e4d9a2573ef5a3b0885b369775664903d323ae9adb80c765c28797

2. SHA-1：

2354d0dcc1904923bd09f65cdf02c184bcb09031

3. ripemd160：

c619a42fc6f6e28fa04b330bd3634ebdab472636

不要弄混了喔 XD

深埋於土裡

的智慧結晶

3 凱薩加密

Caesar Cipher

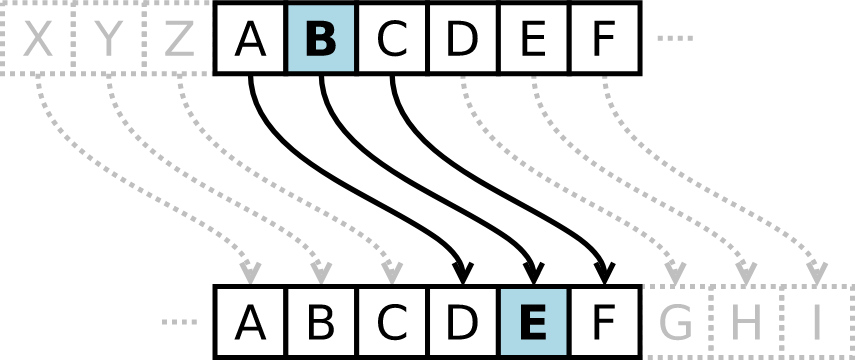
凱撒密碼的替換方法是將明文字⺟表向左或向右移動一個固定數目的位置成為密文。

Key：+3

凱薩加密

Caesar Cipher

是不是很簡單呢？當然，如果我們將英文字⺟編碼：

\(A=0, B=1, C=2...\)

則這個密文與明文的關係可以用以下數學式子表示：

\(C_i = (P_i + key) \bmod 26\)

這時候你只要枚舉一下 \(key\)，很快就可以破譯了。

小試身手

Caesar Cipher

破解以下凱薩加密：

Tq lqhafy lzak lwpl, qgm sjw kwllafy qgmj imsdaxqafy lqhafy khwwv.

被嫌太簡單 QQ：

Va pelcgbtencul, n Pnrfne pvcure, nyfb xabja nf Pnrfne'f pvcure, gur fuvsg pvcure, Pnrfne'f pbqr be Pnrfne fuvsg, vf bar bs gur fvzcyrfg naq zbfg jvqryl xabja rapelcgvba grpuavdhrf.

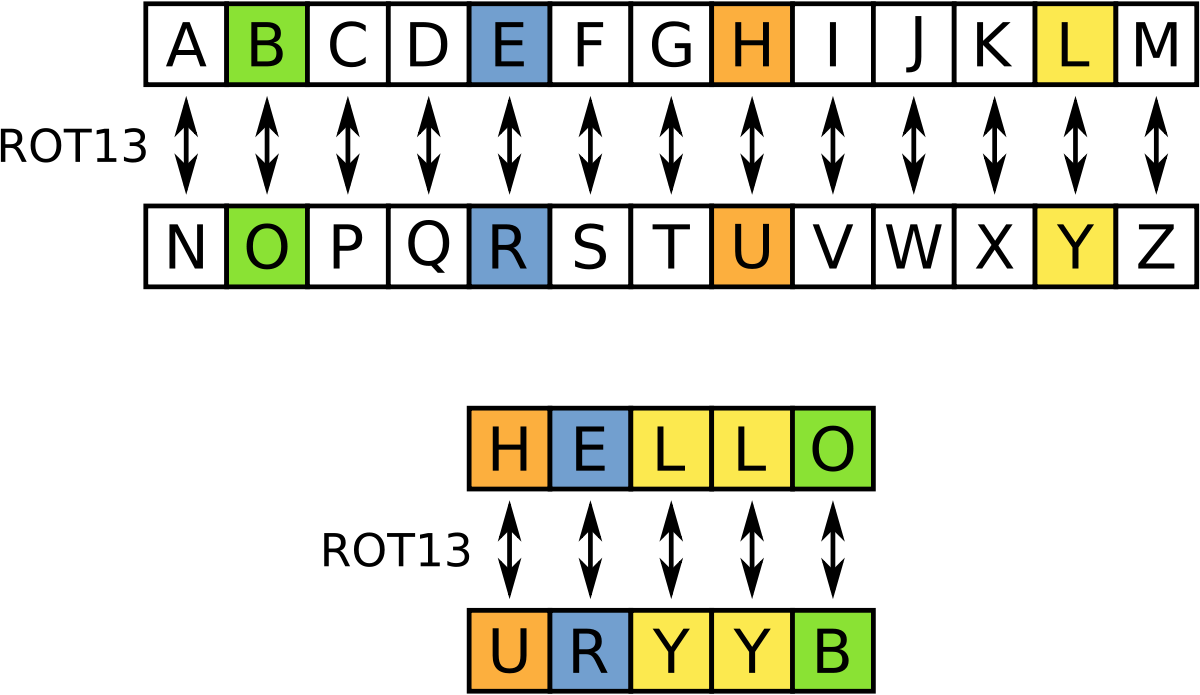
ROT 13

Caesar Cipher

\(Key = 13\) 的凱薩加密又叫作 ROT 13

替換式加密

Substitution Cipher

凱薩實在太好破解了 QAQ

所以有人發明這種替換式加密方式，雖然對電腦根本只是小Case，但以前要破解就要用語言分析了。

替換式加密

Substitution Cipher

替換式加密的Key就是整張替換表

凱薩加密、ROT 13也是一種替換式加密

就連這樣也是：

小試身手

Substitution Cipher

破解以下替換式加密：

Uvcrhlb uzdumhmzmhvl xhpfgt wgxtepmhvl hu rgte gsue, hul’m hm?

太簡單？

pmo cwlqa tnsfi zse kwdrh svon pmlnpooi xugb ysjh

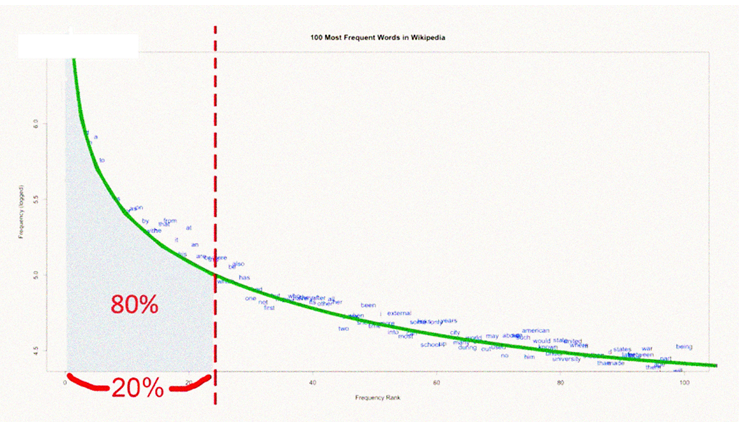
齊夫定律

Zipf's Law

齊夫定律(Zipf's law) 說明了事物出現頻率與名次呈現反比關係。

自然界有許多事物是滿足齊夫定律的，例如英文字⺟出現頻率、單字出現頻率......

維吉尼亞加密

Vigenère Cipher

維吉尼亞加密也是凱薩加密的一種增強。

維吉尼亞加密通常會有個字串\(K\)，做為加密用的偏移量，將原始明文與字串\(K\)一一對應做相加而得到密文。如果字串\(K\) 太短則將不斷重複使用。

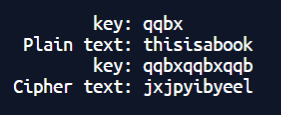
維吉尼亞加密

Vigenère Cipher

寫成數學式子就變成這樣：

\(C_i = (P_i + K_{i \bmod L}) \bmod 26\)

不知道偏移量字串⻑度的就只能亂猜了，除非你是語言學或密碼學大電神。

小試身手

Vigenère Cipher

破解以下維吉尼亞加密：

Ipkn ua lczohomv'c zmdylubo ntqxa?

提示：偏移量四個字母

Yhkx fo isw wkrv ty ict? S’h niui uowi eaui.

提示：偏移量是某種食物

書碼

Book Cipher

書碼是一種利用書本的頁碼、行號、第幾個字來進行編碼的密碼系統，前提是解密者要有那本書。

書碼

Book Cipher

以下是一個書碼的編碼示範

以 Introduction to Algorithms, Third Edition

這本書為例：

~~不相信的話上面的連結可以點~~

小試身手

Book Cipher

破解以下書碼：

為了確保大家都有這本書，這裡給個書名

書名：Tyeczofnetzy ez Wtyrftdetnd - FNWL Wtyrftdetnd

(61.33.9) (111.26.4) (15.20.14) (164.12.13) (39.5.9) (115.14.4)

想知道更多嗎

礙於時間因素

我們必須進入下一個主題了 QQ

其實還有 XD

GKI0TKE6LS9WTEL2YV5AF29AFDRRS29PL2YOFDRBYT8HGNNYRNJ0EKGMGZATAR5HV3I1RNLKV1IOFYZJE210FMVBNELLNY91T3G9T2KKTELRYM==

迅速確實的

對稱式加密

4 資料的編碼

資料在電腦的編碼方式為二進位 (Binary) 編碼，所以不管是中文、英文或任何國家的語言都可以轉換成數字儲存下來。

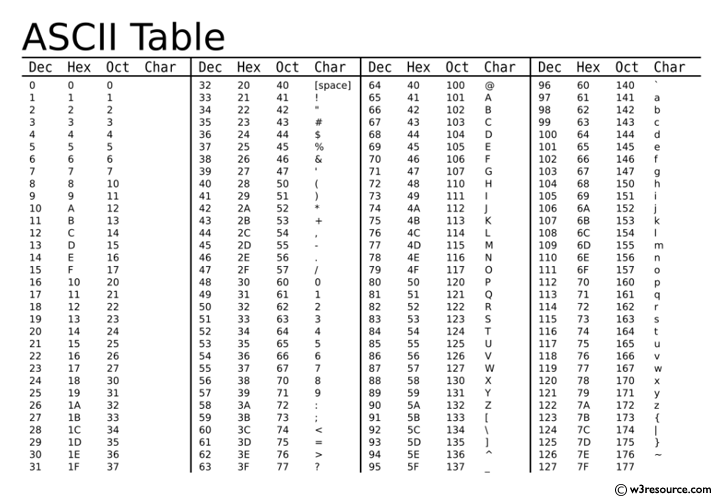
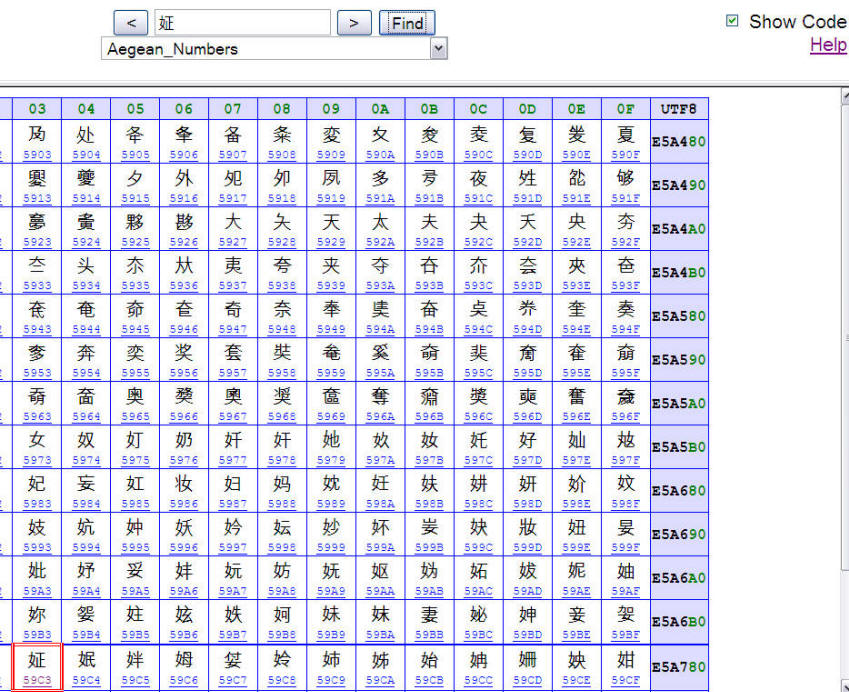
資料的編碼

因此在電腦世界中，資訊傳遞的加密也只要對這些編碼過後的數字進行加密即可。

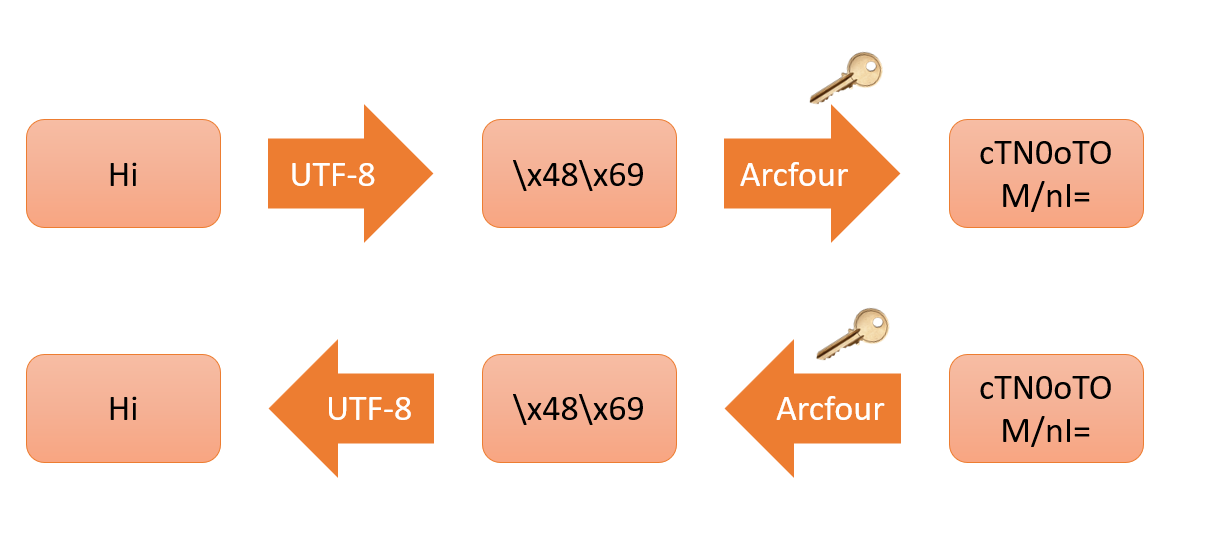
110101001010100101 ...

位元互斥或

互斥或是一個把數字搞得面目全非的方法

觀察以下規律：

\(1234⊕7122 \rightarrow 8669\)

\(5687⊕7122 \rightarrow 13089\)

\(1487⊕7122 \rightarrow 8384\)

\(2587⊕7122 \rightarrow 12052\)

位元互斥或

互斥或(XOR)是一個二元邏輯運算

位元互斥或是將數字每個位元XOR起來

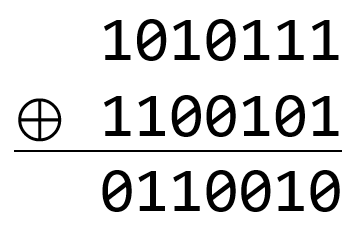
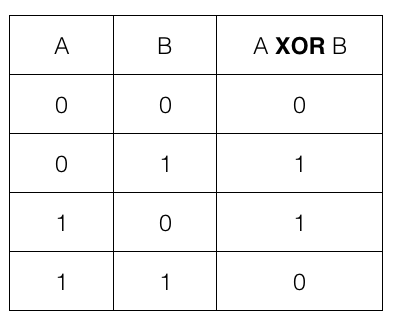
eXclusive OR

bitwise XOR

位元互斥或

當XOR作用在正整數集合時有許多重要性質：

1. \(a ⊕ 0 = a\)

2. \(a ⊕ a = 0\)

3. \((a ⊕ b) ⊕ c = a ⊕ (b ⊕ c)\)

4. \(a ⊕ b = b ⊕ a\)

位元互斥或

當你收到右邊的密文時，幾乎無規律得已出左邊的明文。

\(X⊕Key = 5487\)

\(X =\ ???\)

但若你知道\(Key\)的值是多少，就可以輕易快速的解密出明文來。

\(X =5487 ⊕ Key\)

位元互斥或

與維吉尼亞加密一樣，需要一組由金鑰\(K\)生成的字串\(S\)

進行加密的時候將運算改為 Bitwise XOR 即可。

string plaintext = "ABCDE", key = "JIZZ";

string encrypt(){
    string res = plaintext;
    for(int i = 0; i < plaintext.length(); i++){
    	res[i] ^= key[i % key.length()];
    }
    return res;
}

串流加密 vs 分組加密

- 串流加密 (stream cipher)

* 像 XOR 加密這種以金鑰生成的字串長度和明文長度相等，然後將兩字串一一對應順次加密的方法

- 分組加密 (block cipher)

* 資料加密標準 (Data Encryption Standard, DES)

* 3DES

* 進階加密標準(Advanced Encryption Standard, AES)

資料加密標準

DES 是一連串複雜的加密的過程，1976 年被美國聯邦政府的國家標準局確定為聯邦資料處理標準。所有資料在加密傳輸之前，要先以每64bit分成許多小塊，然後再用已知的56bit金鑰對每一塊進行加密。

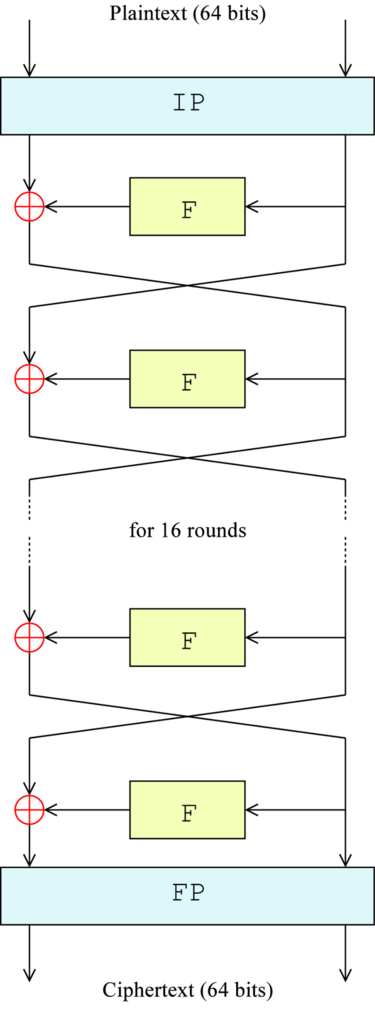
Note：

接下來會有一堆噁心變換

不要問我為啥是這樣

因為這是人訂的標準

資料加密標準

初始置換 IP

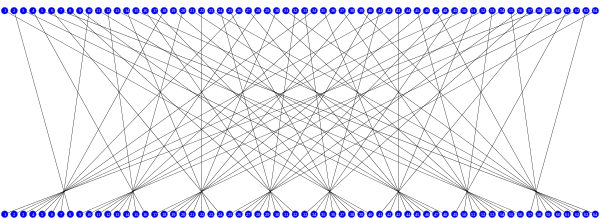
最終置換 FP

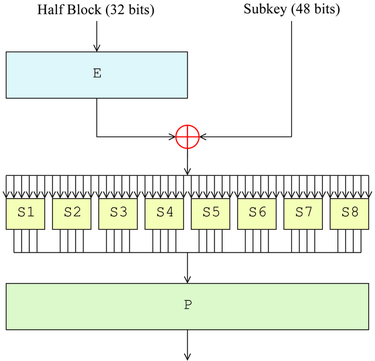
費斯妥函式 F

資料加密標準

費斯妥函式 F

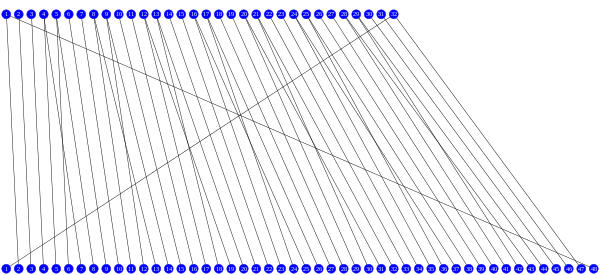
擴張函式 E

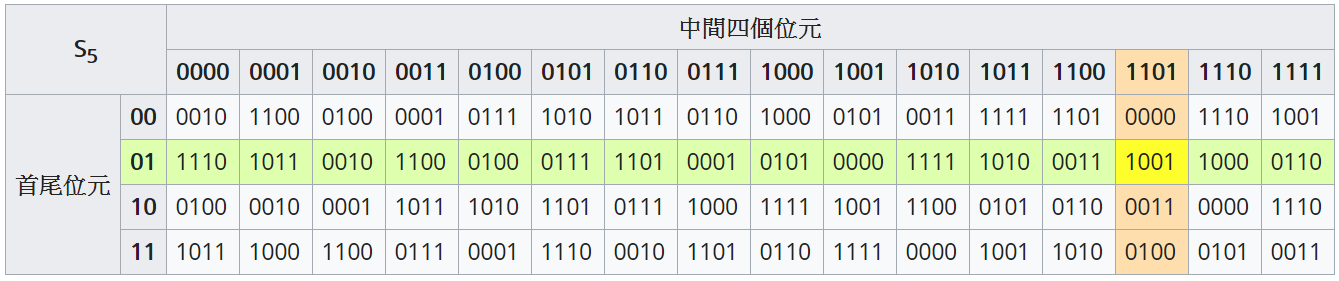
八個不同的S盒

置換盒 P

資料加密標準

金鑰排程

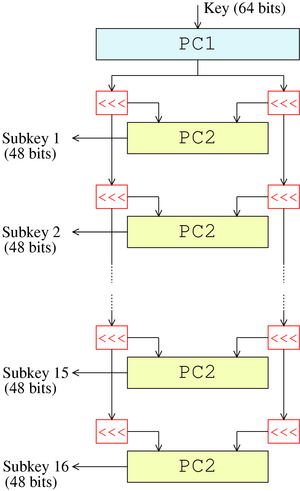
選擇置換1 PC1

56 bits

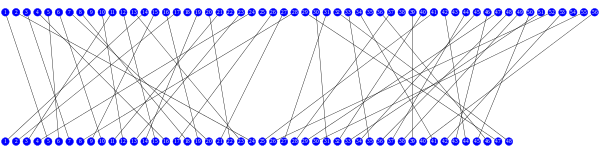
選擇置換2 PC2

移位 <<<

資料加密標準

複習得啦

置換/函數	位置或功能	輸入位元	輸出位元
IP	DES初始變換	32	32
FP	初始變換的反變換	32	32
E	F函式內的擴張運算	32	48
S	讓輸出不要呈線性	6	4
P	使所有S盒都被用到	32	32
PC1	選出有用的56位元金鑰	64	56
PC2	選出每回合的金鑰	56	48

休息一下

好累喔 QQ

暴力破解預防

由於DES的金鑰⻑度僅僅56位元，總共只有 \(2^{56}\) 種組合，以現今的電腦技術在一天內枚舉所有可能的金鑰破解已經不是問題，所以有以下幾種方法來改進DES的強度。

暴力破解預防

你說56位元太少？那就加⻑啊！

可惜配合DES設計的硬體根本不相容這麼⻑的金鑰，所以再想想其他辦法吧 QQ

暴力破解預防

那就兩個DES串在一起總行了吧。這樣要同時將兩個金鑰枚舉正確，夠難了吧。

假設你有學過演算法的話，你會發現兩個根本不是問題，你可以拿中途相遇 (Meet in the Middle) 演算法輕鬆破掉，頂多枚舉時間變成兩倍而已。

暴力破解預防

於是3DES就誕生了，沒錯，它就是三個DES串在一起，不但硬體支援加速，而且也不容易被暴力破解掉。

暴力破解預防

注意，這裡三個DES的金鑰要是不同的金鑰，不然與一個單純的DES沒兩樣。

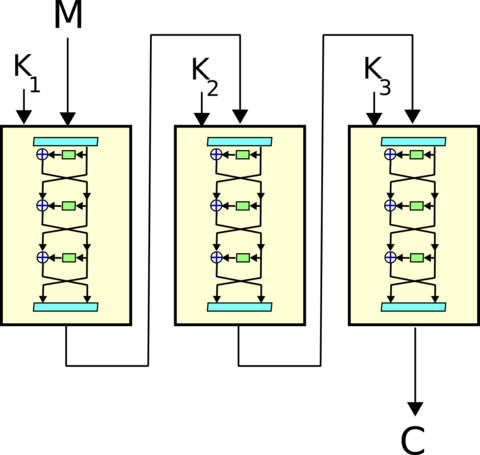
進階加密標準

2002年，AES取代了DES，成為美國聯邦政府採用的一種區段加密標準。到了2006年，它已然成為對稱金鑰加密中最流行的演算法之一。

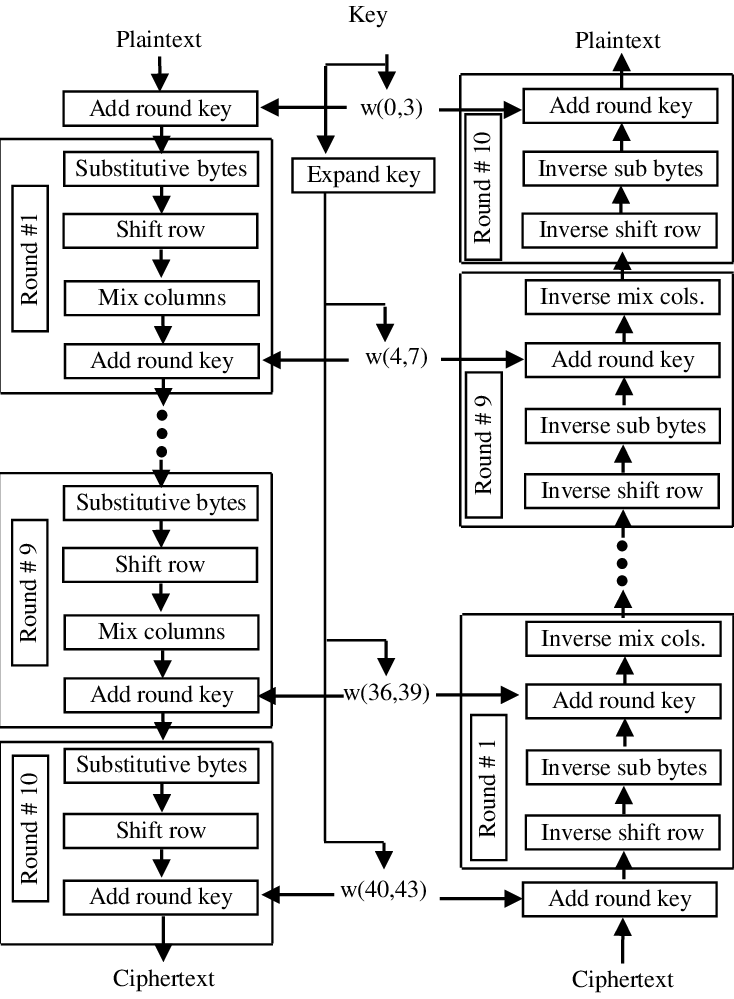
進階加密標準

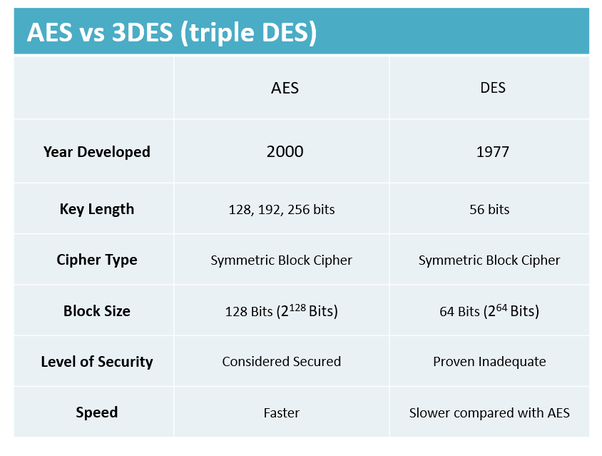
AES的明文區段必須要是128位元

128位元密鑰版本有10個加密迴圈，

192位元版本有12個，256位元版本有14個。

進階加密標準

這個演算法會以明文的16個位元組先放成\(4\times4\)的矩陣

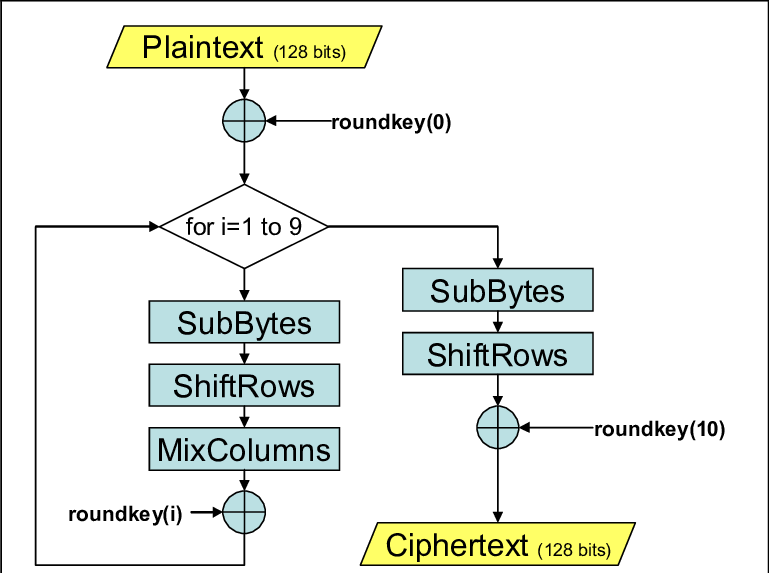
- AddRoundKey

- SubBytes

- ShiftRows

- MixColumns

進階加密標準

AddRoundKey

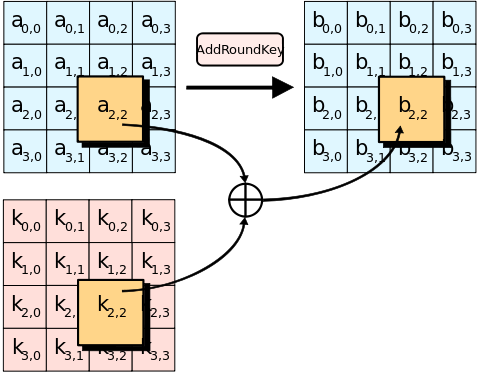
原矩陣 ⊕ 回合金鑰

進階加密標準

SubBytes

S盒又出現啦

這次是AES S-box

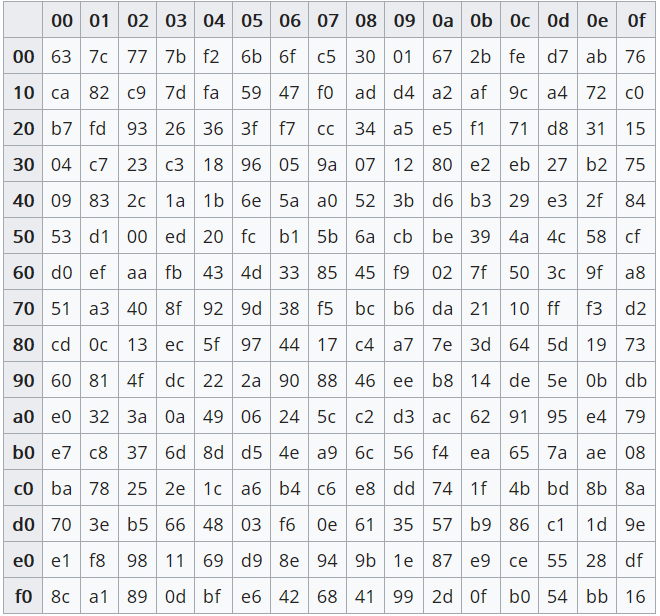
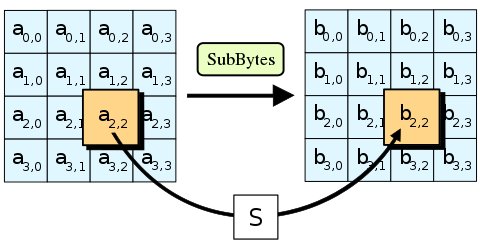
進階加密標準

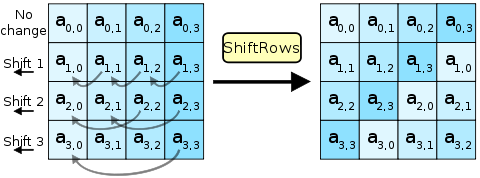
ShiftRows

進階加密標準

MixColumns

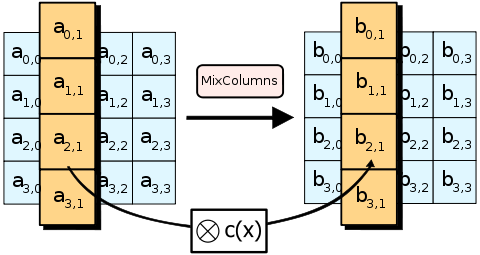
將每一列的四個元素分別當作\(1, x, x^2, x^3\)的係數，接著將此多項式和一個固定的多項式\(c(x) = 3x^3 + x^2 + x + 2\)在模\(x^4 + 1\)下相乘，得到新的係數就是新的位元組值。

進階加密標準

金鑰排程

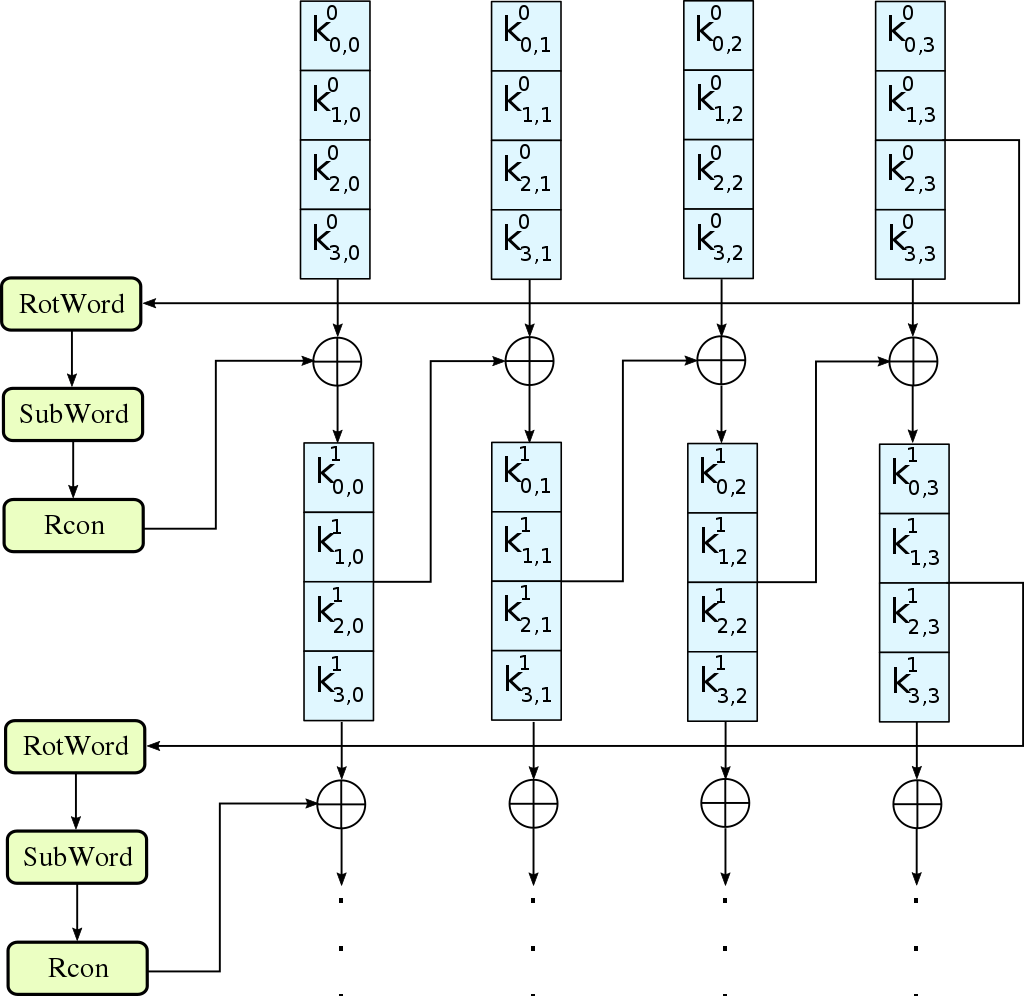
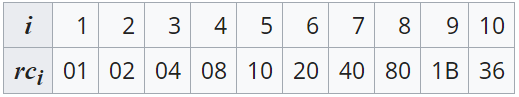
Rcon

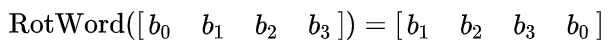
RotWord

SubWord

資料加密標準

複習得啦

步驟	功能	位置
AddRoundKey	與回合金鑰XOR	每個加密迴圈
SubByte	讓輸出不要呈線性	每個加密迴圈
ShiftRows	動起來	每個加密迴圈
MixColumns	一個奇怪的多項式乘法	最後一個沒有
RotWord	動起來	金鑰排程
SubWord	讓金鑰不要呈線性	金鑰排程
Rcon	規定好的回合常數	金鑰排程

休息一下

好累喔 QQ

是說RSA咧

等一下就有了啦

無堅不摧的

公鑰加密法

5 哪裡怪怪的

- 加密 . 解密 (encrypt / decrypt)

* 雙向變換

* 需要金鑰，不知道金鑰即無法加解密

Internet

You

Stranger

哪裡怪怪的

那就傳給他？

Internet

You

Stranger

哪裡怪怪的

那就傳給他？

Internet

You

Stranger

Eavesdropper

哪裡怪怪的

非對稱式加密！

Internet

You

Stranger

Eavesdropper

哪裡怪怪的

非對稱式加密！

Internet

You

Stranger

Eavesdropper

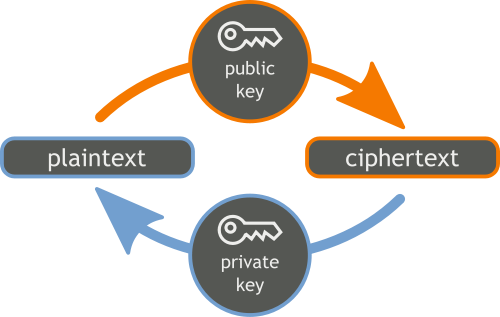
非對稱式加密

- 非對稱式加密

* 加密、解密金鑰不同

* 公鑰：類似鎖頭，用以加密

* 私鑰：類似鑰匙，用以給自己解密

非對稱式加密

- 非對稱式加密

* 必須保證無法依鎖打造鑰匙

* 也就是無法只憑公鑰取得私鑰

RSA演算法

說起非對稱式加密，許多人的第一印象應該就是RSA了吧。

RSA是1977年由Ron Rivest、Adi Shamir和Leonard Adleman一起提出的，所以被稱作RSA演算法。

RSA的理論基礎是來自質因數分解的困難度，如果有人找到了一個快速分解大整數的算法，那RSA可能就無法保證安全性了。

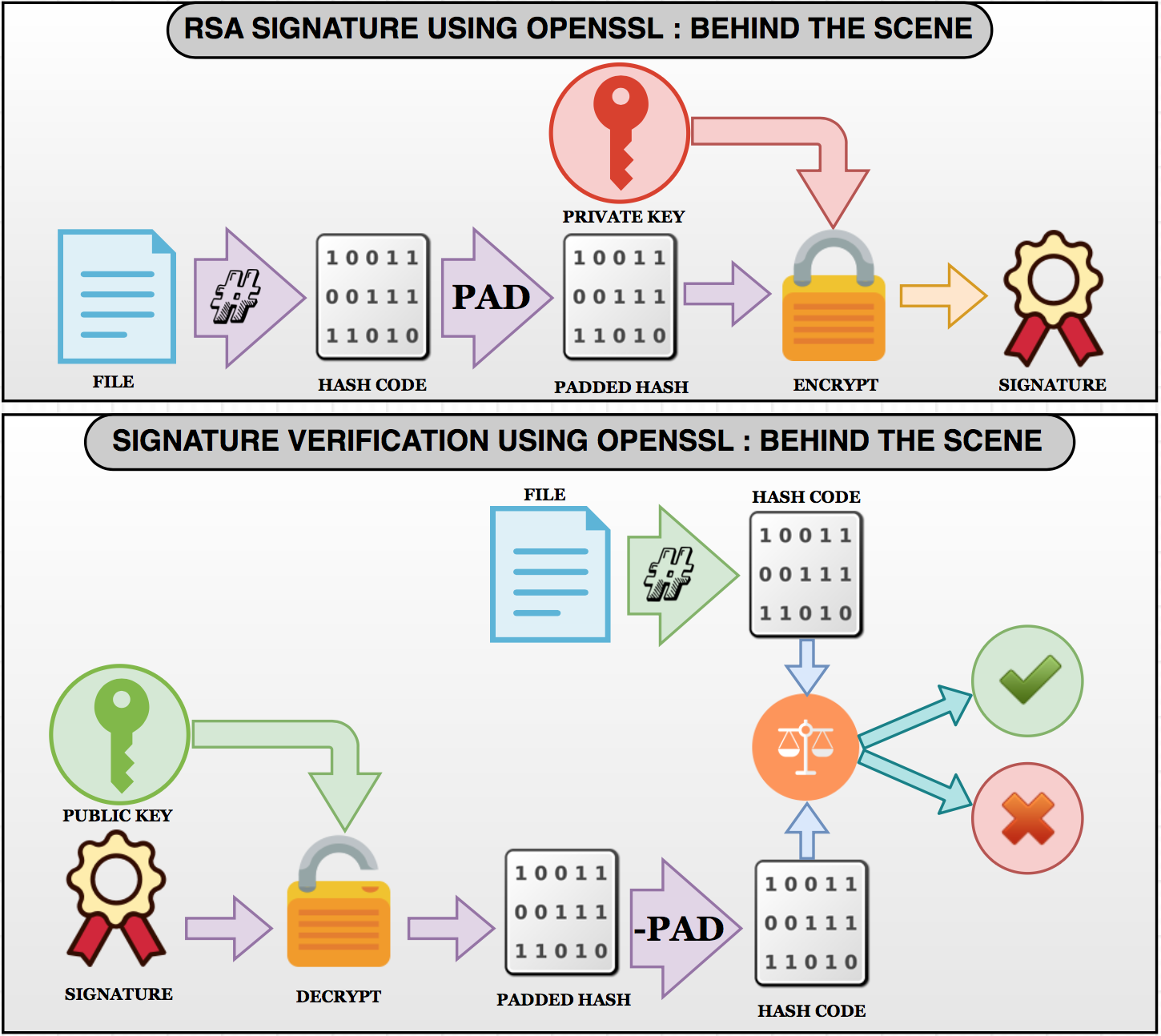
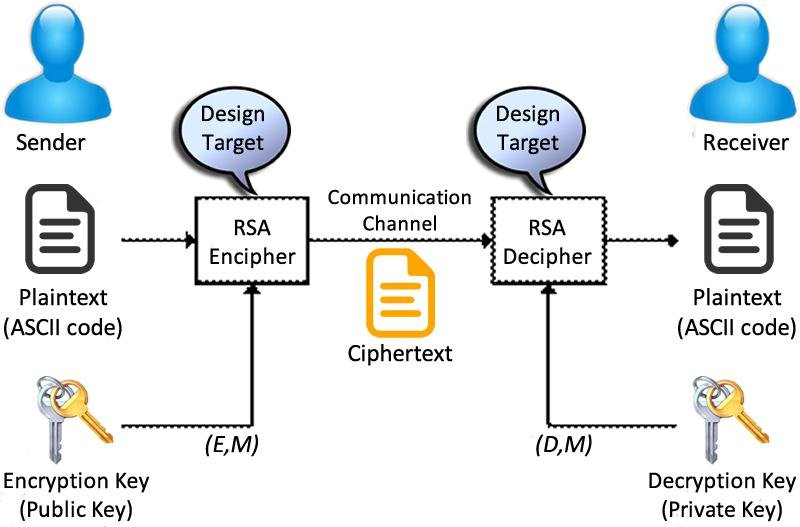
RSA演算法

- RSA加密步驟

1. 請對方公布他的公鑰

2. 將你的訊息使用他的公鑰加密

3. 將加密後的訊息公布或傳給他

4. 他接到訊息後，以他的私鑰解密

- 當然，若他要回傳訊息給你，你就要公布自己的公鑰給他

RSA演算法

Step 1. 請對方公布他的公鑰

先請對方隨機選擇兩個不同的質數\(p, q\)，然後計算\(N = pq\)。

再來計算 \(R = φ(N) = φ(p)φ(q) = (p - 1)(q - 1)\)。

最後任意找一小於\(R\)且與\(R\)互質的數\(e\)，計算其在模\(R\)下的逆元\(d\)。

Note：\(N\)與\(e\)就是他的公鑰，\(d\)就是他的私鑰

RSA演算法

Step 2. 將你的訊息使用他的公鑰加密

假設你要傳給他的訊息經過編碼後變成數字\(n\)

計算 \(c = n^e \bmod N\) 給他。

Note：\(N\)與\(e\)就是他的公鑰，\(d\)就是他的私鑰

因為質因數分解沒有已知的多項式時間演算法，所以若沒有私鑰\(d\)，是無法有效率地僅由\(c, N, e\)解出\(n\)的

RSA演算法

Step 3. 將加密後的訊息公布或傳給他

就... 傳啊

RSA演算法

Step 4. 他接到訊息後，以他的私鑰解密

計算 \(c^d \bmod N\)，就可以得到\(n\)了。

Note：\(N\)與\(e\)是他的公鑰，\(d\)是他的私鑰，\(c\)是密文，\(n\)是明文

證明如下：(有興趣自己看)

\(c^d = n^{ed} = n^{1+hφ(N)} = n ( n^{φ(N)})^h\equiv n(1)^h\equiv n \ (\bmod N)\)

休息一下

好累喔 QQ

迪菲-赫爾曼密鑰交換

相較於RSA演算法而言，迪菲-赫爾曼密鑰交換是一個比較好懂且執行速度較快的金鑰交換方式。

(不過它無法用來傳訊)

它是基於離散對數問題無法在多項式時間內解決的事實，來達到金鑰交換的目的。

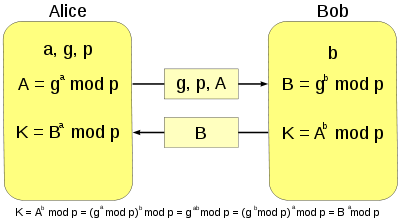
迪菲-赫爾曼密鑰交換

D-H密鑰交換中，有許多要用到次方的地方，以下演算法可以在多項式時間內計算出\(g^x \bmod m\)：

1. 先遞迴計算\(a \equiv g^{⌊\frac{x}{2}⌋} \pmod m\)
2. 如果\(x\)是偶數，則\(g^x \equiv a^2 \pmod m\)
3. 如果\(x\)是奇數，則\(g^x \equiv a^2g \pmod m\)

反問題則無有效率的解，才得以保證加密安全

假設\(g^x = a \pmod m\)，現在給定\(a, g, m\)三數，求\(x\)。

- D-H密鑰交換步驟

1. 雙方先決定自己的私鑰

2. 任一方公布公鑰

3. 雙方將公私鑰混和交給對方

4. 雙方分別解密，解出共同密鑰

- 因為D-H密鑰交換無法進行傳訊，所以必須使用解出的金鑰進行對稱式加密傳訊。

迪菲-赫爾曼密鑰交換

雙方都先各決定一個任意數字，不需要讓任何人知道。假設我的是\(x\)，他的是\(y\)。

Step 1. 雙方先決定自己的私鑰

Note：\(x\)是我的私鑰，\(y\)是他的私鑰

迪菲-赫爾曼密鑰交換

公布兩個數\(g, m\)，滿足\(g\)是整數模\(m\)乘法群下的原根

Step 2. 任一方公布公鑰

Note：\(x\)是我的私鑰，\(y\)是他的私鑰，\(g, m\)是公鑰

也就是說：

若\(d\)是滿足\(g^d \equiv 1 \pmod m\)的最小正整數，那麼\(d = φ(m)\)

迪菲-赫爾曼密鑰交換

兩人分別計算 \(X = g^x \bmod m\) 和 \(Y = g^y \bmod m\) 並將此兩數公布出去。

Step 3. 雙方將公私鑰混和交給對方

Note：\(x\)是我的私鑰，\(y\)是他的私鑰，\(g, m\)是公鑰，\(X, Y\)是公開訊息

迪菲-赫爾曼密鑰交換

我拿到\(Y\)之後將其取\(x\)次方，得到 \(Y^x = g^{xy} \bmod m\)

他拿到\(X\)之後將其取\(y\)次方，得到 \(X^y = g^{xy} \bmod m\)

Step 4. 雙方分別解密，解出共同密鑰

Note：\(x\)是我的私鑰，\(y\)是他的私鑰，\(g, m\)是公鑰，\(X, Y\)是公開訊息

迪菲-赫爾曼密鑰交換

因為雙方都同時知道這個\(g^{xy} \bmod m\)，而且不會被任何人知道，所以可以安心用這個數字做為對稱式加密傳訊的金鑰

休息一下

好累喔 QQ

橢圓曲線加密

了解橢圓曲線加密之前，要先知道什麼是橢圓曲線。

橢圓曲線是形如 \(y^2 = x^3 + ax + b\) 的方程式的圖形，

長的大概像這樣：

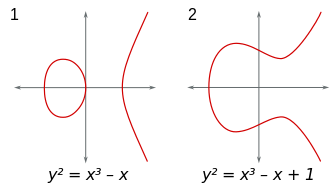
橢圓曲線加密

橢圓曲線上的點集合可以與一種加法運算構成一個交換群，現在就來定義這個運算。

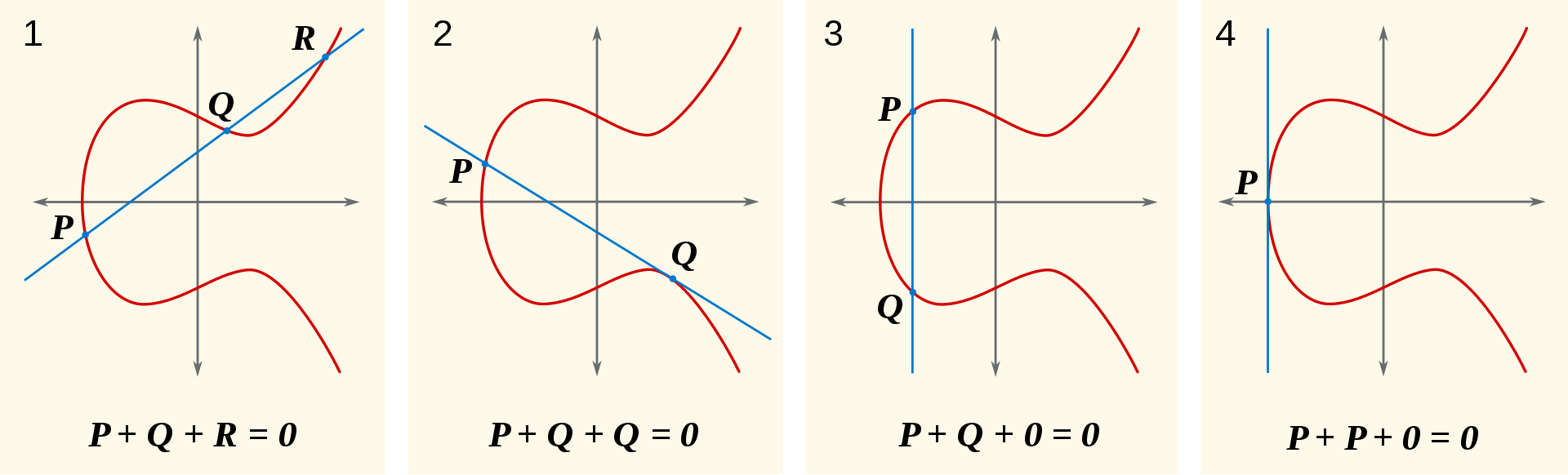
加法

\(P+Q = -R\)

二倍

\(2Q = -P\)

逆元

\(Q = -P\)

單位元

\(0\)：無窮遠點

橢圓曲線加密

不過真正在實作加密的時候，所用的橢圓曲線只包含滿足方程式的格子點(\(x, y\) 坐標都是整數的點)，而且這些坐標值一定皆在\(0\)~\(p-1\)的範圍內。

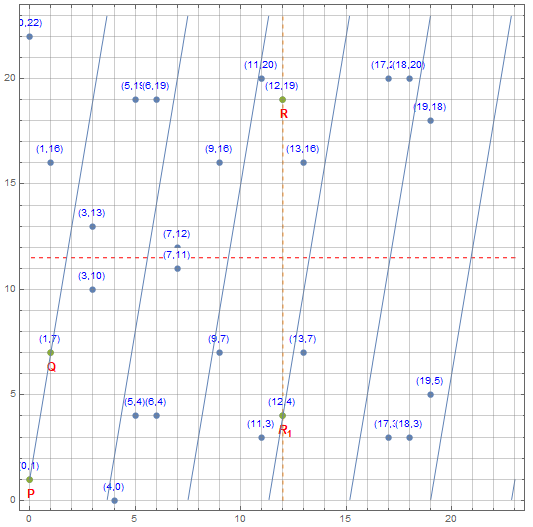
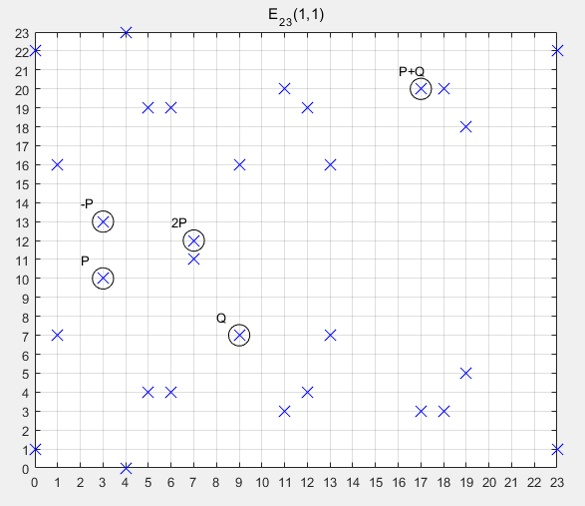
橢圓曲線加密

正式地說：有限域上的橢圓曲線是滿足

\(y^2 \equiv x^3 + ax + b \pmod p\)

的所有格子點構成的集合。

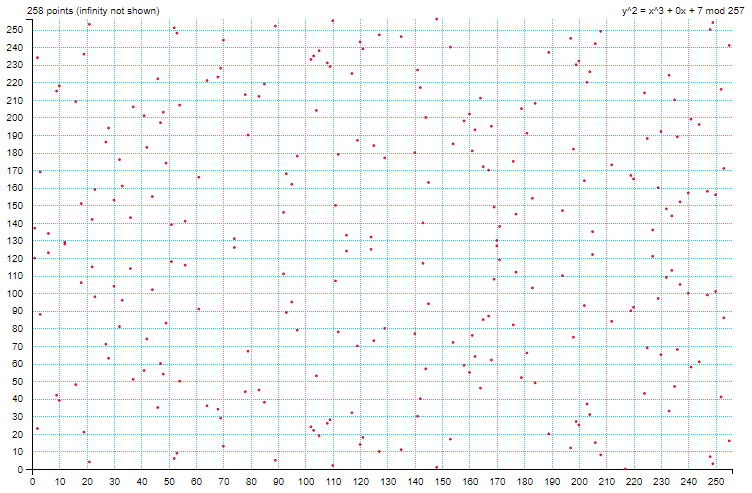
橢圓曲線加密

若有限域上的橢圓曲線上兩點\(P(x_p, y_p)\)與\(Q(x_q, y_q)\)，那麼定義\(P + Q = R(x_r, y_r)\)

\(x_r = ( \lambda^2 - x_p - x_q) \bmod p\)

\(y_r = ( \lambda^2 - \lambda x_r - y_p) \bmod p\)

其中\( \lambda\)是過\(P, Q\)兩點的連線斜率\(m \bmod p\)

若\(P, Q\)共點，則斜率\(m\)定義為\( (3ax^2_ p)/2y_p\)

橢圓曲線加密

複習得啦

橢圓曲線
元素	曲線上的點
加法	共線三點的和是單位元素
單位元素	無窮遠點
反元素	對稱點
運算律	交換律、結合律

\(y^2 \equiv x^3 + ax + b \pmod p\)

- 橢圓曲線加密步驟

1. 雙方約定一組公鑰

2. 選定一個私鑰，將公鑰加密傳給對方

3. 對方也選定一個私鑰，將訊息加密回傳

4. 解密，解出共同密鑰

- 橢圓曲線加密的公鑰比較特殊，可以從網路上查詢比較適用的金鑰當作公鑰

橢圓曲線加密

上網搜尋了一組橢圓曲線與一個已經公布的起始點\(G\)。

橢圓曲線加密

Step 1. 雙方約定一組公鑰

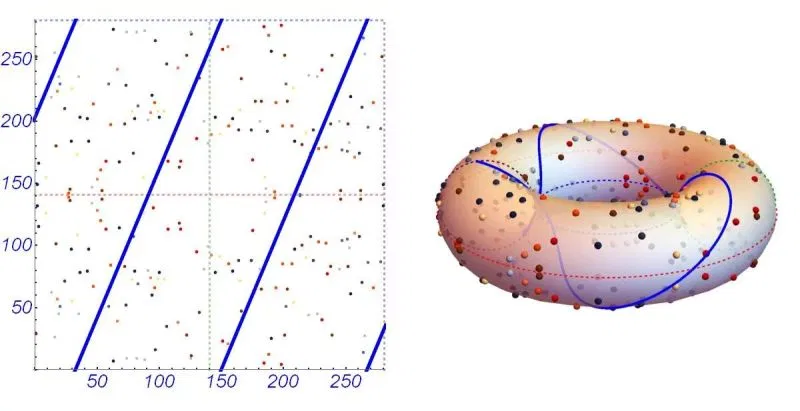
橢圓曲線加密

腦中先想出了一個數\(k\)當作私鑰，以便解密用，然後將 \(K = kG\) 這個點的坐標傳給對方。

Step 2. 選定一個私鑰，將公鑰加密傳給對方

Note：\(k\)是我的私鑰，\(kG\)是公開資訊

要求心裡也想了一個數\(r\)

將兩個點\(rG\)與\(M + rK\)傳回來

橢圓曲線加密

Step 3. 對方也選定一個私鑰，將訊息加密回傳

其他人就只能看到\(G, K, rG, M + rK\) 四個點的交換，根本解不出\(k\)跟\(r\)，更別提解出\(M\)了。

Note：\(k\)是我的私鑰，\(r\)是他的私鑰

將\(M + rK\)減去\(k\)倍的\(rG\)，就得到共同訊息\(M\)了

橢圓曲線加密

Step 4. 解密，解出共同密鑰

Note：\(k\)是我的私鑰，\(r\)是他的私鑰，\(G, K, rG, M + rK\)是公開資訊

橢圓曲線加密

顯然，這方法能成立，是因為就算擁有\(rG\)與\(G\)，還是無法算出\(r\)的確切值，

因為這個有限域橢圓曲線上的運算是無法做除法運算的，才因此有了這個加密方法。

顯然，這個\(G\)必須是要經過挑選的，他的倍數要能到曲線上所有的點上才行，不然就會產生有效率的破解方法。

幸好網路上已經公布了許多能用的曲線以及對應的\(G\)點，直接拿來用就行了。

資訊世界的

防偽與防盜

6 身分驗證

怎麼證明是本人？

身分驗證

如何確認資料是否被篡改？

身分驗證

數位簽章

公開金鑰 + 數位簽章

數位簽章

- 數位簽章

* 加密、解密金鑰不同

* 公鑰：用於解密，相當於驗證簽名

* 私鑰：用於加密，相當於生成簽名

數位簽章

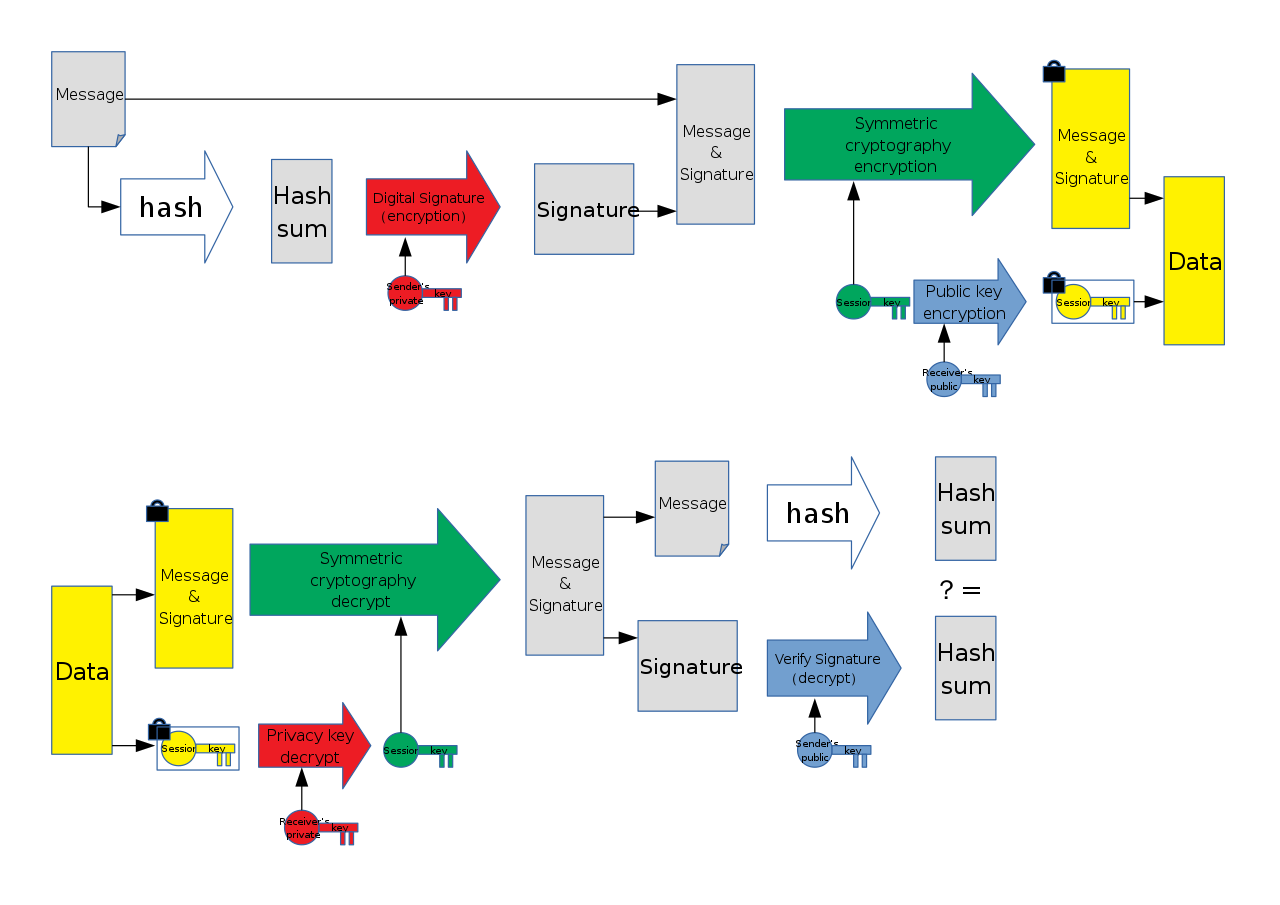
數位簽章：使用私鑰

雜湊

非對稱加密：使用公鑰

對稱加密

數位簽章

簽章驗證：使用公鑰

雜湊

非對稱解密：使用私鑰

對稱解密

哪裡怪怪的

- 數位簽章

* 加密、解密金鑰不同

* 公鑰：用於解密，相當於驗證簽名

* 私鑰：用於加密，相當於生成簽名

我要怎麼信任你的公鑰？？？

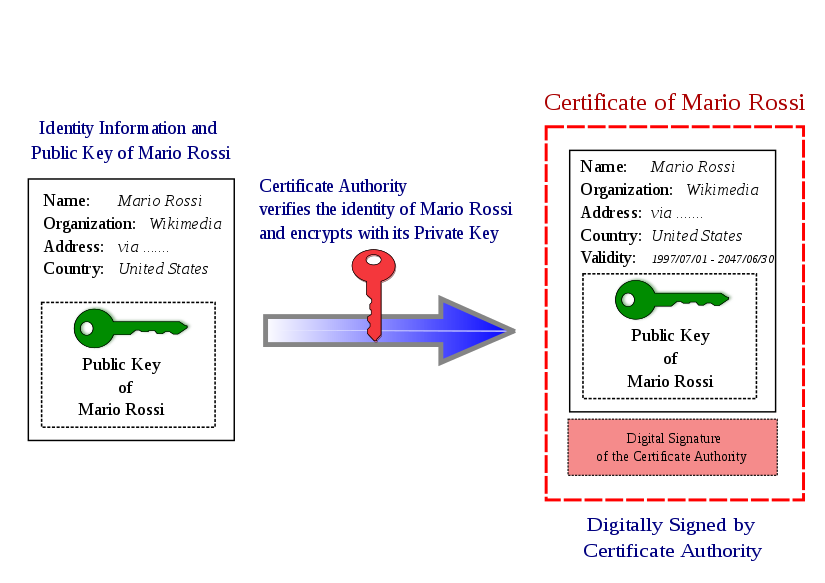
數位憑證

公鑰交給認證機構

私鑰自己保留

數位憑證

- 數位簽章

* 加密、解密金鑰不同

* 公鑰：用於解密，經過信任的憑證機構認證後，人人皆可取用

* 私鑰：用於加密，自行保留

取得公鑰的方法：

利用憑證機構的公鑰驗證數位簽章

量子物理學

將何去何從

7 量子電腦

量子位元

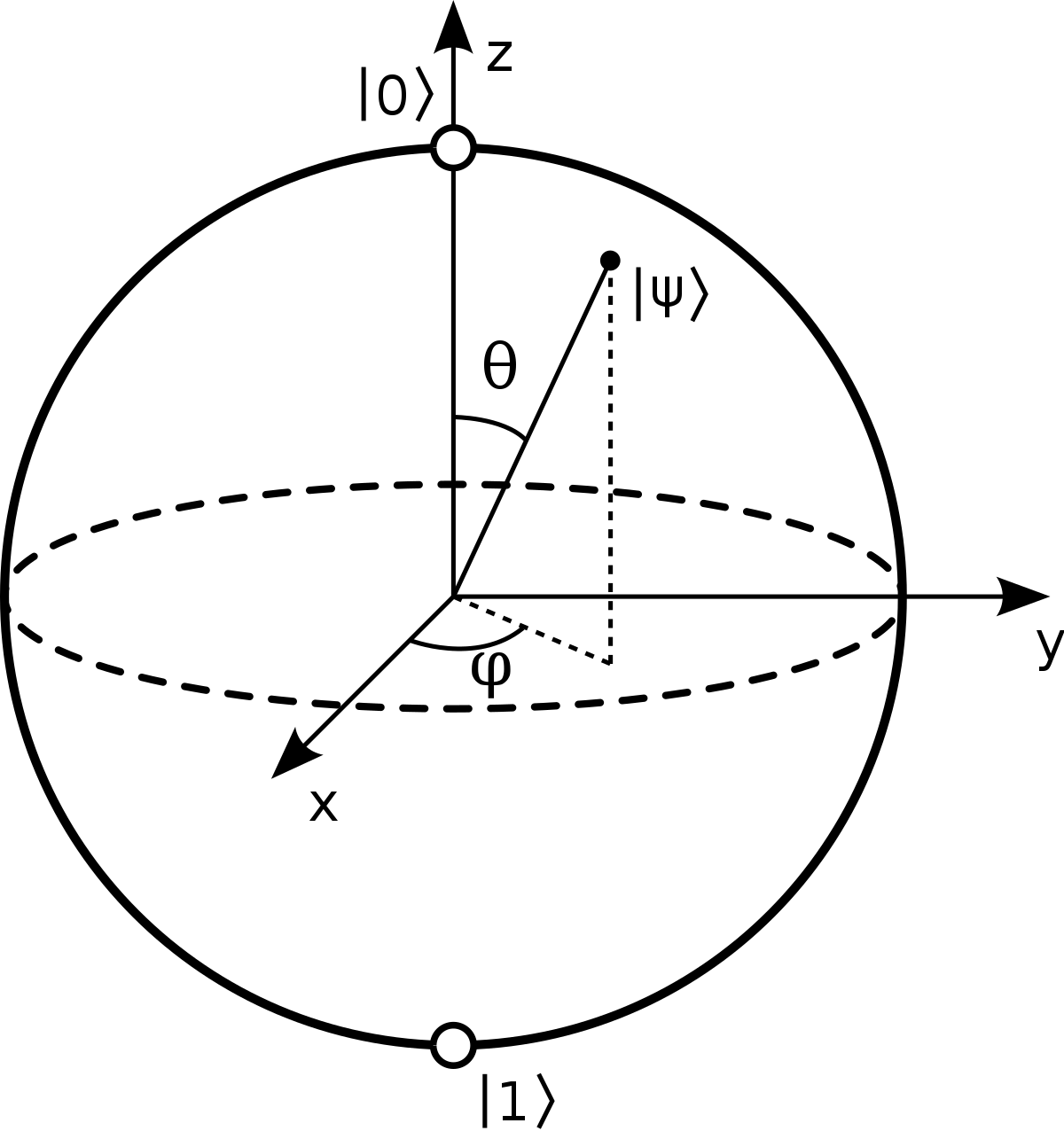
可以同時是0又是1的東東

\(|\psi \rangle =\alpha |0\rangle +\beta |1\rangle ;\quad \alpha ,\beta \in {\mathbb {C}}\)

量子邏輯閘

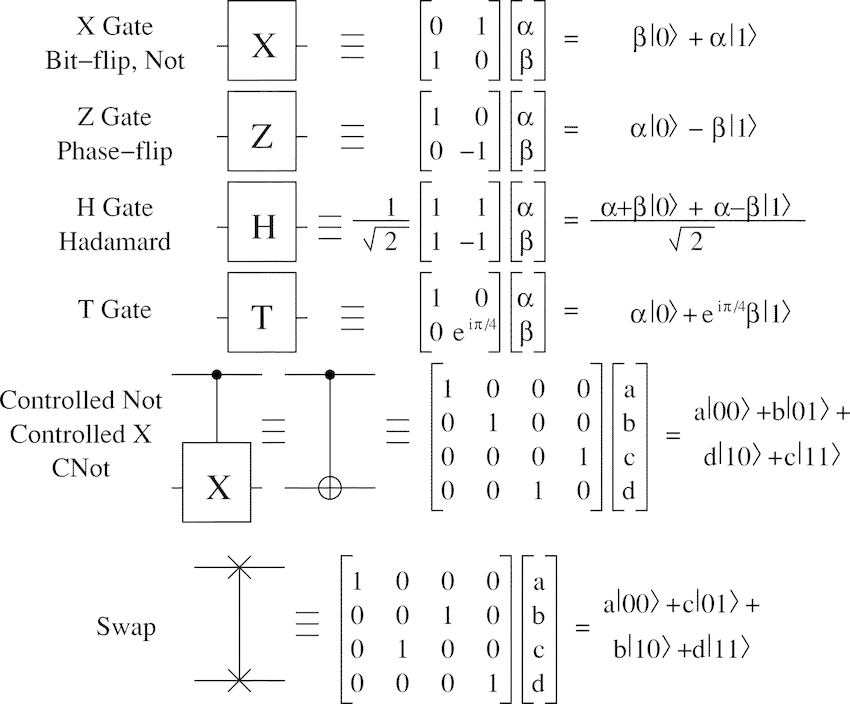
量子演算法

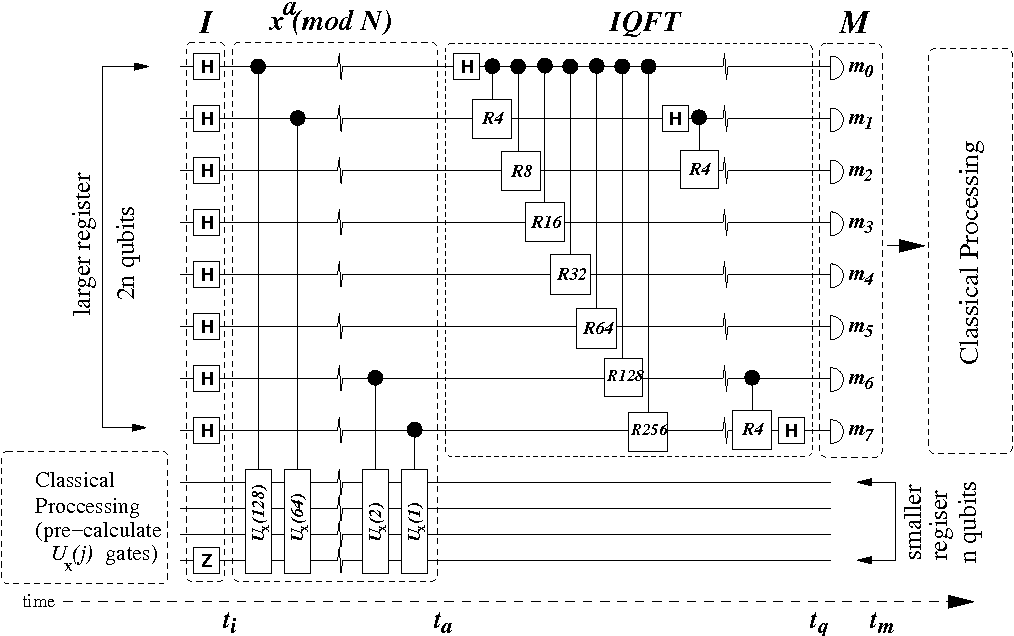
RSA加密

Shor's Algorithm

RSA的理論基礎是來自質因數分解的困難度，如果有人找到了一個快速分解大整數的算法，那RSA可能就無法保證安全性了。

還記得RSA嗎？

量子密鑰分發

量子密碼有以其人之道還制其人之身的概念。

量子位元的物理特性可以破解現代密碼系統，那麼也可以用量子位元的物理特性作為防範。

- 古典通道：傳送古典訊息(0或1)的通道

- 量子通道：傳送量子位元的通道

兩種通道都有被竊聽的危險

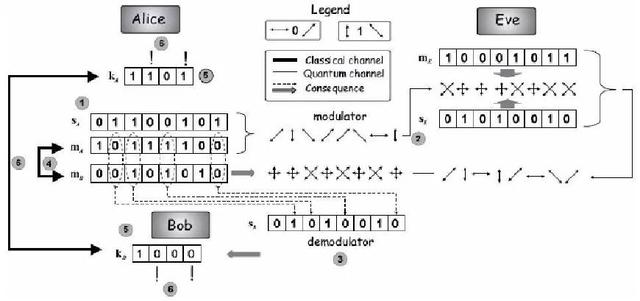
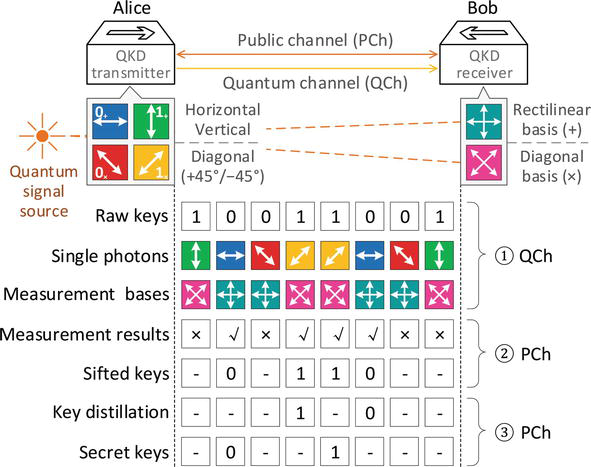
BB84協定

欲傳送訊息 (可能是密鑰)

BB84協定

隨機選定基底

BB84協定

接收方也隨機選定基底

BB84協定

利用古典通道檢查哪些基底正確配對

BB84協定

將訊息一半交換驗證，另一半作為共同訊息

E91協定

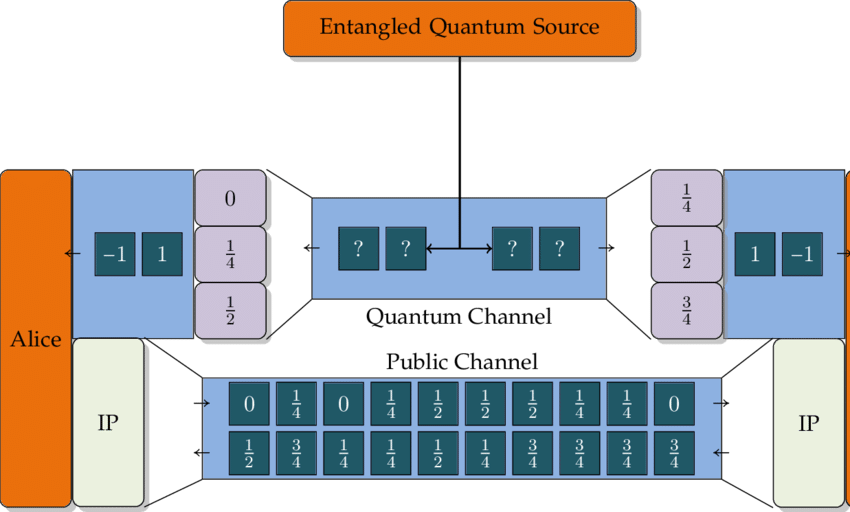
E91協定

外源纏結量子對

量子纏結現象：

當一對量子纏結起來時，它們的量子態是100%相反的

E91協定

各自在三個基底選擇一個測量

E91協定

雙方公開所用基底，若基底相同，可作為共同密鑰

大功告成！

感謝聆聽或睡著

~~或中暑~~

本著作係採用創用 CC 姓名標示-非商業性-相同方式分享 4.0 國際授權條款授權.