String Algorithms
-- 程式競賽進階篇 --
Warm up
什麼?! 你說老師沒教過字串!
Warm up
Terminologies
字串 (string):一串東西 一個數列也可以算是廣義的字串
字元 (character):字串裡面的每個元素都是字元
字母 (alphabet):所有可能會在字串出現的東西的集合
子字串 (substring):某字串內一段連續的字元
子序列 (subsequence):照某原字串順序排序的一些字元
前綴/後綴 (prefix/sufix):某字串的前幾個/後幾個字元
lexicographical order
定義字串\(S\)的字典序小於字串\(T\),若且唯若
\(S\)是\(T\)的前綴
或
存在一個位置\(k\)使得\(S_k \leq T_k\),且對於所有的\(i \leq k\)都有\(S_i = T_i\)
當然,首先要先定義字元的大小關係
lexicographical order
簡單來說就是從前面開始比較
遇到第一個不同的就看哪個字元比較小
Examples:
abc < acb
ac < acc
std::string
STL裡面也有提供一個可以儲存字串的資料結構
此外 因為資料結構不外乎陣列
所以std::string本質上是一個以字元作為元素的vector特化
所以vector能用的東西它幾乎都能用(?)
std::string
#include<iostream>
#include<string>
using namespace std;
signed main() {
string s;
cin >> s;
cin.getline(s, 10, 'a');
getline(cin, s);
}std::string
#include<iostream>
#include<string>
using namespace std;
signed main() {
string s = "this is a string";
cout << s.back() << s.front() << s[10] << endl;
char *str = s.c_str();
string t = s.substr(5, 10);
cout << s.length() << ' ' << s.size() << endl;
s.clear();
cout << s.empty() << endl;
s.push_back('a');
for(auto i: s) cout << i;
}std::string
#include<iostream>
#include<string>
using namespace std;
signed main() {
string s = "this", t = "that";
cout << (s == "this") << endl;
cout << (s < t) << endl;
s = s + t + s + 'a';
string n_str = "1001";
int n_int = stoi(n_str);
// stol, stoll, stoul, stod, stof ...
int x_int = 96;
string x_str = to_string(x_int);
}Practice
string matching
字串匹配是一個十分經典的問題
現在有一個字串\(S\)與另一個字串\(P\),問\(S\)有幾個子字串是\(P\)
它的做法也非常多
這邊會介紹五個
naive solution
#include<bits/stdc++.h>
using namespace std;
signed main() {
string s, p;
int cnt = 0;
cin >> s >> p;
for(int i=0;i<=s.size()-p.size();i++) {
int match = 1;
for(int j=0;j<p.size();j++) {
if(s[i+j] != p[j]) match = 0;
}
if(match) cnt++;
}
cout << cnt << endl;
}string::find

#include<bits/stdc++.h>
using namespace std;
signed main() {
string s, t;
cin >> s; cin >> t;
int match = 0, cnt = 0;
do {
match = s.find(t, match + 1), cnt++;
} while(match != string::npos);
cout << cnt << endl;
}string::find
#include<bits/stdc++.h>
using namespace std;
signed main() {
string s, p;
for(int j=0;j<=100;j++) {
for(int i=0;i<=99999;i++) s += 'a';
s += 'b';
}
for(int i=0;i<=100000;i++) s += 'a';
for(int i=0;i<=100000;i++) p += 'a';
cout << s.find(p) << endl;
}雖然大部分時間很快 但有的測資就會故意卡
string::find
#include<bits/stdc++.h>
using namespace std;
signed main() {
string s, p;
for(int j=0;j<=100;j++) {
for(int i=0;i<=99999;i++) s += 'a';
s += 'b';
}
for(int i=0;i<=100000;i++) s += 'a';
for(int i=0;i<=100000;i++) p += 'a';
cout << s.rfind(p) << endl;
}有時候他故意卡 你還是想唬爛 你可以用 string::rfind()
Robin-Karp Algorithm
曾經有人說過:只要是字串題,沒有hash解決不了的
一個hash不夠,就兩個。
其實好好處理hash的話
就可以不用會KMP或Z (?)
hashing
STL其實有hash可以用
unordered_map之類的東東好像是使用這種東西吧
#include<bits/stdc++.h>
using namespace std;
signed main() {
string s = "this", p = "that";
int h = hash<string>{}(s);
int g = hash<string>{}(p);
cout << h << ' ' << g << endl;
}hashing
hash是個神奇的東西
它的精神就是用一個數字來表示原字串
所以一旦hash完 就可以\(O(1)\)比對兩字串是否相等
事實上若搭配二分搜
你可以\(O(\log |S+T|)\)知道兩個字串的字典序大小關係
hashing
不過你可能覺得很沒用 因為hash一次就要\(O(|S|)\)
所以若要讓hash發揮威力
必須要在重複使用hash value的時機使用
字串匹配就是一個重複使用的例子
polynomial hashing
為了達到重複使用的目的,我們定義一個比較好計算的雜湊方式:
\(H(S) = (S_0 P^{n-1} + S_1 P^{n-2} + ... + s_{n-1}P^0) \bmod M\)
具體code長這樣:
const long long P = 131, M = 998244353;
long long hash(string s) {
long long val = 0;
for(auto i: s) {
val *= P, val += i, val %= M;
}
return val;
}polynomial hashing
這樣定義的好處是:
假設我們已經存好字串\(S\)所有前綴的hash value
long long val[maxn + 5];
const long long P = 131, M = 998244353;
void poly_hash(string s) {
for(int i=0;i<s.size();i++) {
val[i] = (val[i] + s[i]) % M;
val[i+1] = (val[i] * P) % M;
}
}polynomial hashing
假設我們已經存好字串\(S\)所有前綴的hash value
那我們就可以\(O(1)\)查詢任意子字串的hash value!
long long val[maxn + 5];
const long long P = 131, M = 998244353;
void poly_hash(string s) { 略 }
long long substr_hash(int a, int b) { // 0-base (a, b]
return (val[b] - val[a]*modpow(P, b-a) + M) % M;
}
// modpow(P, b-a) 可以預處理polynomial hashing
回到字串匹配
你會發現你只是重複比對\(S\)的一堆子字串是否與\(P\)相同
signed main() {
string s, p;
cin >> s >> p;
poly_hash(s);
long long hashp = hash(p);
int cnt = 0;
for(int i=0;i<=s.size()-p.size();i++) {
if(subseq(i, i+p.size()) == hashp) cnt++;
}
cout << cnt << endl;
}Practice
Gusfield's Algorithm
-- hash一定有風險 請斟酌使用 --
這裡是另外一個可以在\(O(|S| + |P|)\)時間完成的確定性字串匹配演算法
很多時候它都被稱做 Z-algorithm
Z - Array
首先要介紹一個叫做Z-陣列的東東
它是一個與字串相同長度的陣列,每個原素\(Z[k]\)代表的是以位置\(k\)為始的最長子字串長度,使得這子字串是整個字串的前綴
以ACBACDACBACBACDA為例:

calculating Z-Array
計算Z-陣列的方法蠻麻煩的
這個演算法有一個隨著演算法進行變動的區間\(s[x...y]\)
這個區間是一個原字串的前綴,而且\(y\)盡量大
從左到右算,假設你現在要計算\(Z[i]\)
1. 假如\(Z[i]\)在區間\(s[x...y]\)外 -> 暴力掃
2. 假如\(Z[i]\)在區間內 -> \(Z[i]\)至少有\(\min(Z[i-x], y-i+1)\)
calculating Z-Array

calculating Z-Array
我沒有電繪板QQ
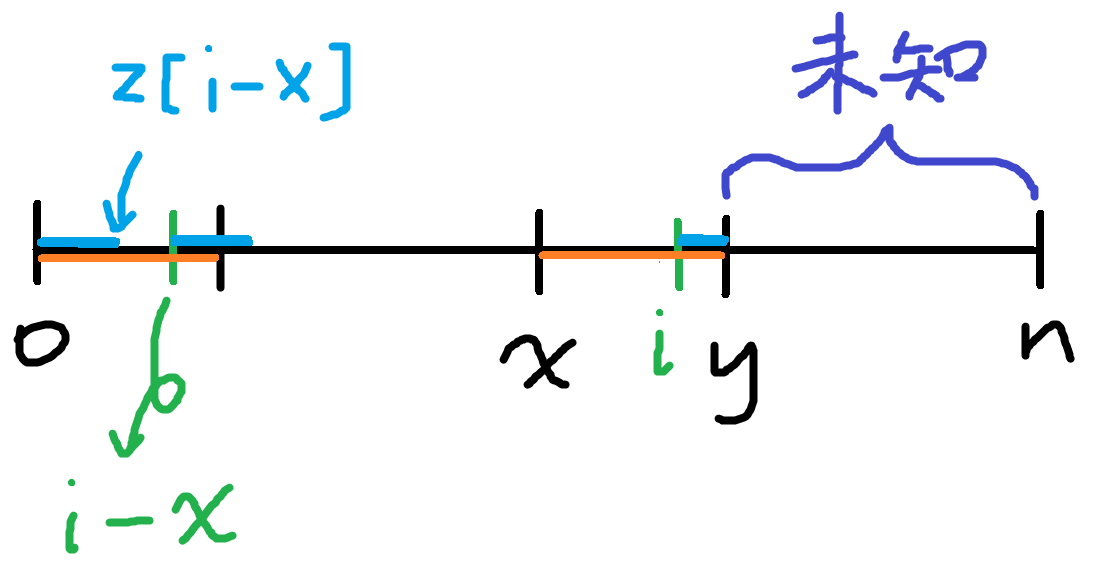
calculating Z-Array
vector <int > get_Z(string &s){
vector <int > Z(s.size());
int x = 0, y = 0;
for(int i = 0; i < s.size(); i++){
Z[i] = max(0, min(y-i+1, Z[i-x]));
while(i+Z[i] < s.size() && s[Z[i]] == s[i+Z[i]])
x = i, y = i+Z[i], Z[i]++;
}
return Z;
}calculating Z-Array
複雜度?
因為我們維護的區間是:目前能使\(y\)盡量大的原字串前綴
所以每次計算出一個新的\(Z[i]\)被算出來時,\(y\)值都只會加不會減
而\(y\)值最多是\(|S|\),所以總複雜度\(O(|S|)\)
Z-Array and
string matching
有了Z-陣列,字串匹配就變得異常輕鬆
假設你要在字串 "CDACBACBACDA" 找 "ACB"
就像這樣做一次Z-陣列
Knuth-Morris-Pratt Algorithm
KMP算法是另外一種字串匹配算法
我個人是覺得Z-Algorithm比較直觀
但是KMP有時還是可以斟酌使用
然後KMP跟MP差在哪
Morris-Pratt Algorithm
講KMP之前先講MP算法
一樣暴力做 只是失配的時候跳過去 (?)
MP算法定義了一個失配函數 (failure function)
基本上就是字串每個前綴的次長共同前後綴長度 (?)
Morris-Pratt Algorithm
基本上就是字串每個前綴的次長共同前後綴長度 (?)
signed main() {
string s = "ABCCBABABCB";
vector<int> Fail = build_failure(s);
for(auto i: Fail) cout << i << ' ';
}0 0 0 0 0 1 2 1 2 3 0 Morris-Pratt Algorithm
void KMPSearch(string t, string p){
vector <int> fail = build_failure(p);
int i = 0; // index for t[]
int j = 0; // index for p[]
while (i < t.size()){
if(p[j] == t[i]){ // match
j++, i++;
}
if(j == p.size()){ // found
printf("Found pattern at index %d \n", i-j);
j = fail[j-1];
}
else if(i < t.size() && p[j] != t[i]){ // mismatch
if(j != 0) j = fail[j-1];
else i++;
}
}
}Morris-Pratt Algorithm
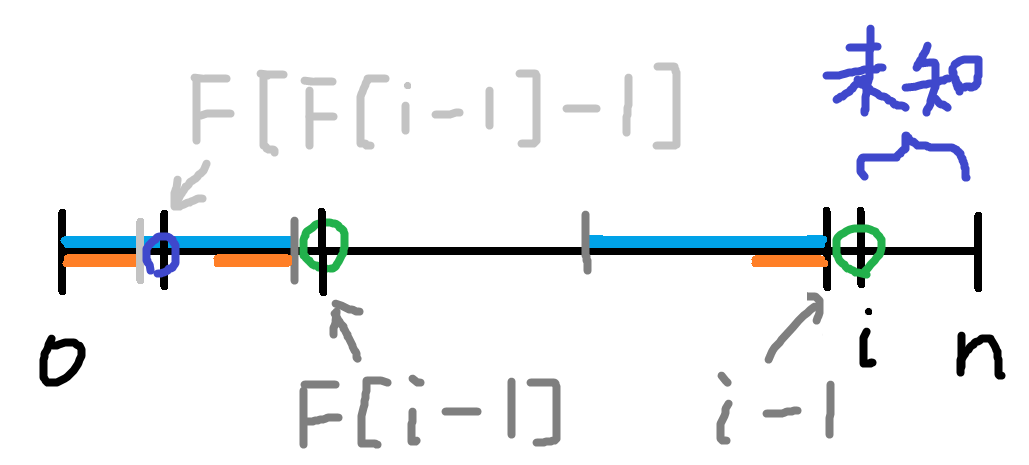
基本上就是字串每個前綴的次長共同前後綴長度
那我們要怎麼計算這個失配函數呢?
Morris-Pratt Algorithm
基本上就是字串每個前綴的次長共同前後綴長度
那我們要怎麼計算這個失配函數呢?
vector<int> build_failure(string &s) {
vector <int > fail = {0};
for(int i = 1, q = 0; i < s.size(); i++) {
// q = fail[i-1];
while(q && s[i] != s[q]) q = fail[q-1];
fail.push_back(q += (s[i] == s[q]));
//if(s[i] == s[q]) fail[i] = fail[q];
}
return fail;
}Practice
Furthermore
Aho-Corasick Automaton
字典樹 (Trie)
後綴數組 (suffix array) + LCP
好難我都不會 QQ
Next
-- 複雜度唬爛大法 --
平方分箱 與 根號算法