Logicke systemy 03
Motor zariadenia (výstup Y) sa môže uviesť do chodu, ak spínač S1 na riadiacom paneli (vstup A) je zopnutý a súčasne dverný spínač zariadenia (vstup B) je zopnutý a súčasne nadprúdová ochrana motora zariadenia (vstup C) je vypnutá.
Slovny zápis
Logicky výrok
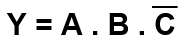
Pravdivostná tabuľka
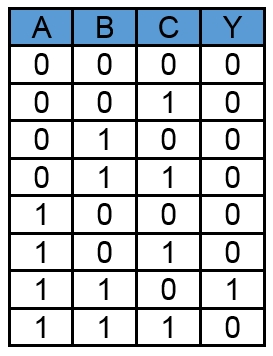
Pravdivostná tabuľka

Pravdivostná tabuľka zobrazuje všetky kombinácie vstupov A, B, C a stav výstupu Y.
Graficky
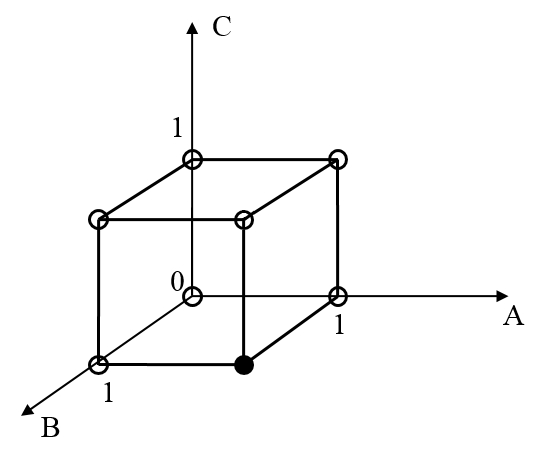
Graficky
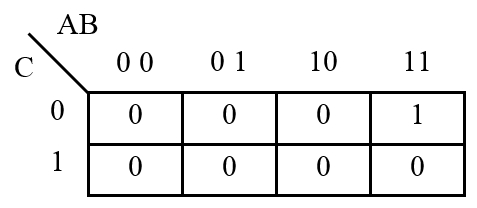
Karnaughová mapa zobrazuje všetky kombinácie vstupov v inej forme ako pravdivostná tabuľka. Používa sa hlavne pri grafickom spôsobe minimalizácie logickej funkcie.
Booleova algebra
Booleova algebra je vetvou matematiky pomenovanou podľa anglického logika a matematika Georga Boolea, ktorý ako prvý publikoval práce z tejto oblasti.
Booleova algebra nie je algebra čísel, s ktorou sa stretávame v matematike. Je to algebra logických stavov. Vzhľadom ku klasickej algebre je preto inak definovaná, napríklad v nej vôbec nenájdeme operácie odčítania a delenia (tieto funkcie v algebre stavov neexistujú).
Základne funkcie
Základné funkcie Booleovej algebry sú :
1. logický súčet OR
2. logický súčin AND
3. negácia NOT
Základné pravidlá
- A plus 0 je vždy A, ak je A=1 je to 1, ak je A=0 je to 0.
- A krát 0 je vždy 0.
- A plus 1 je vždy 1 bez ohľadu, akú logickú hodnotu má A.
- A krát 1 je vždy A, ak je A=1je to 1, ak A=0 je to 0…

Základné pravidlá
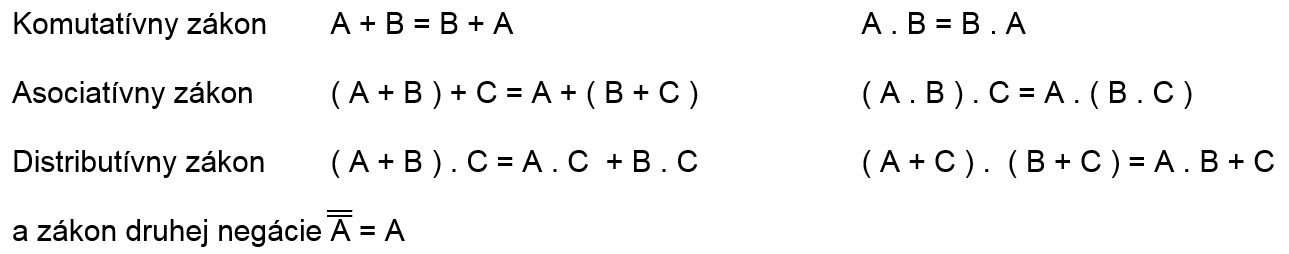
V Booleovej algebre pre logický súčet a logický súčin platia tieto zákony :
Dualita
Ľubovolnú logickú funkciu možno vyjadriť vhodným postupom aj v inom – duálnom tvare. O tejto vlastnosti pojednáva De Morganov zákon, ktorý hovorí že logickú funkciu NAND je možné vyjadriť v inom – duálnom tvare pomocou negácie a funkcie OR a opačne, logickú funkciu NOR je možné vyjadriť v inom – duálnom tvare pomocou negácie a logickej funkcie AND.
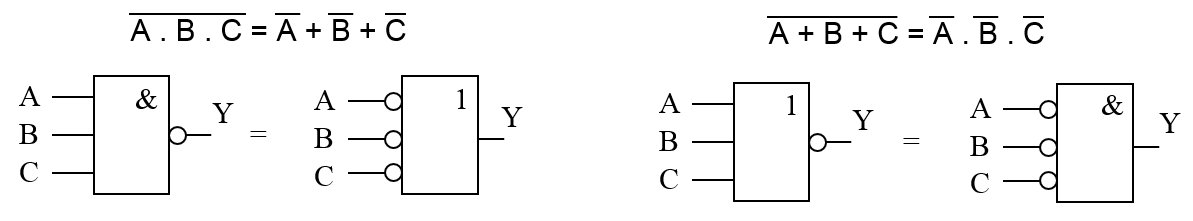
Shannov teorém
Shannov teorém zobecňuje De Morganov zákon a hovorí, že každá logická funkcia, ktorá obsahuje logické premenná A, B, C …, medzi ktorými sú operácie logického sčítania OR a logického násobenia AND sa dá napísať v inom – duálnom tvare ako funkcia, ktorá obsahuje pôvodné logické premenné A, B, C … , ale negované a logické operácie OR a AND sa medzi sebou vymenia.
Kanonický tvar tohoto teorému môžeme napísať ako :
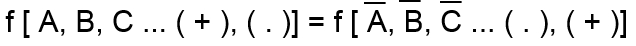
Príklad
Napríklad pre logický výraz ( A + C ) . ( B + C ) = Y môžeme podľa Shannovho teorému napísať :
s použitím základných pravidiel Booleovej algebry môžeme ďalej písať :
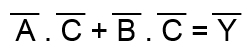
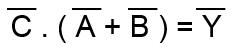
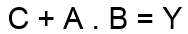
s použitím základných pravidiel Booleovej algebry môžeme ďalej písať :
ak na túto logický rovnicu aplikujeme Shannov teorém a s prihliadnutím na zákon druhej negácie, dostaneme :
s použitím základných pravidiel Booleovej algebry môžeme ďalej písať :
Minimalizácia logickej funkcie :
Zložité logické funkcie je možné minimalizovať – zjednodušiť niekoľkými metódami. Jednou z metód je použiť základné pravidlá Booleovej algebry. Napríklad pre logickú funkciu
je s použitím previdiel Booleovej algebry možné napísať
pričom podľa pravidiel boolovej algebry platí pre :
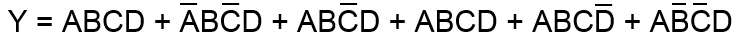
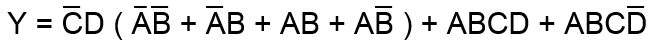
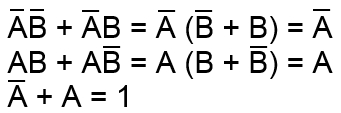

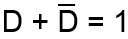
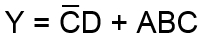
potom môžeme napísať
kde pre
potom môžeme napísať