Kim Lab journal club

the problem

  • EHR data are often available only at irregular intervals that vary among patients
  • machine learning algorithms cannot directly accommodate
  • "complete case" approach: biased, limited generalizability, few observations left
  • existing imputation methods: cross-sectional data (same time point)

MICE

multiple imputation:
multiple copies of a data set

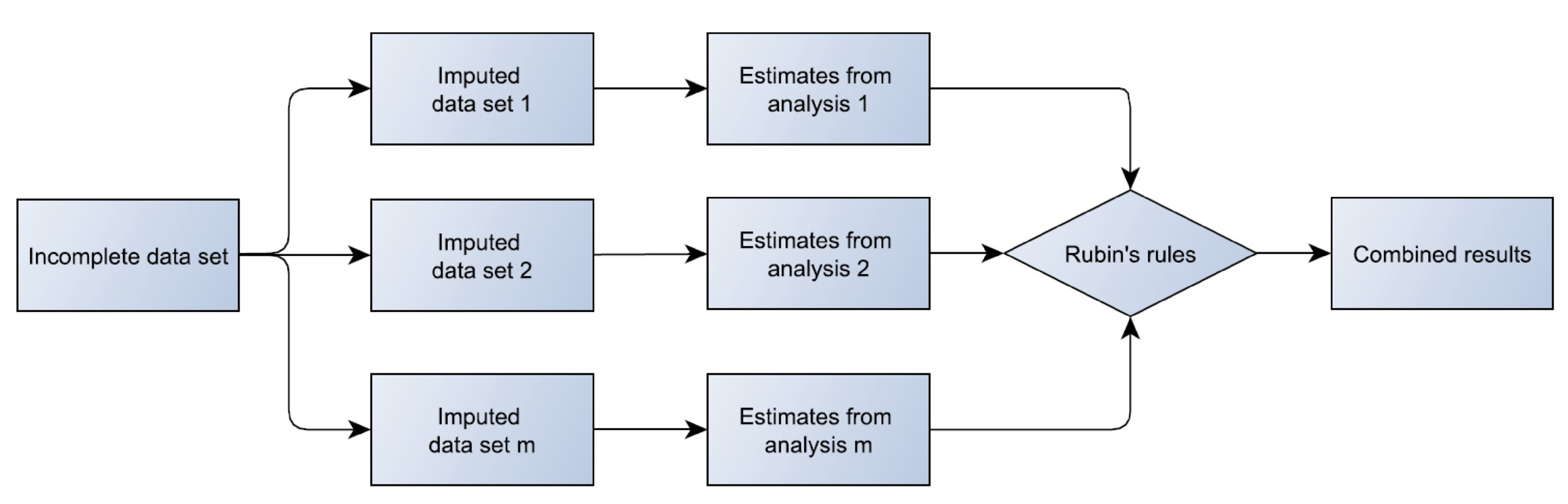
Multiple imputation by chained equations in praxis: Guidelines and review

Step 1: Naively impute missing data points of each variable (e.g., with mean value)

Step 2: Put NAs back in the age variable where it was missing.

Step 3: Train age on income and gender (linear regression) with available data

Step 4 Use the fitted model to predict the missing age values. 

Step 5: Repeat Steps 2–4 separately for each variable that has missing data, namely income and gender.

age, gender, income

for each cycle:

  • focus on one variable at a time
  • utilizes the correlation among the features

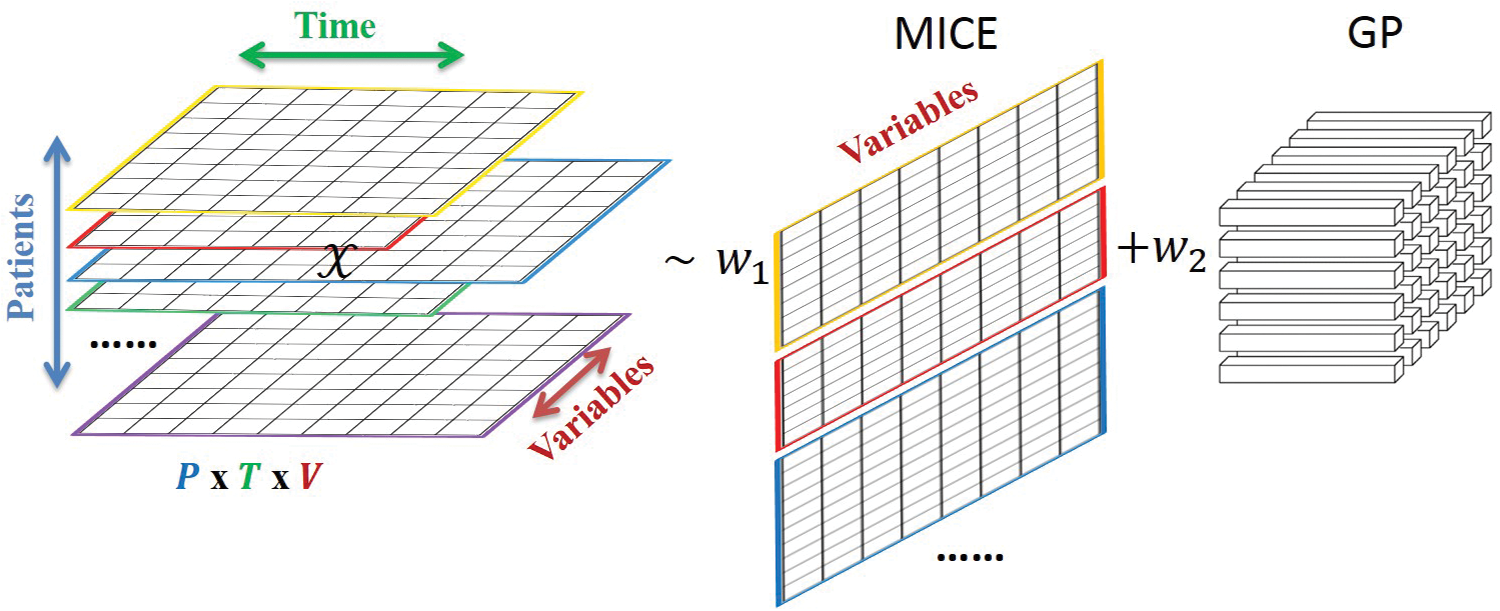
Gaussian processes

\(f(t_i)\) have a joint Gaussian distribution

P(f(t))

locality constraint

closer time points have more similar measurement values

cov(f(t_1), f(t_2)) = \alpha e^{-(t_1-t_2)^2/l}

Step 1: extract separate univariate time series for each patient and variable

Step 2: GPfit: MLE over \(\alpha\) and \(l\)

Step 3: infer values at unobserved time points

utilizes autocorrelation within each variable

dataset

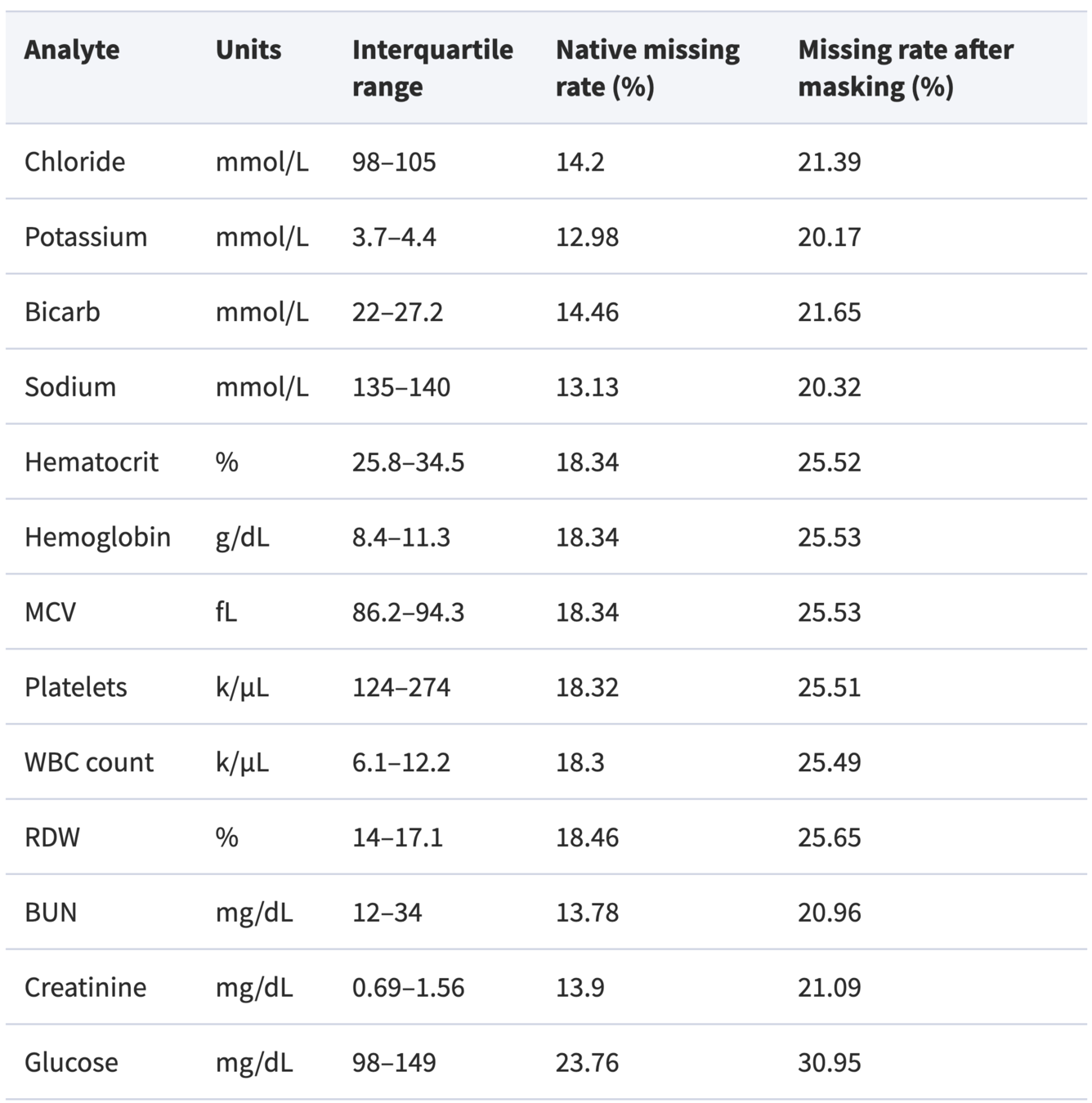
mask one result per analyte per patient

n_{GP}= [n_{MICE}\times \frac{\sigma_{MICE}}{\sigma_{GP}}] = [100 \times \frac{\sigma_{MICE}}{\sigma_{GP}}]

sampling

x_n = \frac{x-min(x)}{max(x) - min(x)}

normalization

nRMSD(a) = \sqrt{\frac{\sum{_{p,i}}I_{p,a,i}\left(\frac{X_{p,a,i} - Y_{p,a,i}}{max(Y_{p,a}) - min(Y_{p,a})}\right)^2}{\sum_{p,i}I_{p,a,i}}}

evaluation

patient \(p\)

analyte \(a\)

time index \(i\)

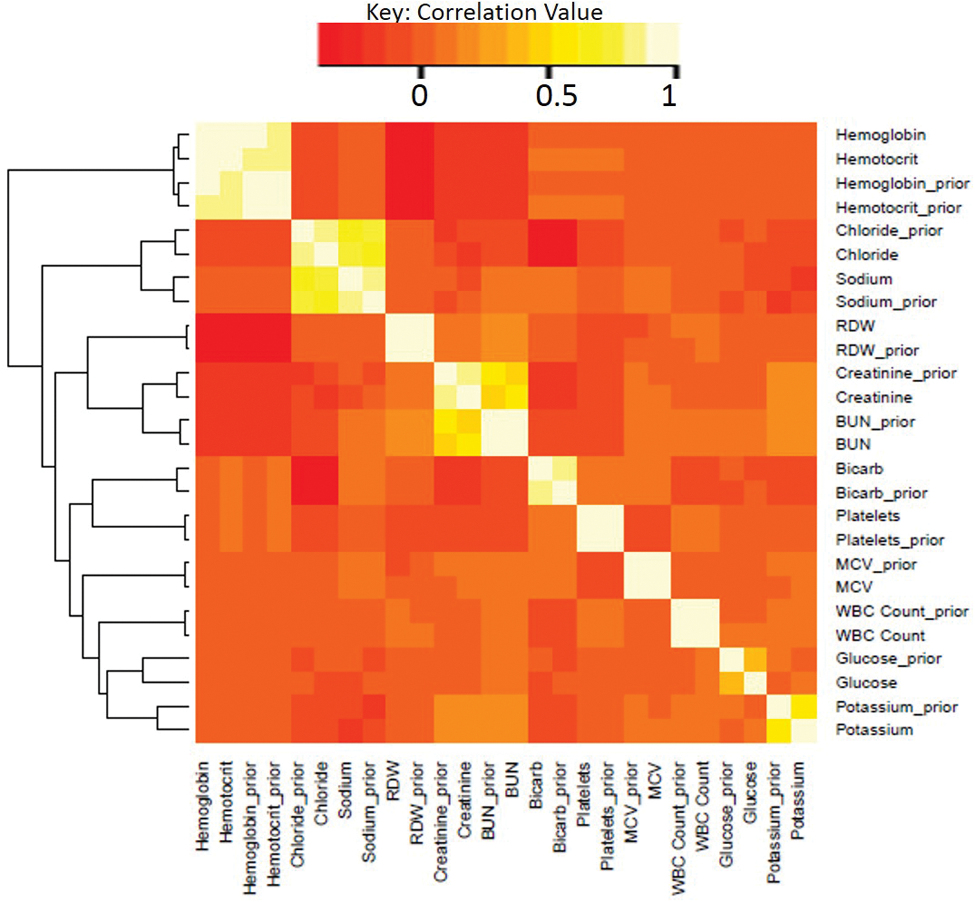
correlation between analytes and
between current and prior values for each analyte

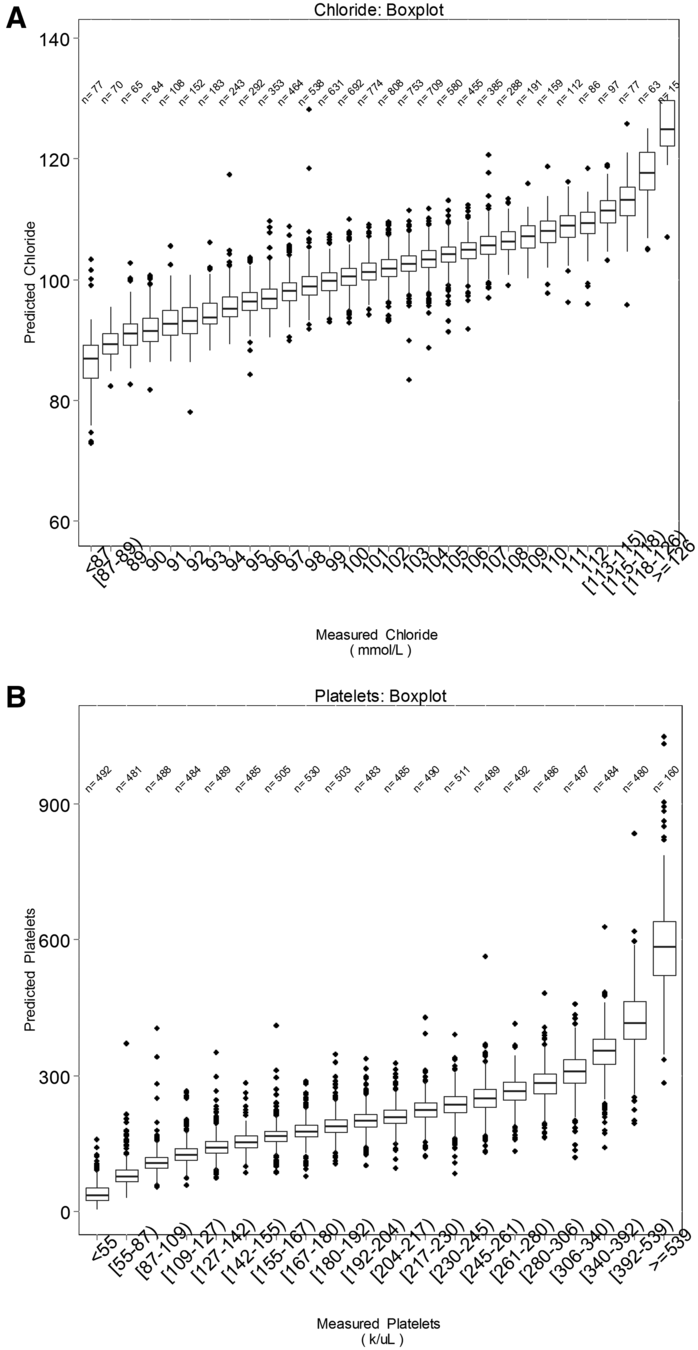
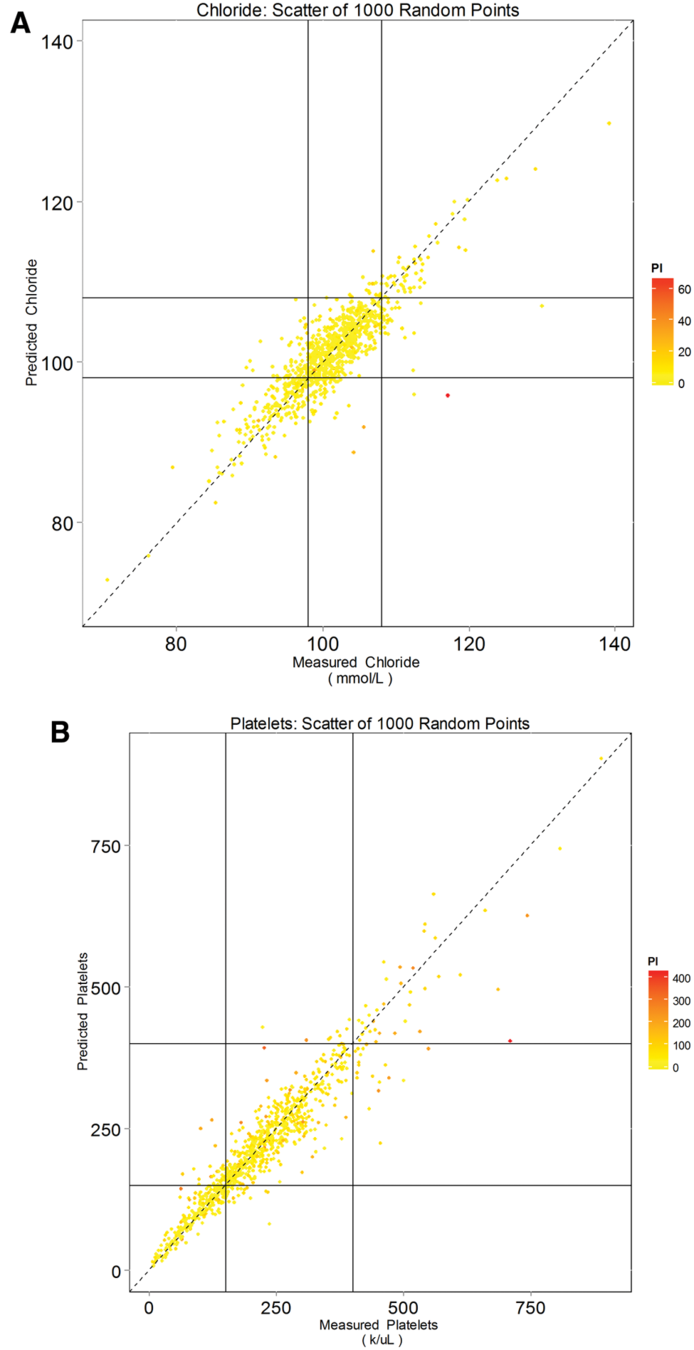
Other methods

  • Amelia II
  • https://www.ieee-ichi.org/2019/challenge.html

Limitations

  • > 2/3 patients were excluded
  • interpolations in place of GP for cases lacking sufficient temporal data to use 3D-MICE
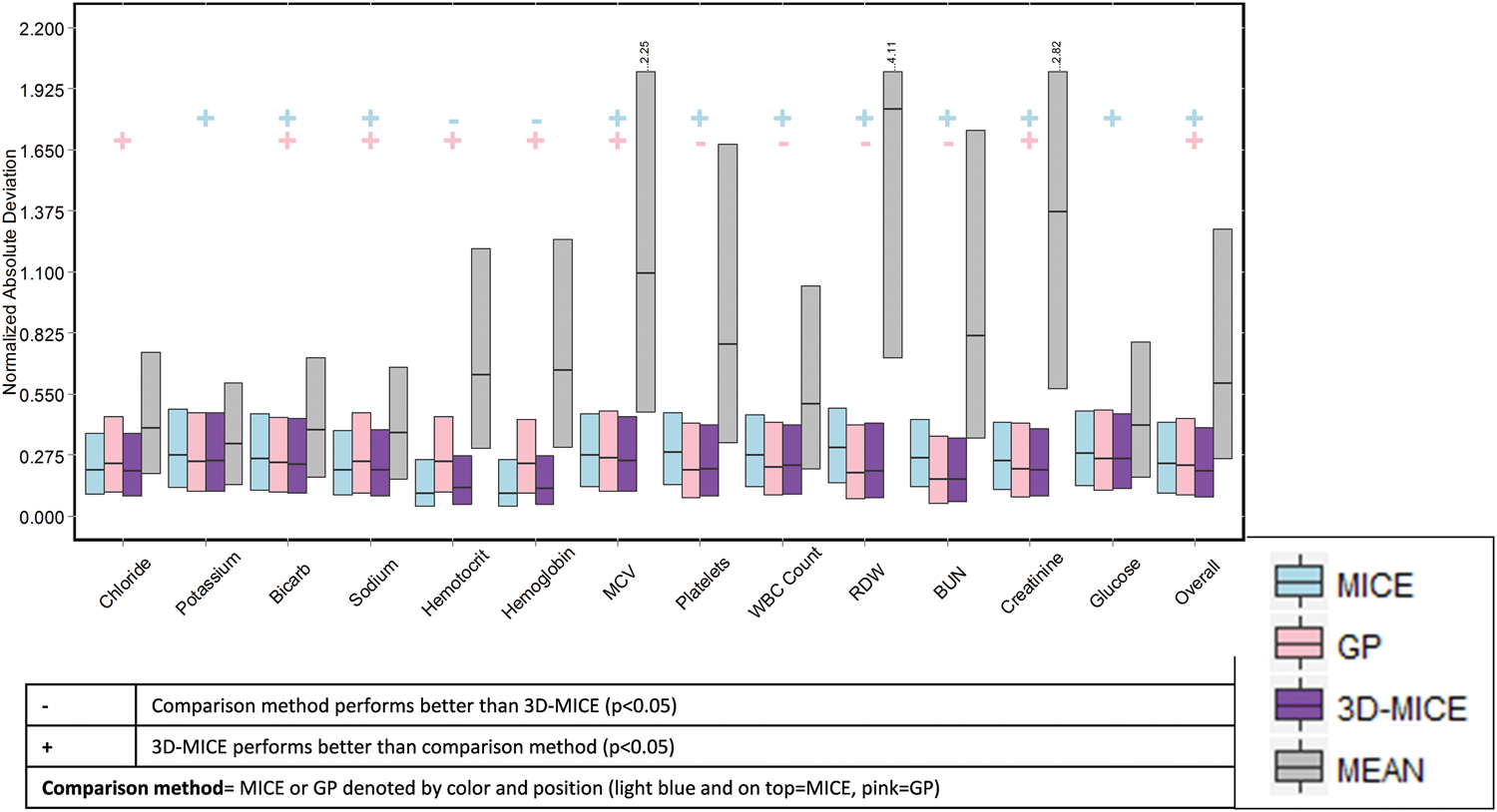
  • improvement over MICE or GP is small
  • missing at random assumption

Conclusion

  • 3DMICE is competitive in imputing missing data, especially when both inter-variable and within-variable  correlation are present
Made with Slides.com