Modern C

Chapter 4 — 5

Trang Le

2023-05-30

slides.com/trangdata/modernc-4-5/

Last time

  • C must be compiled to be executed
  • identifiers/names must be declared
  • objects must be defined
  • printf, puts
  • for, do, while
  • break, continue

  • switch

Chapter 4

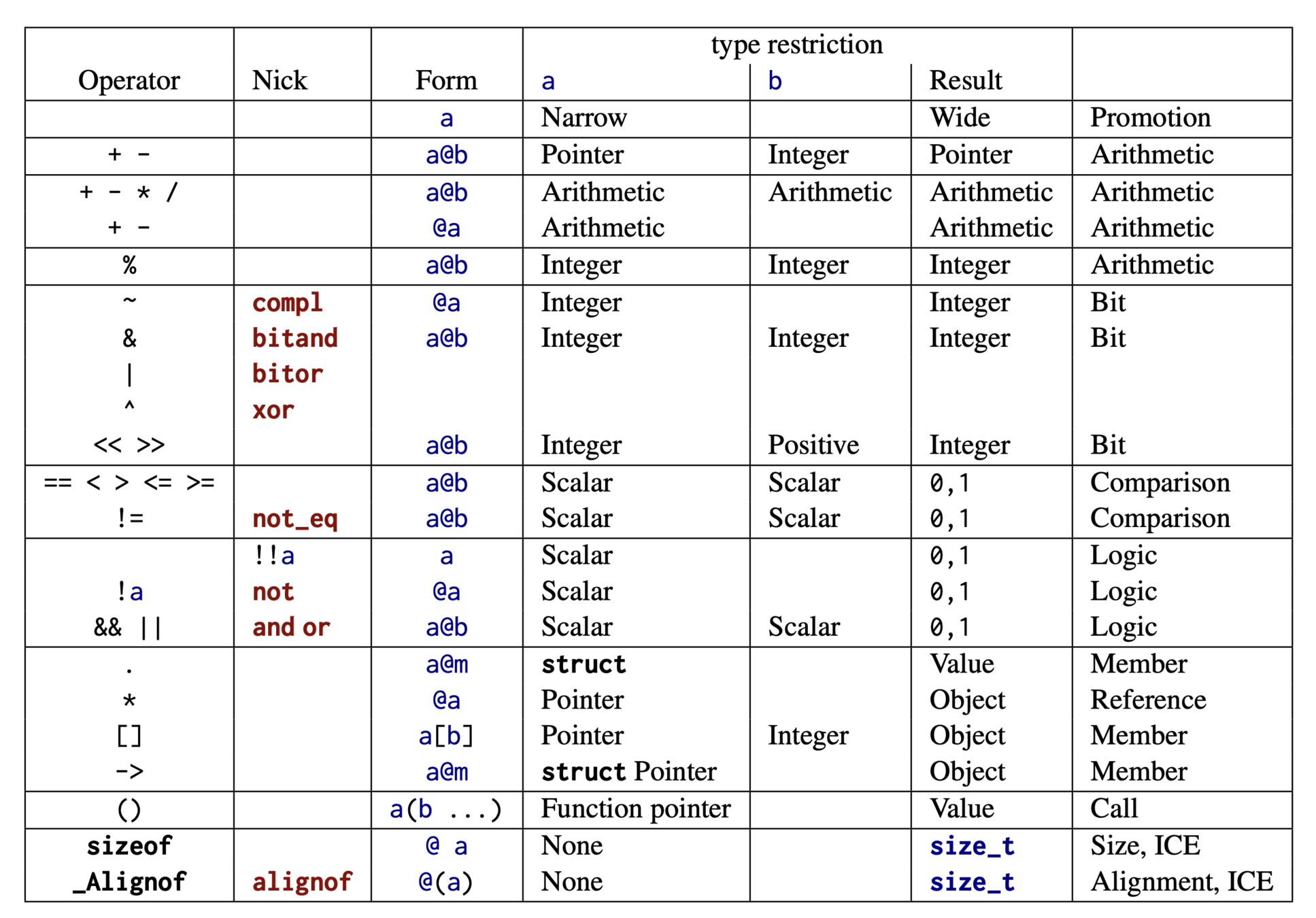
Expressing computations

  • arithmetic operators operate on values

  • assignment operators modify objects

  • comparison operators compare values

  • most operators evaluate their operands in a nonspecific order; except:
    &&, ||, and ?: impose an ordering on the evaluation of their operands

  • side effects are unpredictable

a + b

operator

operands

++i is equivalent to i += 1

--i is equivalent to i -= 1

Arithmetic on size_t implicitly does the computation %(SIZE_MAX+1).

The operations +, -, and * on size_t provide the mathematically correct result if it is representable as a size_t.

Unsigned arithmetic is always well defined.

Exs 8. Implement some computations using a 24-hour clock, such as 3 hours after 10:00 and 8 hours after 20:00.

3 hours after 10:00 is 13:00
8 hours after 20:00 is 04:00
12 hours after 05:00 is 17:00
2 hours after 23:00 is 01:00
#include <stdio.h>
#include <stdlib.h>

size_t clock_24(size_t a, size_t t) { return (a + t) % 24; }

int main(void) {
  size_t x[][2] = {
      {10, 3}, // 3 hours after 10:00
      {20, 8}, // 8 hours after 20:00
      {5, 12}, // 12 hours after 5:00
      {23, 2}, // 2 hours after 23:00
  };
  size_t nx = sizeof(x) / sizeof(x[0]);

  for (size_t i = 0; i < nx; i++) {
    printf("%zu hours after %02zu:00 is %02zu:00\n", x[i][1], x[i][0],
           clock_24(x[i][0], x[i][1]));
  }

  return EXIT_SUCCESS;
}

boolean

????????

conditional operator

 size_t size_min(size_t a, size_t b) { 
   return (a < b) ? a : b;
}

short-circuit evaluation

// This never divides by 0.
if (b != 0 && ((a/b) > 1)) {
  ++x; 
}
#include <tgmath.h>

#ifdef __STDC_NO_COMPLEX__
# error "we need complex arithmetic" 
#endif

double complex sqrt_real(double x) {
  return (x < 0) ? CMPLX(0, sqrt(-x)) : CMPLX(sqrt(x), 0);
}

&&, ||, ?:, and , evaluate their first operand first

Don’t use the , operator.

f(a)+g(b)

Don't depend on evaluation ordering.

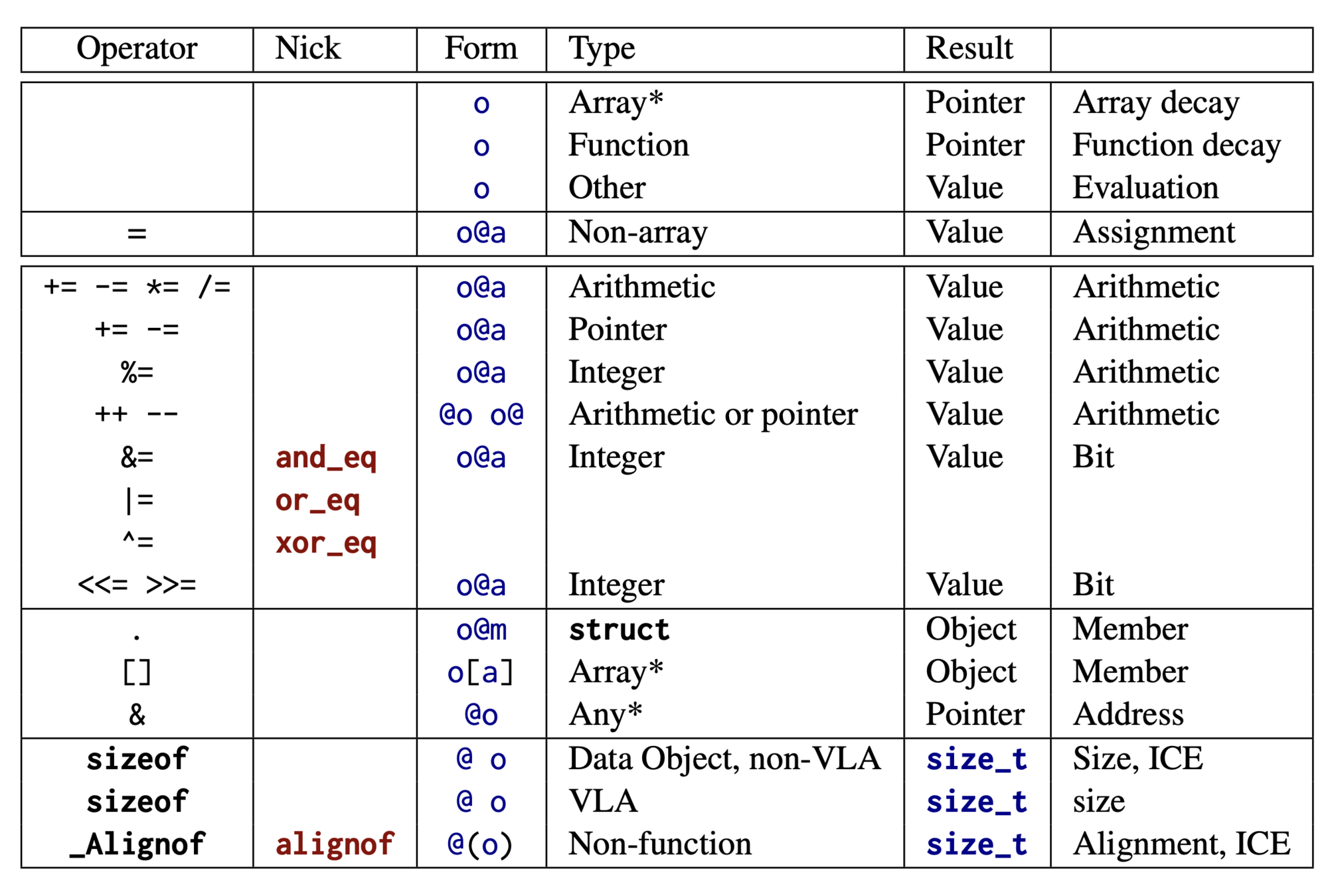
Chapter 5

Basic values and data

  • All basic C types are kinds of numbers, but some need promoting before doing arithmetic.

  • Values have a type and a binary representation.

  • When necessary, types of values are implicitly converted to fit the needs of particular places where they are used.

  • Variables must be explicitly initialized before their first use.

  • Integer computations give exact values as long as there is no overflow.

  • Floating-point computations only give approximated results that are cut off after a certain number of binary digits.

All values are numbers or translate to numbers.

All values have a type that is statically determined.

abstract state machine

x += 5;
/* Do something else without x in the meantime. */ 
x += 7;
/* Do something without x. */
x += 12;
x += 12;
/* Do something without x. */

or

optimization

Type determines optimization opportunities.

promoted to signed int

non-negative signed \(\subset\) unsigned

Use For
size_t sizes, cardinalities, or ordinal numbers
unsigned small quantities that can’t be negative
signed small quantities that bear a sign
ptrdiff_t large differences that bear a sign
double floating-point calculations
double complex complex calculations

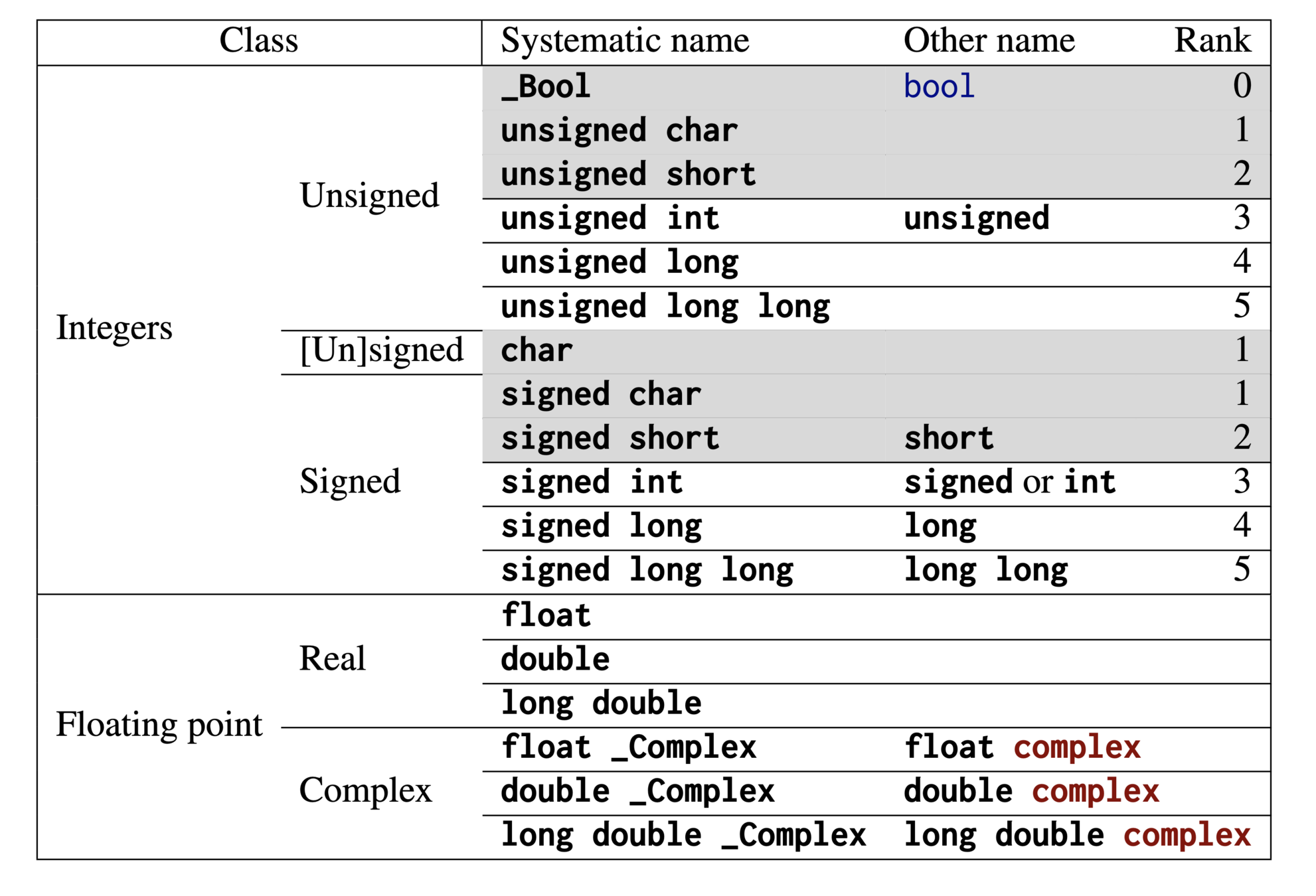
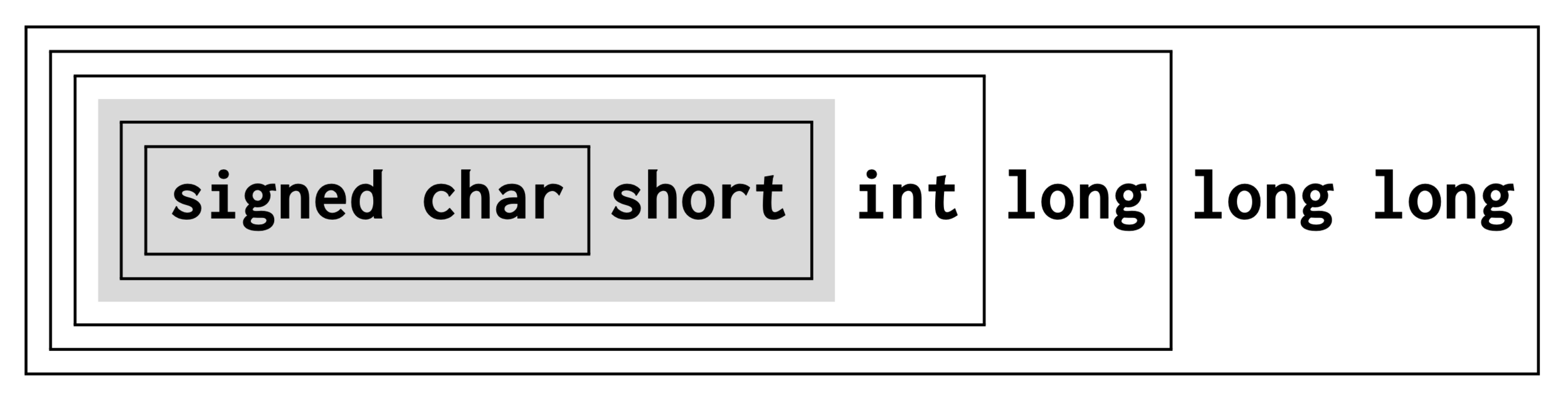
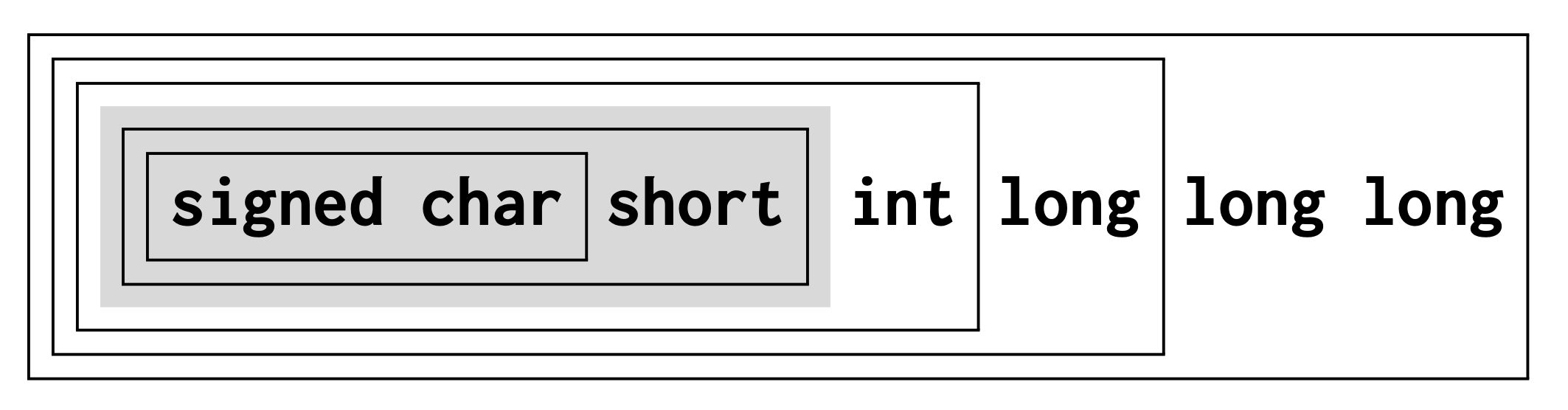
Decimal integer constants are signed. A decimal integer constant has the first of the three signed types that fits it.

Consider the constant 32768 on a platform:

  • minimal signed value: −32768
  • maximum value: 32767

doesn’t fit into signed ⇒ signed long
⇒ -32768 has type signed long

Exs 13. Show that if the minimal and maximal values for signed long long  have similar properties, the smallest integer value for the platform can’t be written as a combination of one literal with a minus sign.

maximum value is \(2^p-1\)
⇒ constant \(2^p\) doesn’t fit into signed long long

⇒ minimal signed value is \(-2^p\) cannot be written as a literal of the same type with a minus sign

Exs 14. Show that if the maximum unsigned is \(2^{16} -1\), then -0x8000 has value 32768, too.

0x8000 has value 32768

⇒ -0x8000 is UINT_MAX\( + 1 - 32768 = 2^{16} - 2^{15} = 2^{15} = 32768\)

For unsigned type:
UINT_MAX + 1 ≡ V + 1 ≡ 0 (mod UINT_MAX + 1)

Ex 17. Under the assumption that the maximum value for unsigned int is 0xFFFFFFFF (\(2^{32}-1\)), prove that -0x80000000 == 0x80000000 (\(2^{31}\)).

Similar argument applies here.

Exs 15. Show that the expressions -1U, -1UL, and -1ULL have the maximum values and type as the three non-promoted unsigned types, respectively.

Suppose maximum value for type unsigned is \(2^p-1\). Then,
-1U  ≡ \(2^p-1 \mod 2^p\), fits type

⇒ -1U has the maximum value for type unsigned

Literals have value, type, and binary representations.

Different types of constants generally lead to different values for the same literal.

double a = 1;			// Harmless; value fits type
signed short b = -1;		// Harmless; value fits type
signed int c = 0x80000000;	// Dangerous; value too big for type
signed int d = -0x80000000;	// Dangerous; value too big for type
signed int e = -2147483648; 	// Harmless; value fits type
unsigned short  g = 0x80000000; // Loses information; has value 0

signed int

−2147483648: minimal value

  2147483647: maximal value

Example

  • a pointer, type char const*const, is used to refer to strings

  • string literals are read-only

  • an object of const-qualified type is read-only.

string literals

enumerations

enum corvid { magpie , raven , jay , corvid_num , };
char const*const bird[corvid_num] = {
  [raven] = "raven", 
  [magpie] = "magpie", 
  [jay] = "jay",
};
...
for (unsigned i = 0; i < corvid_num; ++i)
printf("Corvid␣%u␣is␣the␣%s\n", i, bird[i]);

Enumeration constants are of type signed int.

Binary representation

\[\sum_{i = 0}^{p-1}b_i2^i\]

bit

precision

max: \(2^p -1\)

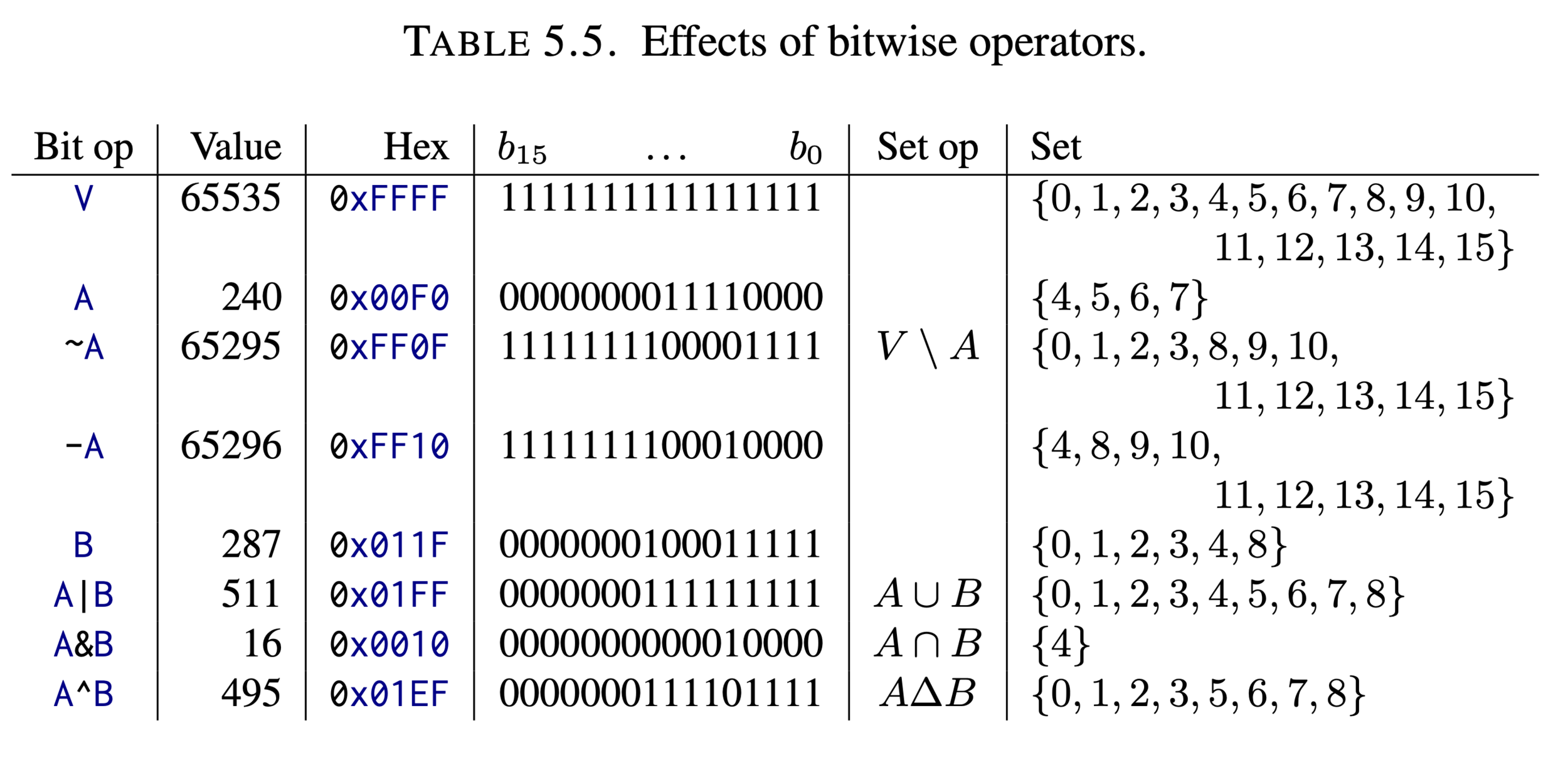
Exs 22. Show that A \ B can be computed by  A - (A&B).

\[RHS = \sum_{i = 0}^{p-1}a_i2^i - \sum_{i = 0}^{p-1}\bar{a}_i2^i= \sum_{i = 0}^{p-1}\hat{a}_i2^i\]

where \(a_i \in A, \bar{a}_i \in A \cap B \implies \hat{a}_i \in A \setminus (A \cap B) = A \setminus B\)

Exs 23. Show that V + 1 is 0.

\[V + 1 = 2^p - 1 + 1 = 2^p \equiv 0 \mod 2^p\]

Exs 24. Show that A^B is equivalent to (A - (A&B)) + (B - (A&B)) and A + B - 2*(A&B).

Exs 25. Show that A|B is equivalent to A + B - (A&B).

\[x \in A \Delta B \Longleftrightarrow x \in A\setminus B \cap B\setminus A \]

\[\implies A \wedge B = (A - (A\&B)) +  (B - (B\&A)) = A + B - 2*(A\&B)\]

\[A|B = A\&B + A\wedge B \]

\[= A\&B +A + B - 2*(A\&B) = A + B - A\&B \]

Exs 26. Show that ~B can be computed by V - B.

Exs 27. Show that -B = ~B + 1.

\[-B \equiv V +1 - B \equiv  \sim B + 1\]

Exs 22 \(\implies \) equivalent set op V \ B can be computed by

 V - (V&B) = V - B

Shift operators

A left-shift operation << corresponds to the multiplication 
by a power of two.

A right-shift operation >> corresponds to an integer division
by a power of two.

A = 240; \(A << 9 \equiv 240 \cdot 2^9 = 122880 = 57344 \mod 2^{16}\)

Exs 28. Show that the bits that are “lost” in an operation x>>n correspond to the remainder x % (1ULL << n).

\[x = \sum_{i = 0}^{p-1}b_i2^i = \sum_{i = 0}^{n-1}b_i2^i + \sum_{i = n}^{p-1}b_i2^i=2^n \cdot \left(\frac{1}{2^n}\sum_{i = 0}^{n-1}b_i2^{i} + \sum_{i = 0}^{p-n-1}b_i2^i\right)\]

bits lost
\(<2^n\)
remainder

\(x\) % (1ULL << \(n\)) = \(x \mod 2^n\)

number of times \(2^n\) fit in \(x\)

Commonly used on modern platforms is the two’s complement representation. It performs exactly the same arithmetic as we have seen for unsigned types, but the upper half of unsigned values (those with a high-order bit of 1) is interpreted as being negative.

bool is_negative(unsigned a) { 
  unsigned const int_max = UINT_MAX /2; 
  return a > int_max;
}

bool is_signed_less(unsigned a, unsigned b) {
  if (is_negative(b) && !is_negative(a)) return false;
  else return a < b; 
}

Floating-point data

s \cdot2^e \cdot\sum_{k=1}^{p}f_k2^{-k}

p, emin, emax: type dependent

Never compare floating-point values for equality.

Exs 35. Show that all representable floating-point values with \(e > p\) are multiples of \(2^{e−p}\).

s \cdot2^e \cdot\sum_{k=1}^{p}f_k2^{-k}
= s \cdot\sum_{k=1}^{p}f_k2^{e-k}
= s \cdot\sum_{k=1}^{p}f_k2^{e-p}2^{p-k}
= s \cdot2^{e-p} \cdot\sum_{i=0}^{p-1}f_{p-i}2^{i}

Exs 36. Print the results of the following expressions:
1.0E-13 + 1.0E-13 and
(1.0E-13 + (1.0E-13 + 1.0)) - 1.0

#include <stdio.h>

int main() {
  double s1 = 1.0E-13 + 1.0E-13;
  double s2 = (1.0E-13 + (1.0E-13 + 1.0)) - 1.0;
  printf("s1 = %.15lf\ns2 = %.15lf\n", s1, s2);

  return 0;
}
s1 = 0.000000000000200
s2 = 0.000000000000200

Exs 36. Print the results of the following expressions:
1.0E-13 + 1.0E-13 and
(1.0E-13 + (1.0E-13 + 1.0)) - 1.0

#include <stdio.h>

int main() {
  double s1 = 1.0E-13 + 1.0E-13;
  double s2 = (1.0E-13 + (1.0E-13 + 1.0E13)) - 1.0E13;
  printf("s1 = %.15lf\ns2 = %.15lf\n", s1, s2);

  return 0;
}
s1 = 0.000000000000200
s2 = 0.000000000000000

c-book-club/exercises/Session 2 at main · r-devel/c-book-club · GitHub

Made with Slides.com