Random walk, Markov chain and Brownian motion
Trang Le, PhD
2020-04-15
Guest lecture, Fundamentals of AI
Concepts
- Random walk
- Stochastic processes
- Markov chain
- Martingale
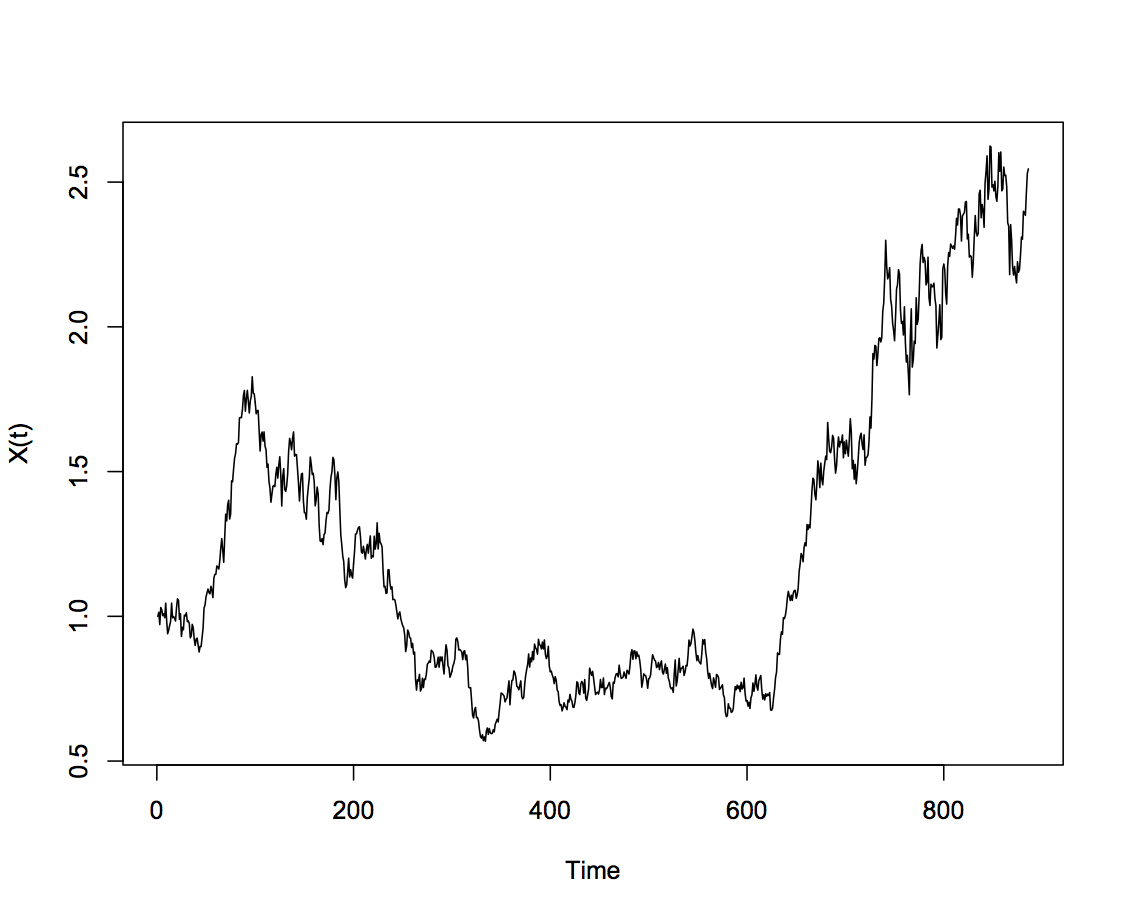
A stochastic process
is a collection of random variables indexed by time.
\(X_0, X_1, X_2, X_3, \cdots\) discrete time
\(\{X_t\}_{t\geq 0}\) continuous time
Alternatively, ...
a stochastic process is a probability distribution over a space of paths; this path often describes the evolution of some random value/system over time.
- Dependencies in a sequence of values?
- Long term behavior?
- Boundary events (if any)?
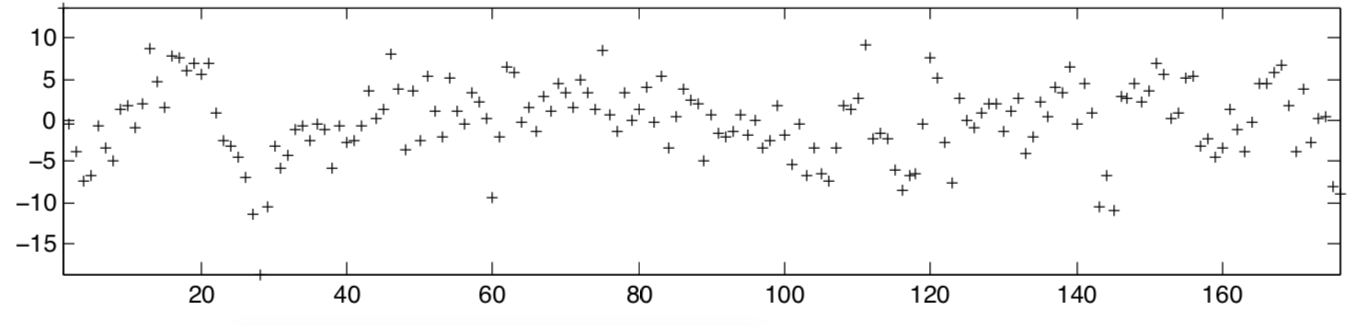
Simple random walk
\(Y_i\) i.i.d random variables \( \begin{cases} 1 & (\textrm{prob} \frac{1}{2}) \\ -1 & (\textrm{prob} \frac{1}{2}) \end{cases} \)
\(X_0, X_1, X_2, ...\) is called simple random walk.

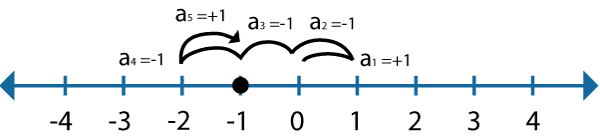
hard to visualize the time component
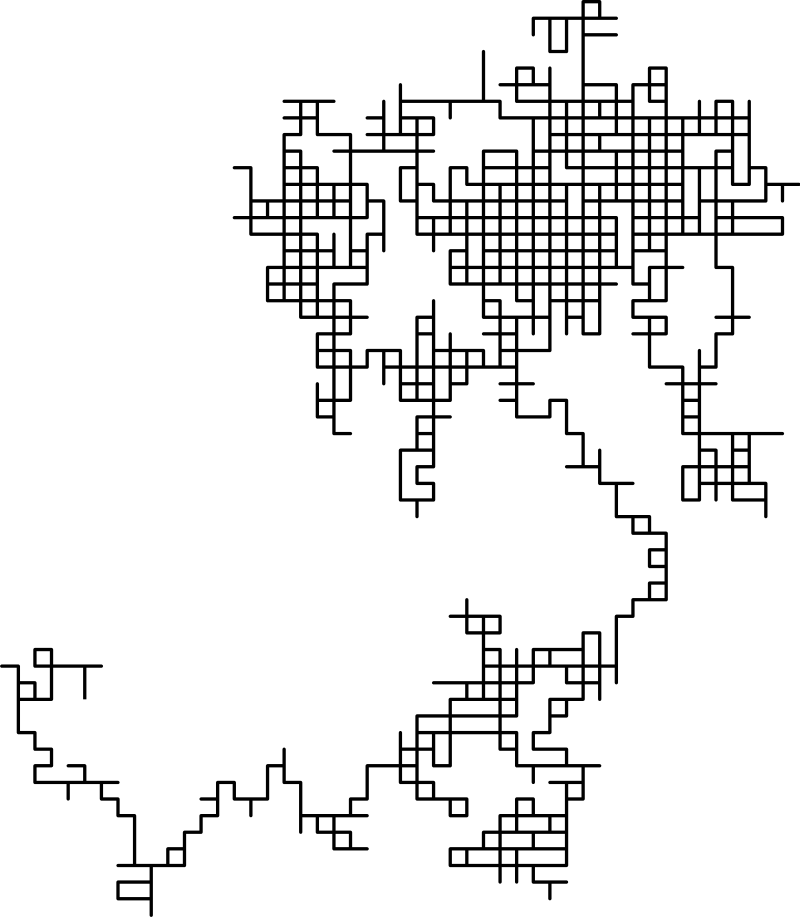
2-D simple random walk

Long term behavior?
Some properties
If \(0 = t_0\leq t_1 \leq \cdots \leq t_k\)
then \(X_{t_{i+1}}- X_{t_i}\) are mutally independent.
- \(E(X_k) = 0\)
- Independent increment
- Stationary
For all \(h \geq 1, t \geq 0\), the distribution of \(X_{t+h} - X_t\) is the same as the distribution of \(X_h\).
Example. A coin toss game...
At each turn, my balance goes up by $1 or down by $1.
My balance = Simple random walk
If I play until I win $100 or lose $100,
what is the probability of me winning?
If I play until I win $100 or lose $50,
what is the probability of me winning?
Code...
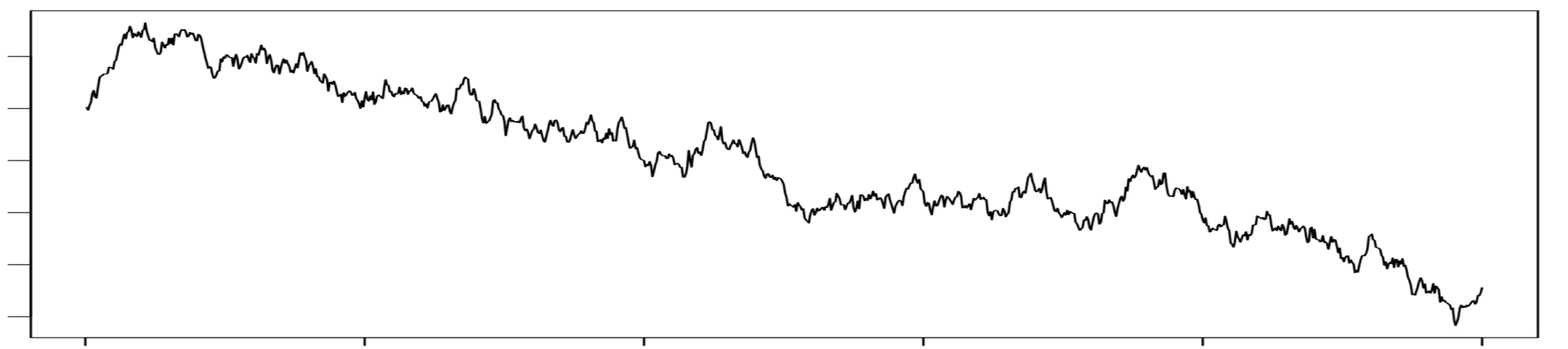
Brownian motion
is the "limit" of simple random walks.
Let \(Y_0, Y_1, ..., Y_n\) be a simple random walk.
\[Z\left(\frac{t}{n}\right) = Y_t\]
Interpolate linearly and take \(n \to \infty\).
Then, the resulting distribution is the Brownian motion.
A Markov chain
is a stochastic process where effect of the past on the future is summarized only by the current state.
Formally, ...
A discrete-time stochastic process \(X_0, X_1, X_2, ...\) with state space \(S\) has Markov property if
If the state space \(S\) (\(X_t \in S\)) is finite,
all the elements of a Markov chain model
can be encoded in a transition probability matrix.
Why?
transition probability
(jumping from state i to state j)
Is simple random walk a Markov chain?
Does simple random walk have a transition probability matrix?
This matrix contains all the information about the stochastic process.
Why?
What is the probability of going from state 7 to state 9 in one steps?
What is the probability of going from state 7 to state 9 in two steps?
\[P_{79}\]
\[P^2_{79}\]
What is the probability of going from state 7 to state 9 in \(n\) steps?
An unrealistic example...

What is our transition probability matrix?
state
state
Stationary distribution
Hidden Markov Model (HMM)
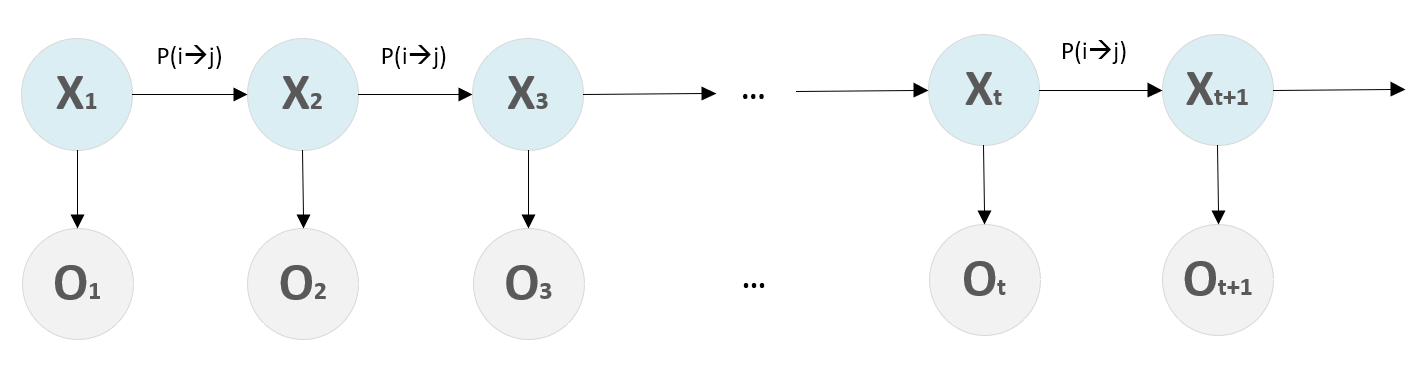
Hidden Markov Model (HMM)
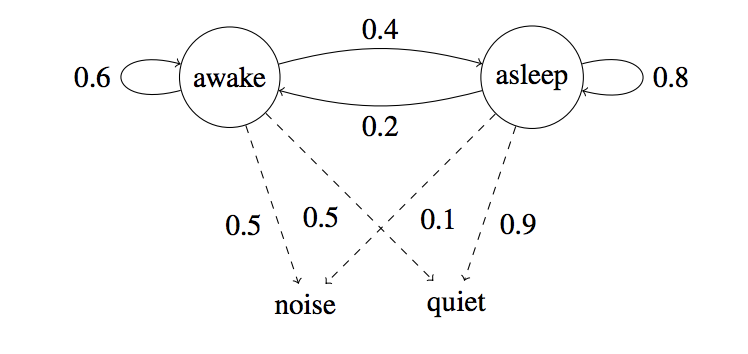
Hidden Markov Model (HMM)
Speech recognition
- Observation: sounds
- hidden states: words
Face detection
- Observation: overlapping rectangles of pixel intensities
- hidden states: facial features
DNA sequence region classification
- Observation: nucleotides
- Hidden states: introns, exons
A few words on
Markov Chain Monte Carlo method (MCMC)
A martingale
is a stochastic process which is "fair game".
Formally, ...
A discrete-time stochastic process \(X_0, X_1, X_2, ...\) is a martingale if
i.e., expected gain in the process is zero at all times.
Is a random walk a martingale?
A random variable \(X\) is distributed according to either \(f\) or \(g\). Consider a random sample \(X_1, \cdots, X_n\). Let \(Y_n\) be the likelihood ratio
\[Y_n = \prod_{i = 1}^n \frac {g(X_i)}{f(X_i)}\]
If X is actually distributed according to the density \(f\) rather than according to \(g\), then \[\{Y_n: n = 1, 2, 3, \cdots\}\] is a martingale with respect to\(\{X_n: n = 1, 2, 3, \cdots\}\).
Likelihood-ratio testing
Review
- Random walk
- Stochastic processes
- Markov chain
- Hidden Markov model
- MCMC
- Martingale