模擬退火
模擬退火
模擬退火(simulated annealing)是一個meta heuristic元啟發式的演算法
模擬退火
模擬退火(simulated annealing)是一個meta heuristic元啟發式的演算法
meta代表它可以解決很多不同面向的問題
模擬退火
模擬退火(simulated annealing)是一個meta heuristic元啟發式的演算法
meta代表它可以解決很多不同面向的問題
heuristic的意思代表它可以有效率地找到一個足夠好的解
模擬退火
模擬退火(simulated annealing)是一個meta heuristic元啟發式的演算法
meta代表它可以解決很多不同面向的問題
heuristic的意思代表它可以有效率地找到一個足夠好的解
meta有輔助heuristic的意思可以想成


meta
heuristic
模擬退火
模擬退火(simulated annealing)的想法是:
模擬退火
模擬退火(simulated annealing)的想法是:



高溫
冷卻
不純的礦石
還算純的金屬
模擬退火
模擬退火(simulated annealing)的大概步驟是:
1. 設定初始解和溫度(高溫), 降溫率, 執行次數
模擬退火
模擬退火(simulated annealing)的大概步驟是:
1. 設定初始解和溫度(高溫), 降溫率, 執行次數
2.開始冷卻過程,過程中越來越greedy
模擬退火
模擬退火(simulated annealing)的大概步驟是:
1. 設定初始解和溫度(高溫), 降溫率, 執行次數
2.開始冷卻過程,過程中越來越greedy
3.最後找出可能最佳解
模擬退火
以traveling salesman problem(TSP)為例
一個商人要造訪很多城市
模擬退火
以traveling salesman problem(TSP)為例
一個商人要造訪很多城市
他只能去每個城市一次,而要找到走最短的總路徑,最後回到原本的城市
模擬退火
以traveling salesman problem(TSP)為例
一個商人要造訪很多城市
他只能去每個城市一次,而要找到走最短的總路徑,最後回到原本的城市
這個問題若採用枚舉是O(N!) 非常大
模擬退火
以traveling salesman problem(TSP)為例
一個商人要造訪很多城市
他只能去每個城市一次,而要找到走最短的總路徑,最後回到原本的城市
這個問題若採用枚舉是O(N!) 非常大
因此通常採取模擬退火來解決
| 城市距離 | A | B | C | D | E |
|---|---|---|---|---|---|
| A | 0 | 3 | 7 | 4 | 2 |
| B | 3 | 0 | 9 | 1 | 3 |
| C | 7 | 9 | 0 | 2 | 2 |
| D | 4 | 1 | 2 | 0 | 7 |
| E | 2 | 3 | 2 | 7 | 0 |
範例
| 城市距離 | A | B | C | D | E |
| A | 0 | 3 | 7 | 4 | 2 |
| B | 3 | 0 | 9 | 1 | 3 |
| C | 7 | 9 | 0 | 2 | 2 |
| D | 4 | 1 | 2 | 0 | 4 |
| E | 2 | 3 | 2 | 7 | 0 |
假設他選擇走
A
| 城市距離 | A | B | C | D | E |
| A | 0 | 3 | 7 | 4 | 2 |
| B | 3 | 0 | 9 | 1 | 3 |
| C | 7 | 9 | 0 | 2 | 2 |
| D | 4 | 1 | 2 | 0 | 4 |
| E | 2 | 3 | 2 | 7 | 0 |
假設他選擇走
A
B
| 城市距離 | A | B | C | D | E |
| A | 0 | 3 | 7 | 4 | 2 |
| B | 3 | 0 | 9 | 1 | 3 |
| C | 7 | 9 | 0 | 2 | 2 |
| D | 4 | 1 | 2 | 0 | 4 |
| E | 2 | 3 | 2 | 7 | 0 |
假設他選擇走
A
B
C
| 城市距離 | A | B | C | D | E |
| A | 0 | 3 | 7 | 4 | 2 |
| B | 3 | 0 | 9 | 1 | 3 |
| C | 7 | 9 | 0 | 2 | 2 |
| D | 4 | 1 | 2 | 0 | 4 |
| E | 2 | 3 | 2 | 7 | 0 |
假設他選擇走
A
B
C
D
| 城市距離 | A | B | C | D | E |
| A | 0 | 3 | 7 | 4 | 2 |
| B | 3 | 0 | 9 | 1 | 3 |
| C | 7 | 9 | 0 | 2 | 2 |
| D | 4 | 1 | 2 | 0 | 4 |
| E | 2 | 3 | 2 | 7 | 0 |
假設他選擇走
A
B
C
D
E
| 城市距離 | A | B | C | D | E |
| A | 0 | 3 | 7 | 4 | 2 |
| B | 3 | 0 | 9 | 1 | 3 |
| C | 7 | 9 | 0 | 2 | 2 |
| D | 4 | 1 | 2 | 0 | 4 |
| E | 2 | 3 | 2 | 7 | 0 |
假設他選擇走
A
B
C
D
E
| 城市距離 | A | B | C | D | E |
| A | 0 | 3 | 7 | 4 | 2 |
| B | 3 | 0 | 9 | 1 | 3 |
| C | 7 | 9 | 0 | 2 | 2 |
| D | 4 | 1 | 2 | 0 | 7 |
| E | 2 | 3 | 2 | 7 | 0 |
這樣的路徑是 3+9+2+7+2 = 23
| 城市距離 | A | B | C | D | E |
| A | 0 | 3 | 7 | 4 | 2 |
| B | 3 | 0 | 9 | 1 | 3 |
| C | 7 | 9 | 0 | 2 | 2 |
| D | 4 | 1 | 2 | 0 | 7 |
| E | 2 | 3 | 2 | 7 | 0 |
但在這個的圖有120種走法哪一個才是最佳路徑呢?
| 城市距離 | A | B | C | D | E |
| A | 0 | 3 | 7 | 4 | 2 |
| B | 3 | 0 | 9 | 1 | 3 |
| C | 7 | 9 | 0 | 2 | 2 |
| D | 4 | 1 | 2 | 0 | 7 |
| E | 2 | 3 | 2 | 7 | 0 |
但在這個的圖有120種走法哪一個才是最佳路徑呢?
因此我們採取模擬退火求解
#include "bits/stdc++.h"
using namespace std;
int total_cost(vector <int>& tour, vector <vector <int>> &grid) {
int total = 0;
for (int i=0; i < tour.size()-1; i++) {
total += grid[tour[i]][tour[i+1]];
}
total += grid[tour[static_cast<int>(tour.size()-1)]][tour[0]];
return total;
}
vector <int> annealing(double temp, double cool_rate, int steps, vector <vector <int>>& grid) {
random_device rd;
mt19937 rng(rd());
uniform_int_distribution<int> newlocation (0, static_cast<int> (grid.size()) - 1);
vector <int> tour ((int)grid.size());
for (int i=0; i < grid.size(); i++) {
tour[i] = i;
}
shuffle(tour.begin(), tour.end(), rng);
int best_cost = total_cost(tour, grid);
vector <int> best_tour = tour;
int differ;
for (int step=0; step < steps; step++) {
int i = newlocation(rng), j = newlocation(rng);
if (i == j)
continue;
else
swap (tour[i], tour[j]);
int current_cost = total_cost(tour, grid);
differ = current_cost - best_cost;
if (differ < 0 || exp((static_cast <double>(-differ) / temp)) > static_cast <double>(rng()) / mt19937::max()){
if (differ < 0){
best_cost = current_cost;
best_tour = tour;
}
}
else
swap (tour[i], tour[j]);
temp *= cool_rate;
}
return best_tour;
}
int main() {
int n, m;
cin >> n >> m;
vector <vector <int>> grid (n, vector <int> (m));
for (int i=0; i < n; i++) {
for (int j=0; j < m; j++) {
cin >> grid[i][j];
}
}
double temp;
double cooling_rate;
int steps;
cin >> temp >> cooling_rate >> steps;
vector <int> tour;
tour = annealing(temp, cooling_rate, steps, grid);
int best = total_cost(tour, grid);
for (int v : tour) {
cout << v << " --> ";
}
cout << tour[0] << "\n";
cout << best;
}int main() {
int n, m;
cin >> n >> m;
vector <vector <int>> grid (n, vector <int> (m));
for (int i=0; i < n; i++) {
for (int j=0; j < m; j++) {
cin >> grid[i][j];
}
}
double temp;
double cooling_rate;
int steps;
cin >> temp >> cooling_rate >> steps;
vector <int> tour;
tour = annealing(temp, cooling_rate, steps, grid);
int best = total_cost(tour, grid);
for (int v : tour) {
cout << v << " --> ";
}
cout << tour[0] << "\n";
cout << best;
}n 為行, m 為列
輸入距離
初始溫度, 降溫速度, 執行次數
存取模擬退火的最佳路徑
輸出最後路徑 & 路徑長度
int total_cost(vector <int>& tour, vector <vector <int>> &grid) {
int total = 0;
for (int i=0; i < tour.size()-1; i++) {
total += grid[tour[i]][tour[i+1]];
}
total += grid[tour[static_cast<int>(tour.size()-1)]][tour[0]];
return total;
}total cost 算總路徑長
迴圈後再將最後的城市到初始城市的距離加回
vector <int> annealing(double temp, double cool_rate, int steps, vector <vector <int>>& grid) {
random_device rd;
mt19937 rng(rd());
uniform_int_distribution<int> newlocation (0, static_cast<int> (grid.size()) - 1);
vector <int> tour ((int)grid.size());
for (int i=0; i < grid.size(); i++) {
tour[i] = i;
}
shuffle(tour.begin(), tour.end(), rng);
int best_cost = total_cost(tour, grid);
vector <int> best_tour = tour;
int differ;函式回傳值是vector 因為最後回傳最佳路徑
random_device 取隨機種子碼
mt19937是 rng 它需要一個種子碼產生
uniform_int_distribution 產生 0 ~ (城市數-1) 的數字 (機率都一樣)
vector <int> annealing(double temp, double cool_rate, int steps, vector <vector <int>>& grid) {
random_device rd;
mt19937 rng(rd());
uniform_int_distribution<int> newlocation (0, static_cast<int> (grid.size()) - 1);
vector <int> tour ((int)grid.size());
for (int i=0; i < grid.size(); i++) {
tour[i] = i;
}
shuffle(tour.begin(), tour.end(), rng);
int best_cost = total_cost(tour, grid);
vector <int> best_tour = tour;
int differ;隨機產生初始路徑
預設最佳解為初始解
int differ;
for (int step=0; step < steps; step++) {
int i = newlocation(rng), j = newlocation(rng);
if (i == j)
continue;
else
swap (tour[i], tour[j]);
int current_cost = total_cost(tour, grid);
differ = current_cost - best_cost;
if (differ < 0 || exp((static_cast <double>(-differ) / temp)) > static_cast <double>(rng()) / mt19937::max()){
if (differ < 0){
best_cost = current_cost;
best_tour = tour;
}
}
else
swap (tour[i], tour[j]);
temp *= cool_rate;
}
return best_tour;differ - 現解與最佳解差異
挑選兩個點互換, 若點一樣則跳過
differ < 0 => 現解較佳
現解一定機率接受
降低接受機率 (降溫)
exp((static_cast <double>(-differ) / temp)) > static_cast <double>(rng()) / mt19937::max())程式核心
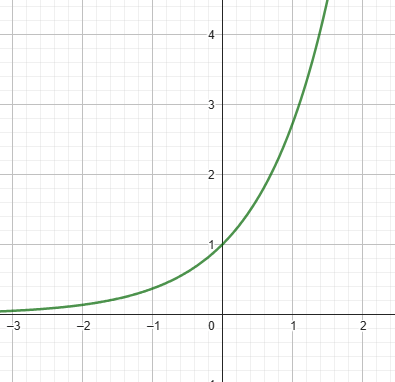
exp = e^x
e^x 取導數為 e^x
e 的變化率取決於當時的值
當differ大或temp小,e^x趨近於0
使用其與 rng / rng的max比