TLE[0]

講師自介

講師自介

  • 林禹喆
  • dc: Treeman
  • 資訊社教學
  • 因為想學演算法, 所以來當算法講師

Table

Bruteforce

State Space Tree

Pruning

Backtracking

Bitmask

Meet in the Middle

Divide and Conquer

Merge Sort

Binary Search

Sparse Table

Binary Lifting

Segment Tree

Bruteforce

Bruteforce?

Bruteforce?

  • 中文翻譯是暴力

  • 簡單來說就是窮舉答案然後選出最佳解

  • 因為複雜度很高, 所以通常在範圍小的題目使用

Bruteforce?

  • 中文翻譯是暴力

  • 簡單來說就是窮舉答案然後選出最佳解

  • 因為複雜度很高, 所以通常在範圍小的題目使用

  • 枚舉時, 要清楚該枚舉什麼

例題:

B - Count Subgrid

給你一個\:N\times N\:的矩陣\newline 第i行第j列為黑色\: \# \:或白色 \: . \newline 問有幾個相異的M\times M的矩陣
\bullet\:{1 \leq M \leq N \leq 10}\newline
\bullet\:{S_{i, j} \rightarrow \# \:or\: .}
N如果很小, 可以想想看枚舉解法\newline
N如果很小, 可以想想看枚舉解法\newline 該怎麼枚舉?\newline
考慮對於每一個M\times M矩陣\newline 擷取他的狀態然後丟進一個set裡面維持相異性

Code:

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int h, m;
    cin >> h >> m;
    
    vector<string> grid(h);
    for (int i=0; i < h; i++)
        cin >> grid[i];
    set<vector<string>> saves;
    for (int i=0; i <= (h-m); i++)
        for (int j=0; j <= (h-m); j++)
        {
            vector<string> g(m);
            for (int ti = 0; ti < m; ti++)
                for (int tj = 0; tj < m; tj++)
                    g[ti].push_back(grid[i+ti][j+tj]);
  
            saves.insert(g);
        }
    cout << saves.size();
}
# PRESENTING CODE

例題:

Chessboard and Queens

給你一個\:8\times 8\:的棋盤\newline 第i行第j列為已佔據\: * \:或空格 \: . \newline 問有幾個放入八個皇后的方式\newline 讓最後兩兩不互相攻擊
\bullet\:{S_{i, j} \rightarrow * \:or\: .}

想法:

對於每一行的每一列

放入一個當下情況允許的皇后

當第8行放完時就結束了

Code:

#include <bits/stdc++.h>
using namespace std;
 
vector<vector<char>> saves(8, vector <char> (8));
unordered_map<int, int> pieces;
int ans = 0;
 
bool check_valid(int y, int x) 
{
 
    if(saves[y][x] != '*') 
    {
 
        for (int i=0; i < y; i++) 
        {
            if (pieces[i] - x == i - y)
                return false;
 
            if (pieces[i] == x)
                return false;
            
            if (pieces[i] + i == x + y)
                return false;
 
        }
 
        return true;
    }
    else
        return false;
}
 
void solution(int row) 
{
 
    if (row == 8) 
    {
 
        ans++;
        return;
    }
    
    for (int i=0; i < 8; i++) 
    {
 
        if (!check_valid(row, i)) 
            continue;
            
        pieces[row] = i;
 
        solution(row + 1);
 
        pieces.erase(row);
    }
 
}
 
signed main() {
 
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    for (int i=0; i < 8; i++) 
        for (auto &x : saves[i])
            cin >> x;
 
    solution(0);
    
    cout << ans;
}
# PRESENTING CODE

例題:

Apple Division

給你N個蘋果\newline 第i個蘋果的重量是P_{i}\newline 問如何平分蘋果使兩堆的重量差最小
\bullet\:{1 \leq N \leq 20}\newline
\bullet\:1 \leq P_{i} \leq 10^9

想法:

枚舉0/1狀態

想法:

枚舉0/1狀態

0/1狀態為何

想法:

枚舉0/1狀態

0/1狀態為何

一個數字在二進制由許多0/1組成

想法:

枚舉0/1狀態

0/1狀態為何

一個數字在二進制由許多0/1組成

把1當作取, 0當作不取

想法:

枚舉0/1狀態

0/1狀態為何

一個數字在二進制由許多0/1組成

把1當作取, 0當作不取

如此即可以枚舉

mask = 0 \sim 2^n - 1

Code:

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
 
int main() 
{
    int n;
    cin >> n;
 
    vector<ll> saves(n);
    for (int i = 0; i < n; i++) 
        cin >> saves[i];
 
    ll total = accumulate(saves.begin(), saves.end(), 0LL);
    ll ans = LLONG_MAX;
 
    for (int mask = 0; mask < (1 << n); mask++) 
    {
        ll sum1 = 0;
        for (int i = 0; i < n; i++) 
            if (mask & (1 << i)) 
                sum1 += saves[i];    
        
        ll sum2 = total - sum1;
        ans = min(ans, abs(sum1 - sum2));
    }
 
    cout << ans << '\n';
}
# PRESENTING CODE

例題:

Grid Path Description

給你一個\:7\times 7的矩陣和一個字串\newline 字串由U,D,L,R,?\:組成,?代表當下如何移動未知\newline 問有幾個走法能從(0,0)走到(0,6)
S = 48

想法:

想法:

對於現在走到的每一步,

 

想法:

對於現在走到的每一步,

如果下一步未知,

上下左右都試走一遍

可是這樣複雜度會變成\mathcal{O}(4^{n^2})
可是這樣複雜度會變成\mathcal{O}(4^{n^2})\newline 所以我們必須優化現在的想法

Pruning - 剪枝

Pruning - 剪枝

如果發現對於現在的狀況繼續走不會帶來解

Pruning - 剪枝

如果發現對於現在的狀況繼續走不會帶來解

砍掉這一個枝點

Pruning - 剪枝

如果發現對於現在的狀況繼續走不會帶來解

砍掉這一個枝點

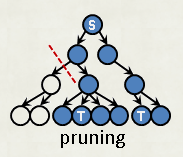
Pruning - 剪枝

注意到當:

  • 到達(0, 6)卻還沒走到48步時
  • 上下堵住,左右卻還沒走過時
  • 左右堵住,上下卻還沒走過時

Pruning - 剪枝

注意到當:

  • 到達(0, 6)卻還沒走到48步時
  • 上下堵住,左右卻還沒走過時
  • 左右堵住,上下卻還沒走過時

我們不會有解, 因此可以砍掉這整個分支

Code:

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
 
string s;
bool visited[7][7];
int ans = 0;
 
void dfs(int i, int j, int steps = 0) 
{
 
    if (i == 6 && j == 0) 
    {
        if (steps != 48)
            return;
        ++ans;
    }
 
    if ((i == 0 || visited[i - 1][j]) && (i == 6 || visited[i + 1][j]) && j > 0 && j < 6 && !visited[i][j - 1] && !visited[i][j + 1]) 
    {
        visited[i][j] = false;
        return;
    }
 
    if ((j == 0 || visited[i][j - 1]) && (j == 6 || visited[i][j + 1]) && i > 0 && i < 6 && !visited[i - 1][j] && !visited[i + 1][j]) 
    {
 
        visited[i][j] = false;
        return;
    }
 
    visited[i][j] = true;
    if (s[steps] == '?' || s[steps]  == 'U') 
        if ( i && !visited[i-1][j]) 
            dfs(i-1, j, steps + 1);

    if (s[steps] == '?' || s[steps]  == 'D') 
        if ( i < 6 && !visited[i+1][j]) 
            dfs(i+1, j, steps + 1);
        
    
    if (s[steps] == '?' || s[steps]  == 'L') 
        if ( j && !visited[i][j-1]) 
            dfs(i, j-1, steps + 1);
    
    if (s[steps] == '?' || s[steps]  == 'R') 
        if ( j < 6 && !visited[i][j+1]) 
            dfs(i, j+1, steps + 1);
        
    visited[i][j] = false;
}
 
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
 
    cin >> s;
    dfs(0, 0);
 
    cout << ans;
}
# PRESENTING CODE

練習題:

Divide and Conquer

Divide and Conquer?

  • 中文翻譯是分而治之

  • 如果現在的問題不好解決就把問題拆成小問題然後一直重複直到小問題可以直接求解,最後合併回答大問題

Divide and Conquer?

  • 中文翻譯是分而治之

  • 如果現在的問題不好解決就把問題拆成小問題然後一直重複直到小問題可以直接求解,最後合併回答大問題

  • 很多題目都有分治解, 但分治不一定是唯一解而且分治不好想,所以用分治前要想清楚

例題:

Sort List

給你一個linked list的頭

回傳排序完成後, linked list的頭

\bullet \:n \leq 5\times 10^4\newline \bullet \:-10^5 \leq x_{i} \leq 10^5
為了維持\mathcal{O}(1)\: space\:和\: \mathcal{O}(n \log{n})\: time \newline 另外開一個陣列存或\newline 用跳來跳去的排序演算法也不行了\newline (比如:heap \: sort,\: quick \: sort....)\newline 因此我們採取merge \: sort求解

想法

Code:

#include <bits/stdc++.h>
using namespace std;

// struct ListNode 
// {
//     int val;
//     ListNode *next;
//     ListNode() : val(0), next(nullptr) {}
//     ListNode(int x) : val(x), next(nullptr) {}
//     ListNode(int x, ListNode *next) : val(x), next(next) {}
// };

class Solution {
public:
    ListNode* sortList(ListNode* head) 
    {
        if (!head || !head->next) return head;
        auto slow = head, fast = head->next;

        while (fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
        }
        auto mid = slow->next;
        slow->next = nullptr;

        return merge(sortList(head), sortList(mid));
    }
private:
    ListNode* merge(ListNode* l, ListNode* r)
    {
        ListNode dummy;
        ListNode* tail = &dummy;
        
        while (l && r)
        {
            if (l->val > r->val) swap(l, r);
            tail->next = l;
            l = l->next;
            tail = tail->next;

        }
        if (l) tail->next = l;
        if (r) tail->next = r;
        return dummy.next;
    }
};
# PRESENTING CODE

例題:

Count of Range Sum

給你一個陣列\: nums \:和lower, upper兩整數\newline 回傳有幾個區間和介於\:[lower, upper]\: 之間 \newline 即 \: lower \leq \sum_{i\: = \: l}^{r}{x_{i}} \leq upper
\bullet 1 \leq nums.size \leq 10^5
\bullet -2^{31} \leq nums[i]\leq 2^{31} - 1
\bullet -10^5 \leq l, r\leq 10^5
枚舉並排序所有區間和\newline n + (n-1) + (n-2)... \longrightarrow \mathcal{O}(n^2\log{n^2}) \newline

想法

枚舉並排序所有區間和\newline n + (n-1) + (n-2)... \longrightarrow \mathcal{O}(n^2\log{n^2}) \newline n = 1000, AC \newline n = 1e5, TLE 😡

想法

首先注意到當有兩前綴和\newline prefix[i], prefix[j] 且 i < j\newline 則prefix[j] - prefix[i] \newline 構成一個區間和

想法

考慮使用類似merge \: sort的概念求解 \newline 注意到當左右兩邊前綴和有排序過\newline 則對於每一個左界l\newline 都有prefix[k] - prefix[l] < lower \newline prefix[j] - prefix[l] <= upper \newline 因此\: j - k \: 就是對於這個左界和這個範圍\newline 所有的符合條件的subarray \: sum

想法

Code:

using ll = long long;

class Solution 
{
public:
    int countRangeSum(vector<int>& nums, int lower, int upper)
    {
        int n = nums.size();
        vector<ll> prefix(n+1);
        for (int i=0; i < n; i++) prefix[i+1] = prefix[i] + nums[i];
        
        return sort(prefix, 0, n+1, lower, upper);
    }

    int sort(vector<ll> &prefix, int l, int r, int &lower, int &upper)
    {
        if (r - l <= 1) return 0;

        int mid = (l + r) >> 1;
        int count = sort(prefix, l, mid, lower, upper) + sort(prefix, mid, r, lower, upper);

        int j = mid, k = mid;
        for (int i=l; i < mid; i++)
        {
            while (k < r && prefix[k] - prefix[i] < lower) k++;
            while (j < r && prefix[j] - prefix[i] <= upper) j++;
            count += j-k;
        }
        
        inplace_merge(prefix.begin()+l, prefix.begin()+mid, prefix.begin()+r);

        return count;
    }
};

# PRESENTING CODE

例題:

Static Range Minimum Queries​

給你一個大小為n的陣列和q筆詢問\newline 對於每一個詢問\:q\:, 求[a, b]範圍的最小值
\bullet 1 \leq n, q \leq 2 \times 10^5
\bullet 1 \leq a \leq b \leq n
\bullet 1 \leq x_{i} \leq 10^9
對於每筆詢問\newline 直接枚舉找所有介於[a, b]之值\newline

想法

對於每筆詢問\newline 直接枚舉找所有介於[a, b]之值\newline time \: complexity: \mathcal{O}(q\times n) \newline TLE😇😇😇

想法

有沒有更好的詢問複雜度? \newline 例如 \mathcal{O}(\sqrt{n}), \mathcal{O}(\log{n})甚至是\mathcal{O}(1)

想法

其實都有
把陣列切成\sqrt{n}\:個大小為\sqrt{n}\:的方塊\newline 對於每一個\sqrt{n}\:大小的區間, 求出其最小值\newline 如此每一筆查詢就可以在3個\sqrt{n}\:時間內完成

想法

具體想法如下\newline
如果[a, b]之間有k個大小為\sqrt{n}\:的格子 \newline 可以在\mathcal{O}(k)時間內完成查詢最小值\newline 對於沒有落在所選取格子內的數字\newline 直接暴搜, 可以在2個\sqrt{n}\:時間內解決
複雜度per\: query \newline \mathcal{\Theta}(k + 2 \times \sqrt{n})
計算一下: \newline 2 \times 10^5 \times 3 \times \sqrt{2 \times 10^5} > 10^8 \newline TLE ?😨 \newline
計算一下: \newline 2 \times 10^5 \times 3 \times \sqrt{2 \times 10^5} > 10^8 \newline TLE ?😨 \newline 看你有沒有優化

Code:

#include <bits/stdc++.h>
#pragma GCC optimize("Ofast,unroll-loops")
using namespace std;

int main()
{
    cin.tie(nullptr)->sync_with_stdio(false);

    int n, q;
    cin >> n >> q;

    int b = sqrt(n) + 1;
    int saves[n], blocks[b];
    memset(blocks, 0x3f, sizeof(blocks));

    for (int i=0; i < n; i++)
        cin >> saves[i], blocks[i/b] = min(blocks[i/b], saves[i]);
    
    while (q--)
    {
        int l, r;
        cin >> l >> r;
        --l, --r;

        int ans = INT_MAX;
        for (int i=l; i <= r;)
            if (i % b == 0 && i + b - 1 <= r)
                ans = min(ans, blocks[i/b]), i += b;
            else
                ans = min(ans, saves[i]), ++i;

        cout << ans << '\n';
    }
}
# PRESENTING CODE
考慮類似merge\:sort的概念 \newline 存取每一個切半的區間的最小值 \newline 如此從根節點往下走\newline 取包含[a, b]區間的節點\newline 最多會造訪4\times \log{n}個子節點

想法

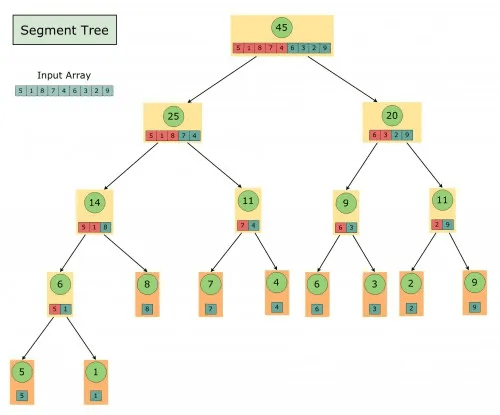
概念大概如下:

計算一下: \newline 2 \times 10^5 \times 4 \times \log_{2}({2 \times 10 ^ 5)} < 2 \times 10^7 \newline 耶 😎😎😎

Code:

#include <bits/stdc++.h>
using namespace std;
 
int n, q;
const int MAXN = 2e5 * 4 + 10;
static int saves[MAXN];
static int st[MAXN];

void build(int v, int tl, int tr)
{
    if (tl == tr)
        st[v] = saves[tl];
    else
    {
        int m = (tl + tr) >> 1;
        build(v*2, tl, m), build(v*2 + 1, m+1, tr);
        st[v] = min(st[v*2], st[v*2 + 1]);
    }
}
int getmin(int v, int l, int r, int tl = 1, int tr = n)
{
    if (tl > r || tr < l)
        return INT_MAX;
    if (l <= tl && tr <= r)
        return st[v];
    int m = (tl + tr) >> 1;
    return min(getmin(v*2, l, r, tl, m), getmin(v*2 + 1, l, r, m+1, tr));
}
int main()
{
    cin.tie(nullptr)->sync_with_stdio(false);
    cin >> n >> q;
    for (int i=1; i <= n; i++)
        cin >> saves[i];
    build(1, 1, n);
 
    while (q--)
    {
        int b, c;
        cin >> b >> c;
        
        cout << getmin(1, b, c) << '\n';
    }
}
# PRESENTING CODE
考慮對於每一個2的冪次方區間\newline 存取其最小值\newline 當要詢問時\newline 假設\:k=\log_{2}(b - a)捨去小數後的區間 \newline 則答案顯而易見在 \newline a \sim a + k, b-k \sim b 之間 \newline 直接從我們建的表裡面取答案

想法

Code:

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 114514;
 
static int st[22][MAXN+5];
int main()
{
    int n, q; 
    cin >> n >> q;
    
    for (int i=0; i < n; i++) 
    	cin >> st[0][i];
 
    for (int i=1; (1 << i) <= n; i++)
        for (int j=0; j + (1 << i) - 1 <= n; j++)
            st[i][j] = min(st[i-1][j], st[i-1][j + (1 << (i-1))]);
           
    while (q--)
    {
        int l, r; 
        cin >> l >> r;
        l--, r--;
        
        int k = __lg(r-l + 1);
        cout << min(st[k][l], st[k][r-(1 << k) + 1]) << '\n';
    }
    
}
# PRESENTING CODE

例題:

Increasing Array Queries

給你一個大小為n的陣列和q筆詢問 \newline 對於每一筆詢問q_{i} 給定[a,b] \newline 計算如果[a, b]區間為非嚴格遞增\newline 與原本的區間和差多少
\bullet 1 \leq n, q \leq 2 \times 10^5
\bullet 1 \leq x_{i} \leq 10^9
\bullet 1 \leq a \leq b \leq n
直接枚舉\newline 每一筆詢問為\mathcal{O}(n) \newline TLE 😡😡😡😡😡😡

想法

考慮對於每一個數字(假設在index \: i)\newline 存取第一個大於自己的數字(假設在index \: j)\newline 為了保持非嚴格遞減這段的修改大小為\newline x_{i} * (j - i - 1) - (prefix[j] - prefix[i]) \newline 對於每一個2的冪次方區間\newline 存取這一格往後跳\: 2^k \:格的修改大小\newline 如此一來就可以在每筆詢問\mathcal{O}(\log n)回答\newline

想法

假如在[a, b]\newline 已經沒有比現在數字大的數字\newline h_{a}\times (b-a) - (prefix[b] - prefix[a])\newline

想法

Code:

#include <bits/stdc++.h>
#pragma GCC optimize("Ofast")
using namespace std;
#define int long long
using ll = long long;
 
const int MAXN = 2e5 + 67;
int n, q;
struct seg
{
    int r;
 
    ll c;
} jp[21][MAXN];
 
ll pref[MAXN], npref[MAXN];
int saves[MAXN];
 
signed main()
{
    cin.tie(nullptr)->sync_with_stdio(false);
    cin >> n >> q;
 
    for (int i=1; i <= n; i++)
        cin >> saves[i], pref[i] = pref[i-1] + saves[i];
    
    stack<int> st;
    for (int i=1; i <= n; st.push(i), i++)
        while (!st.empty() && saves[i] > saves[st.top()])
            jp[0][st.top()] = {i, saves[st.top()] * (i - st.top() - 1) - (pref[i-1] - pref[st.top()])}, st.pop();
 
 
    for (int i=1; i <= 20; ++i)
        for (int j=1; j <= n; j++)
            jp[i][j] = {jp[i-1][jp[i-1][j].r].r, jp[i-1][j].c + jp[i-1][jp[i-1][j].r].c};
 
    while (q--)
    {
        int a, b;
        cin >> a >> b; 
 
        ll ans = 0;
        if (a == b) { cout << ans << '\n'; continue;}
 
        int h = saves[a];
        for (int i = __lg(b-a); i >= 0; --i)
            if (jp[i][a].r != 0 && jp[i][a].r <= b)
                ans += jp[i][a].c, a = jp[i][a].r, h = saves[a];
        
        cout << ans + 1LL * h * (b-a) - (pref[b] - pref[a]) << '\n';
    }
}
# PRESENTING CODE

練習題:

PadOrU PaDoRu

Made with Slides.com