基礎圖論
Basic Graph Theorem by PolarisChiba
講師介紹
-
姓名:李昕威
-
PolarisChiba
-
清大準大一生
講台上這個人
名詞介紹
你要怎麼你和你隔壁的人的不同
答案的關鍵就在名字......
無向圖
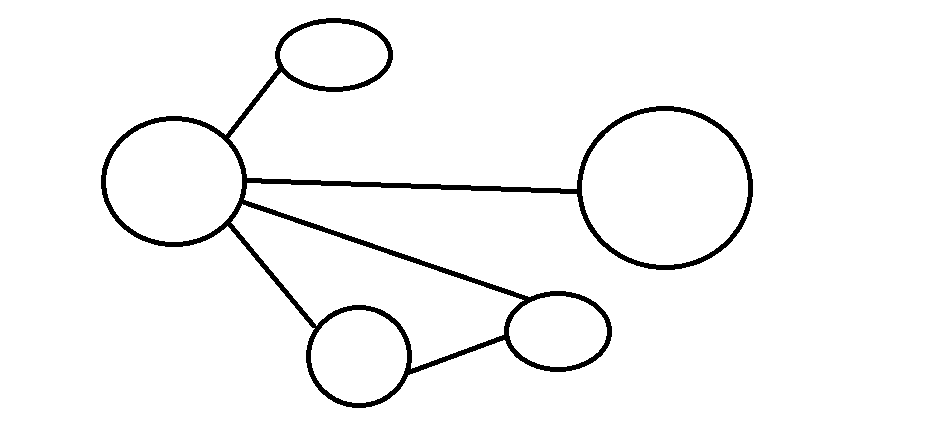
邊沒有方向
有向圖
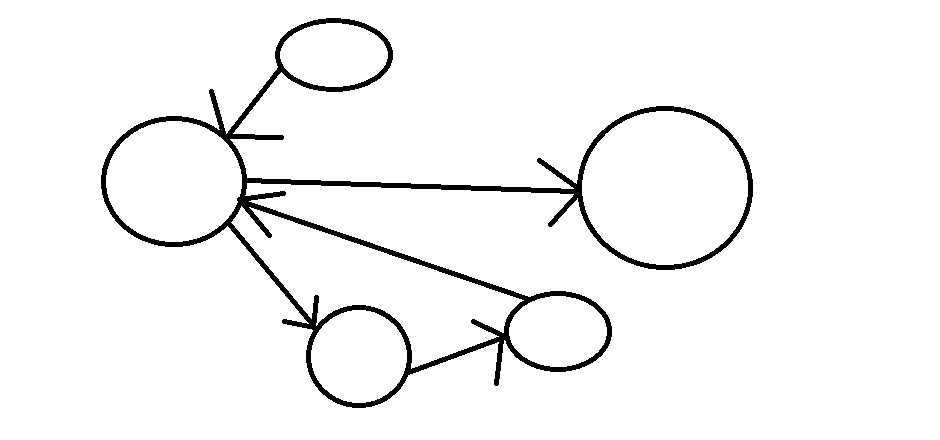
邊有方向
相鄰
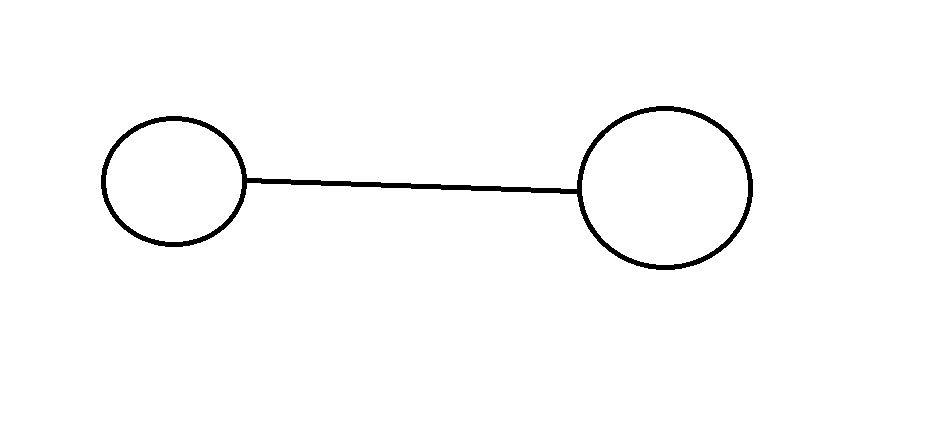
兩點用一條邊連接
度數
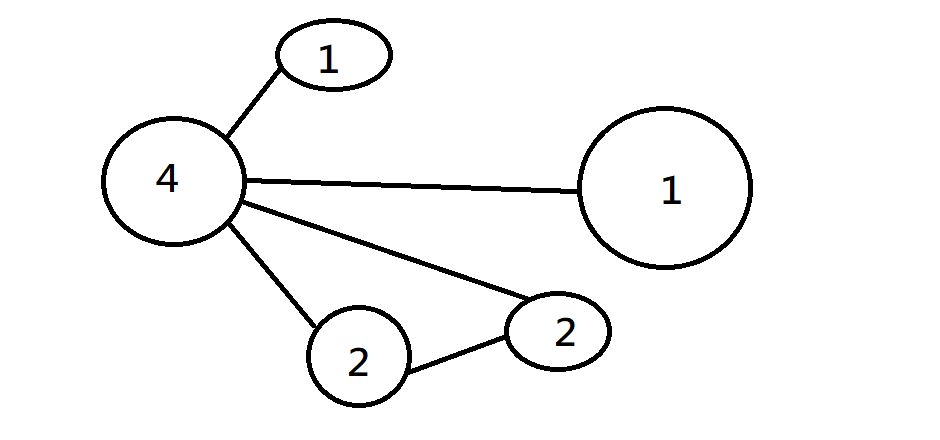
與一個點相鄰的邊數
度數(有向圖)
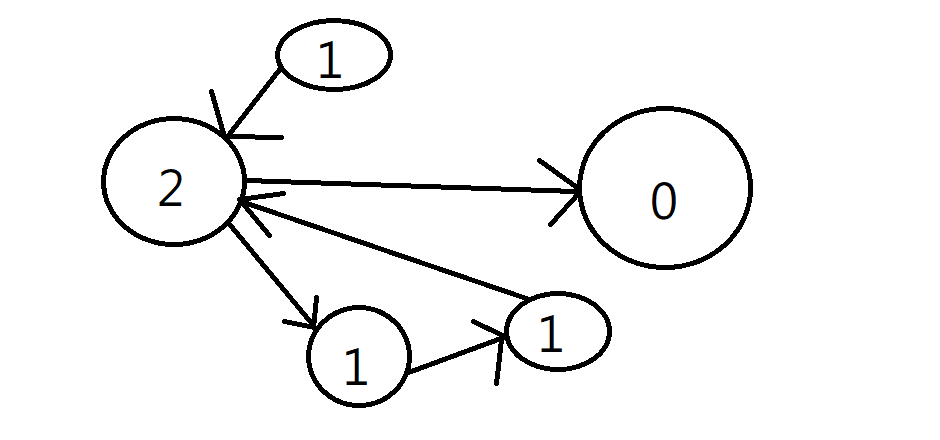
出度
度數(有向圖)
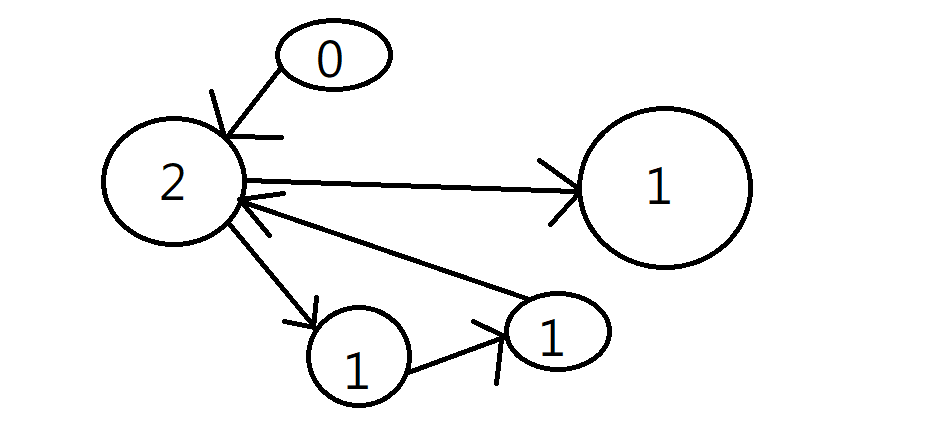
入度
點權

點上的數值
邊權
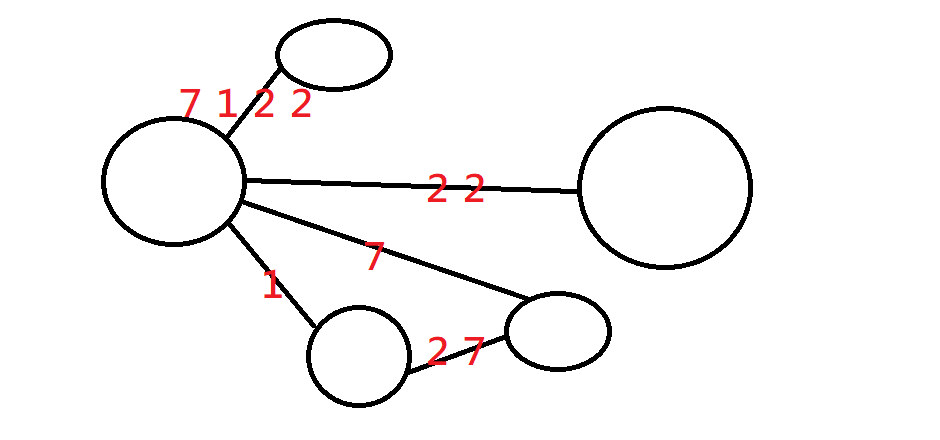
邊上的數值
路徑
連續的邊的序列
環
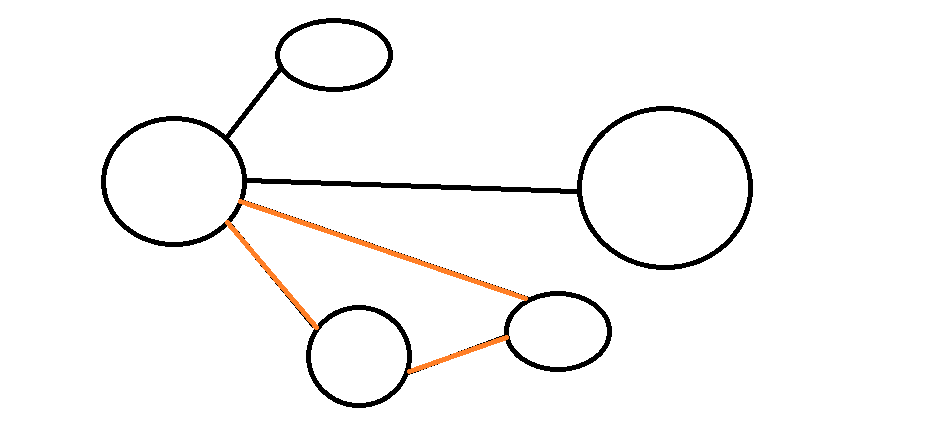
起點與終點相同的路徑
自環
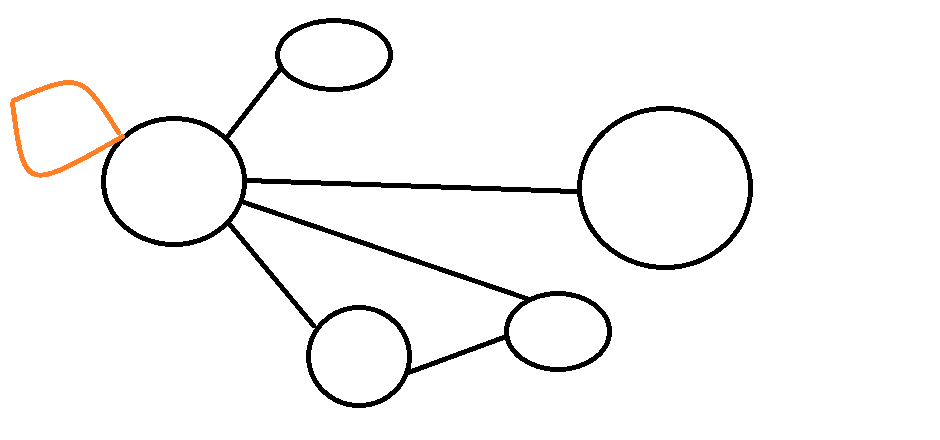
一條自己連到自己的邊
子圖
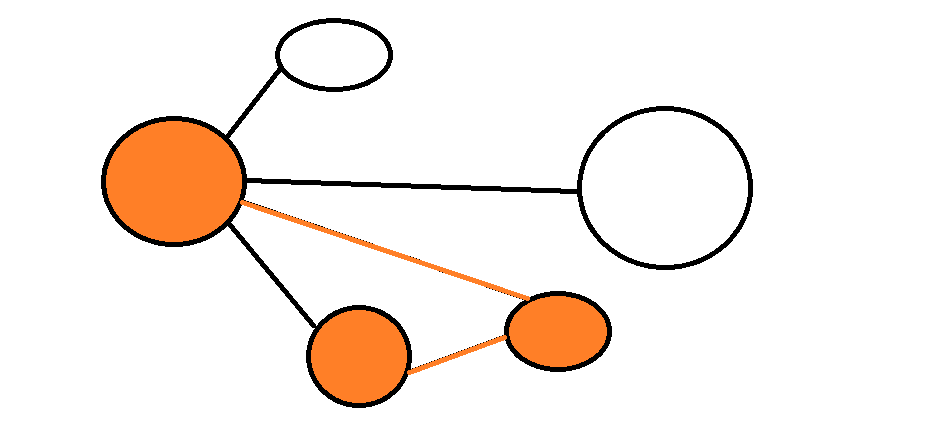
由原圖中的一些點和邊所組成的圖
反正一次講這麼多也記不住吧
圖的表示法
你要怎麼分辨你左邊和右邊的人的不同?
答案的關鍵或許就在長相......
圖的表示法
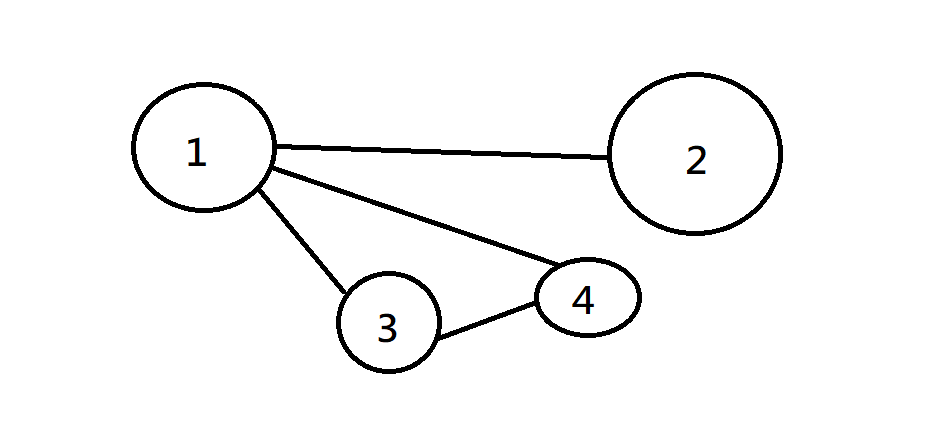
要如何表達邊與點的關係呢?
鄰接矩陣

直接看兩個點是否相鄰
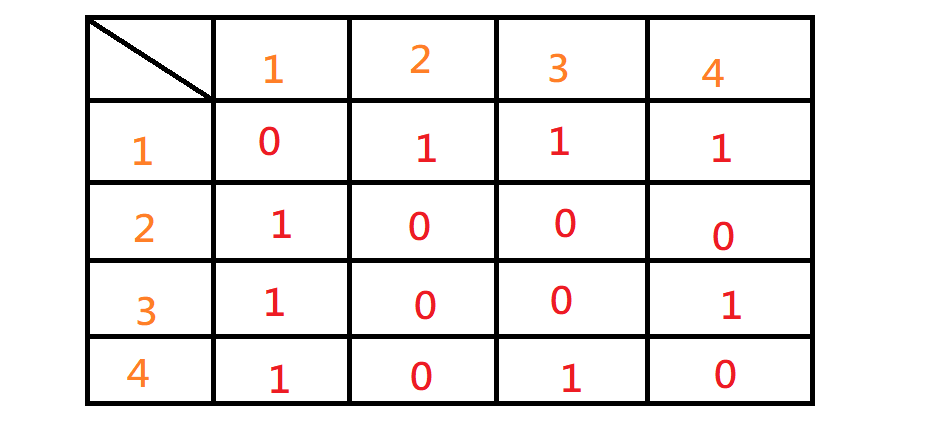
鄰接矩陣
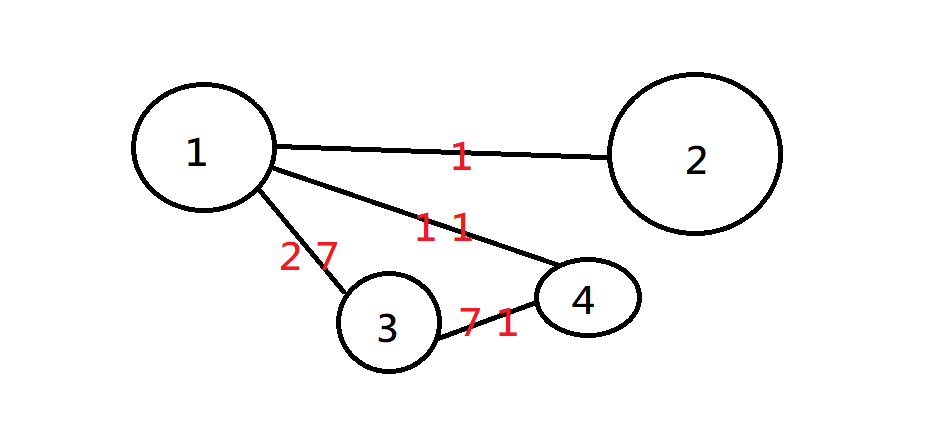
兩個點之間的邊權
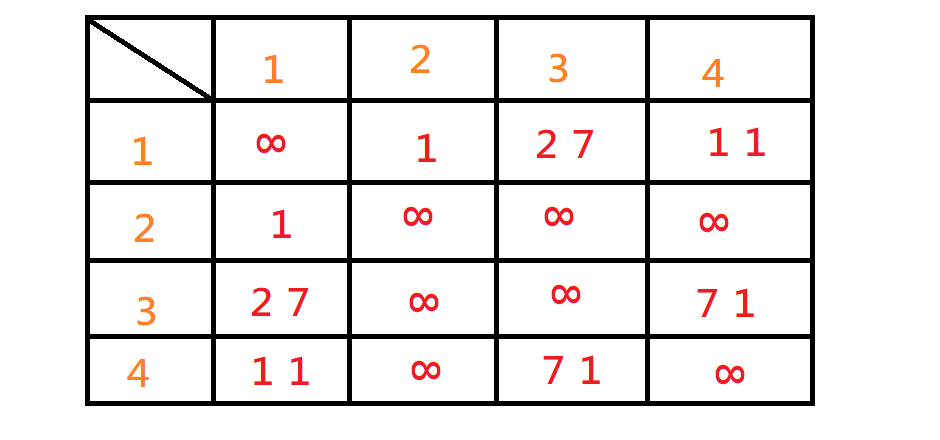
鄰接矩陣
兩個點之間的邊權
int G[N][N];
for (int i = 1; i <= m; ++i) {
int a, b;
cin >> a >> b;
G[a][b] = 1;
// G[b][a] = 1;
}
for (int i = 1; i <= m; ++i) {
int a, b, w;
cin >> a >> b >> w;
G[a][b] = w;
// G[b][a] = w;
}空間複雜度太高了ORZ
鄰接串列

看一個點和哪些點相鄰
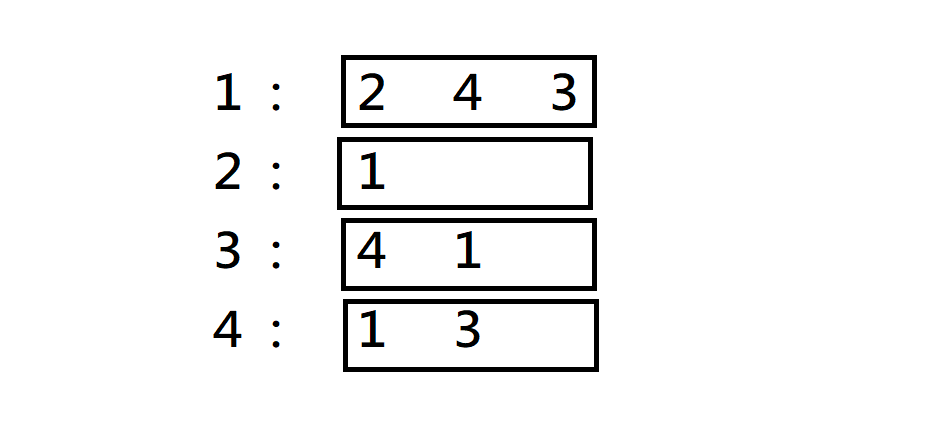
鄰接串列

看一個點和哪些點相鄰
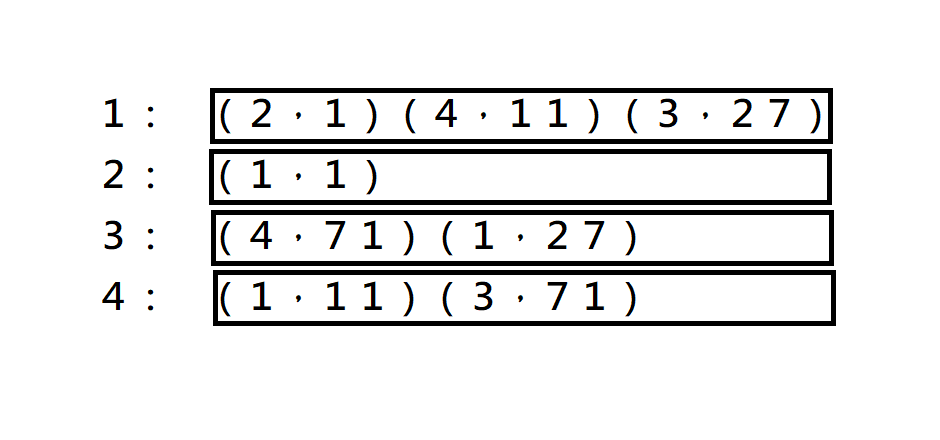
鄰接串列
vector<int> v[N];
for (int i = 0; i < m; ++i) {
int a, b;
cin >> a >> b;
v[a].push_back(b);
}
vector<pair<int,int>> v[N];
for (int i = 0; i < m; ++i) {
int a, b, w;
cin >> a >> b >> w;
v[a].push_back(make_pair(b, w));
v[b].push_back(make_pair(a, w));
}圖的遍歷
你是如何從清大校門口走到這裡的?
如果沒有地圖、沒有網路的話,你恐怕必須學會這一招
圖的遍歷
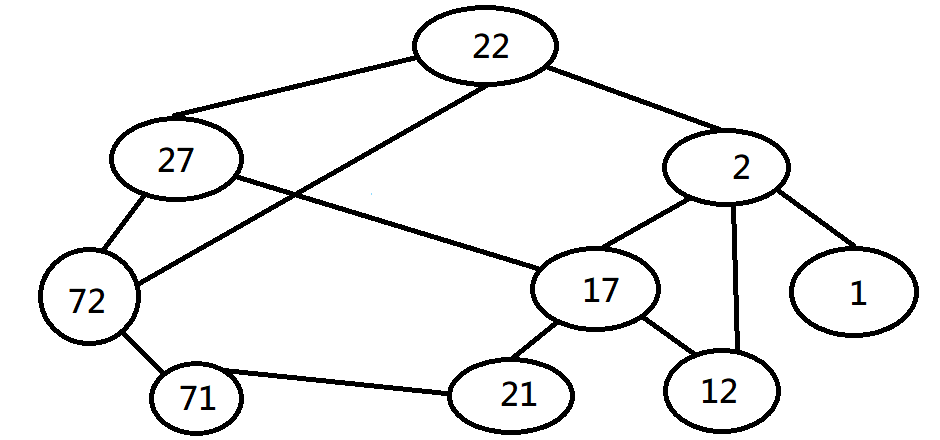
有甚麼方法可以在O(V)的時間內走過整張圖呢?
深度優先探訪 DFS
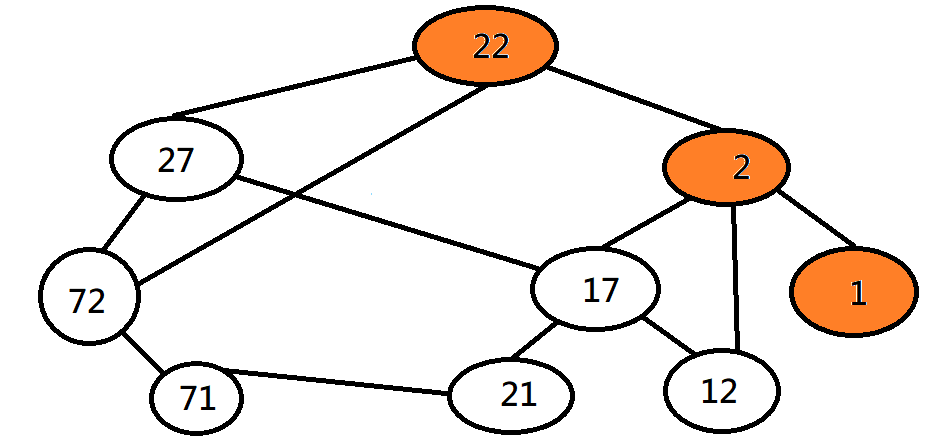
總之就先一直走,走到底
深度優先探訪 DFS
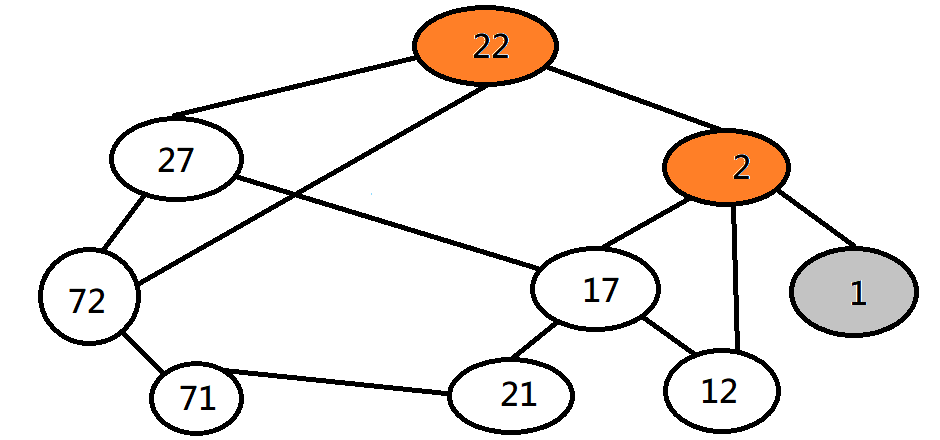
不能走的時候退回來,並標示走過了
深度優先探訪 DFS
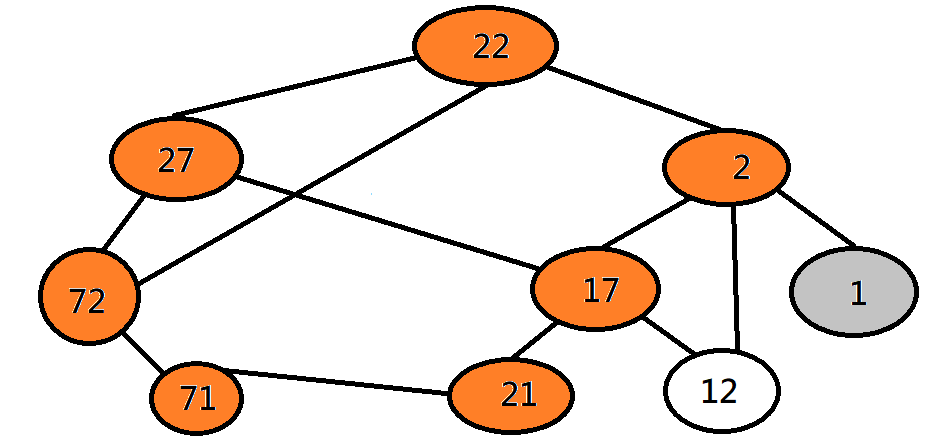
繼續從其他能走的點走下去
深度優先探訪 DFS
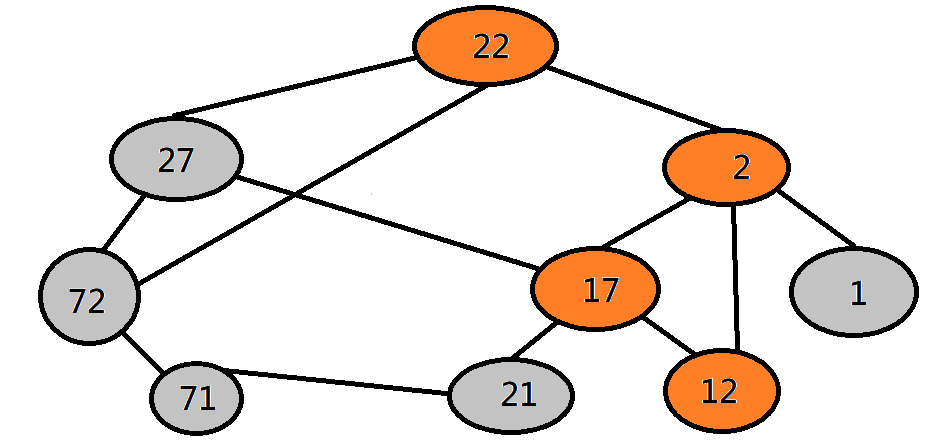
退回來、走下去
深度優先探訪 DFS
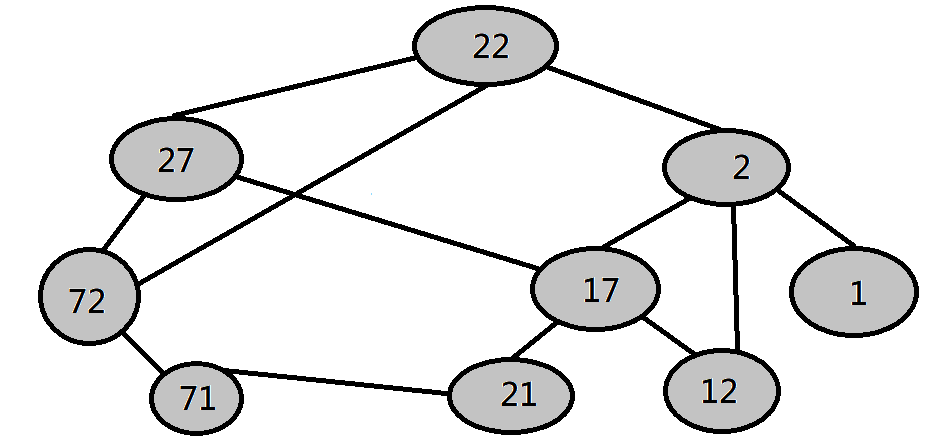
退回原點,完成
深度優先探訪 DFS
bool visited[N];
vector<int> v[N];
void dfs(int x) {
visited[x] = 1;
for (auto i : v[x]) if (!visited[i]) {
// do something
dfs(i);
}
}例題演練
佔邊砍樹
佔邊砍樹
相鄰兩點至少要有一點被佔領
佔邊砍樹
bool visited[N];
int color[N];
vector<int> v[N];
void dfs(int x, int color) {
vistited[x] = 1;
col[x] = color;
bool ok = 1;
for (auto i:v[x]) {
if (!visited[i]) dfs(i, 1 - color);
}
}
//最後統計color為1 與為 0各有多少
//比較多的就是答案寬度優先探訪 BFS
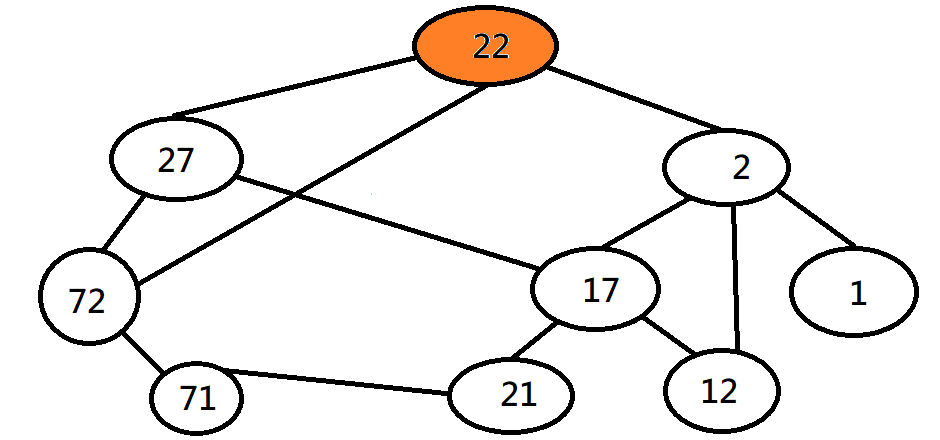
一層一層搜尋下去
寬度優先探訪 BFS
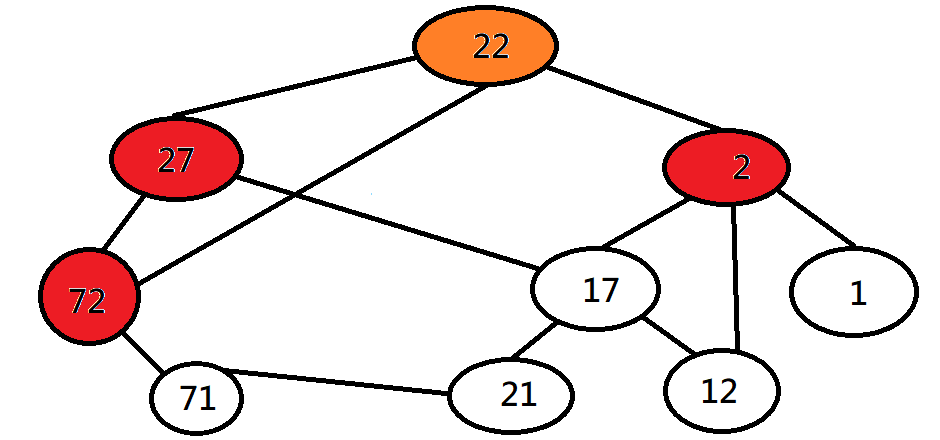
一層一層搜尋下去
寬度優先探訪 BFS
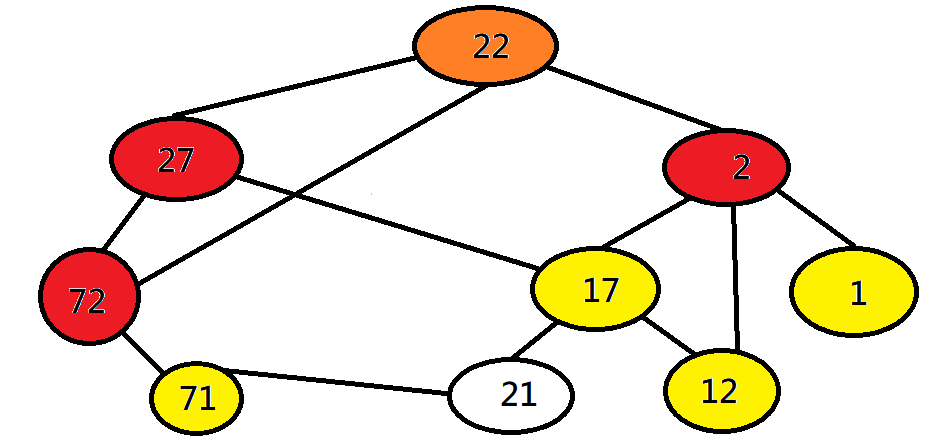
一層一層搜尋下去
寬度優先探訪 BFS
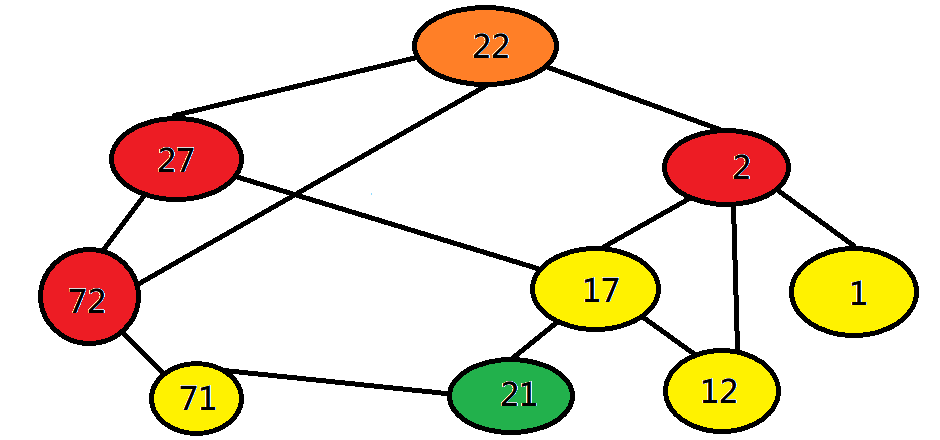
一層一層搜尋下去
寬度優先探訪 BFS
vector<int> v[N];
bool visited[N];
queue<int> q;
q.push(1);
visited[1] = 1;
while (q.size()) {
int u = q.front();
q.pop();
for (auto i:v[u]) if (!visited[i]) {
visited[i] = 1;
q.push(i);
}
}例題演練
Fire In The Forest
Fire In The Forest
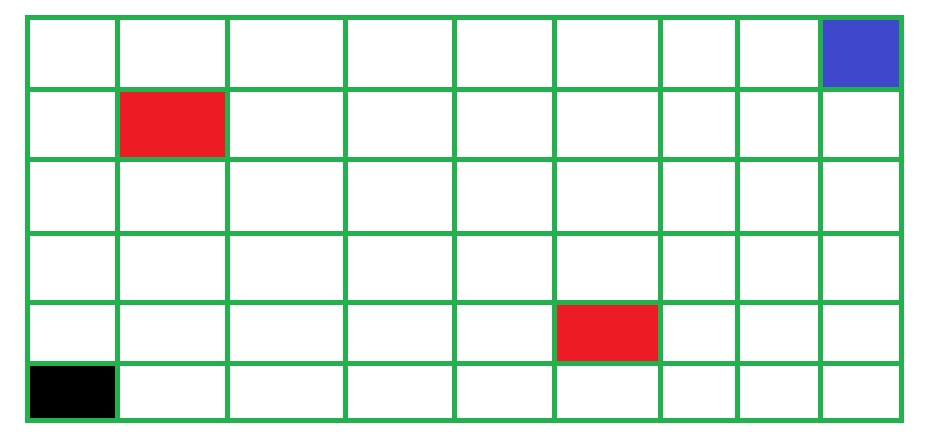
藍色是起點、黑色是目標、紅色是大火
Fire In The Forest
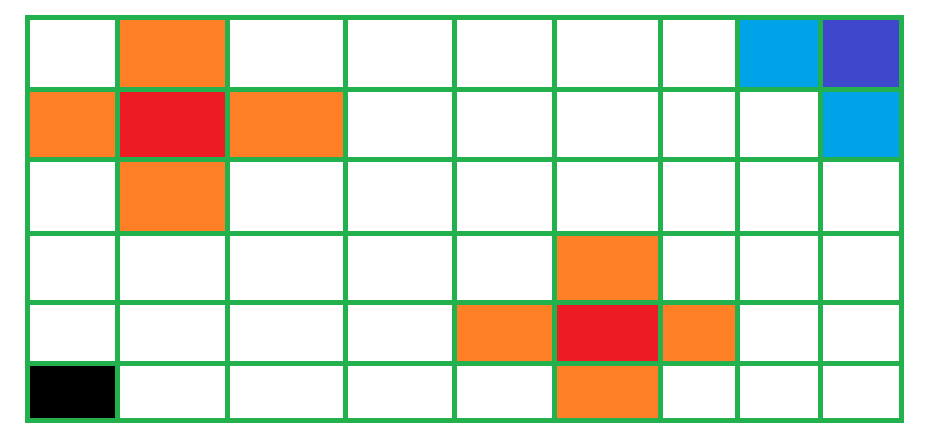
一秒後,森林的情況
Fire In The Forest
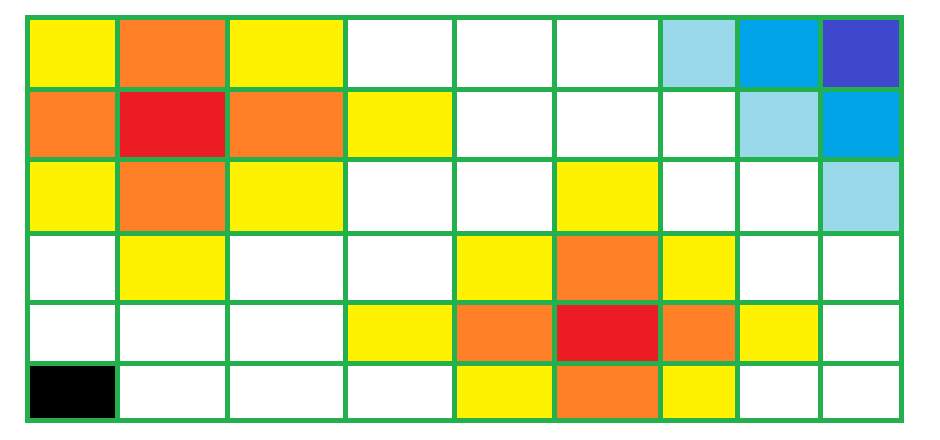
兩秒後,森林的情況
Fire In The Forest
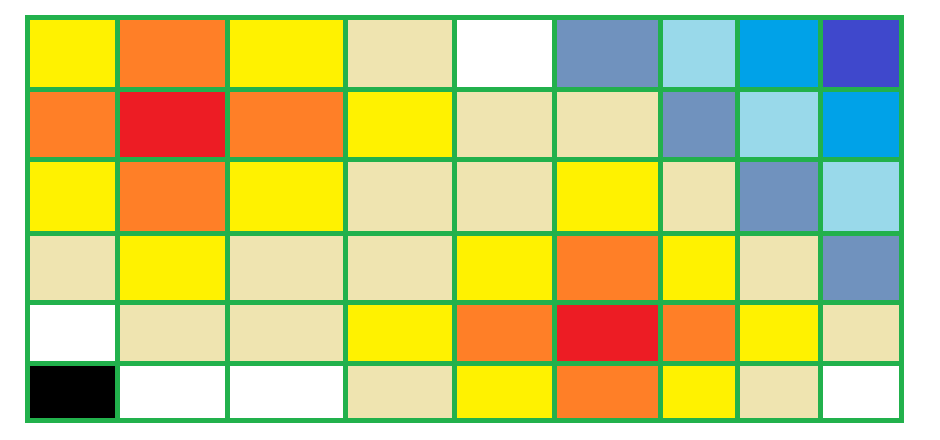
三秒後,森林的情況
Fire In The Forest
四秒後,森林的情況,好像有點花QAQ
Fire In The Forest

四秒後,森林的情況
Fire In The Forest

維護的是「人在第T秒可以走到的地方」與
「火在第T秒會燒到的地方」
火先燒,人再走=>火先放進Queue再放人
最短路徑
如果你從清大校門口到這裡繞了很大一圈
那你可能需要上這堂課......
邊權為一的圖

如何求 22 到其他點的最短路徑呢?
邊權為一的圖

如何求 22 到其他點的最短路徑呢?
邊權為一的圖

如何求 22 到其他點的最短路徑呢?
邊權為一的圖

如何求 22 到其他點的最短路徑呢?
邊權為一的圖

如何求 22 到其他點的最短路徑呢?
邊權為一的圖
int dis[N];
queue<int> q;
q.push(1);
dis[1] = 0;
visited[1] = 1;
while (q.size()) {
int u = q.front();
q.pop();
for (auto i:v[u]) if (!visited[i]) {
visited[i] = 1;
dis[i] = dis[u] + 1;
q.push(i);
}
}邊權為一?
邊權唯一
邊權唯一(假設是X)的圖
int dis[N];
queue<int> q;
q.push(1);
dis[1] = 0;
visited[1] = 1;
while (q.size()) {
int u = q.top();
q.pop();
for (auto i:v[u]) if (!visited[i]) {
visited[i] = 1;
dis[i] = dis[u] + x;
q.push(i);
}
}延伸討論
如果邊權只有 1 和 0 呢?
鬆弛
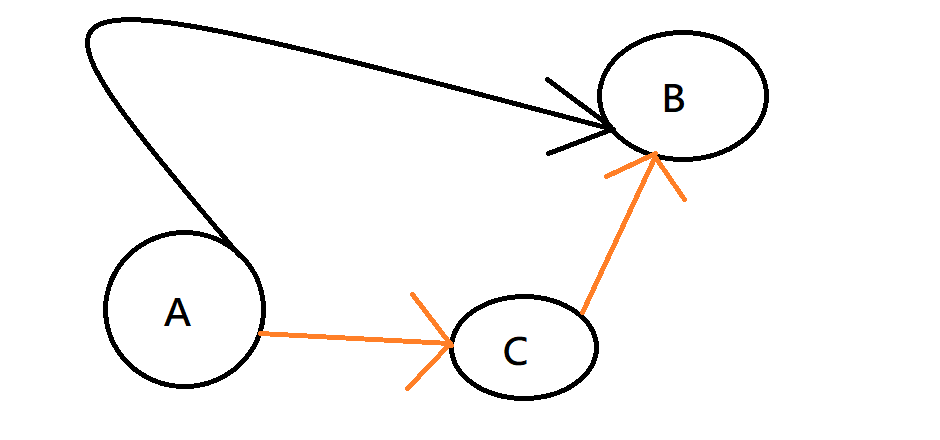
這條路太遠的話,就嘗試其他路
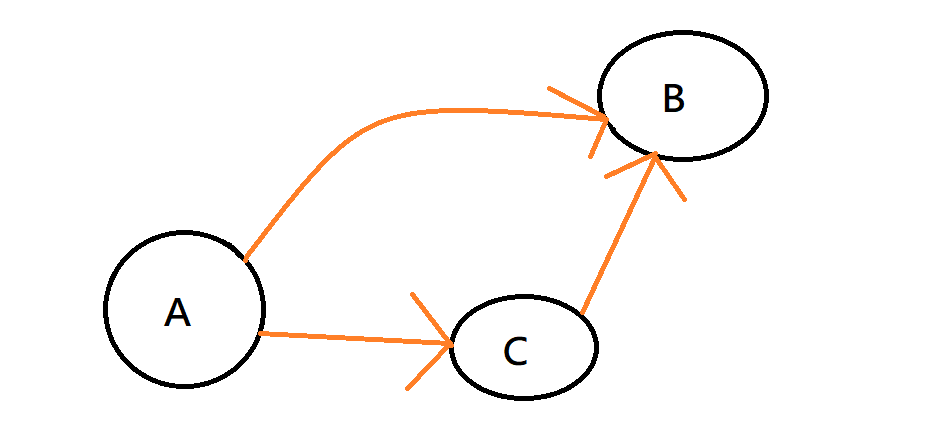
Dijkstra
不斷找最近的點,加進來,然後鬆弛其它點
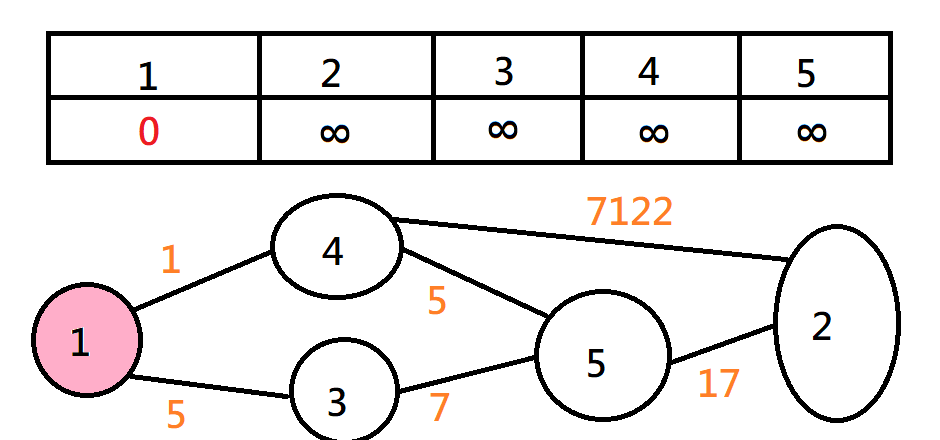
Dijkstra
不斷找最近的點,加進來,然後鬆弛其它點
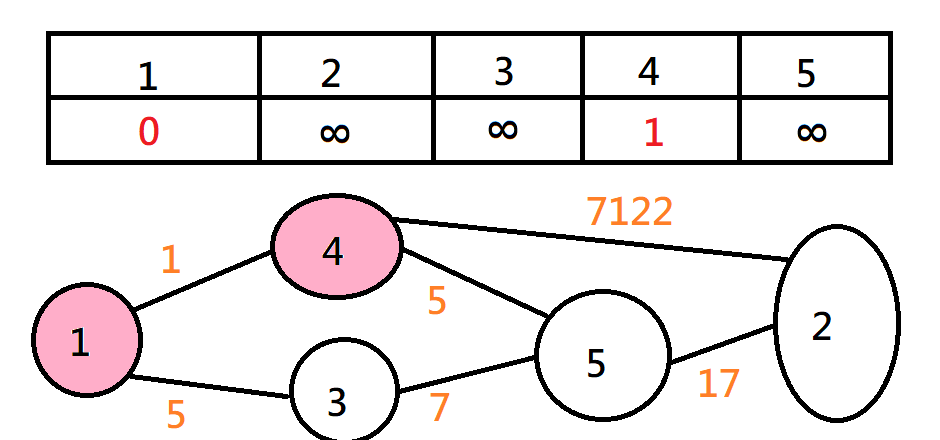
Dijkstra
不斷找最近的點,加進來,然後鬆弛其它點
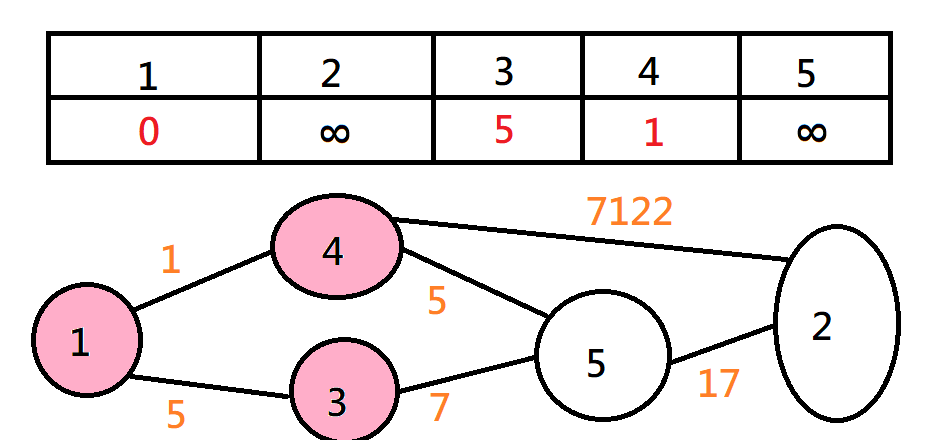
Dijkstra
不斷找最近的點,加進來,然後鬆弛其它點
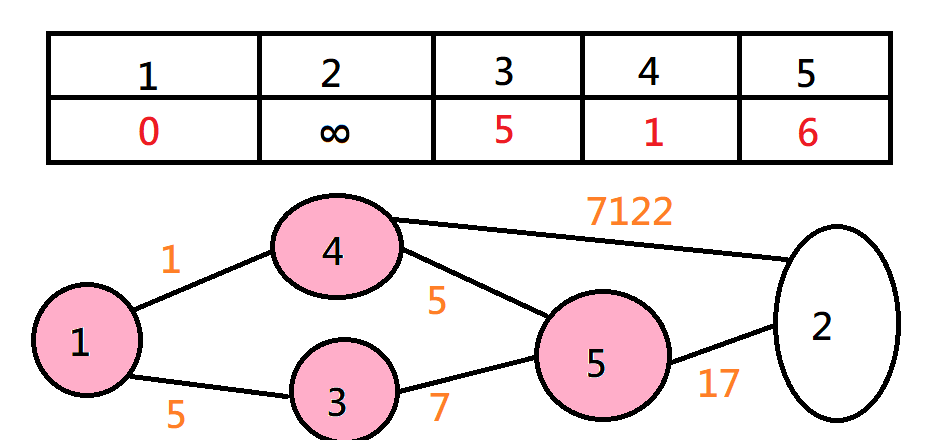
Dijkstra
不斷找最近的點,加進來,然後鬆弛其它點
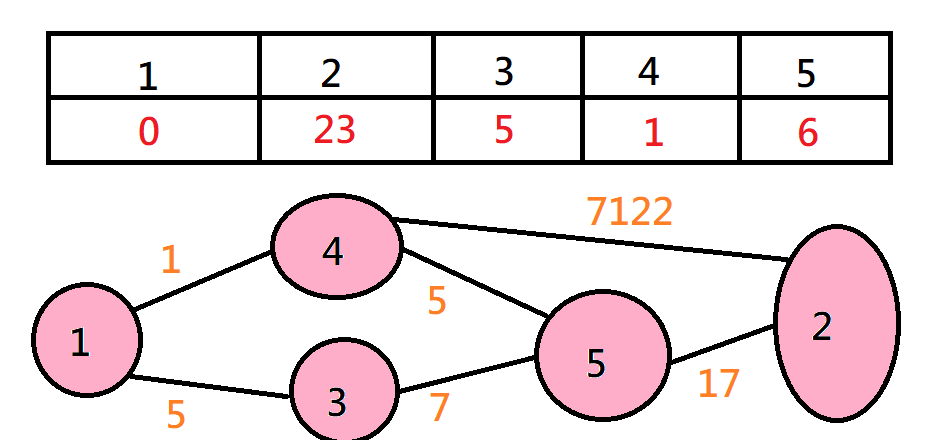
Dijkstra
所有已經加進來的點都不會再變小

Dijkstra
#define mk make_pair
using pi = pair<int,int>;
priority_queue<pi, vector<pi>, greater<pi>> pq;
for (int i = 2; i <= n; ++i) d[i] = 1e9;
pq.push(mk(0, 1)); //
while( pq.size() ) {
pi u = pq.top();
pq.pop();
if (d[u.second] != u.first) continue;
for (auto i:v[u.second]) {
if (d[i.first] > u.first + i.second) {
d[i.first] = u.first + i.second;
pq.push(mk( d[i.first], i.first ));
}
}
}負環呢?
只要一直走負環就會越來越小
Dijkstra
有負環的情況
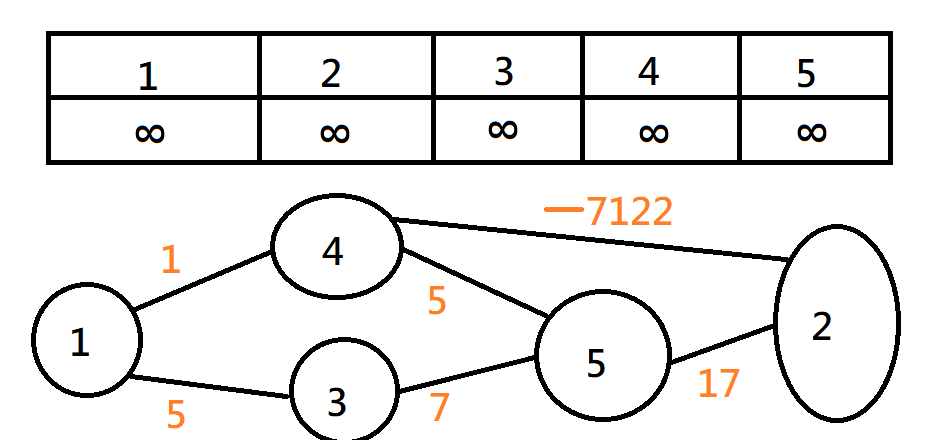
Dijkstra
有負環的情況
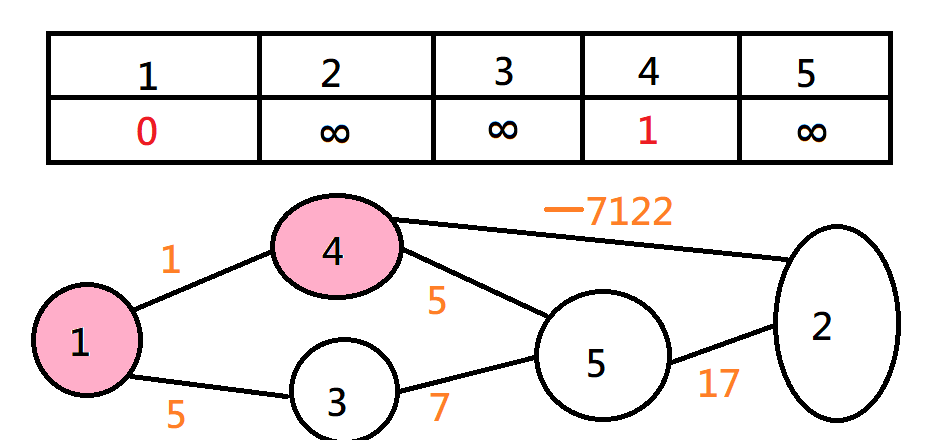
Dijkstra
有負環的情況
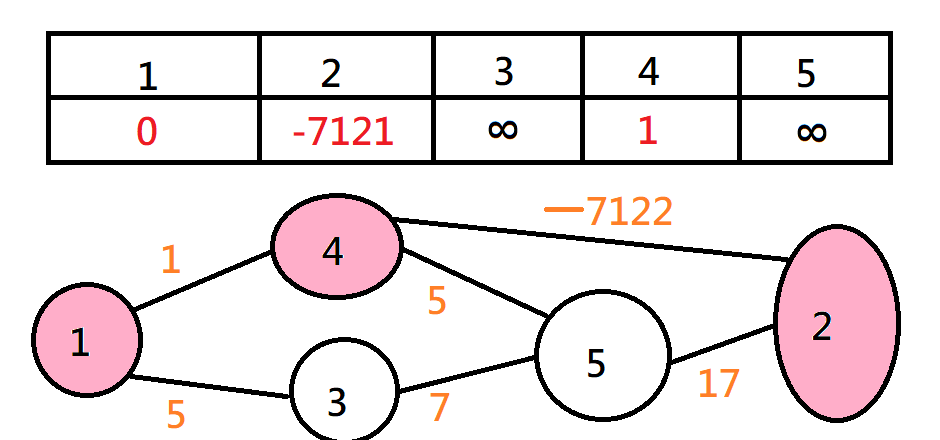
Dijkstra
有負環的情況
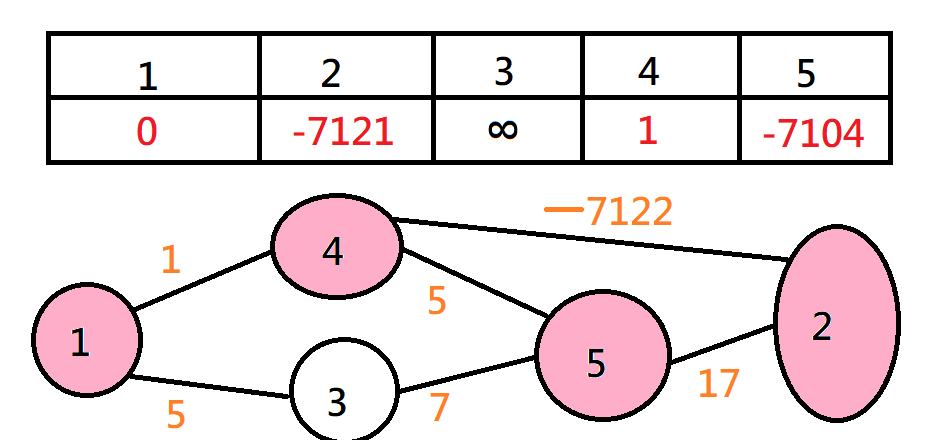
Dijkstra
有負環的情況
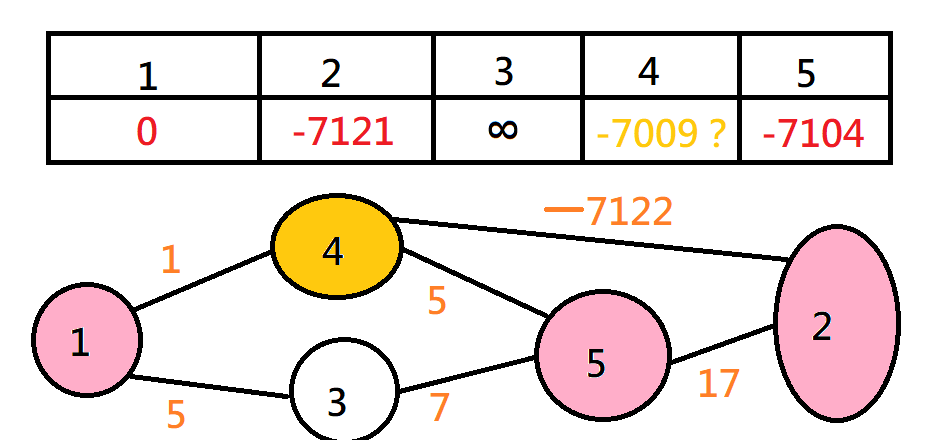
如果有負邊的話就不能將走過的點視為不會再被鬆弛的點
Bellmen-Ford
有負環的情況
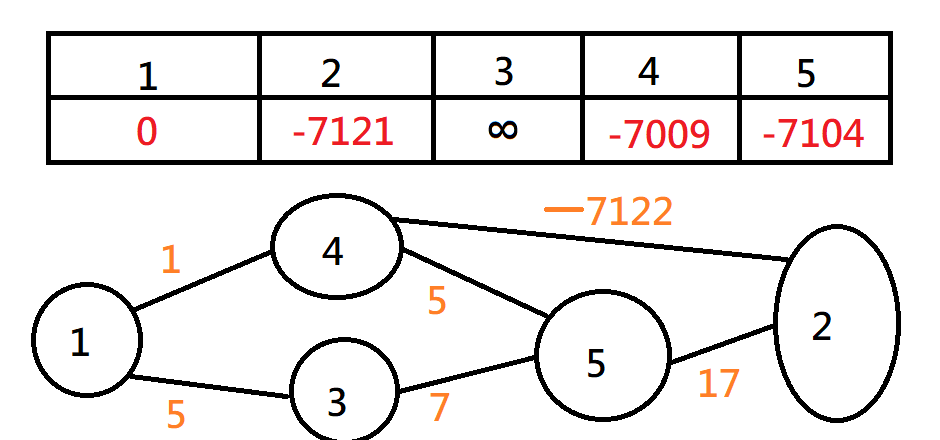
Bellmen-Ford
bool inque[N];
queue<int> q;
q.push(1);
inque[1] = 1;
while( q.size() ) {
int u = q.front();
q.pop();
inque[u] = 0;
for (auto i:v[u]) if ( d[i.first] > d[u] + i.second ) {
d[i.first] = d[u] + i.second;
if ( !inque[i.first] ) {
inque[i.first] = 1;
q.push(i.first);
}
}
}要如何知道有沒有負環?
1. 題目會給
2. Bellmen-Ford
Bellmen-Ford
一個點最多被更新幾次?

Bellmen-Ford
一個點最多被更新幾次?
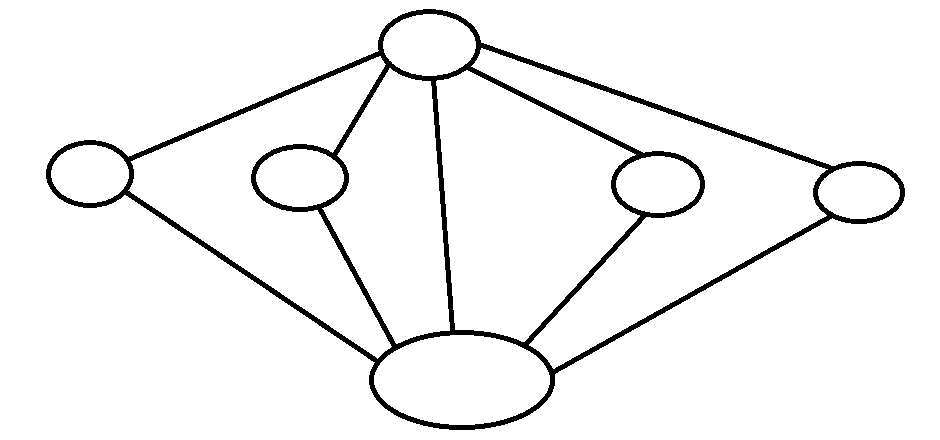
Bellmen-Ford
被同一個點重複更新的話,就有負環
因此最多被更新(V-1)次

Bellmen-Ford(SPFA)
int cnt[N];
bool SPFA() {
while( q.size() ) {
int u = q.front();
q.pop();
inque[u] = 0;
for (auto i:v[u]) if ( d[i.first] > d[u] + i.second ) {
if ( ++cnt[i.first] >= n ) return false;
d[i.first] = d[u] + i.second;
if ( !inque[i.first] ) {
inque[i.first] = 1;
q.push(i.first);
}
}
return true;
}
}
有沒有辦法一次求出任兩點的距離?
鬆弛

這條路太遠的話,就嘗試其他路

鬆弛

主動嘗試用C去鬆弛AB

鬆弛
主動嘗試用1, 2, 3, 4, 5去鬆弛所有路徑

dp[ a ][ b ] =
min(dp[ a ][ b ], dp[ a ][ c ] + dp[ c ][ b ]
Floyd-Warshall
按照順序,由一個點一個點嘗試去鬆弛所有路徑
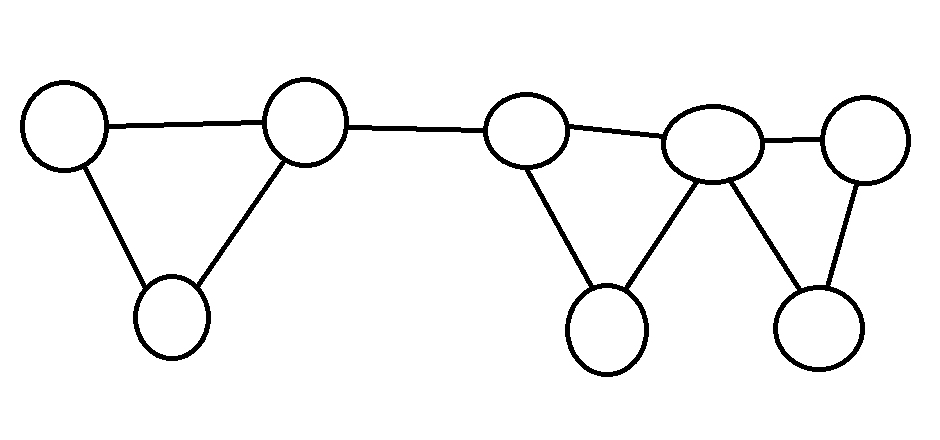
Floyd-Warshall
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j) {
if (G[i][j] == 0) dp[i][j] = 1e9;
else dp[i][j] = G[i][j];
}
for (int k = 1; k <= n; ++k)
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
dp[i][j] = min(
dp[i][j],
dp[i][k] + dp[k][j]
);問每個點是否在負環上?
自己到自己的距離為無限大
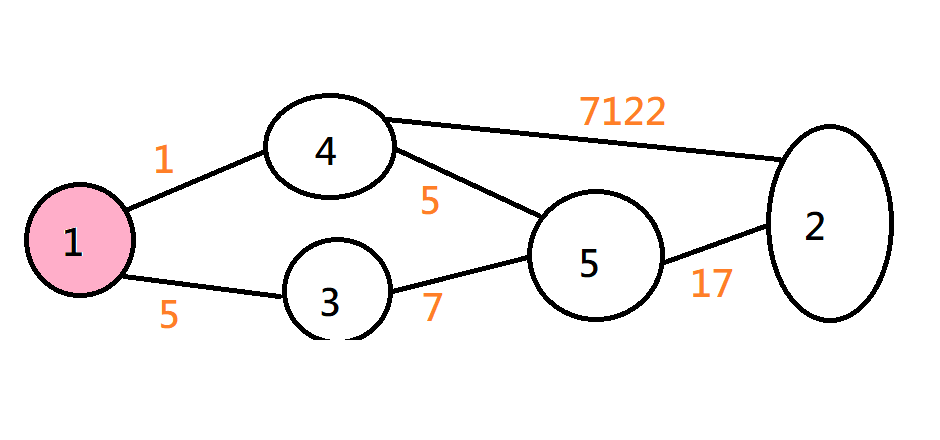
問每個點是否在負環上?
經過Floyd-Warshall後,自己可以由一個路徑走到自己

找環(二)?
我只想知道 2 號點是否有環經過?

不定向邊1290
給定一張邊數和點數都少於10^6的圖
每條邊都有權重,且皆為非負整數
並給定起點與終點
請問在可以自由決定每條邊的方向的情況下
最短路徑為何?
不定向邊1290
Dijkstra

樹
多種樹,環保愛地球
根
根沒有父節點
又或者根的父節點就是自己......
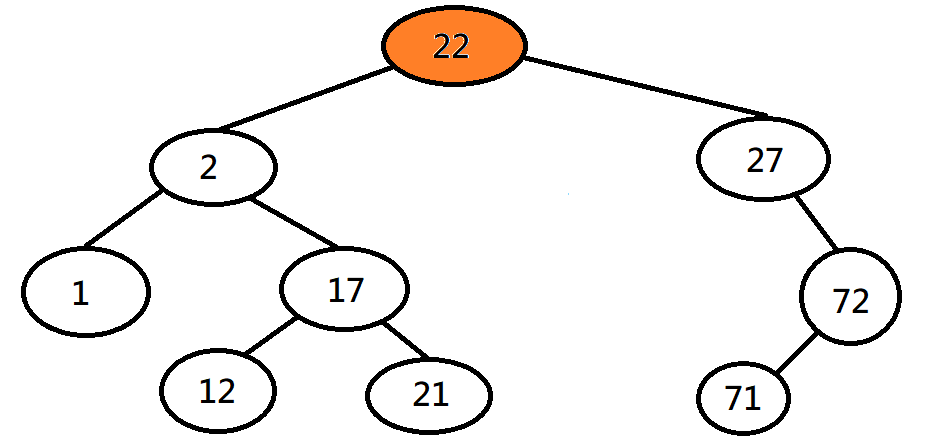
子節點
根的子節點的父節點是自己
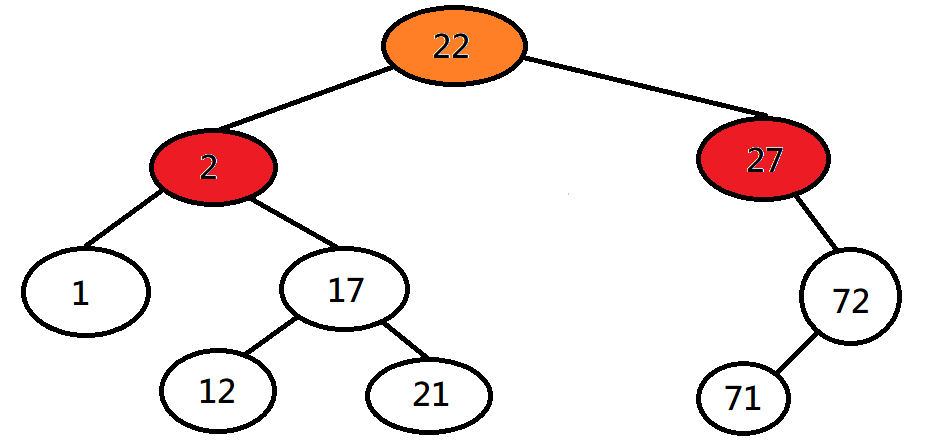
葉節點
沒有子節點的節點
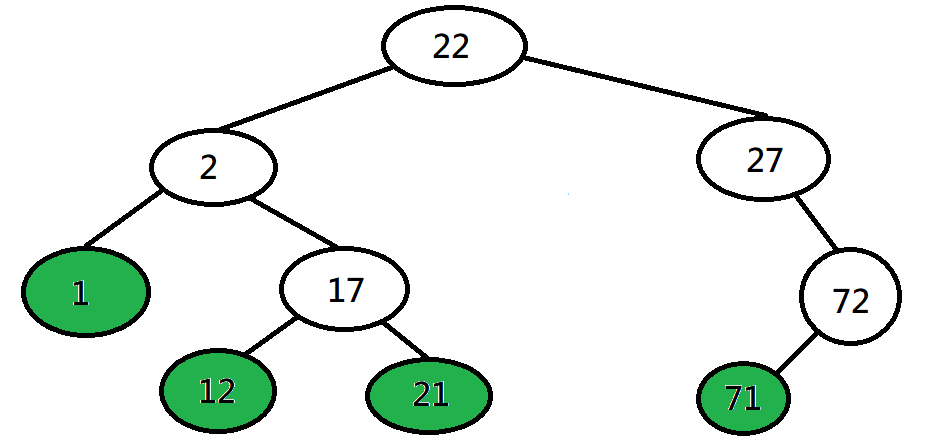
樹的性質
- 剛好有V - 1條邊
- 樹上沒有環,任意加一條邊都會造成環
- 此樹連通,拿掉任何一條邊都會不連通
- 任兩點有唯一一條路徑
二元樹
每個節點的子節點最多只有兩個
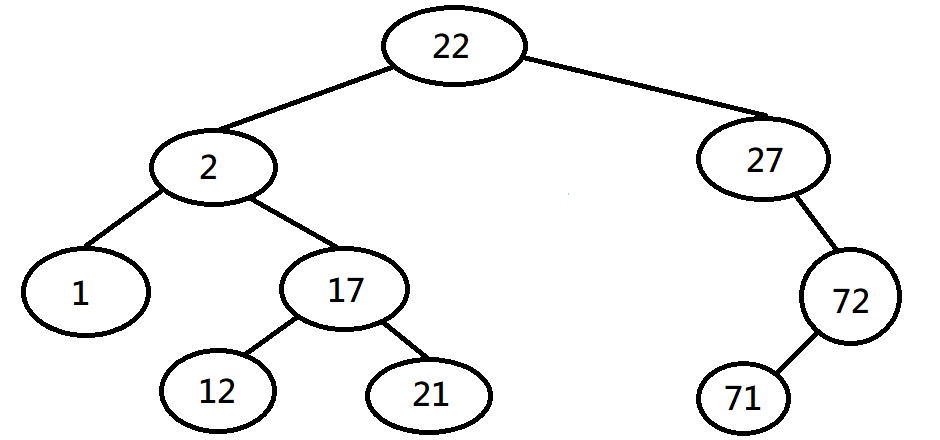
非二元樹
有些節點的子節點超過兩個
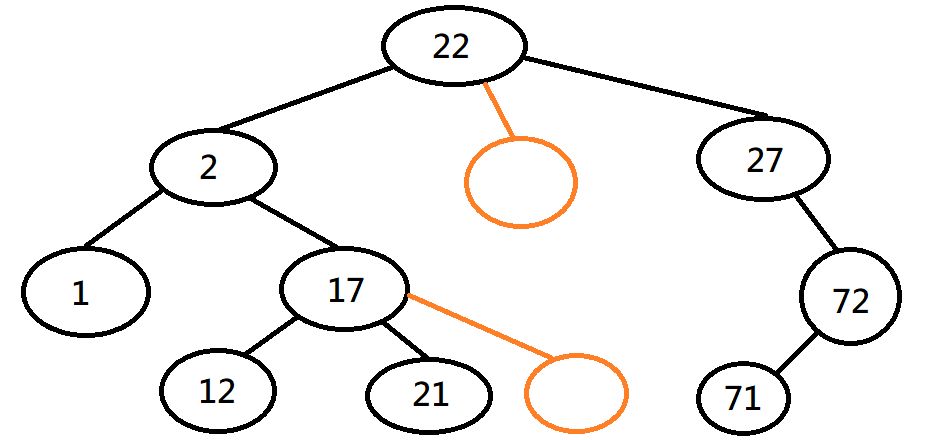
二元樹的遍歷
前序:先走根、再走左子樹
紅橙黃綠藍靛紫黑白
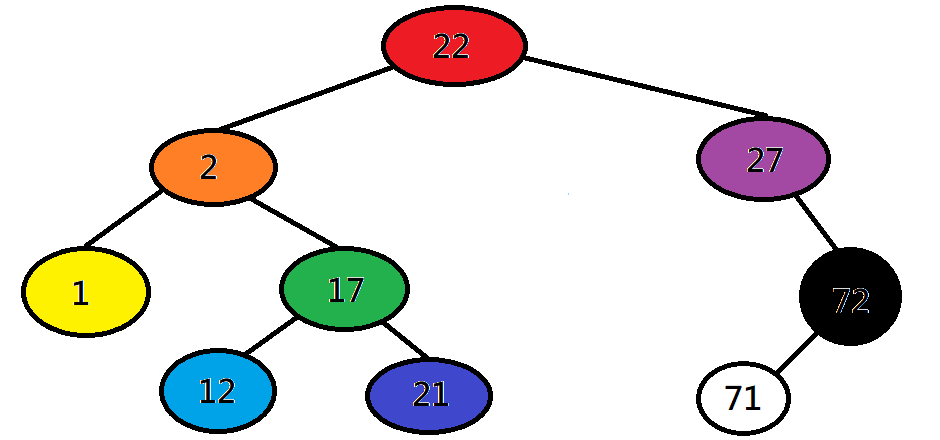
二元樹的遍歷
前序:先走根、再走左子樹
紅橙黃綠藍靛紫黑白
void dfs(int x, int p) {
cout << x << endl;
dfs(l[x], x);
dfs(r[x], x);
}二元樹的遍歷
中序:先走左子樹、再走根
紅橙黃綠藍靛紫黑白
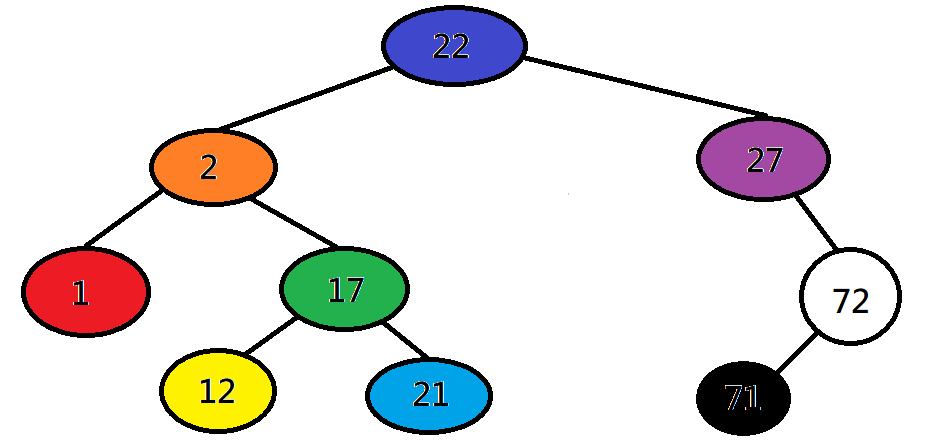
二元樹的遍歷
中序:先走左子樹、再走根
紅橙黃綠藍靛紫黑白
void dfs(int x, int p) {
dfs(l[x], x);
cout << x << endl;
dfs(r[x], x);
}二元樹的遍歷
後序:先走左子樹、再走右子樹、最後走根
紅橙黃綠藍靛紫黑白
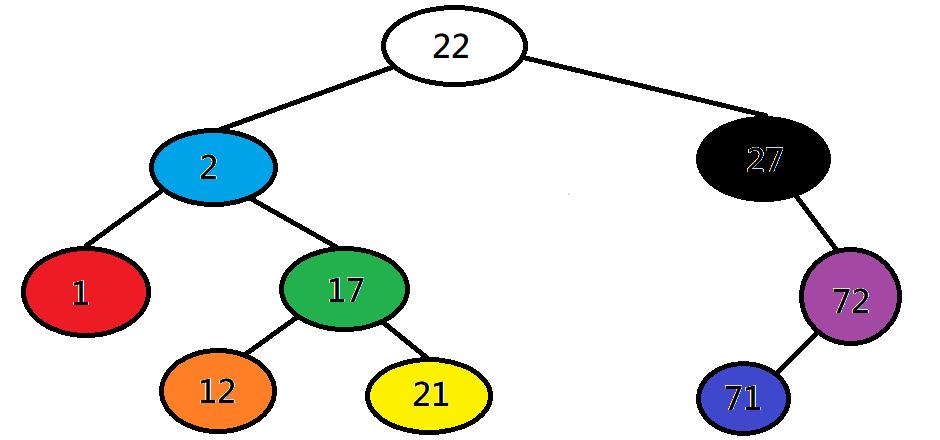
二元樹的遍歷
後序:先走左子樹、再走右子樹、最後走根
紅橙黃綠藍靛紫黑白
void dfs(int x, int p) {
dfs(l[x], x);
dfs(r[x], x);
cout << x << endl;
}二元樹的遍歷
層次:由左至右、由上至下
紅橙黃綠藍靛紫黑白
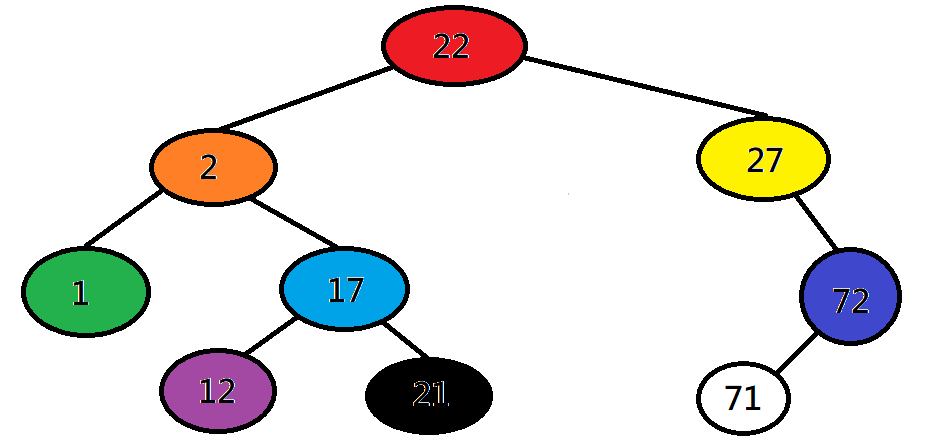
二元樹的遍歷
層次:由左至右、由上至下
紅橙黃綠藍靛紫黑白
queue<int> q;
q.push(1);
while(q.size()) {
int u = q.front();
q.pop();
cout << u << endl;
q.push(l[u]);
q.push(r[u]);
}Binary Full Tree
完滿二元樹:所有節點都有兩個子節點
除了葉節點以外
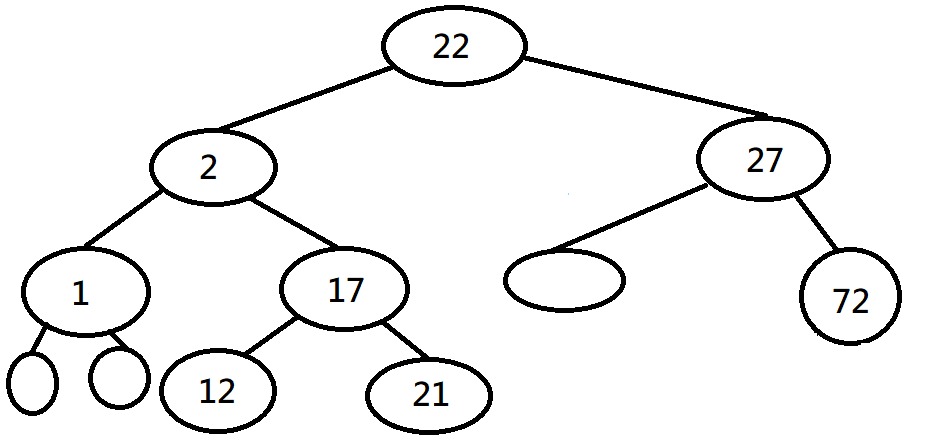
Complete Binary Tree
完整二元樹:由上至下、由左至右塞滿
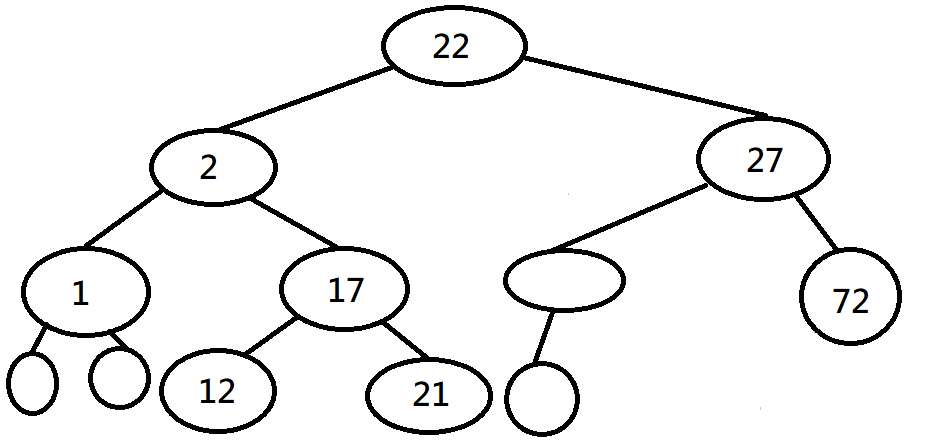
比較
完滿二元樹不一定是完整二元樹
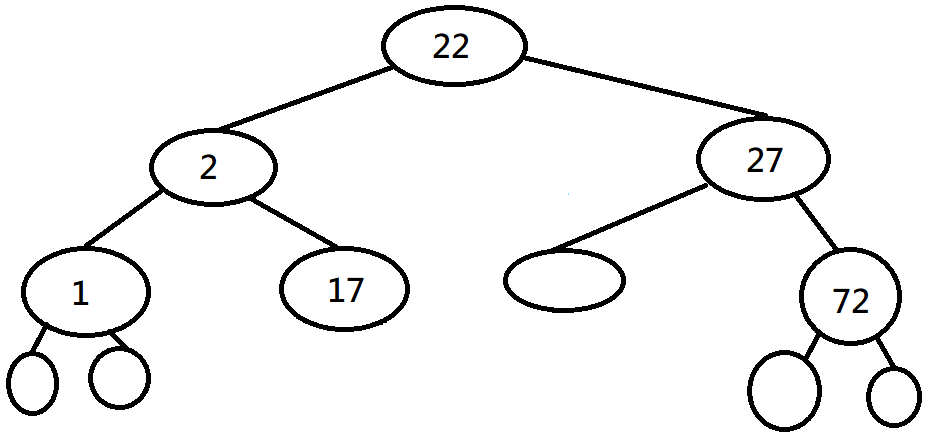
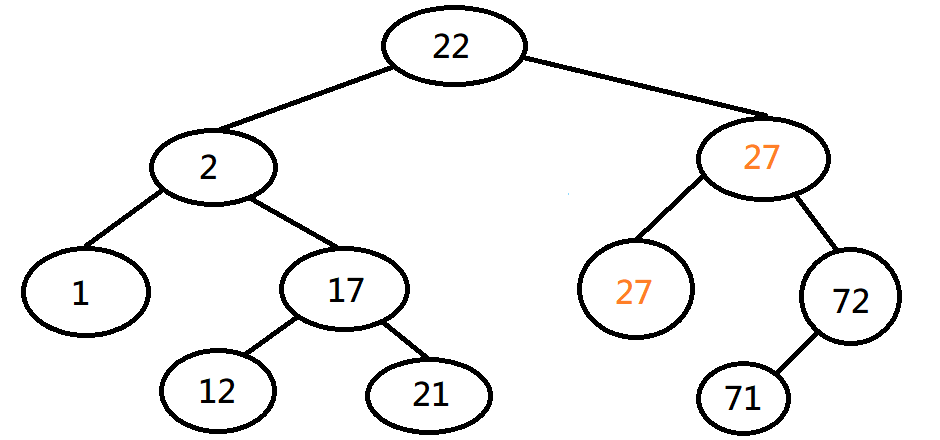
二元搜尋樹
現在有一顆空的二元搜尋樹
並按照順序插入一些數字
最後請輸出這棵樹的中序表示法
請大家以下列數列試試看

22, 27, 1, 2, 17, 12, 21, 72, 71
二元搜尋樹
排序後輸出
cin >> input;
sort(input.begin(), input.end());
cout << input;最小生成樹 MST
在充滿汙染的世界中,尋找樹

from 德羅布狐狸-迷因大盜
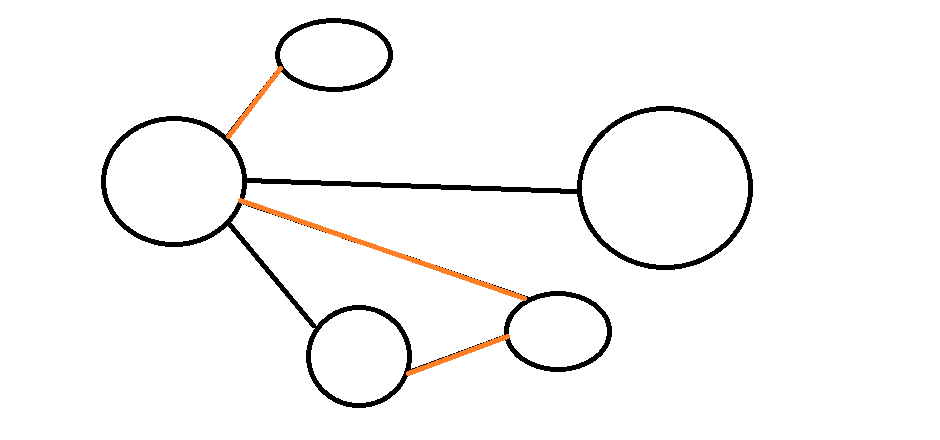
最小生成樹 MST
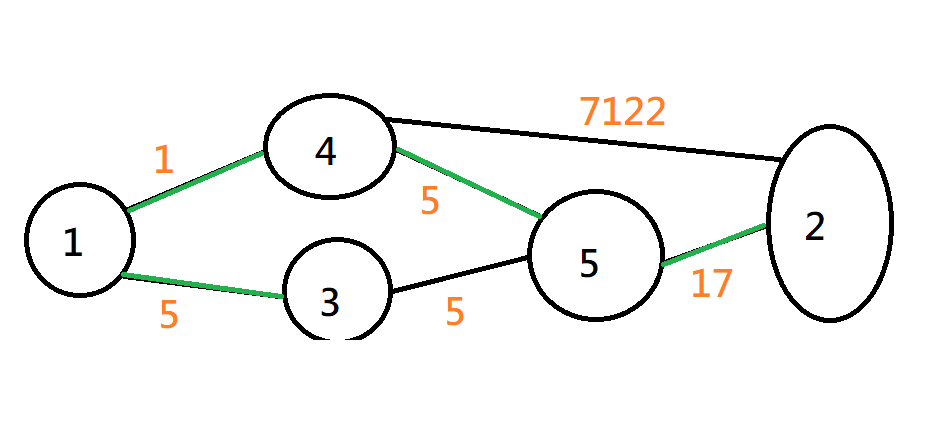
一個最小生成樹的例子
Kruskal
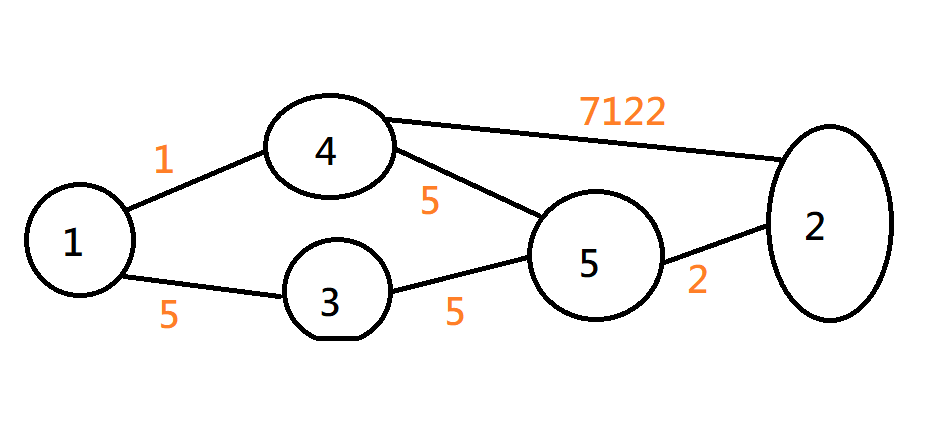
將邊按照邊權由小到大排序
Kruskal
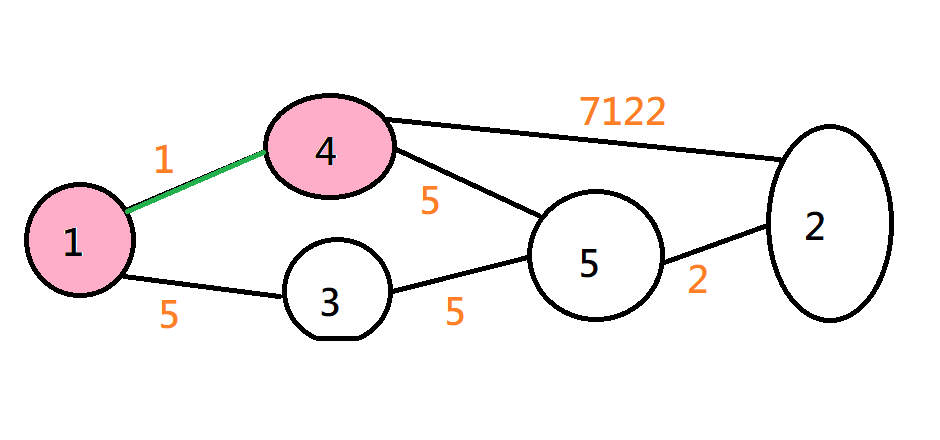
從小到大一條邊一條邊加進來
Kruskal
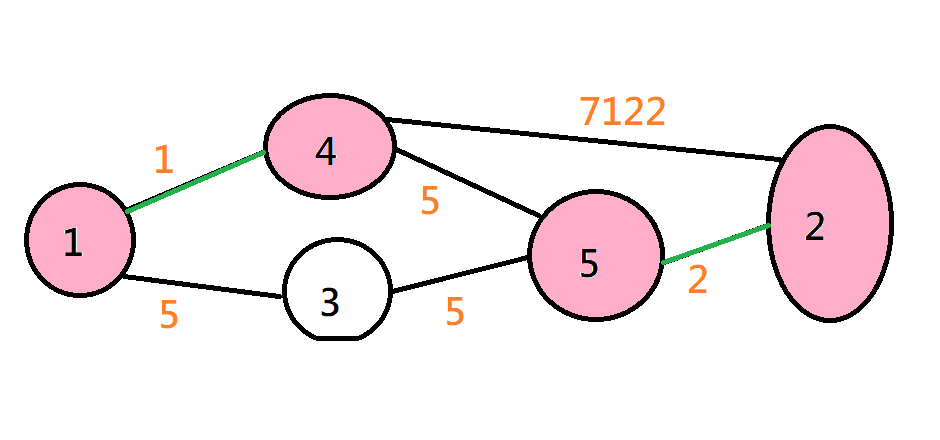
從小到大一條邊一條邊加進來
Kruskal
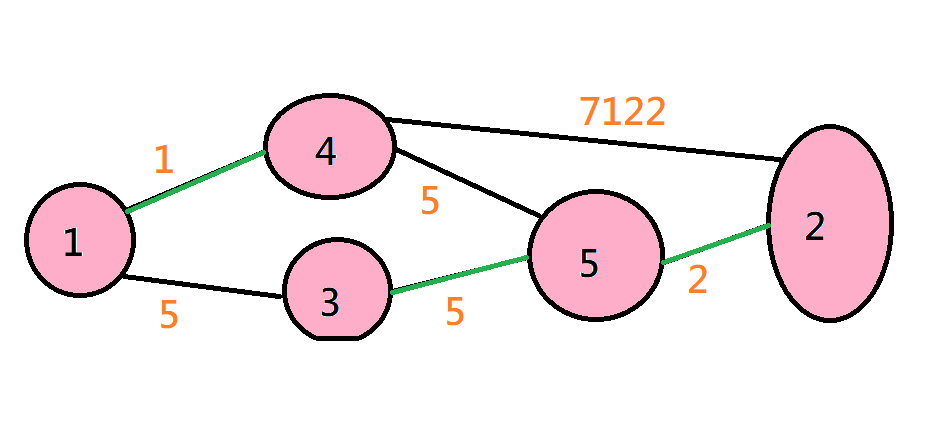
從小到大一條邊一條邊加進來
Kruskal
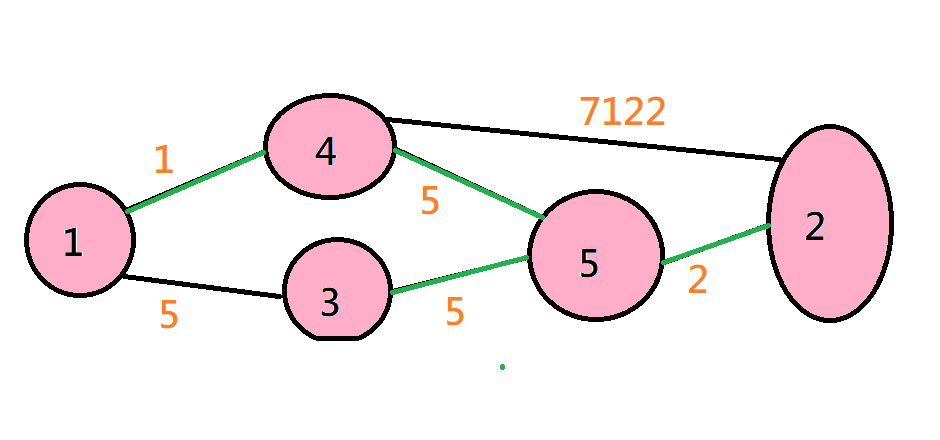
從小到大一條邊一條邊加進來
Kruskal
#define mk make_pair
#define F first
#define S second
vector<pair<int, pair<int,int>>>G;
for (int i = 1; i <= m; ++i) {
int a, b, w;
cin >> a >> b >> w;
G.pb(mk(w, mk(a, b)));
}
sort(G.begin(), G.end());
for (auto i:G) if (!same(i.S.F, i.S.S)) {
unite(i.S.F, i.S.S);
ans += i.F;
}Prim
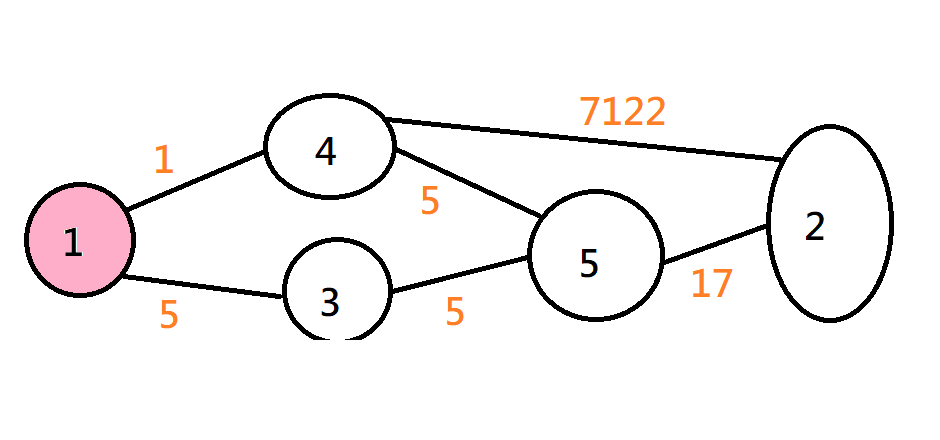
先隨便選一個點
(一個點也算一棵樹)
Prim
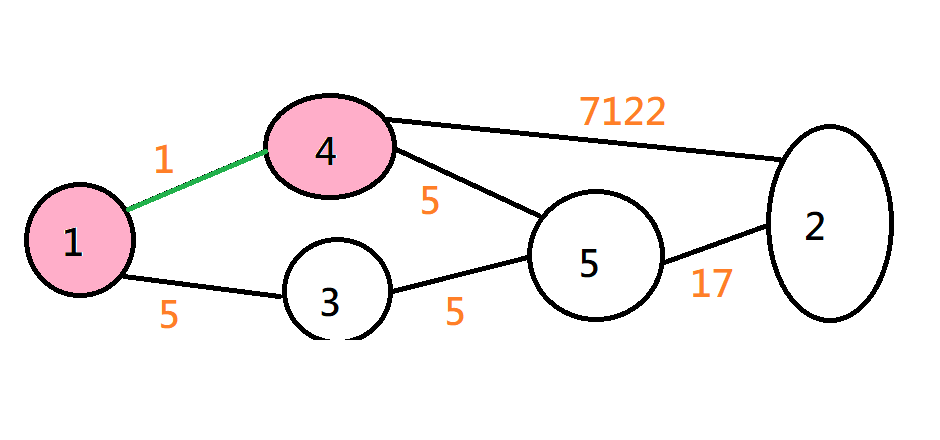
將離目前的生成樹最近的點加進來
Prim
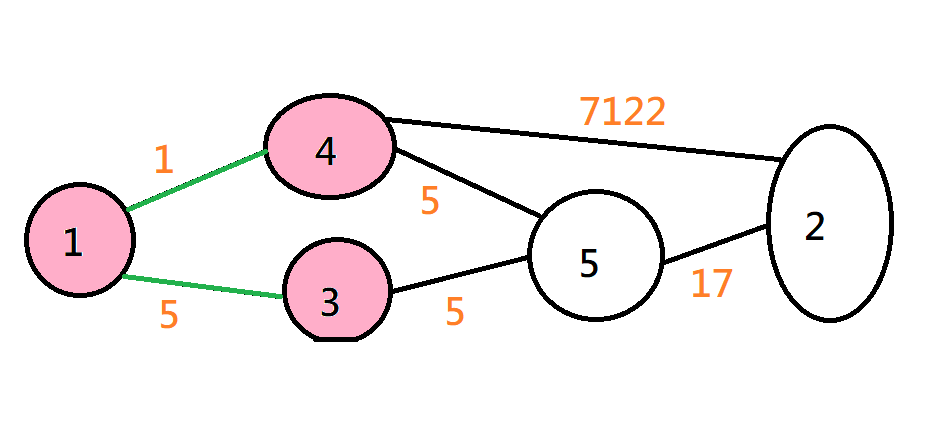
將離目前的生成樹最近的點加進來
Prim
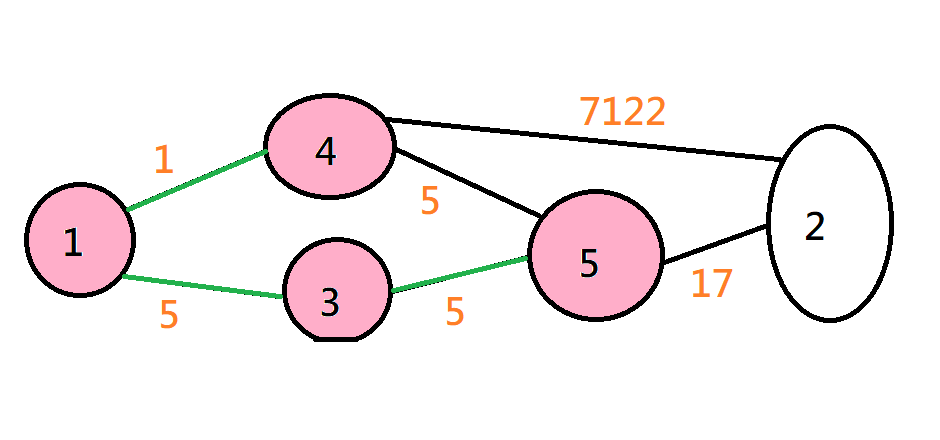
將離目前的生成樹最近的點加進來
Prim
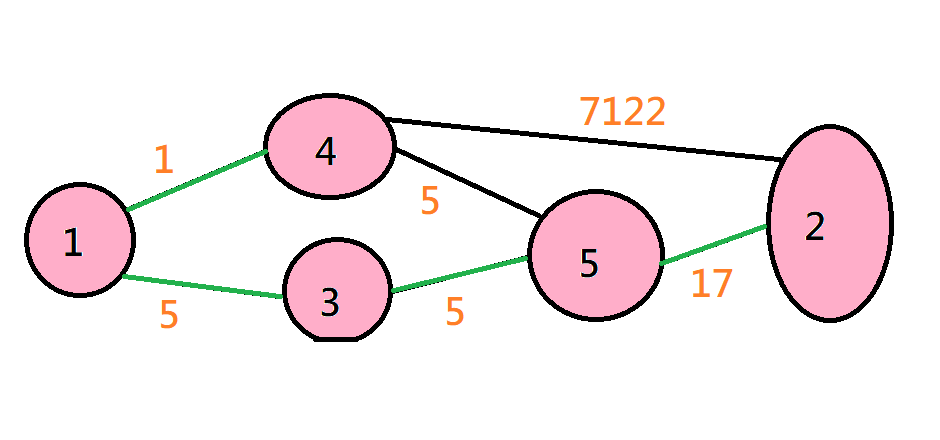
DONE
Prim
inline int prim() {
int ans = 0;
visited[1] = 1;
pq.push(make_pair(0, 1));
while (pq.size()) {
pi u = pq.top();
pq.pop();
if (visited[u.second]) continue;
visited[u.second] = 1;
ans += u.first;
for (auto i:v[u.second]) {
pq.push(i.second , i.first);
// second代 表 邊 權、 first代 表 連 到 的 點
}
}
return ans;
}
一張圖可能有很多棵不同的MST
一張圖,兩種MST


如何求出所有MST?
有點難,我們未來有機會再討論QAQ
如何判斷MST是否唯一?

Kruskal
同個連通塊裡有很多條權重一樣的邊可以被加入
如何判斷MST是否唯一?
int pre = -1;
int ok = 0;
for (auto i:G) {
if ( same(i.S.F, i.S.S) ) {
if (i.F == pre) ok = 1;
if (ok) break;
continue;
}
unite(i.S.F, i.S.S);
pre = i.F;
}咕嚕咕嚕呱呱呱呱
給你一張邊權是 1 或 0 的無向圖
請問它有沒有一棵權重大小剛好為 K 的生成樹
咕嚕咕嚕呱呱呱呱
最小生成樹
最大生成樹
有沒有等於 K 的生成樹?
拓撲排序
你爸爸的爸爸不可能是你的兒子

拓撲排序
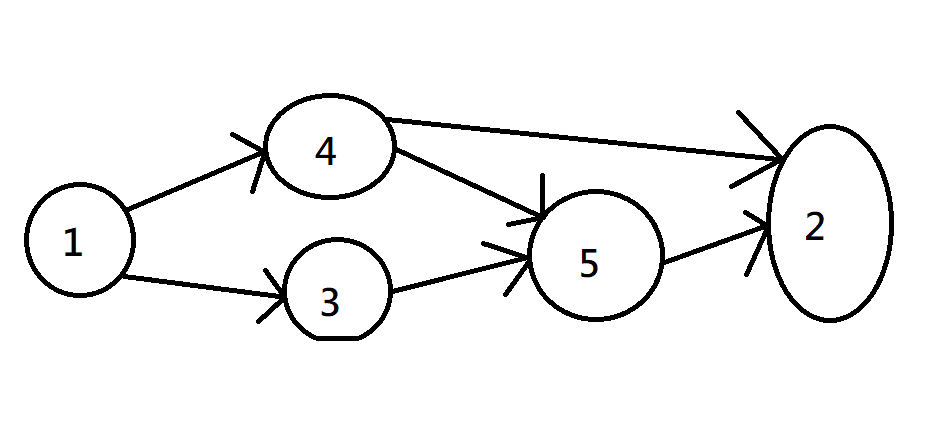
Directed Acyclic Graph(DAG)
有向無環圖
拓撲排序
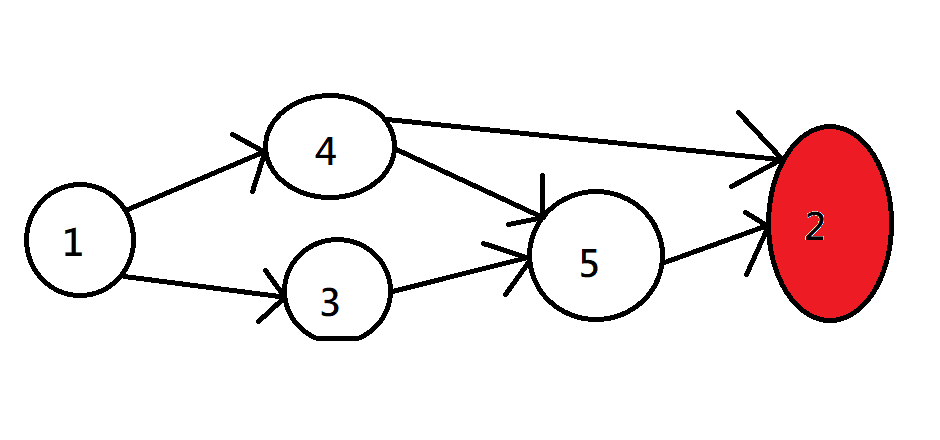
每次將出度為零的點push進序列
紅橙黃綠藍
拓撲排序
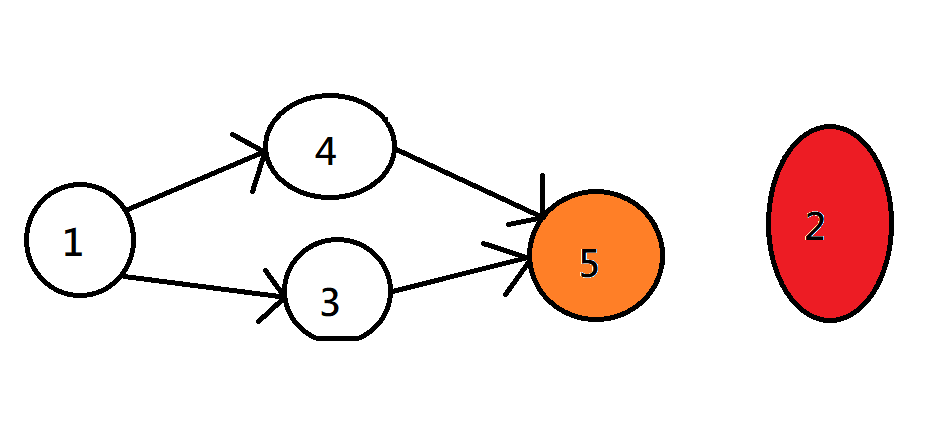
每次將出度為零的點push進序列
紅橙黃綠藍
拓撲排序
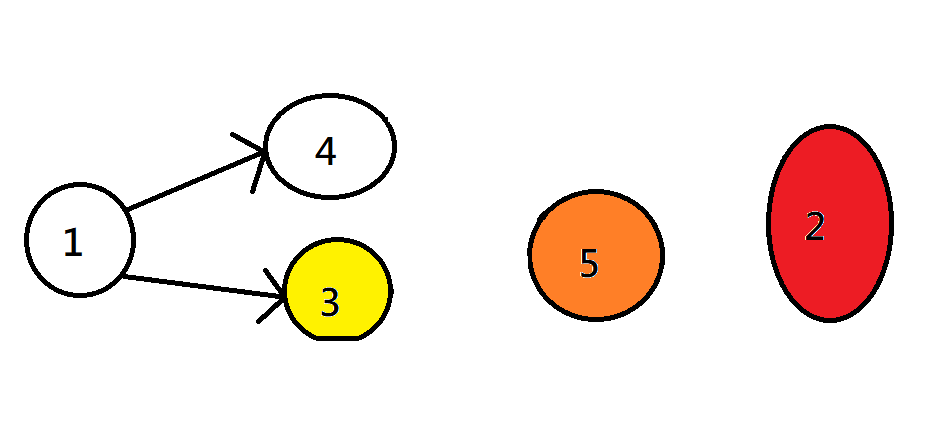
每次將出度為零的點push進序列
紅橙黃綠藍
拓撲排序
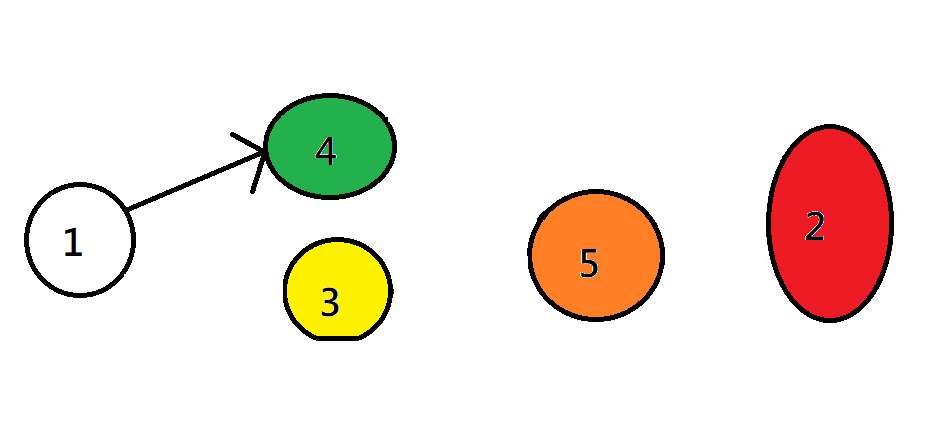
每次將出度為零的點push進序列
紅橙黃綠藍
拓撲排序
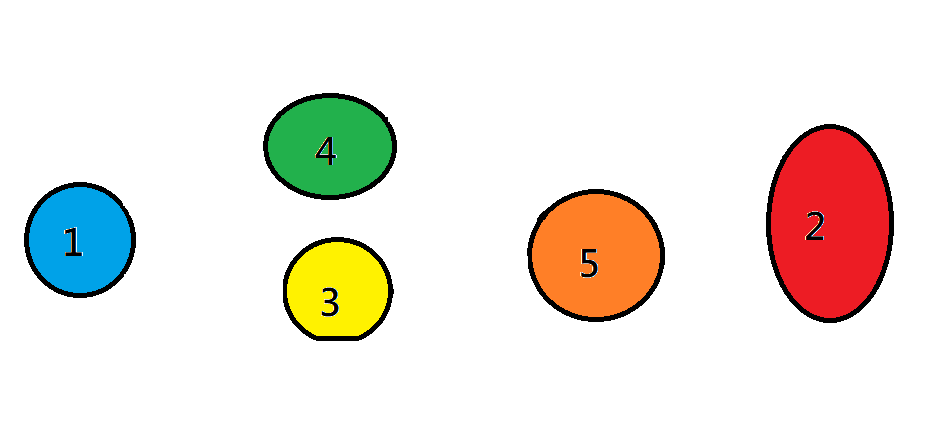
每次將出度為零的點push進序列
紅橙黃綠藍
拓撲排序
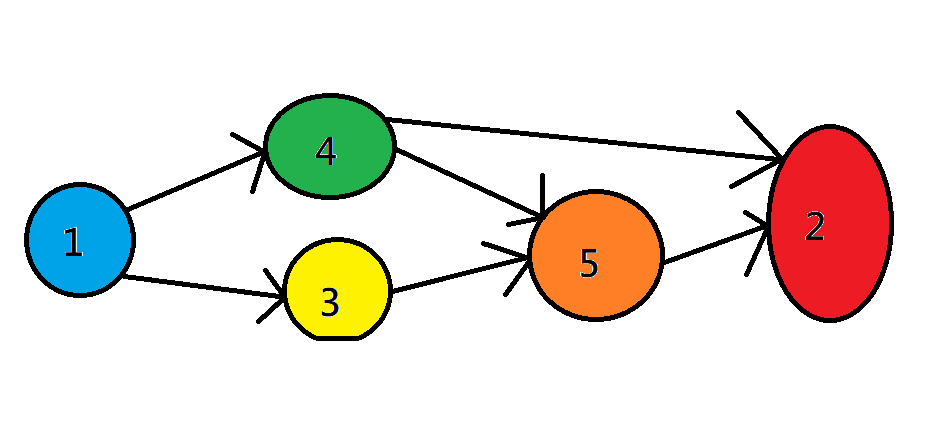
DONE
拓撲排序
int n, m, deg[1000009];
vector <int> s, ans, v[1000009], u[1000009];
//u是相反的邊
vector <int> TopologicalSort() {
for (int i = 1; i <= n; ++i) {
if (deg[i] == 0) s.push_back(i);
deg[i] = v[i].size();
}
while (s.size()) {
ans.push_back(s.back());
s.pop_back();
for (auto i:u[ans.back()]) {
deg[i]--;
if (!deg[i]) s.push_back(i);
}
}
return ans;
}二分圖
你知道嗎,火車和火車站之間竟然是二分圖的關係
Bipartite Graph二分圖
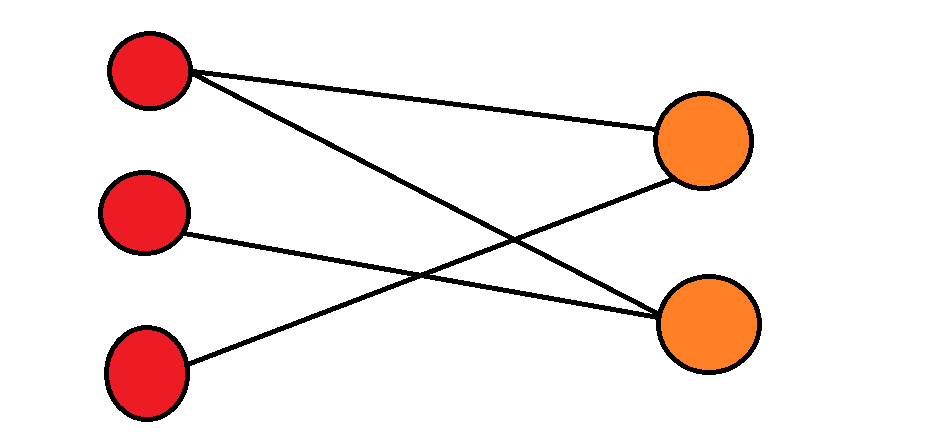
同一邊之間互相不連通
Bipartite Graph二分圖
偶環
Bipartite Graph二分圖

奇環
判斷二分圖
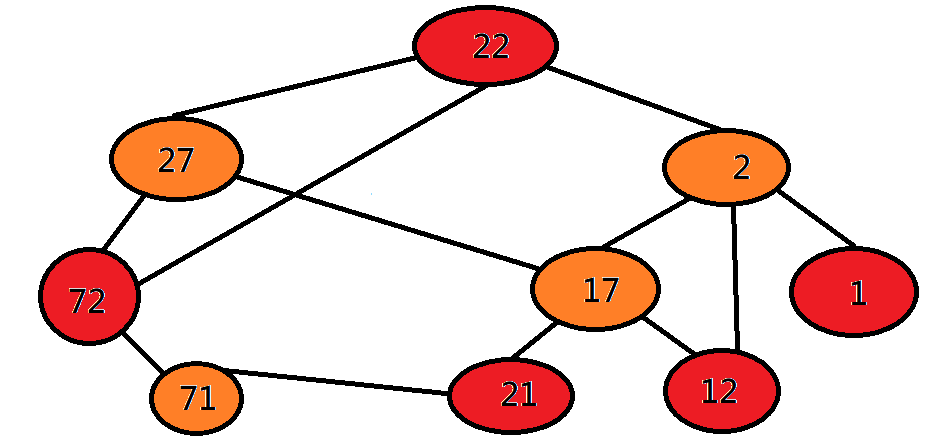
DFS
判斷二分圖
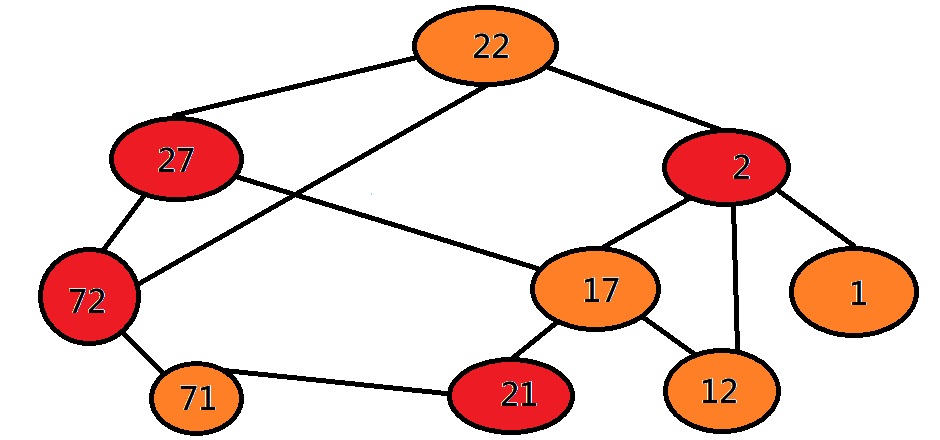
BFS
判斷二分圖
vector <int> v[1000009];
bitset <1000009> visited;
int col[1000009];
inline bool dfs(int x, int color) {
bool isBip = 1;
col[x] = color;
visited[x] = 1;
for (auto i:v[x]) {
if (visited[i] && col[i] == col[x]) return false;
if (!visited[i]) isBip &= dfs(i, color^1);
}
return isBip;
}所以火車與火車站和二分圖有甚麼關係?
那我/你和火車有甚麼共通點?

歐拉迴路
一座城市中,能否剛好走過每條路一次呢?
歐拉與柯尼斯堡
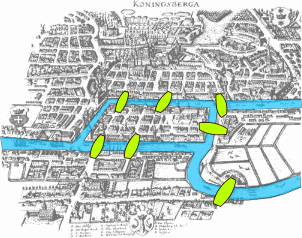
一筆畫問題
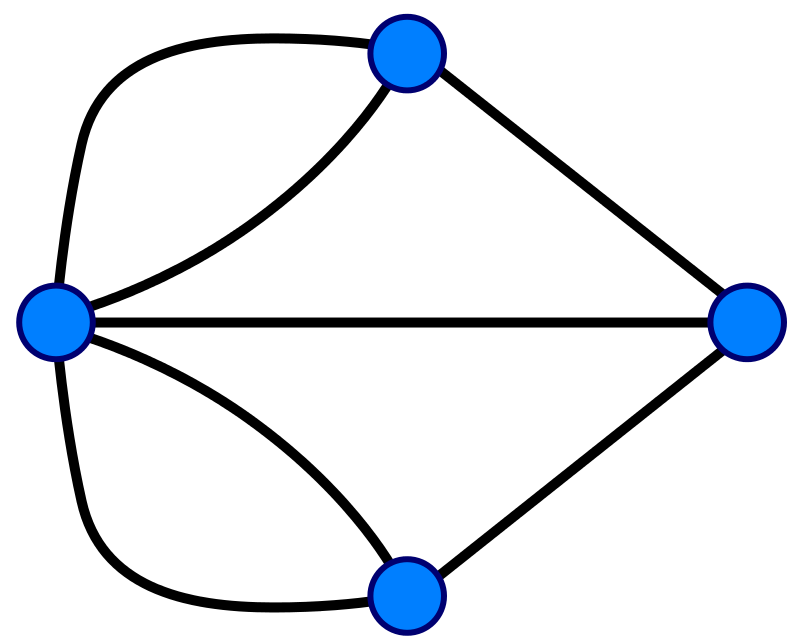
甚麼時候不會有一筆畫呢?
度數
一條邊貢獻的度數是二
一筆畫除了端點外的點都有一條邊進去一條邊出來
如果度數是奇數的點太多就......
除了端點以外的點的度數都是偶數
甚麼時候不會有一筆畫呢?
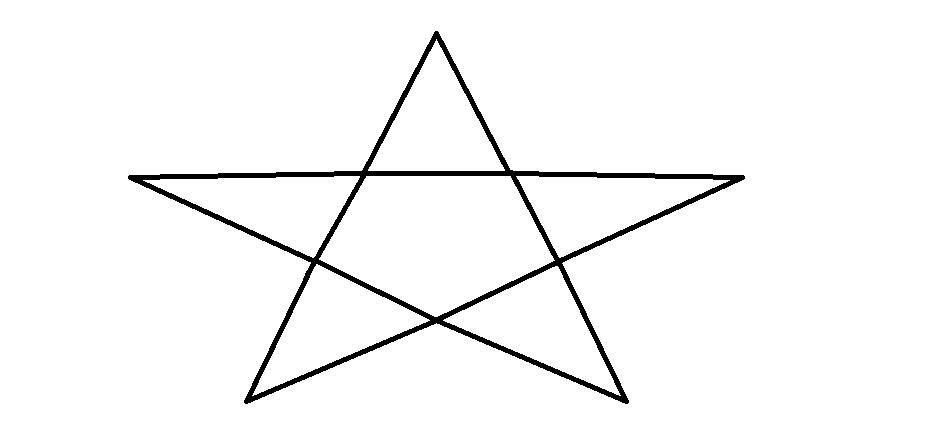
甚麼時候不會有一筆畫呢?
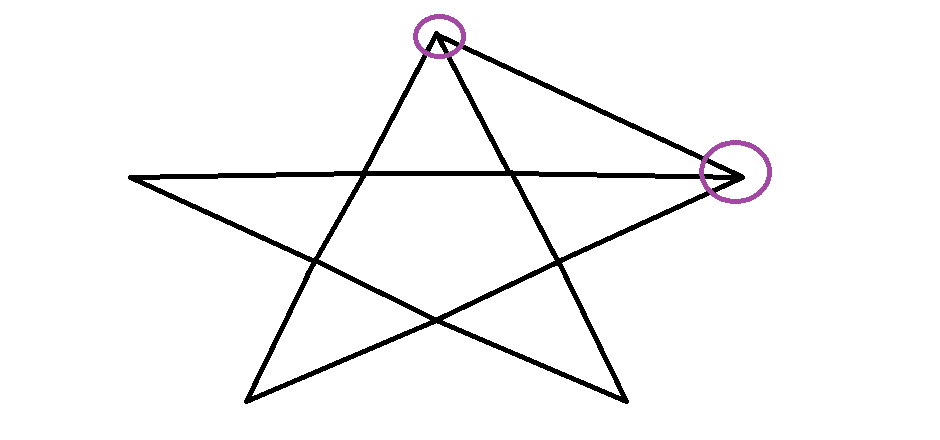
甚麼時候不會有一筆畫呢?
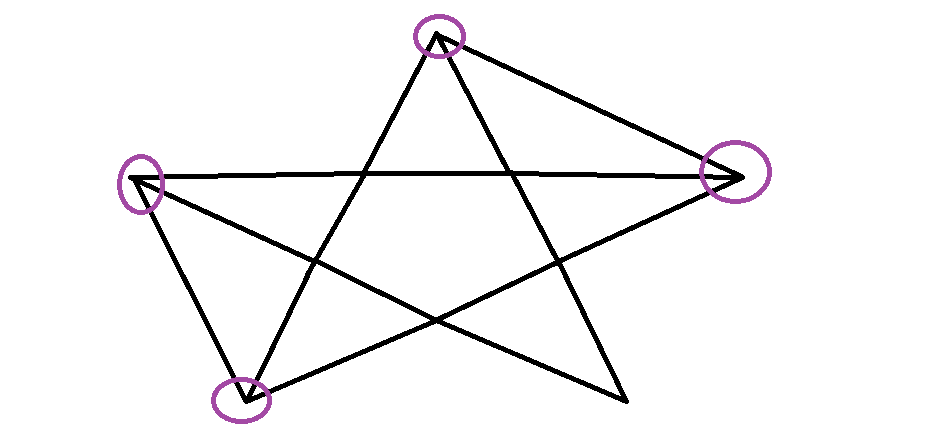
度數是奇數的點最多兩個
那如果所有點的度數都是偶數呢
會不會度數是奇數的點只有一個呢?
度數通通是偶數
-
隨便找到一個環
-
將這個環從圖上去掉
-
被影響到的點的度數都少二
-
剩下的圖的度數依然都是偶數
度數都是偶數
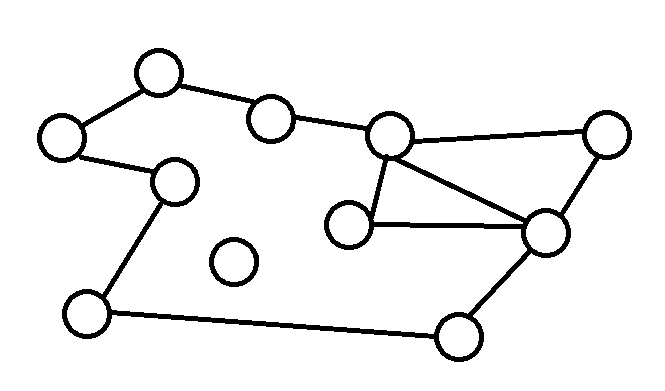
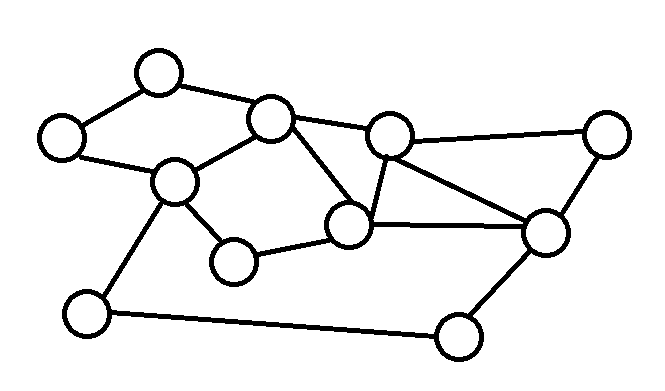
度數都是偶數


度數都是偶數
去掉一個環後,度數依然都是偶數
那就一直找到環,去掉
會不會有時候沒有環被拔掉呢?
會不會有時候沒有環被拔掉呢?
如果存在一條路徑,那端點的度數肯定是奇數
如果不存在路徑,那就沒有邊了
也就代表我們做完了
會不會有時候沒有環被拔掉呢?
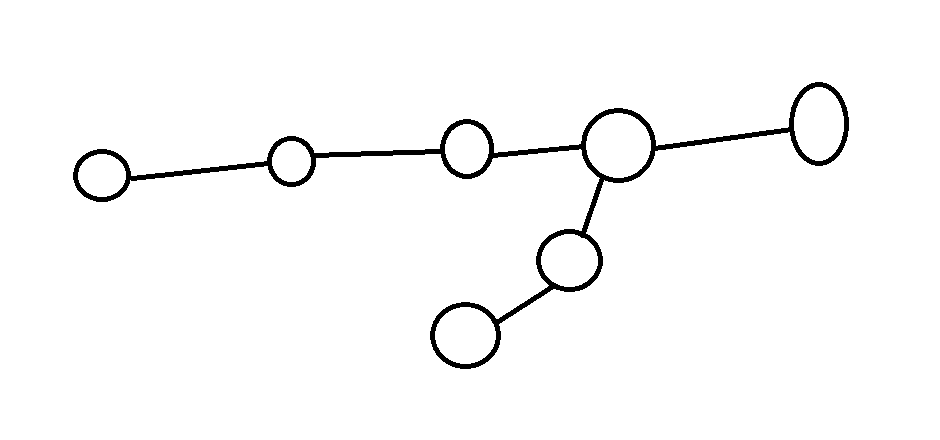
度數都是偶數的情況
一直拔掉環,直到結束
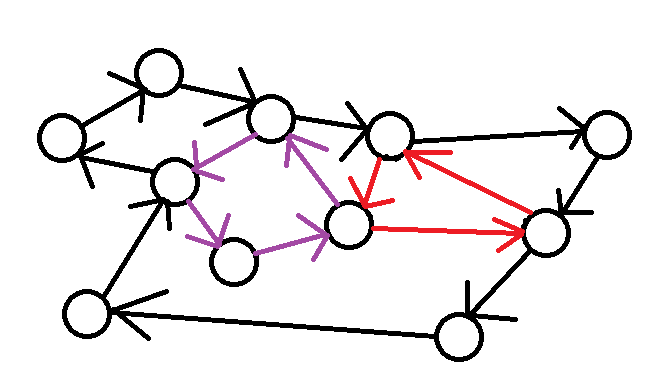
歐拉迴路
一筆畫問題中,起點和終點一樣

如果有兩個點度數是奇數呢?
把那兩個點連起來
那是不是變成了度數全都是偶數了?
歐拉路徑
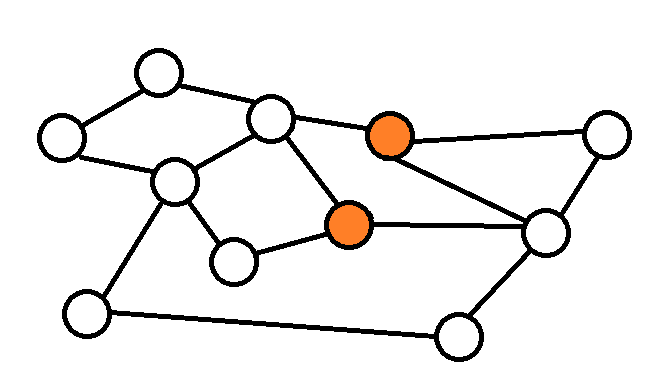
歐拉路徑
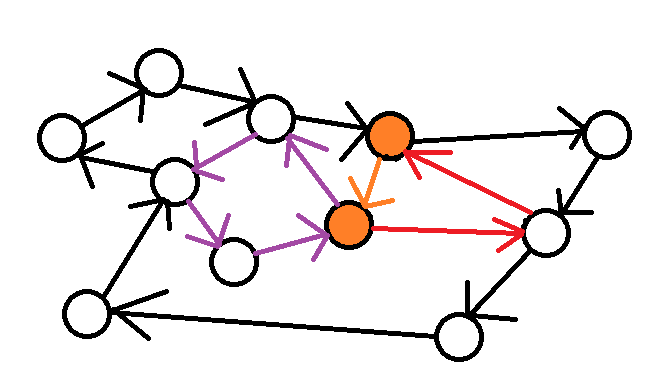
歐拉路徑
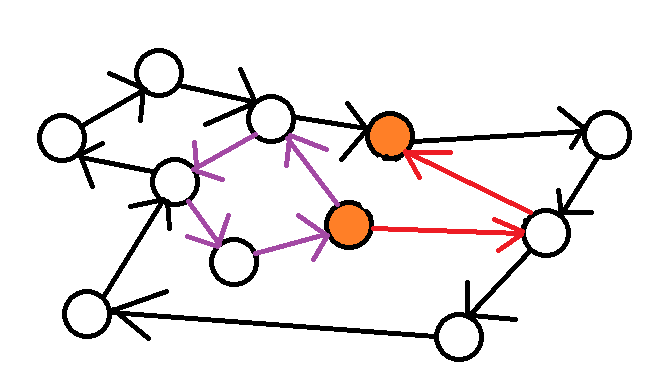
有沒有歐拉路徑/迴路
vector<int> v[N];
int cnt = 0;
// n 是點數
for (int i = 1; i <= n; ++i) {
cnt += (v[i].size() % 2);
}
if (cnt == 2) cout << "歐拉路徑";
else if (cnt == 0) cout << "歐拉迴路";
else cout << "NO";歐拉路徑
set<pair<int,int>> k;
vector<int> v[N];
void dfs(int x)
{
for(auto i:v[x]) if(k.find({i,x}) != k.end())
{
k.erase(k.find({i,x}));
k.erase(k.find({x,i}));
dfs(i);
}
ans.push_back(x);
}一筆畫問題
找到一個圖上經過點字典序最小的歐拉路徑
一筆畫問題
set<int> s[N];
set<pair<int,int>> k;
void dfs(int x) {
for(auto i:s[x]) if(k.find({i, x}) != k.end()) {
k.erase(k.find({i,x}));
k.erase(k.find({x,i}));
dfs(i);
}
ans.push_back(x);
}
樹直徑
在一棵樹上,最遠的兩點的距離是多少呢?


樹直徑
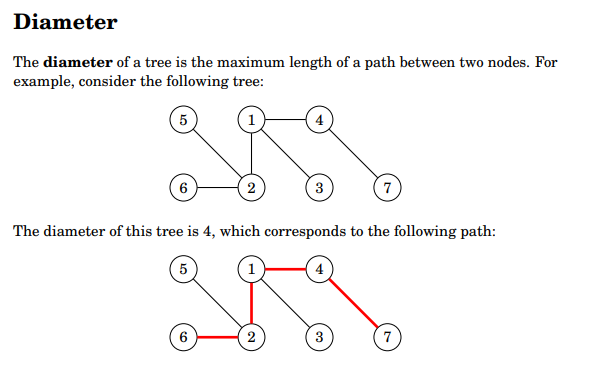
如何找離一個點最遠的點?
DFS
離A最遠的點是B
離B最遠的點是C
則B到C就是樹直徑
B到C是樹直徑?
如果有個D到B比C到B近?
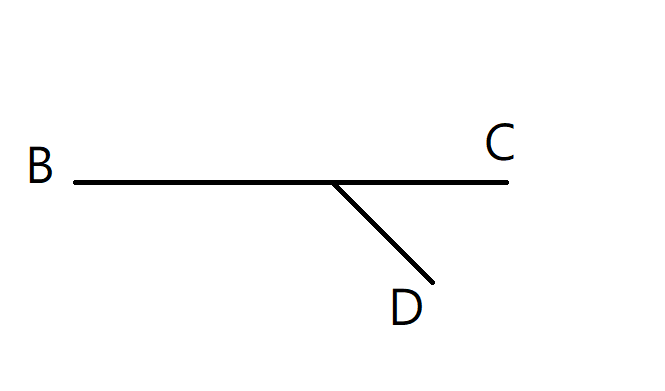
B到C是樹直徑?
離A最遠的B一定是樹直徑端點?
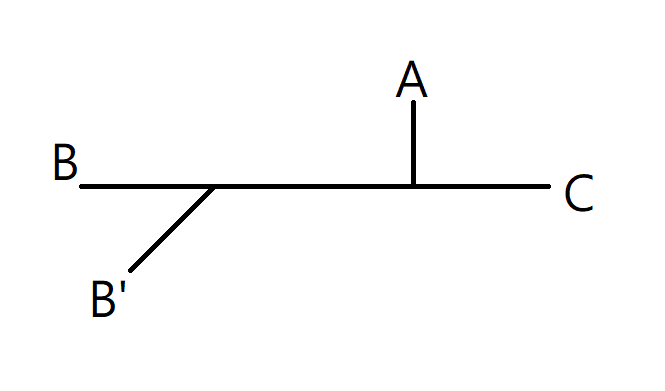
樹直徑
vector<int> g[N];
int ve, leng;
void dfs(int x, int p, int s) {
for(auto i : g[x]) {
if(i.first == p) continue;
dfs(i.first, x, s + i.second);
}
if( leng < s ) {
ve = x;
leng = s;
}
}
dfs(1, -1, 0);
leng = -1;
dfs(ve, -1, 0);
cout << leng << '\n';還有時間的話
例題練習
往右是其他有趣的小東西
地道問題
給定一張邊數和點數都少於10^6的有向圖
每條邊都有權重,且皆為非負整數
給定起點,求從起點走到其他所有點的最短路徑的長度和
還有請求出從其他所有點走回起點的最短路徑的長度和
地道問題
從起點做Dijkstra後加起來,再乘以二?
每條邊都是有向邊
所以去的時候的路徑和回來不會一樣
每條邊都是有向邊
所以去的時候的路徑和回來不會一樣
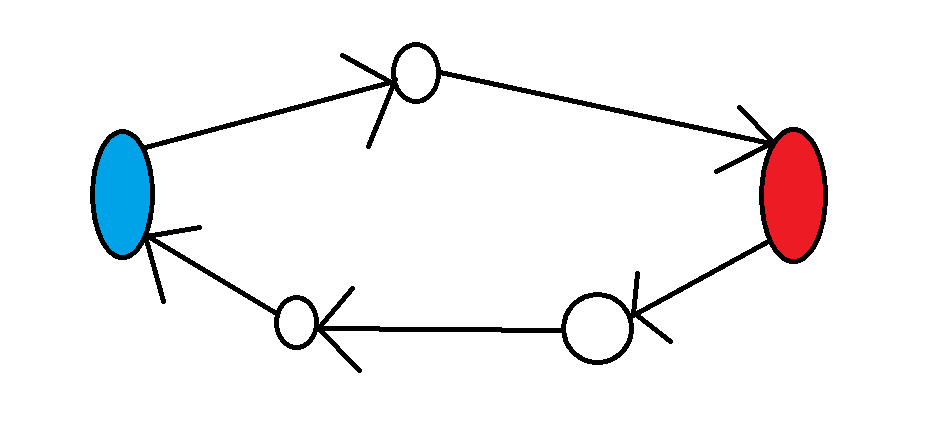
回來的路徑,可以想像成從起點走反路到點
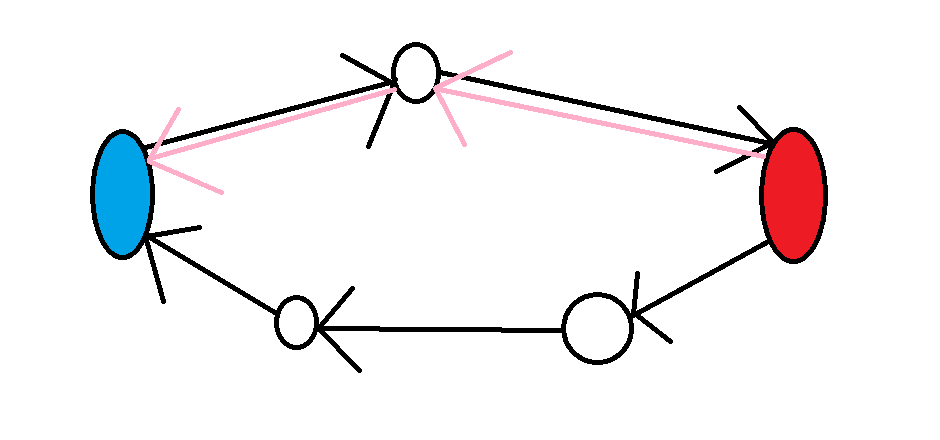
所有點回到起點
等價於將邊反轉後,從起點走到所有點
去:正常的做Dijkstra
回:將所以有邊反轉再做Dijkstra

圖論的最小圈測試
給一張無向圖,邊權都是一,點數最多500,
求長度最小的環的長度為多少?
圖論的最小圈測試
給一張無向圖,邊權都是一,點數最多500,
求長度最小的環的長度為多少?
圖論的最小圈測試
Floyd-Warshall

圖論的最小圈測試
for(int i = 0; i < m; i++) {
cin >> a >> b;
g[a][b] = 1;
}
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
g[i][j] = min(g[i][j],g[i][k]+g[k][j]);
int ans = INF;
for(int i = 1; i <= n; i++) ans = min(ans,g[i][i]);
if(ans == INF) cout << 0 << '\n';
else cout << ans << '\n';樹的三兄弟
給你一棵樹的前序與中序表示法
請輸出這棵樹的後序表示法
樹的三兄弟
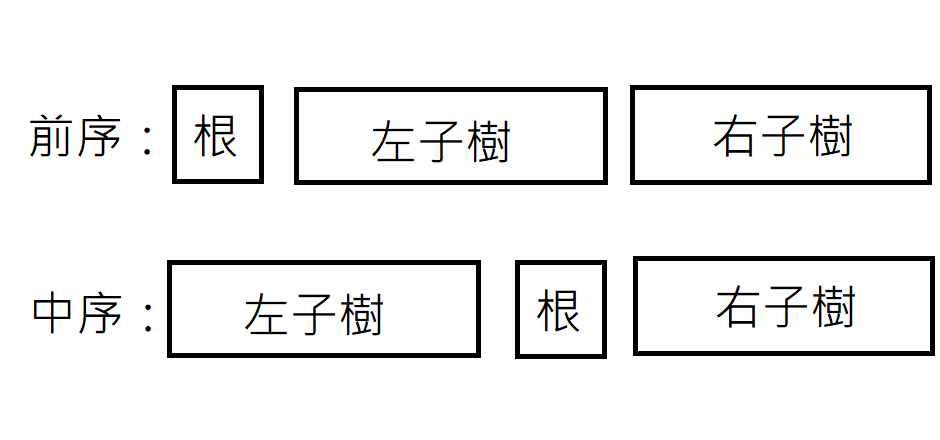
樹的三兄弟
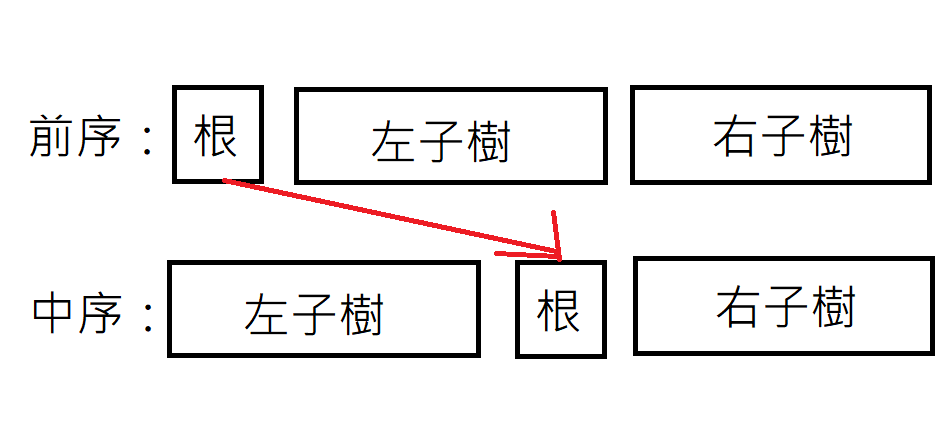
樹的三兄弟
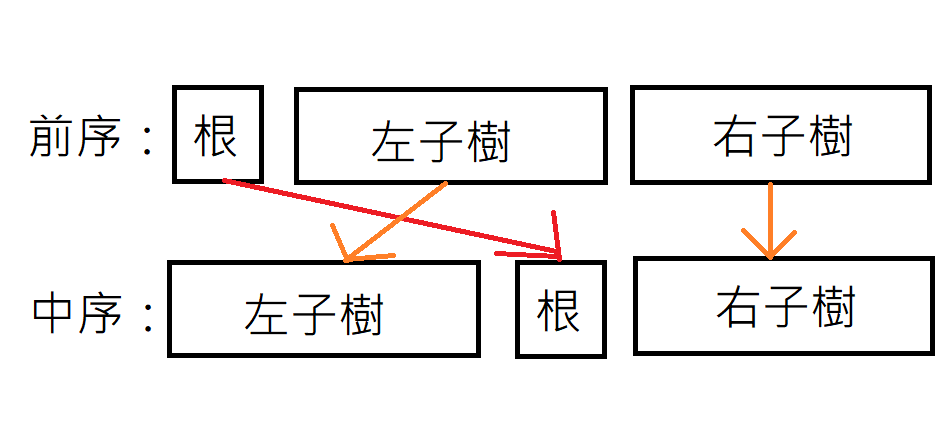
樹的三兄弟
void solve(string a, string b) {
int x = find(b.begin(), b.end(), a[0]) - b.begin();
int y = int(b.size())-x-1;
if(x > 0) solve(a.substr(1, x), b.substr(0, x));
if(y > 0) solve(a.substr(x + 1, y), b.substr(x + 1, y));
cout << a[0]; //根
}
signed main() {
string a, b;
while(cin >> a >> b) {
solve(a, b);
cout << '\n';
}
return 0;
}Floyd Cycle Detection
我把寶藏都藏在那了,自己去找吧
前提是你要會找環在哪
弗洛依德演算法
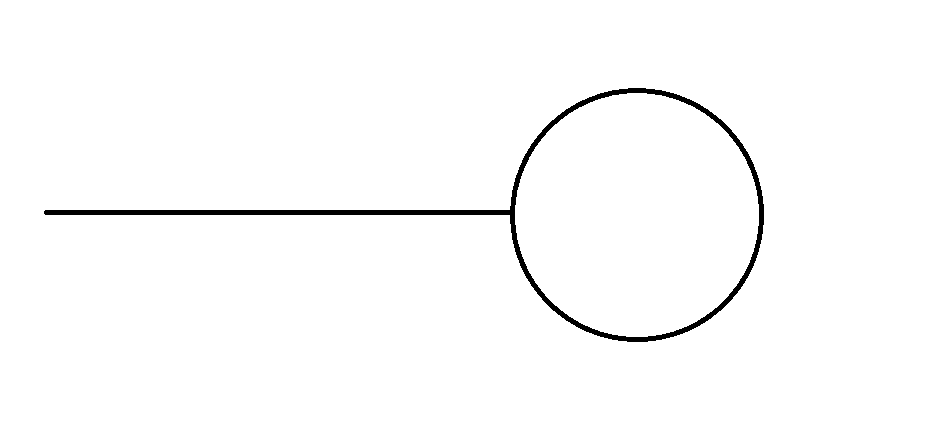
首先我們有一張長得像這樣的圖
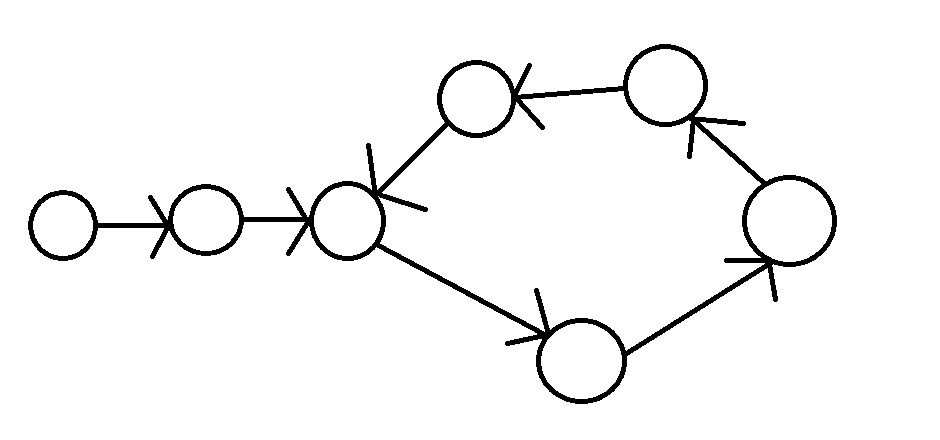
弗洛依德演算法
要如何找到環開始的地方呢?
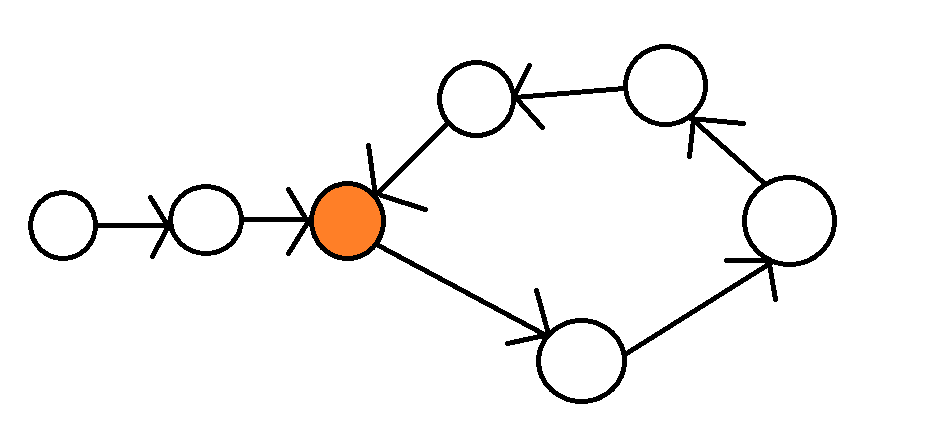
弗洛依德演算法
將一隻烏龜和一隻兔子放在起點
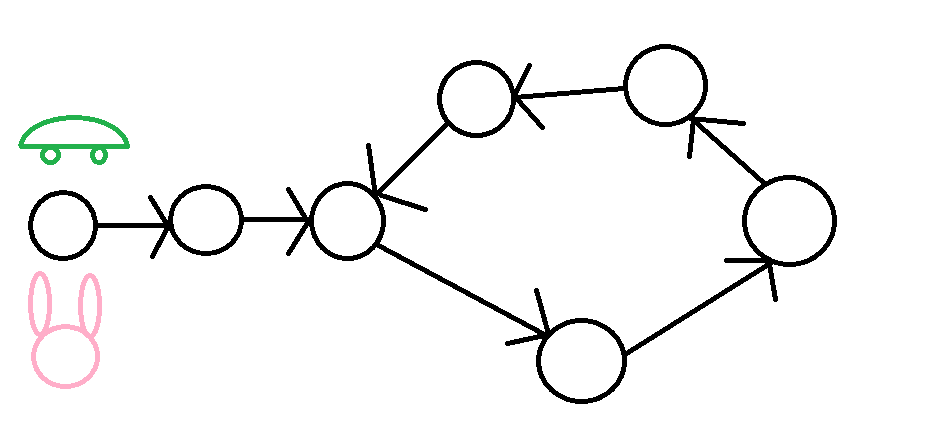
弗洛依德演算法
烏龜一次走一步
兔子一次走兩步
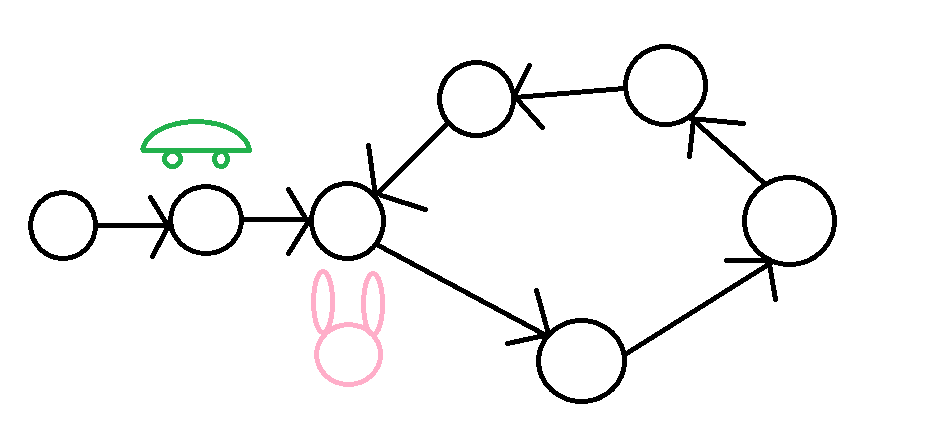
弗洛依德演算法
烏龜一次走一步
兔子一次走兩步
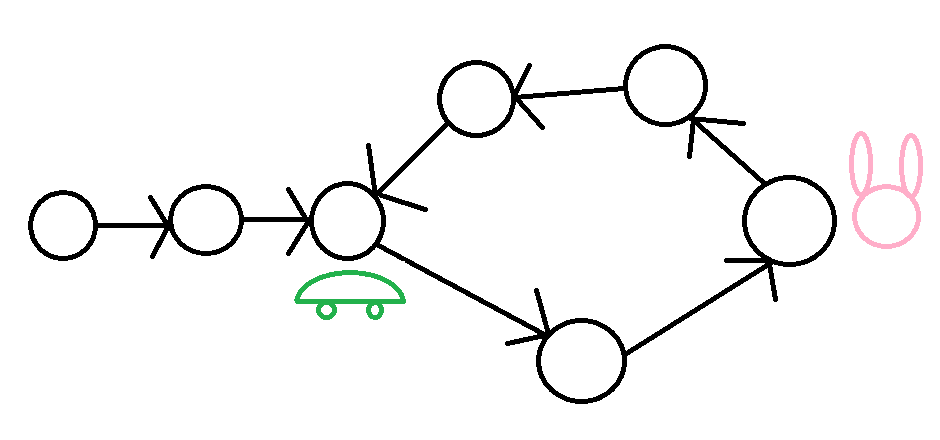
弗洛依德演算法
烏龜一次走一步
兔子一次走兩步
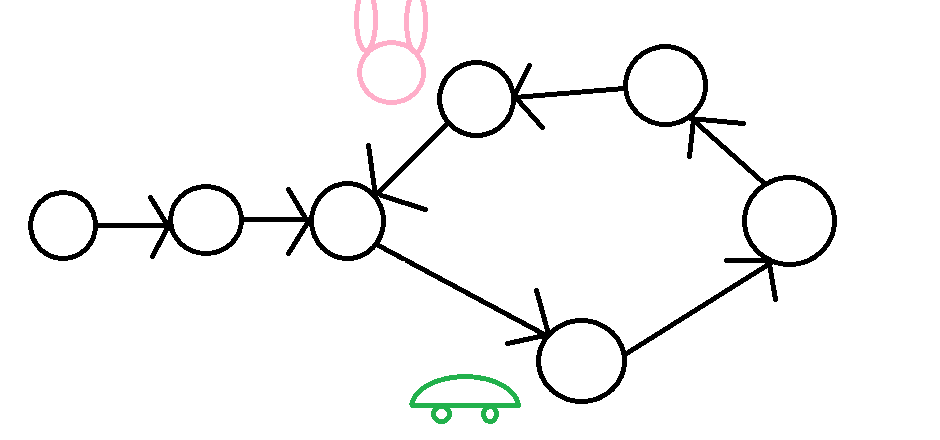
弗洛依德演算法
烏龜一次走一步
兔子一次走兩步
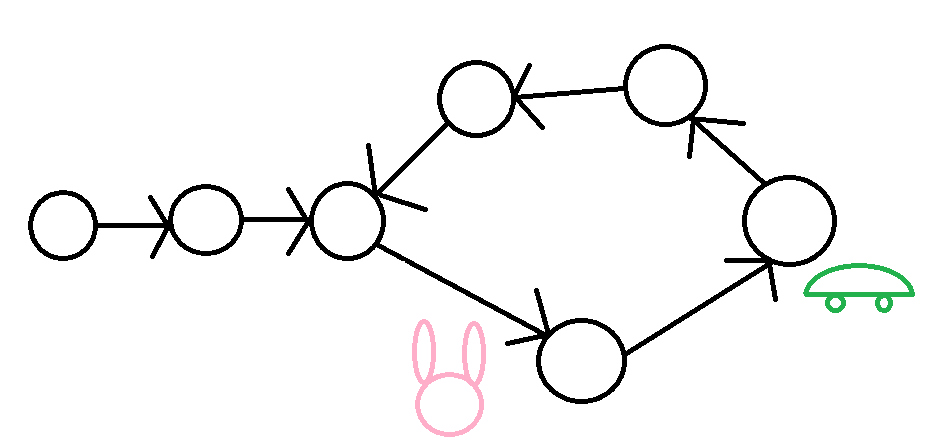
弗洛依德演算法
兔子和烏龜見面了
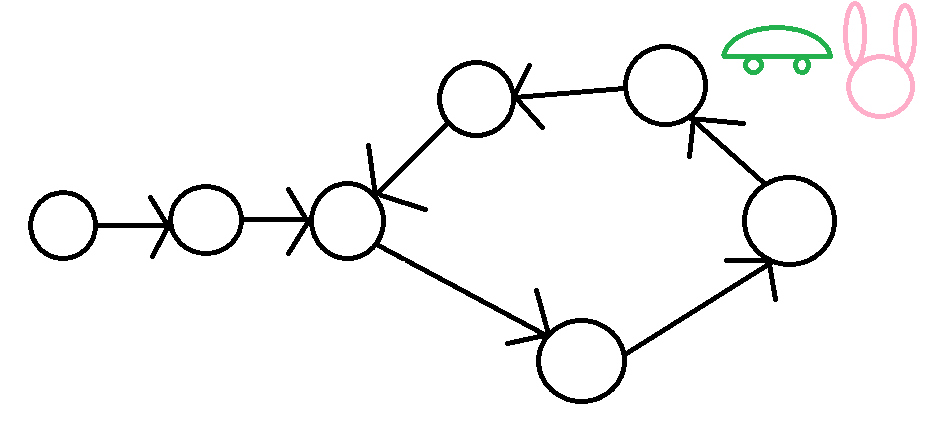
弗洛依德演算法
將兔子放回原點
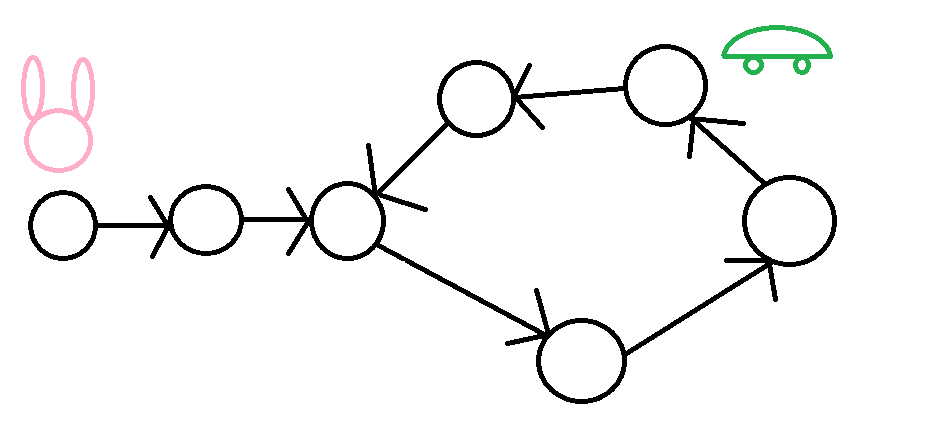
弗洛依德演算法
烏龜依舊一次走一步
兔子改成一次走一步
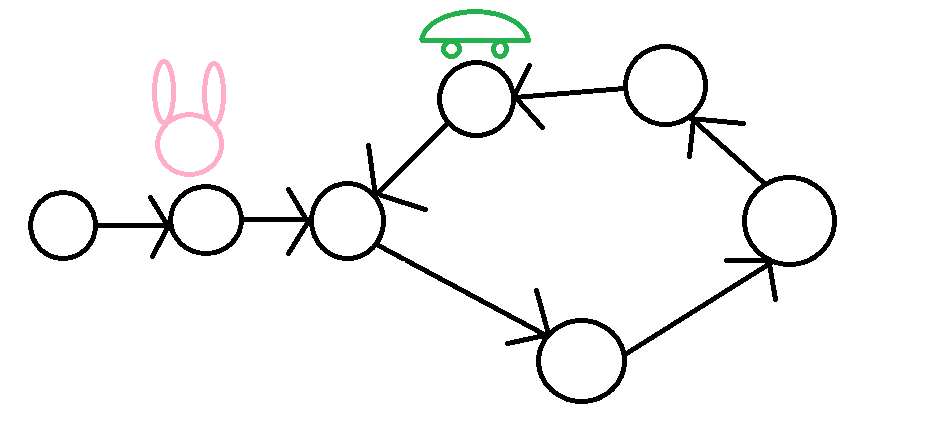
弗洛依德演算法
然後就在起點相遇了
神不神奇、厲不厲害><
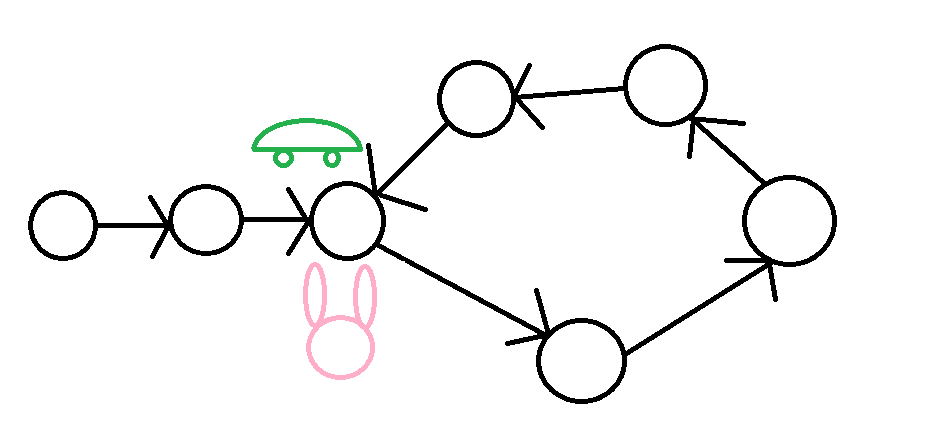
弗洛依德演算法WHY?
兔子和烏龜見面了
此時烏龜走的步數是環的倍數

弗洛依德演算法WHY?
此時烏龜走的步數是環的倍數加上柄的長度

弗洛伊德演算法
有向圖?
無向圖?
Knight's tour騎士之旅
我來自百萬歲月、千萬旅程的彼端
胸前的騎士徽章、尊貴的英姿、優雅的舉止,以及正直的心。
在在證明你是佛德賽的騎士。可是…
可是我從來沒見過劍柄上的家徽。請問你到底是從何而來?
騎士之旅
在一張西洋棋盤上,放上一位騎士。
請問這位騎士可以遵照西洋棋的規則,恰好走到每個格子一次嗎?
騎士之旅
Warnsdorf ’s rule
每次走到,能走的地方最少的格子
騎士之旅
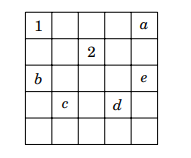
最短路徑
邊權只有 1 或 0
如果邊權都是 1
BFS
如果邊權都是 1
int dis[N];
queue<int> q;
q.push(1);
dis[1] = 0;
while (q.size()) {
int u = q.front();
q.pop();
for (auto i:v[u]) if (!visited[i]) {
visited[i] = 1;
dis[i] = dis[u] + 1;
q.push(i);
}
}BFS到底是怎麼運作的呢?
一層一層走下去
從離起點距離為 L 的點
走到離起點距離為 L + 1 的點
階層網路 Level Graph

邊權為 0 ?
這一條邊的兩端點應該在同個Level吧
BFS的順序
-
每次把距離為 L 的放進queue
-
接著從前面把距離為 L 的拿出來
-
把其相鄰的,也就是距離起點 L + 1 的點從後面放進 queue
和 L 相鄰的點中,邊權為零的邊連到的,應該也是距離為 L 的吧?
BFS的順序
邊權為 0 的邊連到的點要和距離為 L 的一起做
但是放在queue後面的是距離為 L + 1 的點
我能放在哪?
queue的前面,對吧?
邊權為 1 或 0
int dis[N];
deque<int> d;
d.push_back(1);
dis[1] = 0;
while (q.size()) {
int u = d.front();
d.pop_front();
for (auto i:v[u]) {
if (visited[i]) continue;
visited[i] = 1;
if (i.second == 1) {
d.push_back(i.first);
dis[i.first] = dis[u] + 1;
} else {
d.push_front(i.first);
dis[i.first] = dis[u];
}
}
}