Complexity

A problem may have multiple solutions

But how to decide which one is "better" ?

Some Valuation

Spend Less Time (Run Speed)
Use Less Space
Higher Correctness
Higher Compatibility
Low developing cost

Balance is important

When there is no computer, it takes 7.5 years to finish the census in US.
- When you finished... children have become adult...
If we just want to know the distribution of population, sampling is much useful.
After card reader (the earliest computer) came out, it takes only six weeks to finish census

But how to measure

Run it and measure is the most precise way.
But how to forecast?
Compatibility, developing cost highly depends on the implementation method and who implements it.
Accuracy has many perspectives.
- Implementing detail
- Number of cases
- Theory Analysis
How about time and spaces?

Some notes

The time each operation takes is not the same.

ex. division is much slower than addition.

ex. accessing different parts of memory takes different time.

Imput size

3x^2 < 10x \text{ if } x < 4

Generally, when the input size is small the deviation of time is small
We usually focus on those input size is huge.

The concept of time complexity

Summer homework

For most of us, doing addition is much faster than multiplication.

But...

The teacher offers two types of homework

10 multiplication problems / day
1st day 1 addition problem, 2nd day 2 addition problems, 3rd day 3 addition problems... and so on

Which one you will choose ?

addtion v.s. multiplication

Assume that it takes 5 secs for you to do an addition problem and 20 secs for a multiplication problem.

At the n-th day

Solution 1 takes

10 \times n \times 20 = 200n

Solution 2 takes

\frac{(n+1)\times n}{2}\times5=2.5(n^2+n)

At the n-th day

If n is small, ex n = 3 solution 2 is better

What if n is large ? ex. n = 365

200n\text{ v.s. }2.5(n^2+n)

We say that the growth(complexity) of operations needed of the solution is higher.

So for the large n, we should choose solution 1

Growth ?

Precisely, the growth of function

Briefly speaking, they grow in different level of speed

Concept of Infinity

For two function f(n) and g(n) when

which one is bigger ?

n \rightarrow \infty

Comparison

3n^2 + n + 20 \text{ v.s. } 100n \\ n^{100} \text{ v.s. } 2^n \\ n^2 \text{ v.s. } 10n\log{n} \\ 100^n \text{ v.s. } n! \\ 30\times2^n \text{ v.s. } 3^n\\ 100n \text{ v.s. } 200n

For n!

Concept of limit

3n^2 + n + 20 \text{ v.s. } 100n \\ n^{100} \text{ v.s. } 2^n \\ n^2 \text{ v.s. } 10n\log{n} \\ 100^n \text{ v.s. } n! \\ 30\times2^n \text{ v.s. } 3^n\\ 100n \text{ v.s. } 200n

if is close to 0 when n close to inf., we say that f(n) less than g(n)

if it is close to inf. then n close to inf., we say that f(n) is larger than g(n). (not presicely)

\frac{f(n)}{g(n)}

On a computer that performs 10^9 operation per sec.

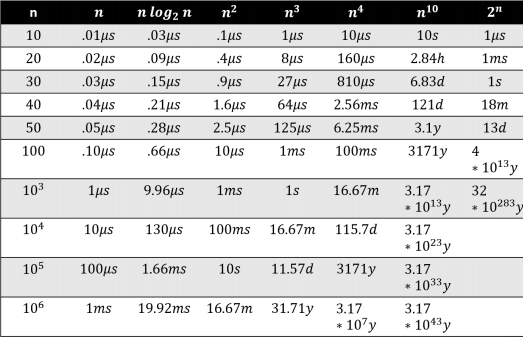
Concept of complexity

We assume all operations take the same time.

addition, subtraction, multiplication, division
modulation
bit operation
access memory
branch operation (if, else)
assign operation ( x= 5)

We calculate the numbers of operations and

check its complexity and measure runtime.

ex.

3n^2 + 2n + 7 \text{ , when } n =2000 \\ \text{ run time should be contant times of } 12004007

now computation power of a computer is generally

2\times 10^7 \text{ to } 8\times 10^7 \\\text{ operations per second}

asymptotic notation

The constant is not so important

Big-O notation

the upper bound of complexity

O(f(n))

Suppose the real time function is g(n)

then as

n \rightarrow \infty \text{ , } \frac{f(n)}{g(n)} \text{ is close to a constant or }\infty

example

Usually we take the "tight" upper bound.

3n^3+5n^2+10n+3 \in O(n^3) \\ f(n) \in O(n^2)\text{, then } f(n) \in O(n^3)\\ 1000 \in O(1)

Practice

3n^2 + n + 20 \text{ v.s. } 100n \\\\ n^{100} \text{ v.s. } 2^n \\\\ n^2 \text{ v.s. } 10n\log{n} \\\\ 100^n \text{ v.s. } n! \\\\ 30\times2^n \text{ v.s. } 3^n\\\\ 100n \text{ v.s. } 200n\\\\

O(n^2) \text{ v.s. } O(n)\\\\ O(n^{100}) \text{ v.s. } O(2^n)\\\\ O(n^2) \text{ v.s. } O(n\log{n})\\\\ O(100^n) \text{ v.s. } O(n!)\\\\ O(2^n) \text{ v.s. } O(3^n)\\\\ O(n) \text{ v.s. } O(n)\\\\

Little-o notation

the rigorous upper bound of f(n)

O(f(n))

Suppose the real time function is g(n)

then as

n \rightarrow \infty \text{ , } \frac{f(n)}{g(n)} \text{ is close to }\infty

Other asymptotic notations

Example

3n^3 + 5n^2 + 10n + 3 \notin o(n^3)\\ 3n^3 + 5n^2 + 10n + 3 \in o(n^4)\\ f(n) \in o(n^2) \text{, then } f(n) \in o(n^3)

Example

3n^3 + 5n^2 + 10n + 3 \notin o(n^3)\\ 3n^3 + 5n^2 + 10n + 3 \notin o(n^4)\\ f(n) \in o(n^2) \text{, then } f(n) \in o(n^3)

Big-omega notation

the lower bound of f(n)

\Omega(f(n))

Other asymptotic notations

3n^3 + 5n^2 + 10n + 3 \in \Omega(n^3)\\ f(n) \in \Omega(n^2) \text{, then } f(n) \in \Omega(n)

Little-omega notation

the strict lower bound of f(n)

\omega(f(n))

Other asymptotic notations

3n^3 + 5n^2 + 10n + 3 \in \Omega(n^2)\\ 3n^3 + 5n^2 + 10n + 3 \notin \Omega(n^3)\\

Big-theta notation

the strict upper bound and strict lower bound of f(n)

\Theta(f(n))

Other asymptotic notations

3n^3 + 5n^2 + 10n + 3 \in \Theta(n^3)\\ 3n^3 + 5n^2 + 10n + 3 \notin \Theta(n^4)\\ 3n^3 + 5n^2 + 10n + 3 \notin \Theta(n^2)\\

Usually use

Big-O and Big-theta

Worst Case

When analyzing complexity, we consider the worst case

Even the probability of it isn't large.

ex. Insertion Sort

from 1 ~ n, take the i-th element

move it to the correct position

ex. sorting [3, 2 ,1 ,4]

[3, 2 ,1, 4]
[2, 3 ,1, 4]
[2, 1, 3, 4]
[1, 2, 3, 4]
[1, 2, 3, 4]

Pseudo Code

for i from 1 to n
	for j from i-1 to 1
    	if( seq[j] < seq[i])
        	switch seq[j] and seq[i]
        else 
        	break

ex. sorting [3, 2 ,1 ,4]

[3, 2 ,1, 4]
[2, 3 ,1, 4]
[2, 1, 3, 4]
[1, 2, 3, 4]
[1, 2, 3, 4]

Best case

Already sorted

ex. [1, 2, 3, 4, 5]

O(n)

Worst case

Reverse Order

ex. [5, 4, 3, 2 ,1]

(n, n-1, n-2, ... 1)

\frac{n\times(n+1)}{2} \in O(n^2)

Think About it

"Asymptotic" complexity, why ?
What's the pros and cons of complexity analysis? It's always good to choose the lower time complexity?
Try to analyze your stack program.

O(f(n) + g(n)) = O(max(f(n), g(n))) \\\text{, why is this correct?}

\text{if } g1(n) \in O(f1(n))\text{, } g2(n) \in O(f2(n))\\ \text{then } g1(n)\times g2(n) \in O(f1(n)\times f2(n))\\ \text{why?}

In real word

If an algorithm has high space complexity and low time complexity.

Another one has low space complexity and high time complexity.

Which to choose?

when range large/small ? input size large/small?

Homework more practice with stack & queue

Min Stack

implement stack with queue

implement queue with stack

We will step in forest next week