Flood Fill
About Flood Fill
Imagine that you are pouring water into an icebox.
What is the movement of water ?
Maybe some blockes which have already
| B | B | B | B | B |
|---|---|---|---|---|
| B | O | O | O | |
| B | O | |||
| B | O | |||
| B |
| B | B | B | ||
| B | B | B | ||
| B | B | B | ||
How to implement ?
Naïve idea: Check every block and make them "flood" to the neighboring blocks.
suppose n*m ice box, it takes O(nm) per check
It takes a most O(n+m) rounds. (why?)
time complexity O(nm (n + m))
Spend to much time at "searching 'flooding' blocks"
Take a bit more
- Actually only the outer ring need to flood.
- Every block has only one chance to be in the outer ring
- We computer the "old" out most blocks, then generate the new out most blocks.
- use queue
Demo
| 1 | ||||
| 2 | ||||
| 3 | 1 | 5 | ||
| 4 | ||||
| 6 | ||||
|---|---|---|---|---|
| 7 | 2 | 8 | ||
| 9 | 3 | 1 | 5 | |
| 10 | 4 | |||
| 6 | ||||
|---|---|---|---|---|
| 7 | 2 | 8 | ||
| 9 | 3 | 1 | 5 | 13 |
| 10 | 4 | 12 | ||
| 11 |
Demo
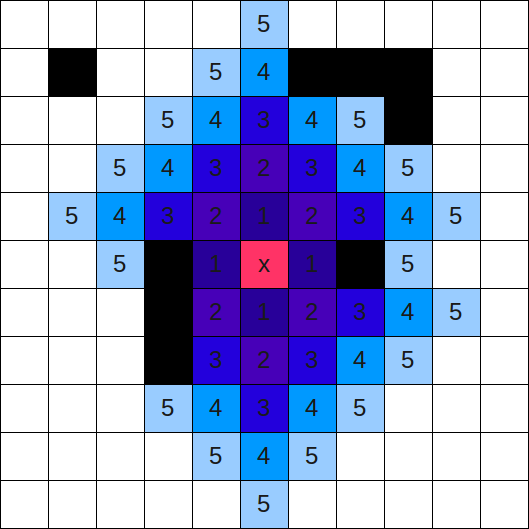
How to implement ?
- How to put a block into a queue?
- wrap (x,y) as a struct/class
- two queue for both x, y
- What about obstacles?
- treat it as already filled.
- How about multiple start points? (pouring water in several blocks at the beginning)
- Put all starting blocks into the queue
- How to handle edge blocks?
- use the imaginary outer ring. (n + 2) * (m + 2) icebox. and set the outer ring as obstacles.
- Simulating the "flooding" procedure, four(eight) directions need a lot of "if-else", how to?
- number of rounds are concerned with elements in the queue, and extending one blocks every time
- Every (possible flooded) block enters the queue exactly once.
- elements in queue is less than O(nm)
- For every element, extending is O(1)
- O(nm) * O(1) = O(nm)
Brain New Time complexity
- Naive way O(n^3)
- even O(n^4) is possible (n <= 100)
- If we used the previous queue method it becomes O(n^2)
- But how do we
- Spread simultaneously (queue spread one block per time)
- Calculate the num of color
- But how do we
Spread Simultaneously
Observe elements in the queue, the level of ring is non-decreasing.
ex. start at (2,2), (4,5), (10,3)
for convenience, assume spread in for direction
pre-elements in the queue
(2, 2), (4, 5), (10, 3),
(2, 3), (2,1), (1,2), (3,2), (4,6), (4,4), (3,5), (5,5), (10,4), (10,2), (9,3), (11,3)
(2,4), (1,3), (3,3), ……
So all we need to do is record the "level" of each block, and process the same "level" elements at the same round.
Recording Colors
- If we know how to spread simultaneously, we know how to maintain a number of colors at each round.
- Renew the number of colors while spreading
- Check our record each round.
- Don't forget to check what color is spreading now.
- Theoretically, every block will be spread 3 times.
- Asking the shortest path this time, what is connecting to the flood fill algorithm?
- Back to our conclusion
- The "level" of blocks is non-decreasing
- What is level representing? It's steps!
- The cost of one step is 1, so the "level" itself is actually the shortest path!
-
Why? And what if the cost of one step is not 1? Suppose each block has height, and the cost from one block to another is the difference of height.
-
- "Flood" from the outset, and stopped when encountering the first rat.
Recover
- At the previous flood file algorithm, the main data structure is a queue.
- What if we switch queue with the stack? What will happen?
| 1 | ||||
| 2 | ||||
| 4 | 1 | 5 | ||
| 3 | ||||
| 2 | 6 | |||
| 4 | 1 | 5 | 8 | |
| 3 | 7 | |||
| 2 | 6 | 9 | ||
| 4 | 1 | 5 | 8 | |
| 3 | 7 | 10 | ||
Imagine
If the map is large, we will see that water keeps going in some direction until it meets the end. And it comes back and goes in another direction.
- Like academic research
- Use queue is like, get the first knowing for every field, and go deeper for every field layer by layer.
- Use stack is like, get yourself master one field, then choose another field.
- Use queue is called Breadth-first search, BFS
- Use stack is called Depth-first search, DFS
- But actually, DFS won't use a stack in some cases.
| 1 | ||||
| 2 | ||||
| 4 | 1 | 5 | ||
| 3 | ||||
| 2 | 6 | |||
| 4 | 1 | 5 | 8 | |
| 3 | 7 | |||
| 2 | 6 | 9 | ||
| 4 | 1 | 5 | 8 | |
| 3 | 7 | 10 | ||
we don't have to store 2, 3, 4, 5 at the same time.
Push one, and we just process it at the next time.
Just use recursion
void dfs(int x, int y, int cur_dist){
dist[x][y] = cur_dist;
if(map[x+1][y] != '#' && dist[x+1][y] > cur_dist + 1)
dfs(x+1, y, cur_dist + 1);
if(map[x][y+1] != '#' && ....)
}(x, y) current coordinate
cur_dist = current steps
dist[x][y] is the shortest path length to (x,y)
call dfs(x_start, y_start, 0) call solve shortest path
(x_start, y_start) is where the cat is
Thinks
Can we use DFS for problem 1?
Or Can we use DFS for problem 2?
What are the pros and cons ? Time Complexity ?
A problem:
each block has a height, if height is less than a certain value, it flooded.
Asking how many flooded at the end?
Is BFS/DFS both applicable?
- Data structure
- queue v.s. stack
-
In the shortest path problem, the first answer is definitely correct
- yes v.s. no
-
space complexity
- In the worst case, the same, but generally DFS is smaller
- In some cases, DFS will have a difference in magnitude.
-
Implementing
- need queue v.s. use recursion to maintain a stack property
-
Others
- DFS in recursion needs to take stack overflow into consideration
BFS v.s. DFS
- At the first glance, BFS is much powerful than DFS
- In flood fill algorithm, DFS is nothing good with it; But in the future, DFS can be useful in a lots of cases.