Minimum Spanning Tree
by jacky860226
Undirected Weighted Graph
- A undirected graph whose edges have weights.
Definition
1
2
3
4
- Example:
- \(V=\{1,2,3,4\}\)
- \(E=\{\)
\((1,3), (1,2),\)
\((2,3), (4,2),\)
\((3,4)\)
\(\}\) - \(W\left(\left(1,2\right)\right)=13\)
2
8
13
7
6
$$G=(V,E)$$
- \(V\) is a set of vertices of \(G\) and \(E\) is a set of edges of \(G\).
- \(\forall e \in E\),
we define the weight function \(W(e)\) is the weight of \(e\).
Spanning Tree
- Give graph \(G=(V,E)\)
-
Spanning Tree is a connected tree \(T=(V,E')\) where
$$E' \subseteq E$$
2
4
3
2
1
8
13
7
6
Minimum Spanning Tree(MST)
- Give graph \(G=(V,E)\)
-
Minimum Spanning Tree is a Spanning Tree which
the sum of edge weights is minimum.
2
6
7
13
8
4
3
2
1
Greedy Algorithms to find MST
- Kruskal's algorithm
- Prim's algorithm
- Borůvka's algorithm
- ...
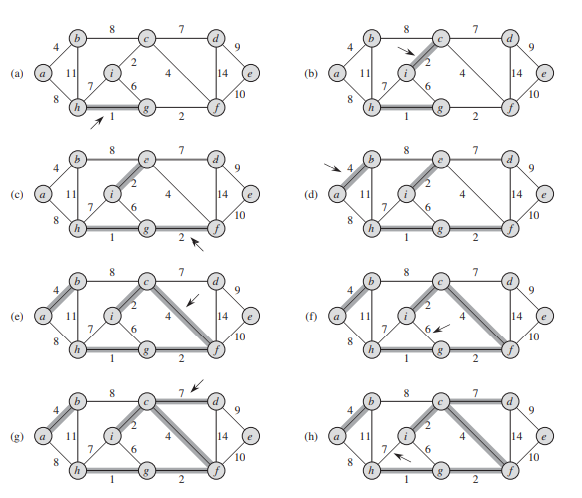
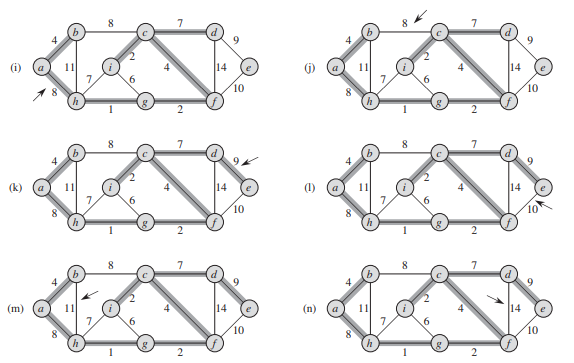
Kruskal's algorithm
- Input \(G=(V,E)\)
- Let \(E_s = E, E' = \{\}\)
- while ( \(E_s\) is not empty)
- Remove an edge \(e\) with minimum weight from \(E_s\)
- If add \(e\) into \(E'\) will not create a circle
- Add \(e\) into \(E'\)
- If \(T=(V,E')\) is a tree
- output \(T\) is a minimum spanning tree
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Kruskal's algorithm
6
7
13
8
2
4
3
2
1
Complexity
- Sort the edges by weight
- Using Union Find Set to maintain trees
O\left(E \log E + E \alpha\left(V\right)\right) = O(E \log E)
#include <tuple>
#include <vector>
#include <algorithm>
#include <numeric> // for iota(first, last, val) setting iterator value
using namespace std;
struct DSU // disjoint set no rank-comp-merge
{
vector<int> fa;
DSU(int n) : fa(n) { iota(fa.begin(), fa.end(), 0); } // auto fill fa from 0 to n-1
int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
void merge(int x, int y) { fa[find(x)] = find(y); }
};
int kruskal(int V, vector<tuple<int, int, int>> E) // save all edges into E, instead of saving graph via adjacency list
{
sort(E.begin(), E.end());
DSU dsu(V);
int mcnt = 0;
int ans = 0;
for (auto e : E)
{
int w, u, v; // w for weigth, u for start, v for destination
tie(w, u, v) = e;
if (dsu.find(u) == dsu.find(v))
continue;
dsu.merge(u, v);
ans += w;
if (++mcnt == V - 1)
break;
}
return ans;
}
CODE
How
to
Proof?
Edge inclusion lemma
$$G=(V,E)$$
- Let \(S\) be a subset of \(V\), and suppose \(e = (u, v)\) is the minimum cost edge of \(E\), with \(u\) in \(S\) and \(v\) in \(V-S\).
- Then \(e\) is in a certain minimum spanning tree of \(G\).
\(u\)
\(v\)
\(V-S\)
\(S\)
\(e\)
Proof
- Suppose \(T\) is a minimum spanning tree that does not contain \(e\).
\(v\)
\(u\)
\(S\)
\(V-S\)
\(u'\)
\(v'\)
a
b
c
d
e
\(e\)
\(e'\)
Proof
- Add \(e\) to \(T\), this creates a cycle.
- The cycle must have some edge \(e' = (u', v')\) with \(u'\) in \(S\) and \(v'\) in \(V-S\).
\(v\)
\(u\)
\(S\)
\(V-S\)
\(u'\)
\(v'\)
a
b
c
d
e
\(e\)
\(e'\)
Proof
- By definition, we have \(W(e) \le W(e')\)
- \(W(e) = W(e')\) because \(T\) is a minimum spanning tree.
\(v\)
\(u\)
\(S\)
\(V-S\)
\(u'\)
\(v'\)
a
b
c
d
e
\(e\)
\(e'\)
Proof
- By definition, we have \(W(e) \le W(e')\)
- \(W(e) = W(e')\) because \(T\) is a minimum spanning tree.
- We can remove \(e'\) and add \(e\) to create a new tree \(T'\)
- \(T'\) must be a minimum spanning tree!
\(v\)
\(u\)
\(S\)
\(V-S\)
\(u'\)
\(v'\)
a
b
c
d
e
\(e\)
\(e'\)
Prim's algorithm
- \(G=(V,E)\)
- Let \(S=\{v_0\}\) where \(v_0 \in V\)
- Let \(E'=\{\}\)
- while(\(V-S\) not empty)
- Let \(e = (u, v)\) is the minimum cost edge of \(E\), with \(u\) in \(S\) and \(v\) in \(V-S\)
- Add \(e\) into \(E'\)
- add \(v\) into \(S\)
-
If \(T=(V,E')\) is a tree
- output \(T\) is a minimum spanning tree
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d,f\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d,f,b\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d,f,b,e\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d,f,b,e,c\}\)
Prim's algorithm
a
d
b
g
f
c
e
5
7
9
15
6
8
11
9
7
8
5
\(S = \{a,d,f,b,e,c,g\}\)
Complexity
- Using Binary heap maintain edges
- Using adjacency list
O\left(E\log V\right)
Complexity
- Using Fibonacci heap maintain edges
- Using adjacency list
O\left(E + V\log V\right)
#include <vector>
#include <queue>
#include <utility>
using namespace std;
#define enp pair<int, int> // pair<edge_val, node>
int prim_pq(vector<vector<enp>> E){
vector<bool> vis;
vis.resize(E.size(), false);
vis[0] = true;
priority_queue<enp, vector<enp>, greater<enp>> pq;
for(auto e: E[0]){
pq.emplace(e.first, e.second);
}
int ans = 0; // min value for MST
while(pq.size()){
int w, v; // edge-weight, vertex index
tie(w, v) = pq.top();
pq.pop();
if(vis[v])
continue;
vis[v] = true;
ans += w;
for(auto e: E[v]){
if(!vis[e.second])
pq.emplace(e.first, e.second);
}
}
return ans;
}
CODE
UVa 908
Tioj 1211
Minimum Bottleneck Path
-
\(G=(V,E)\)
-
For any path \(p\), we call a \(Bottleneck(p)\) is an edge \(e \in p\)
which \(W(e)\) is maximum -
A Minimum Bottleneck Path from \(u\) to \(v\)
is a path \(p\) from \(u\) to \(v\) which \(W(Bottleneck(p))\) is minimum
Minimum Bottleneck Path
4
8
7
9
11
8
6
15
9
7
5
e
c
f
g
b
d
a
Minimum Bottleneck Path
4
8
7
9
11
8
6
15
9
7
5
e
c
f
g
b
d
a
Minimum Bottleneck Lemma
- \(G=(V,E)\)
- Let \(T=(V,E')\) is a Minimum Spanning Tree of \(G\)
- \(\forall u,v \in V\):
- \(path(u,v)\) in \(T\) is a Minimum Bottleneck Path in \(G\)