Continuous Control with Deep RL

Timothy P. Lillicrap, Jonathan J. Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver & Daan Wierstra Google Deepmind London, UK

Presented by: Tyler Becker

\mathcal{A} = \mathbb{R}

Motivation

\mathcal{A} = \mathbb{R}

s_i

Q(s_i, a_1)

Q(s_i, a_2)

Q(s_i, a_3)

\mathcal{A} = \mathbb{R}^6

Even extremely coarse discretization: rotate CCW, rotate CW, no rotation $$|\mathcal{A}| = 3^6 = 729$$

Problem: Large Action Space

\mathcal{A} = \mathbb{R}^6

Even extremely coarse discretization: rotate CCW, rotate CW, no rotation $$|\mathcal{A}| = 3^6 = 729$$

Problem: Large Action Space

|\mathcal{A}|\text{?}

Mnih, V., Kavukcuoglu, K., Silver, D. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015). https://doi.org/10.1038/nature14236

Problem: Complex State Value Function

Motivation

Want continuous $\mathcal{A}$ compatibility as well as the general applicability provided by the Universal Approximation Theorem

"standard multilayer feedforward networks are capable of approximating any measurable function to any desired degree of accuracy, in a very specific and satisfying sense"

Hornik, Kurt, et al. “Multilayer Feedforward Networks Are Universal Approximators.” Neural Networks, vol. 2, no. 5, Jan. 1989, pp. 359–66. DOI.org (Crossref), https://doi.org/10.1016/0893-6080(89)90020-8.

Contributions

Deep Q-Learning

Deterministic Policy Gradients

Deep Deterministic Policy Gradients

- Separate target networks

- Batch learning

- NN function approximation

- continuous $\mathcal{A}$

- Actor-critic sample efficiency

Background

DPG

DQN

DPG

Deterministic Policy Gradient

Previously for RL, we had:

$\pi : \mathcal{S} \rightarrow \mathbb{R}^{|\mathcal{A}|}$

$$\pi_\theta(a|s;\theta) = \mathbb{P}[a|s;\theta]$$

What if $\mathcal{A} = \mathbb{R}^N $?

Instead, have the policy be deterministic

$\pi : \mathcal{S} \rightarrow \mathcal{A}$

$$\pi_\theta(s|\theta) = a$$

DPG

$\pi : \mathcal{S} \rightarrow \mathcal{A}$

$$\pi_\theta(s|\theta) = a$$

How do we optimize $\theta$ for $\pi_\theta$?

Want $\pi_\theta(s) = \argmax_a\left\{Q(s,a)\right\}$

New unknown variable that comes back despite getting rid of it with determinization:

$$\pi_\theta(a|s;\theta) = \mathbb{P}[a|s;\theta] \rightarrow \pi_\theta(s|\theta) = a$$

DPG

How do we optimize $\theta$ for $\pi_\theta$?

Want $\pi_\theta(s) = \argmax_a\left\{Q(s,a)\right\}$

Actor $\pi_\theta(s)$

Critic $Q_\phi(s,a)$

Climb Q gradient

Descend TD MSE gradient

\ell(\boldsymbol{\phi})=\frac{1}{2} \underset{s, a, r, s^{\prime}}{\mathbb{E}}\left[\left(r+\gamma Q_{\phi}\left(s^{\prime}, \pi_{\theta}\left(s^{\prime}\right)\right)-Q_{\phi}(s, a)\right)^{2}\right]

U(\theta) = \mathbb{E}[Q_\phi(s,\pi_\theta(s))]

DQN

Deep Q-Network

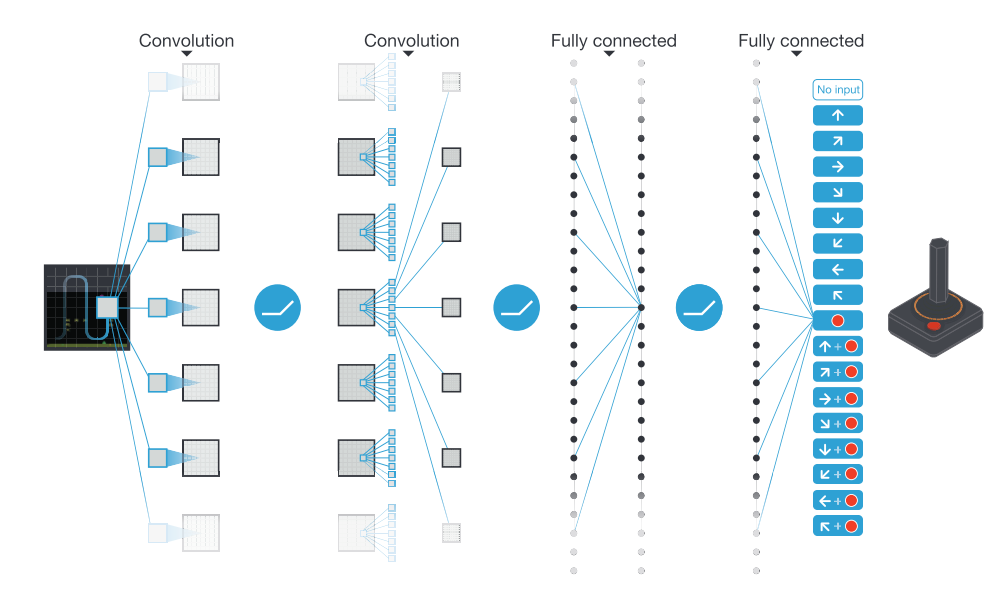
DQN

Vanilla Q-learning

% \theta \leftarrow \theta + \alpha\nabla_\theta Q_\theta(s,a)(r + \gamma\max_{a'}Q(s',a') - Q(s,a)) L(\theta) = \left( r + \gamma\max_{a'}Q(s',a') - Q(s,a)\right)^2

Samples $(s,a,r,s')$ highly correlated

Batches consist of 1 sample

Moving Targets

Changing $\theta$ to move $Q_\theta(s,a)$ towards target

($r + \gamma\max_{a'}Q_\theta(s',a')$) also changes target in the process

Maintain an experience buffer to sample from randomly

Maintain a separate target network $Q_\phi(s',a')$ that is frozen intermittently to prevent target values from varying wildly with current $Q$ estimates

Problems

Solutions

Problem Setting

Have DQN which works well for discrete actions spaces and can approximate complex Q functions

Have DPG which works with continuous $\mathcal{A}$, but complexity of Q function that we are able to approximate is dependent on the complexity of the parametric model that we choose

Problem Setting

In combining DQN and DPG, we are now given more freedom in the state/action space complexity of the problems we wish to solve

Given direct state information:

DNN taking body position/velocity

Given direct pixel data to be processed by CNN

Context In Literature

DQN
- Mnih, V., Kavukcuoglu, K., Silver, D. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015). https://doi.org/10.1038/nature14236
DPG
- Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., & Riedmiller, M. (2014). Deterministic Policy Gradient Algorithms. In Proceedings of the 31st International Conference on Machine Learning (pp. 387–395). PMLR.
TRPO - Solves continuous action space RL without actor-critic architecture
- Lower sample efficiency than DDPG but more stable
- John Schulman, Sergey Levine, Philipp Moritz, Michael I. Jordan, & Pieter Abbeel. (2015). Trust Region Policy Optimization.

Approach

Deterministic Actor Network: $\mu(s|\theta^\mu)$
Critic Network: $Q(s,a|\theta^Q)$
Target Networks: $\mu(s|\theta^{\mu'}),Q(s,a|\theta^{Q'})$

Exploration:

Softmax sample from $a\in\mathcal{A}$ via $Q(s,a)$

\mu'(s_t) = \mu(s_t|\theta_t^\mu) + \mathcal{N}_t

No explicitly listed $a\in \mathcal{A}$ to choose from

Approach

L_c = \frac{1}{N}\sum_i(r_i + \gamma Q'(s_{i+1}\mu'(s_{i+1}|\theta^{\mu'})|\theta^{Q'}) - Q(s_i,a_i|\theta^{Q}))^2

For critic: want to minimize TD MSE

For actor: want to climb Q gradient

\nabla_{\theta^\mu}Q(s,a|\theta^Q) = \nabla_{a}Q(s,a|\theta^Q)\nabla_{\theta^\mu}\mu(s|\theta^\mu)

For target networks: want steady/stable convergence

\begin{aligned} \theta^{Q^{\prime}} & \leftarrow \tau \theta^{Q}+(1-\tau) \theta^{Q^{\prime}} \\ \theta^{\mu^{\prime}} & \leftarrow \tau \theta^{\mu}+(1-\tau) \theta^{\mu^{\prime}} \end{aligned}

(\tau \ll 1)

Approach

Experiments

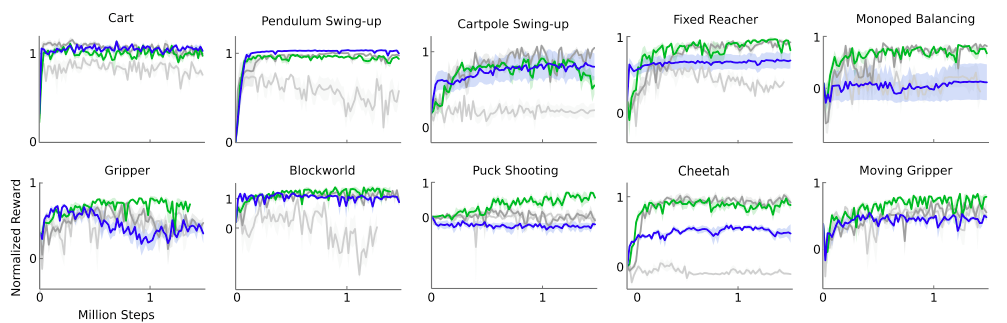
Batch Normalization

Target Network

Target Network + Batch Normalization

Pixel-only inputs

Batch Normalization

NN's sensitive to input distributions
- Input distribution of $\mathcal{N}(1,1)$ much more likely to train more effectively than input distribution of $\mathcal{N}(10^6,10)$
Input distributions change with environment and training progress
Solution: transform minibatch for each layer to $\mathcal{N}(1,1)$
- Maintain running avg of $\mu, \sigma$ for testing
- Consistent inputs across problems & training progress

https://www.jeremyjordan.me/batch-normalization/

Experiments

Batch Normalization

Target Network

Target Network + Batch Normalization

Pixel-only inputs

Experiments

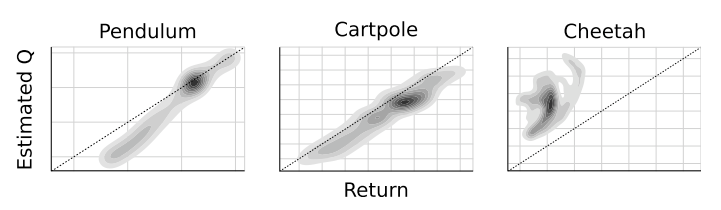
Computational Resources

Substantially fewer experience steps required for DDPG relative to DQN (~20x)
Low-dimensional networks with ~130,000 parameters
High-dimensional networks with ~430,000 parameters

Limitations

Does not work in partially observable environments

Yan Duan, Xi Chen, Rein Houthooft, John Schulman, & Pieter Abbeel. (2016). Benchmarking Deep Reinforcement Learning for Continuous Control.

Original paper does not compare to other algorithms

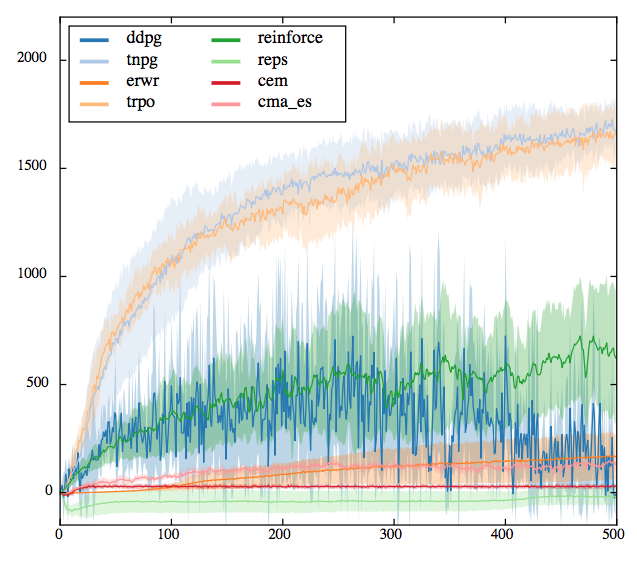
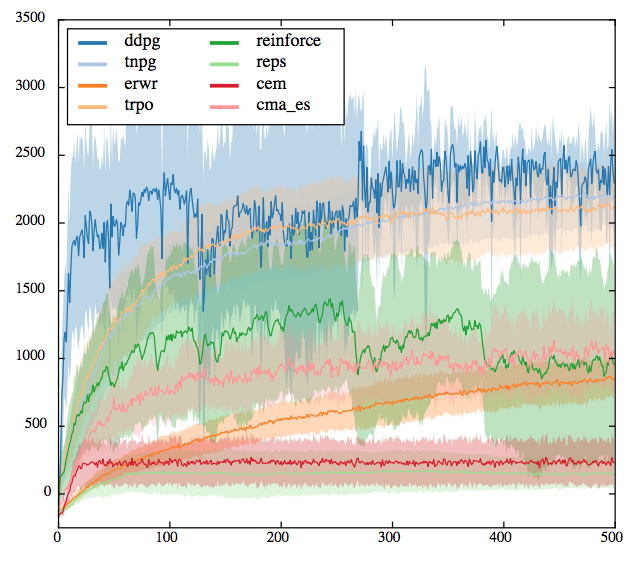
Walker

Half-Cheetah

Impact & Legacy

Inclusion in plenty of RL overviews

Effort to quantify sample efficiency

- Measuring Progress in Deep Reinforcement Learning Sample Efficiency - Dorner

Future Work

Applying Rainbow DQN concepts
Asynchronous policy updates with multiple agents
- Deep Reinforcement Learning for Robotic Manipulation with Asynchronous Off-Policy Updates - Gu et al.

Contributions (Recap)

Deep Q-Learning

Deterministic Policy Gradients

Deep Deterministic Policy Gradients

- Separate target networks

- Batch learning

- NN function approximation

- continuous $\mathcal{A}$

- Actor-critic sample efficiency