DESPOT-\(\alpha\)

DESPOT-α: Online POMDP Planning With Large State And Observation Spaces

Neha P Garg, David Hsu and Wee Sun Lee

Presented by Tyler Becker

Motivation

Small \(|\mathcal{O}|\)

Large \(|\mathcal{O}|\)

Contributions

  • Extension of DESPOT to large observation spaces
  • Minimizing overhead of expansion to large observation spaces
    • Parallelizable leaf node evaluation with \(\alpha\)-vectors
  • Extension of Hyp-DESPOT to fully parallelized HyP-DESPOT-\(\alpha\)

DESPOT + Weighted PF + \(\alpha\) vectors

Background

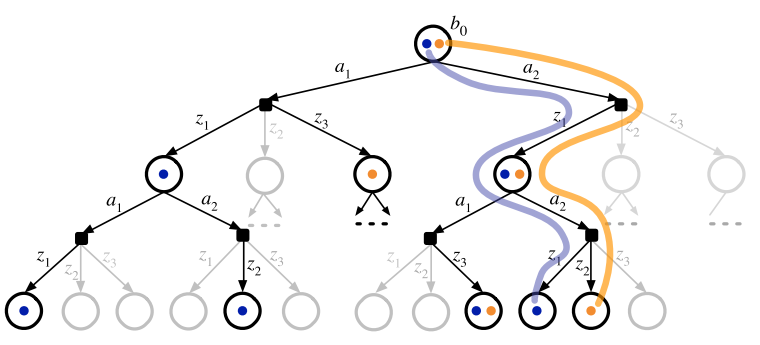
DESPOT

Determinized Scenarios:

s',z' = G(s,a,\phi)

Overarching "anytime" algorithmic goal: 

\text{minimize } \epsilon(b_0) = \mu(b_0) - l(b_0)
\mu(b)=\max \left\{\ell_{0}(b), \max _{a \in A}\left\{\rho(b, a)+\sum_{z \in Z_{b, a}} \mu\left(b^{\prime}\right)\right\}\right\} \\ \ell(b)=\max \left\{\ell_{0}(b), \max _{a \in A}\left\{\rho(b, a)+\sum_{z \in Z_{b, a}} \ell\left(b^{\prime}\right)\right\}\right\} \\ U(b)=\max _{a \in A}\left\{\frac{1}{\left|\boldsymbol{\Phi}_{b}\right|} \sum_{\boldsymbol{\phi} \in \boldsymbol{\Phi}_{b}} R\left(s_{\boldsymbol{\phi}}, a\right)+\gamma \sum_{z \in Z_{b, a}} \frac{\left|\boldsymbol{\Phi}_{b^{\prime}}\right|}{\left|\boldsymbol{\Phi}_{b}\right|} U\left(b^{\prime}\right)\right\}
b
a
o
b'
b',r \leftarrow G_{PF}(b,a)
s_i',r_i \leftarrow G(s_i,a)
w_i '= \eta w_i\mathcal{Z}(o|s_i,a,s_i')
r(b,a) = \sum_iw_ir_i
\eta = \left(\sum_i w_i\mathcal{Z}(o|s_i,a,s_i') \right)^{-1}

Propagate

Reweight

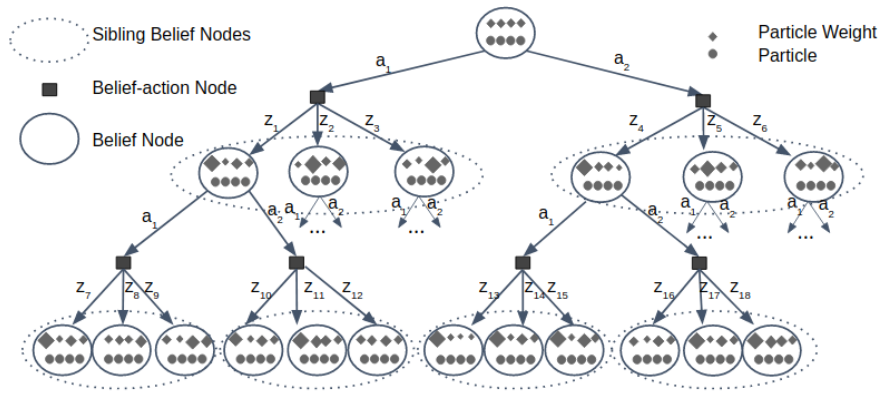
Weighted PF

\(\alpha\) vectors

V^\pi(b) = \sum_s b(s)V^\pi(s) = \alpha_\pi^Tb
V^*(b) = \max_\pi\alpha_\pi^Tb
V(s) = \max_a\{R(s,a) + \gamma\mathbb{E}[V(s')]\}
\mathbb{E}[V(s')] = \sum_{s'}T(s'|s,a)V(s')

MDP Bellman

POMDP Bellman

V(b) = \max_a\{R(b,a) + \gamma\mathbb{E}[V(b')]\}
R(b,a) = \sum_sb(s)R(s,a)
\mathbb{E}[V(b')] = \sum_{z\in \mathcal{Z}}p(z|b,a)V(\tau(baz))
p(z|b,a) = \sum_{s'}p(z|s',a)\sum_s p(s'|s,a)b(s)
p(z|b,a) = \sum_{s'}p(z|s',a)\sum_s p(s'|s,a)b(s)

DESPOT utilizes determinized scenarios

s' = G(s,a), \quad s' = G(s'_-,a,\phi), \quad s_+ = G(s,a,\phi)
P(s'|s,a) = \begin{cases} 1 \quad & s' = s_+ \\ 0 \quad & \text{otherwise} \end{cases}
p(z|b,a) \leftarrow \sum_{s'}p(z|s',a)b(s'_-)
\begin{aligned} V_{n+1}(b) &= \max_a\left\{\sum_{s}w_b(s)R(s,a) + \gamma\sum_{z}\sum_{s'}w_b(s'_-)p(z|s',a)\alpha_{n,\tau(baz)}(s')\right\} & (1)\\ &= \max_a\left\{\sum_{s}w_b(s)R(s,a) + \gamma\sum_{z}\sum_{s}w_b(s)p(z|s_+,a)\alpha_{n,\tau(baz)}(s_+)\right\} & (2)\\ &= \max_a\left\{\sum_{s}w_b(s)\left(R(s,a) + \gamma\sum_{z}p(z|s_+,a)\alpha_{n,\tau(baz)}(s_+)\right)\right\} & (3)\\ &= \sum_{s}w_b(s)\max_a\left\{\left(R(s,a) + \gamma\sum_{z}p(z|s_+,a)\alpha_{n,\tau(baz)}(s_+)\right)\right\} & (4)\\ &= \sum_{s}w_b(s)\alpha_{n+1,b}^{a^*}(s) & (5) \\ &= w_b^T\alpha_{n+1,b}^{a^*} & (6) \end{aligned}

Assuming \(\alpha\)'s are similar among sibling nodes, we can estimate value of sibling nodes without having to recalculate \(\alpha\)

Approach

a^* = \text{argmax}_{a\in \mathcal{A}}\bar{Q}(b,a)
a_1
a_2
a_3
Q(b,a_1)
Q(b,a_2)
Q(b,a_3)
b

Exploration

z^* = \text{argmax}_{z \in C_{b,a^*}}\left\{\text{WEU}(\tau(b,a^*,z))\right\}
a^*
b
z_1
z_2
z_3
\text{WEU}(\tau(b,a^*,z)) = p(z|b,a^*)(\epsilon(b') - \xi\epsilon(b_0))

Exploration

\epsilon(b) = \bar{V}(b) - \underline{V}(b)

\(\xi\) : hyperparameter controlling desired leaf node uncertainty

Leaf Node Expansion

a_1
a_2
a_3

Expand all \(a \in \mathcal{A}\) 

z
z
z
z
z
z
z
z
z
z
z
z

propagate particles / collect observations

rollout for lower bound \(\alpha(s)\)

Leaf Node Expansion

a_1
z_1
z_2
z_3

Create \(C \le K\) new beliefs from size \(C\) subset of sampled observations

For each action

Reweight particles

Estimate Belief Value: \(V(\tau(b,a,z)) = w_{\tau(b,a,z)}^T\alpha\)

w(s')= \eta^{-1} w(s'_-)\mathcal{Z}(o|s_i',a)

Terminate Exploration

\(\text{depth}(b) > D\)

- maximum depth reached

 

OR

 

\(\text{WEU}(b) < 0\)

- exploration of belief node no longer heuristically promising

 

Finally, traverse each node back up to the root performing Bellman backups along the way

Phantom Observation

C_{b,a} \subseteq \text{support}(p(z|s,a)) \implies \neg \square \left(\sum_{z\in C_{b,a}}p(z|s_+,a) = 1\right)

\(C_{b,a}\) may not contain all possible observations

Q(b,a) = \sum_{s\in \Phi_b} w_b(s)R(s,a) + \frac{\gamma}{\eta}\sum_{z\in C_{b,a}}p(z|b,a)V(\tau(baz)) \\ \eta = \sum_{z\in C_{b,a}}p(z|b,a) \\
Q(b,a) = \sum_{s\in \Phi_b} w_b(s)R(s,a) + \gamma\sum_{z\in C_{b,a}}p(z|b,a)V(\tau(baz))
p(z|b,a) = \sum_{s' \in \Phi_{\tau(baz)}}w_b(s'_-)p(z|s',a) = \sum_{s' \in \Phi_{b}}w_b(s)p(z|s_+,a)

Claim:

\(\alpha\) now dependent on \(\eta\), which itself is dependent on \(w_b(s) \implies\) can't share \(\alpha\)'s between sibling nodes 

\alpha^a_{n+1,b} = R(s,a) + \gamma\sum_{z}p(z|s_+,a)\alpha_{n,\tau(baz)}(s_+)

Phantom Observation

Proposed Solution

  • Introduce some residual observation \((z_{res})\) that accounts for all observations not recovered in \(C_{b,a}\)
  • Normalize observation probabilities in a manner that shifts weights towards observations that were collected rather than \(z_{res}\)
\eta_{max} = \max_{s'}\sum_{z\in C_{b,a}\setminus z_{res}}p(z|s',a) \\ p(z|s',a) \leftarrow p(z|s',a)\eta^{-1}_{max}

Experiments

  • Tiger
    • Standard Tiger problem, but continuous \(\mathcal{O}\) and two listening actions (differing in reward and accuracy)
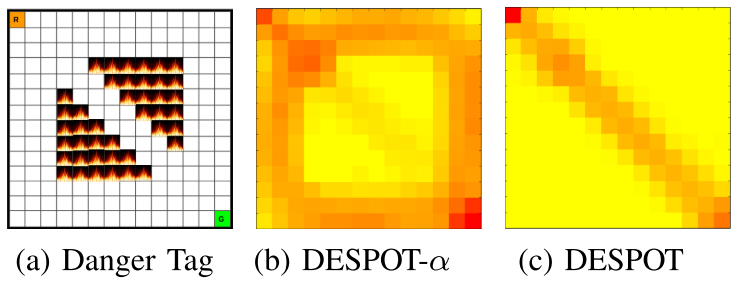
  • Danger Tag
    • Laser Tag, but requires localization and avoidance of dangerous areas
  • Rock Sample (RS)
    • Collect good rocks
    • given sensor to check each of \(n\) rocks for "goodness"
  • Multi-Agent Rock Sample (MARS)
    • Same as RS, but 2 agents (\(|\mathcal{A}|=\)225,400,625)
  • Navigation in Partially known map
    • Uncertainty about own position as well as position of certain obstacles in the map
  • Car Driving Among Pedestrians
    • Maneuver from start position to goal location without colliding with walking pedestrians with noisy dynamics

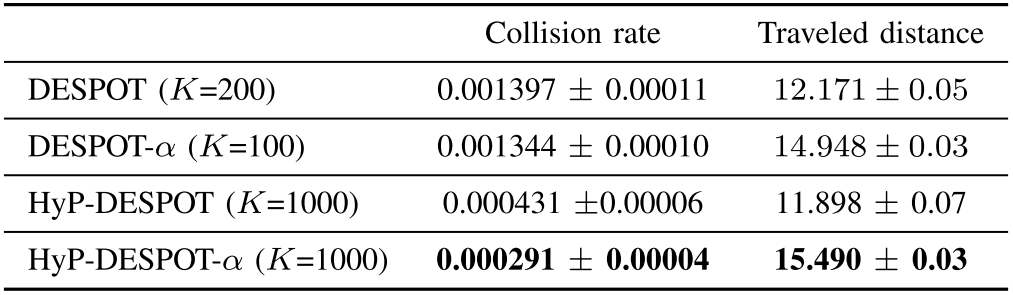
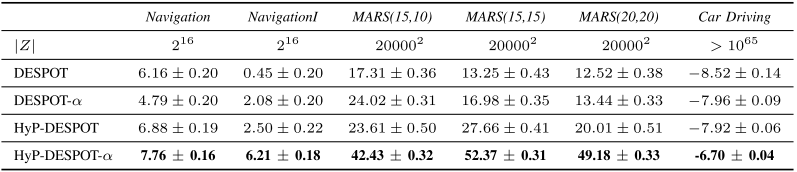
Computation

  • Planning Times
    • 0.1s for driving scenario, 1s otherwise
  • DESPOT/DESPOT-\(\alpha\) using only CPU, no parallelization
  • HyP-DESPOT/HyP-DESPOT-\(\alpha\) using both CPU and GPU with parallelization
    • CPU parallelizes tree traversal
    • GPU parallelizes rollouts + sibling node evaluation

Legacy

  • 11 citations
  • All connectedpapers listings only reference DESPOT-\(\alpha\) in background sections

Critiques

  • Insufficient justification of "phantom" observation (\(z_{res}\))
  • Exhaustive \(\mathcal{A}\) search 
    • Every scenario takes every action
  • Messy pseudocode
  • No comparison to other large \(\mathcal{O}\) algorithms

Contributions (Recap)

  • Extension of DESPOT to large observation spaces
  • Minimizing overhead of expansion to large observation spaces
    • Parallelizable leaf node evaluation with \(\alpha\)-vectors
  • Extension of Hyp-DESPOT to fully parallelized HyP-DESPOT-\(\alpha\)

DESPOT + Weighted PF + \(\alpha\) vectors

Made with Slides.com