Big O
The measurement of Algorithmic Complexity
Objectives
- Define Algorithmic Complexity
- Describe the relationship between "algorithmic complexity", Big O, and "runtime" of a program.
- Compute the Big O of an algorithm
Primer Questions
What is an algorithm?
Are all programs algorithms?
Primer Questions
What is the "runtime" of a program?
Primer Questions
How many operations will occur when I run this program?
var arr = [1, 2, 3, 4, 5];
var sum = 0;
while(i < arr.length) {
sum += arr.length;
i++;
}Primer Questions
2 + 3*5 = 17
var arr = [1, 2, 3, 4, 5];
var sum = 0;
while(i < arr.length) {
sum += arr.length;
i++;
}At its heart, computing Big O is about counting the number of operations a program will run.
Big O -- Medium Formality
"A theoretical measure of the execution of an algorithm. Usually the time or memory needed for the algorithm to complete given the problem size n.
Big O
"A theoretical measure of the execution of an algorithm. Usually the time or memory needed for the algorithm to complete given the problem size n.
Theoretical: We're dealing with the abstraction, not necessarily a specific implementation.
Big O
"A theoretical measure of the execution of an algorithm. Usually the time or memory needed for the algorithm to complete given the problem size n.
Time or Memory: We can measure two categories of complexity.
Time complexity is the number of operations a program must execute before completing
Big O
"A theoretical measure of the execution of an algorithm. Usually the time or memory needed for the algorithm to complete given the problem size n.
Time or Memory: We can measure two categories of complexity.
Memory complexity is the amount of data that must be stored before the algorithm completes.
Big O
"A theoretical measure of the execution of an algorithm. Usually the time or memory needed for the algorithm to complete given the problem size n.
Problem Size n: The algorithmic complexity is based on the size of the input.
Big O -- Informal
An estimate of the runtime or storage requirements of an algorithm
"Asymptotic Complexity"
The reason we measure algorithms in Big O is to determine how they behave as n gets very large.
In this way, Big O is kind of like limits in calculus. We care about the big o as n approaches infinity.
"Asymptotic Complexity"
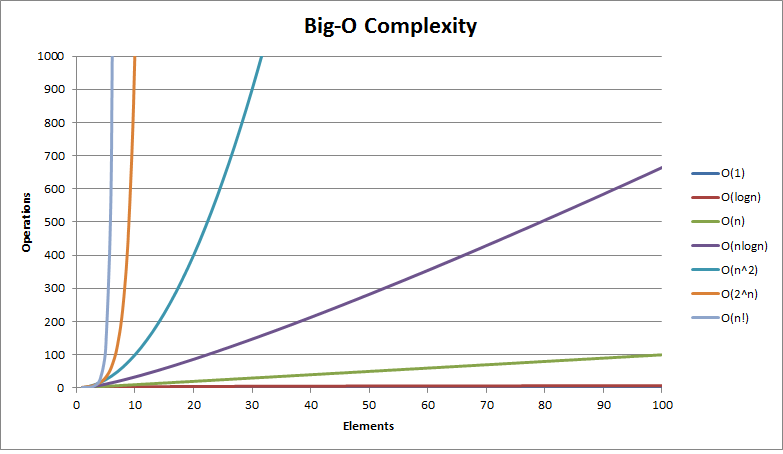
"Asymptotic Complexity"
With your table, discuss why computer scientists tend to only care about complexity as n gets large.
What are some potential drawbacks of this mentality?
"Asymptotic Complexity"
Consider this program:
function twoLoops(n) {
let sum = 0;
for(let i = 0; i < 100000000; i++) {
sum += 1
}
for(let i = 0; i < n; i++) {
sum += 1
}
}What is the time complexity Big O of this function?
function twoLoops(n) {
let sum = 0;
for(let i = 0; i < 100000000; i++) {
sum += 1
}
for(let i = 0; i < n; i++) {
sum += 1
}
}
Can you plot the line/curve for our twoLoops function on this graph?
Take A Break!
We are going to "learn by doing" and examine several programs to determine their big o values when you come back.
function print50nums() {
for (var i = 0; i < 50; i++) {
console.log(i);
}
}function print500000nums() {
for (var i = 0; i < 500000; i++) {
console.log(i);
}
}function addSomeNumbers(arr) {
sum = 0;
for (var i=0; i < arr.length; i++) {
sum += arr[i];
}
return sum;
}function printAllSubstrings(string) {
for(var i = 0; i < string.length; i++) {
for(var j = i; j < string.length; j++) {
console.log(string.substring(i, j));
}
}
}Binary Search (recursive)
function binarySearch(arr, lowIndex, highIndex, searchVal) {
var sliceLength = highIndex - lowIndex;
var midIndex = lowIndex + Math.floor(sliceLength / 2);
var midVal = arr[midIndex];
if(midVal === searchVal){
return midIndex;
}
else if(lowIndex === highIndex) {
return -1;
}
else if(searchVal < midVal) {
return binarySearch(arr, lowIndex, midIndex - 1, searchVal);
}
else if(searchVal > midVal) {
return binarySearch(arr, midIndex + 1, highIndex, searchVal);
}
else {
throw new Error("Incompatible data -- no comparison returned true");
}
throw new Error("Reached what should be unreachable code.");
}Binary Search (iterative)
function binaryIndexOf(searchElement) {
var minIndex = 0;
var maxIndex = this.length - 1;
var currentIndex;
var currentElement;
while (minIndex <= maxIndex) {
currentIndex = (minIndex + maxIndex) / 2 | 0;
currentElement = this[currentIndex];
if (currentElement < searchElement) {
minIndex = currentIndex + 1;
}
else if (currentElement > searchElement) {
maxIndex = currentIndex - 1;
}
else {
return currentIndex;
}
}
return -1;
}Iterative Fibonacci sequence
function fibbonacciIterative(n) {
if(n <= 1) {
return 1;
}
var fibNumber;
var numberOne = 1;
var numberTwo = 1;
for(var i = 1; i < n; i++) {
fibNumber = numberOne + numberTwo;
numberOne = numberTwo;
numberTwo = fibNumber;
}
return fibNumber;
}Recursive Fibonacci sequence
function fibbonacciRecursive(n) {
if(n <= 1) {
return 1;
}
return fibbonacciRecursive(n - 1) + fibbonacciRecursive(n - 2);
}Big O -- Formal
f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.
reading the notation:
"F of n is said to be Big Oh of g of n"
THIS DEFINITION IS PURELY ACADEMIC
No employer that isn't a university will EVER care if you can describe Big O in this level of detail.
That doesn't mean it isn't worth examining...
Big O -- Formal
f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.
This is full of "math-ese", which makes it a bit intimidating. Lets break it down with an example.
Big O -- Formal
f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.
This equation is a statement about a function called f. Lets call this function f:
function f(arr) {
var sum = 0;
while(i < arr.length) {
sum += arr.length;
i++;
}
}Big O -- Formal
f(n) = O(g(n))
function f(arr) {
var sum = 0;
while(i < arr.length) {
sum += arr.length;
i++;
}
}n represents the "size of the input".
f( [1, 2, 3, 4] ); // n === 4
f( [1, 2, 3, 4, 5] ); // n === 5
f( [1, 2, 3, 4, 6, 7, 8] ); // n === 8Big O -- Formal
f(n) = O(g(n))
Because the Big O notation is relative to the input size the Big O is a measure of how the algorithm scales.
function f(arr) {
var sum = 0;
while(i < arr.length) {
sum += arr.length;
i++;
}
}Big O -- Formal
f(n) = O(g(n))
An equation for the operations run by this algorithm:
Ops = 1 + 3*arr.length
Ops = 1 + 3n
f(n) = O(c1 + c2*n)
f(n) = O(n)
function f(arr) {
var sum = 0;
while(i < arr.length) {
sum += arr.length;
i++;
}
}Big O -- Formal
f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.
Ops = 1 + 3n
f(n) == O(c1 + c2*n) == O(n)
f(n) is said to be O(n)
g(n) is the stand in for our magnitude: n
As soon as n > 3, the size of n "dominates" the equation 1+3*n
Big O -- Formal
f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.
This "domination" is the core of Big O.
For every algorithm, there comes a point where the size of the input becomes more important than any other factor.
Big O -- Formal
f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.
Recall:
f(n) = 1 + 3n
so, it is true that 0 ≤ f(n) ≤ cg(n)
for all n ≥ 4
k == 4, c == 1
Big O -- Formal
f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.
Recall:
f(n) = 1 + 3n
Can we choose different values for c and k that still satisfy the question?
Big O -- Formal
f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.
Recall:
f(n) = 1 + 50n + 2n^2
What is the big O of this new formula?
What are valid some choices of c and k?