Ρευστά:

H εξίσωση του Bernoulli

Οι δυνάμεις

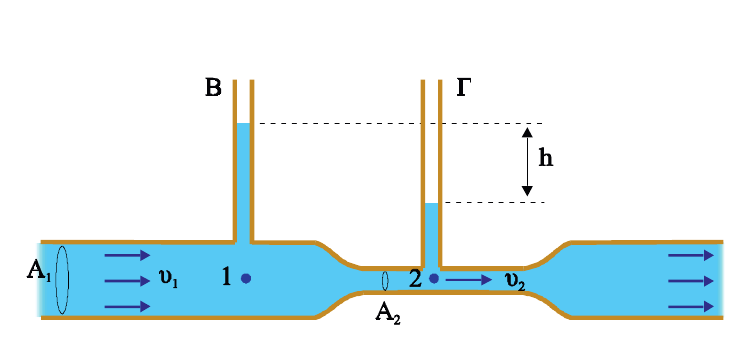
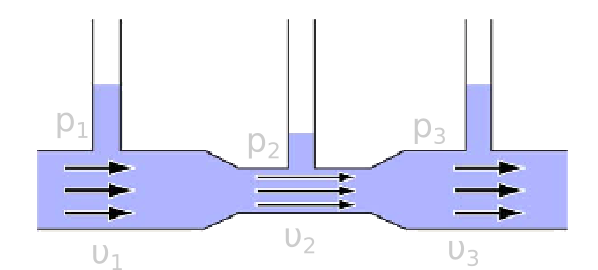
Στον σωλήνα του σχήματος υπάρχει ιδανικό υγρό...

  • Το ύψος του υγρού στα δύο σκέλη είναι ίδιο.
  • Η στοιχειώδης μάζα δέχεται και στις δύο πλευρές της ίσες κατά μέτρο δυνάμεις και δεν επιταχύνεται:

 

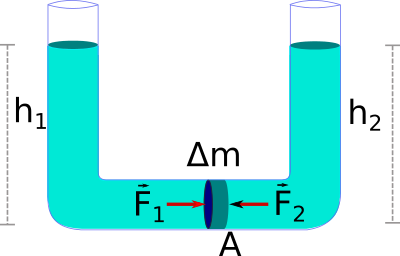
F_1 = p_1\cdot A
F1=p1⋅AF_1 = p_1\cdot A
F_2 = p_2\cdot A
F2=p2⋅AF_2 = p_2\cdot A
\color{Yellow}{F_{o \lambda}=(p_1-p_2)\cdot A =0}
Foλ=(p1−p2)⋅A=0\color{Yellow}{F_{o \lambda}=(p_1-p_2)\cdot A =0}

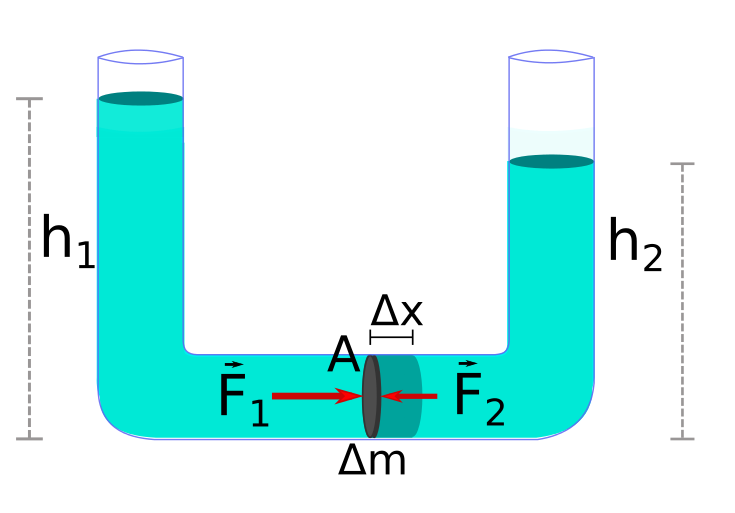
Αν οι πιέσεις μεταβληθούν, η στοιχειώδης μάζα μετακινείται κατά Δx και παράγεται έργο:

 

W = F_{o\lambda} \cdot \Delta x
W=Foλ⋅ΔxW = F_{o\lambda} \cdot \Delta x

ή

W = (p_1-p_2)A\cdot \Delta x\Rightarrow {\color{Yellow}{ W = (p_1-p_2)\cdot \Delta V}}
W=(p1−p2)A⋅Δx⇒W=(p1−p2)⋅ΔVW = (p_1-p_2)A\cdot \Delta x\Rightarrow {\color{Yellow}{ W = (p_1-p_2)\cdot \Delta V}}
\color {Yellow} {{W \over \Delta V} = \Delta p}
WΔV=Δp\color {Yellow} {{W \over \Delta V} = \Delta p}

Text

η επιπλέον πίεση δίνει

το έργο ανά μονάδα όγκου...

Γενικά:

Αν κατά μήκος μίας φλέβας (συνεχής ροή), μετακινείται μια στοιχειώδης μάζα, Δm

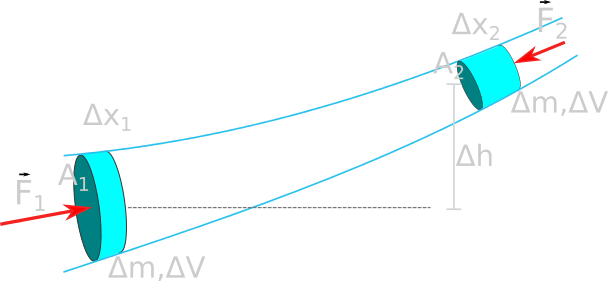
H ενέργεια που προσφέρεται ανά μονάδα όγκου, μετατρέπεται σε Κινητική και Δυναμική ενέργεια

(διατήρηση της ενέργειας)

W = \color{Red}{\Delta K} +\color{Aqua}{ \Delta U_\beta}
W=ΔK+ΔUβW = \color{Red}{\Delta K} +\color{Aqua}{ \Delta U_\beta}
(p_1-p_2)\cdot \Delta V = \color{Red}{\frac{1}{2}\cdot \Delta m\cdot (\upsilon^2_2 - \upsilon^2_1)}+\color{Aqua}{\Delta m\cdot g (h_2 - h_1)}
(p1−p2)⋅ΔV=12⋅Δm⋅(υ22−υ12)+Δm⋅g(h2−h1)(p_1-p_2)\cdot \Delta V = \color{Red}{\frac{1}{2}\cdot \Delta m\cdot (\upsilon^2_2 - \upsilon^2_1)}+\color{Aqua}{\Delta m\cdot g (h_2 - h_1)}

όπου η πυκνότητα

p_1 + \frac{1}{2}\cdot \varrho\cdot\upsilon^2_1+ \varrho\cdot g \cdot h_1 = p_2 + \frac{1}{2}\cdot \varrho\cdot\upsilon^2_2+ \varrho\cdot g \cdot h_2
p1+12⋅ϱ⋅υ12+ϱ⋅g⋅h1=p2+12⋅ϱ⋅υ22+ϱ⋅g⋅h2p_1 + \frac{1}{2}\cdot \varrho\cdot\upsilon^2_1+ \varrho\cdot g \cdot h_1 = p_2 + \frac{1}{2}\cdot \varrho\cdot\upsilon^2_2+ \varrho\cdot g \cdot h_2
\varrho =\frac{\Delta m}{\Delta V}
ϱ=ΔmΔV\varrho =\frac{\Delta m}{\Delta V}
\color{Yellow}{p + \frac{1}{2}\cdot \varrho\cdot\upsilon^2+ \varrho\cdot g \cdot h = \sigma \tau \alpha \vartheta.}
p+12⋅ϱ⋅υ2+ϱ⋅g⋅h=σταϑ.\color{Yellow}{p + \frac{1}{2}\cdot \varrho\cdot\upsilon^2+ \varrho\cdot g \cdot h = \sigma \tau \alpha \vartheta.}

Εξίσωση του Bernoulli

Παρατηρήσεις

Σύμφωνα με την εξίσωση του Βernoulli:

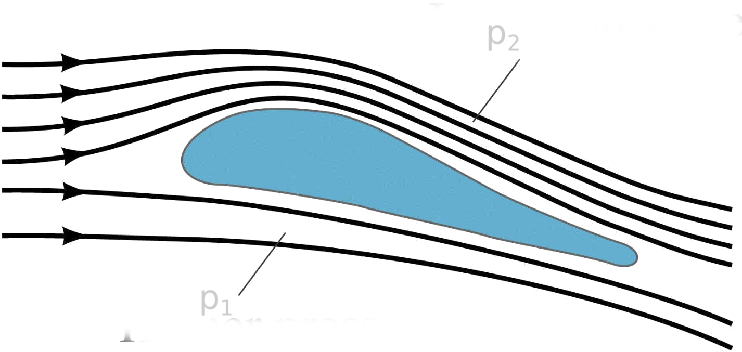
  • Σε περιοχές με αυξημένη ρευματική ταχύτητα (πυκνότερες ρευματικές γραμμές) η πίεση ελαττώνεται.

 

 

 

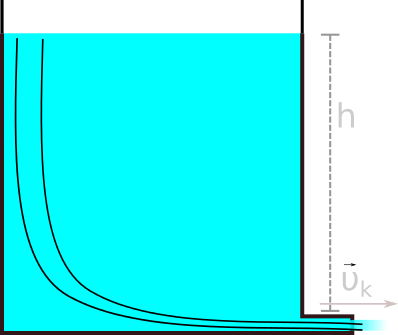
  • Η ταχύτητα εκροής του υγρού στο διπλανό δοχείο:

 

\upsilon _k = \sqrt{2gh}
υk=2gh\upsilon _k = \sqrt{2gh}
p_1>p_2
p1>p2p_1>p_2
Εφαρμογή:

 

Για την διάταξη του σχήματος, να δείξετε ότι η ταχύτητα ροής του (ιδανικού) υγρού στην περιοχή (1) δίνεται από τη σχέση :

\upsilon_1=\sqrt{\frac{2gh}{(\frac{A_1}{A_2})^2-1}}
υ1=2gh(A1A2)2−1\upsilon_1=\sqrt{\frac{2gh}{(\frac{A_1}{A_2})^2-1}}